人教版数学八年级上册13.4 课题学习 最短路径问题 同步练习(word解析版)
文档属性
| 名称 | 人教版数学八年级上册13.4 课题学习 最短路径问题 同步练习(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 611.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-29 14:01:15 | ||
图片预览

文档简介
13.4
课题学习
最短路径问题
一、单选题
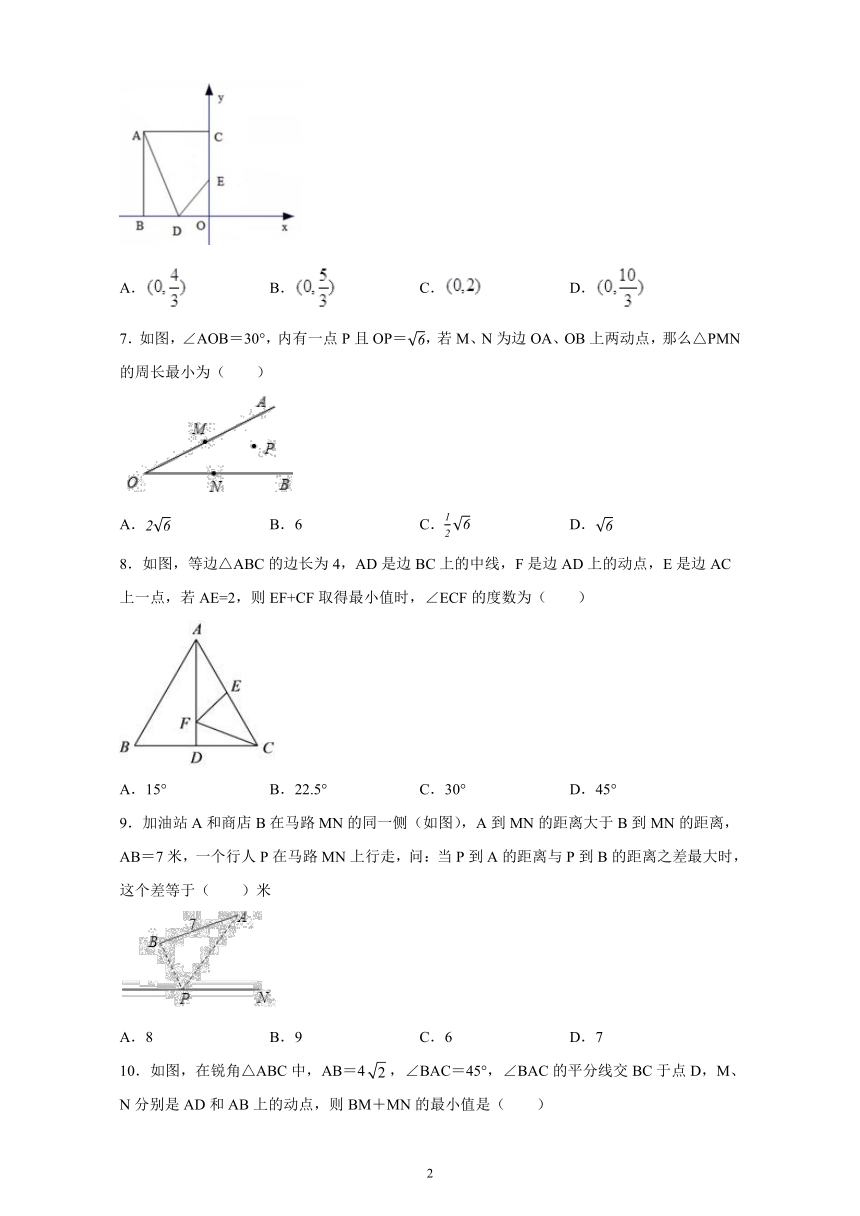
1.A,B,C三个车站在东西方向笔直的一条公路上,现要建一个加油站使其到三个车站的距离和最小,则加油站应建在( )
A.在A的左侧
B.在AB之间
C.在BC之间
D.B处
2.如图,点P是直线a外一点,PB⊥a,点A,B,C,D都在直线a上,下列线段中最短的是(
)
A.PA
B.PB
C.PC
D.PD
3.已知两点M(3,5),N(1,-1),点P是x轴上一动点,若使PM+PN最短,则点P的坐标应为(
)
A.(
,-4)
B.(
,0)
C.(
,0)
D.(
,0)
4.如图,牧童在A处放牛,其家在B处,A、B到河岸的距离分别为AC和BD,且AC=BD,若点A到河岸CD的中点的距离为500米,则牧童从A处把牛牵到河边饮水再回家,最短距离是( )
A.750米
B.1000米
C.1500米
D.2000米
5.如图所示,从点A到点F的最短路线是( )
A.A→D→E→F
B.A→C→E→F
C.A→B→E→F
D.无法确定
6.如图,矩形的顶点的坐标为,是的中点,是上的一点,当的周长最小时,点的坐标是(
)
A.
B.
C.
D.
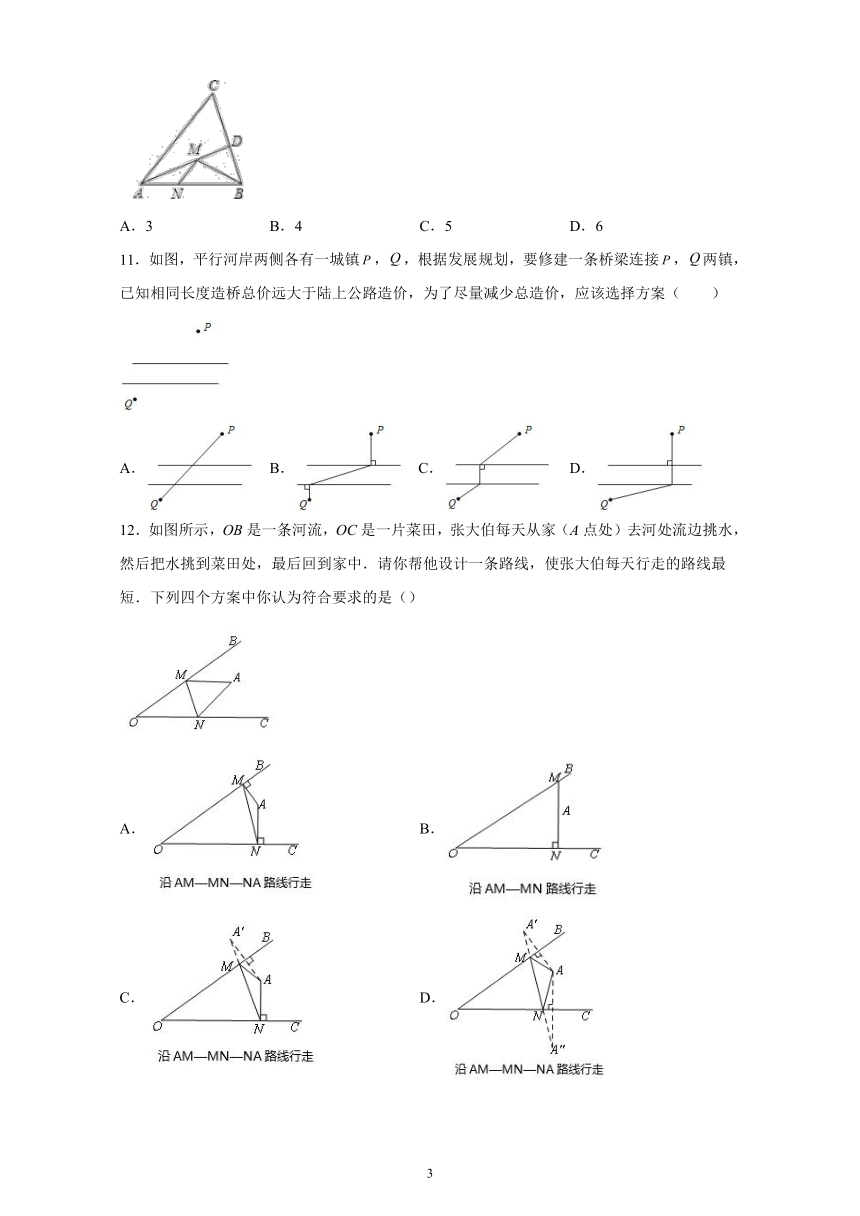
7.如图,∠AOB=30°,内有一点P且OP=,若M、N为边OA、OB上两动点,那么△PMN的周长最小为(
)
A.
B.6
C.
D.
8.如图,等边△ABC的边长为4,AD是边BC上的中线,F是边AD上的动点,E是边AC上一点,若AE=2,则EF+CF取得最小值时,∠ECF的度数为(
)
A.15°
B.22.5°
C.30°
D.45°
9.加油站A和商店B在马路MN的同一侧(如图),A到MN的距离大于B到MN的距离,AB=7米,一个行人P在马路MN上行走,问:当P到A的距离与P到B的距离之差最大时,这个差等于(
)米
A.8
B.9
C.6
D.7
10.如图,在锐角△ABC中,AB=4,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是(
)
A.3
B.4
C.5
D.6
11.如图,平行河岸两侧各有一城镇,,根据发展规划,要修建一条桥梁连接,两镇,已知相同长度造桥总价远大于陆上公路造价,为了尽量减少总造价,应该选择方案(
)
B.
C.
D.
12.如图所示,OB是一条河流,OC是一片菜田,张大伯每天从家(A点处)去河处流边挑水,然后把水挑到菜田处,最后回到家中.请你帮他设计一条路线,使张大伯每天行走的路线最短.下列四个方案中你认为符合要求的是()
A.
B.
C.
D.
二、填空题
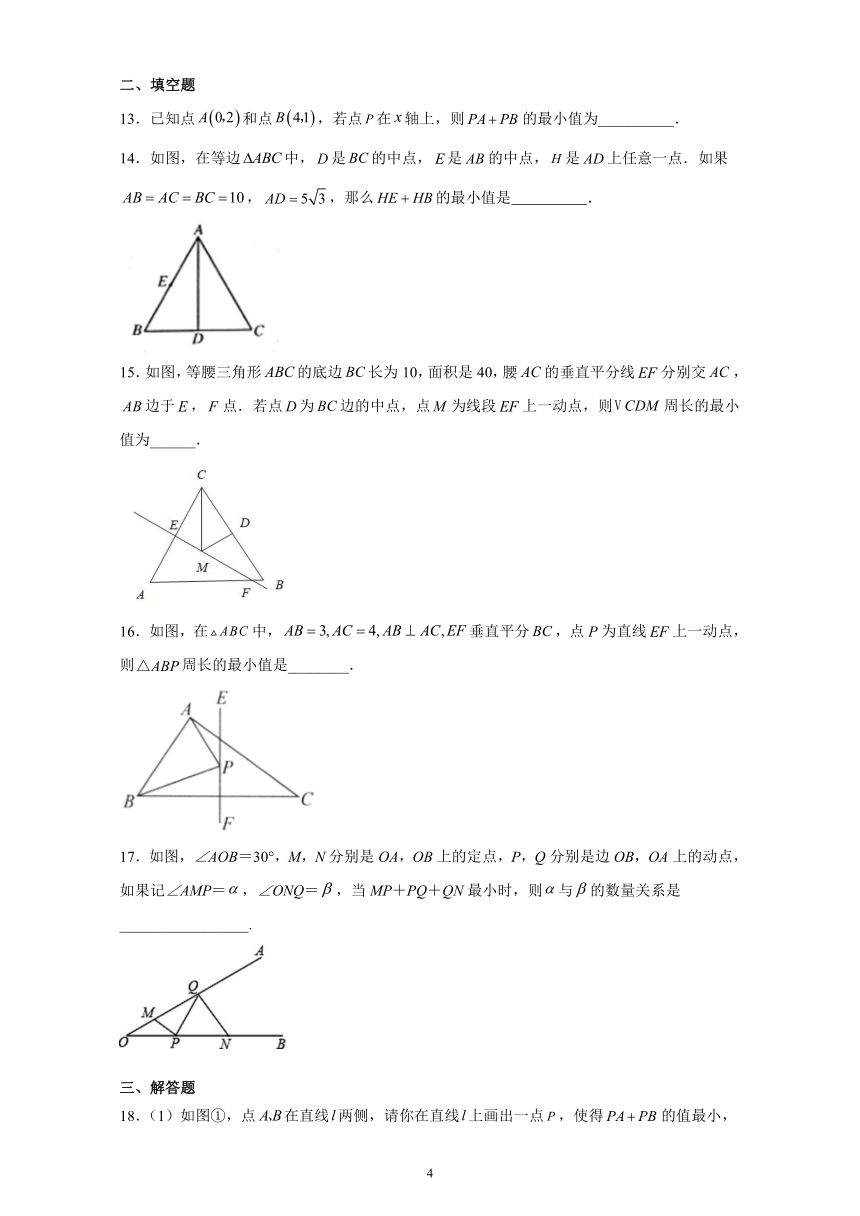
13.已知点和点,若点在轴上,则的最小值为__________.
14.如图,在等边中,是的中点,是的中点,是上任意一点.如果,,那么的最小值是
.
15.如图,等腰三角形的底边长为10,面积是40,腰的垂直平分线分别交,边于,点.若点为边的中点,点为线段上一动点,则周长的最小值为______.
16.如图,在中,垂直平分,点P为直线上一动点,则周长的最小值是________.
17.如图,∠AOB=30°,M,N分别是OA,OB上的定点,P,Q分别是边OB,OA上的动点,如果记∠AMP=,∠ONQ=,当MP+PQ+QN最小时,则与的数量关系是_________________.
三、解答题
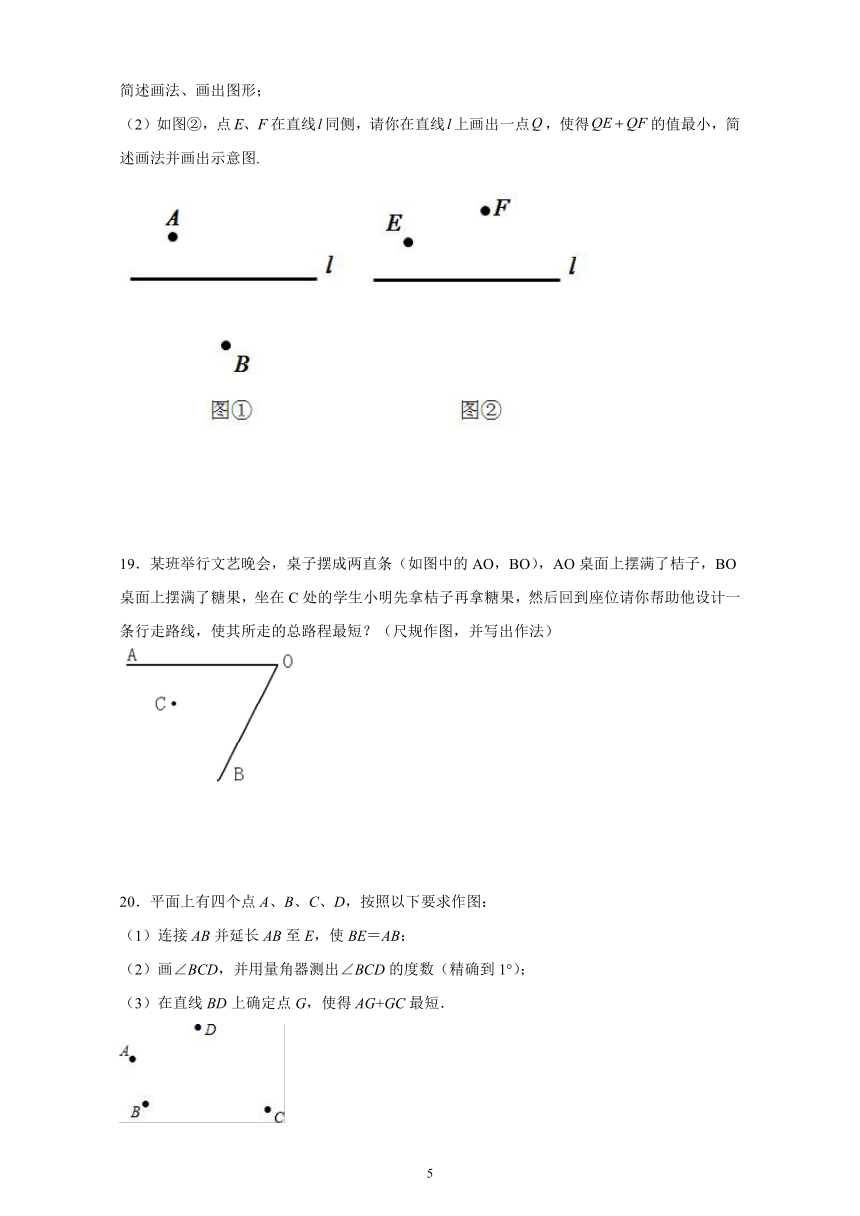
18.(1)如图①,点在直线两侧,请你在直线上画出一点,使得的值最小,简述画法、画出图形;
(2)如图②,点在直线同侧,请你在直线上画出一点,使得的值最小,简述画法并画出示意图.
19.某班举行文艺晚会,桌子摆成两直条(如图中的AO,BO),AO桌面上摆满了桔子,BO桌面上摆满了糖果,坐在C处的学生小明先拿桔子再拿糖果,然后回到座位请你帮助他设计一条行走路线,使其所走的总路程最短?(尺规作图,并写出作法)
20.平面上有四个点A、B、C、D,按照以下要求作图:
(1)连接AB并延长AB至E,使BE=AB;
(2)画∠BCD,并用量角器测出∠BCD的度数(精确到1°);
(3)在直线BD上确定点G,使得AG+GC最短.
21.如图,等边(三边相等,三个内角都是的三角形)的边长为,动点和动点同时出发,分别以每秒的速度由向和由向运动,其中一个动点到终点时,另一个也停止运动,设运动时间为,,和交于点.
(1)在运动过程中,与始终相等吗?请说明理由;
(2)连接,求为何值时,;
(3)若于点,点为上的点,且使最短.当时,的最小值为多少?请直接写出这个最小值,无需说明理由.
参考答案
1.D
解:设P、B的距离为xkm,
如图1:
路程之和为PA+PC+PB=(AC+x)km;
如图2:
路程之和为PA+PC+PB=(AC+x)km;
综上所述:路程之和为=(AC+x)km,
当x=0时,路程之和为AC的长度,则加油站应建在B处.
故选D
2.B
解:如图,PB是点P到a的垂线段,
∴线段中最短的是PB.
故选B.
3.C
解:如图,因为PM+PN最短,所以M,P,N三点共线,因为M(3,5),N(1,
-1),所以设解析式为把M(3,5),
N(1,
-1),分别代入解析式可得:
,解得,
其解析式为,
当y=0时,,
故P点坐标为(,0).
4.B
解:作A的对称点A’,连接A’B交CD于P,
,
,,
两点之间直线最短,A’B=AP+PB=1000米
5.C
解:由图中可以看出,从点A到点F,AB,EF是必须经过的路线,点B到点E的路线中BE最短,所以点A到点F的最短路线为A→B→E→F,
故答案选C.
6.B
解:如图,画出A点关于y轴的对称点A',连接A'D,与y轴交于点E,根据连接两点的连线中,线段最短,可知此时的周长最小,再由A,可得A'(4,5),因D(-2,0),即可求得直线DE表达式是,所以点的坐标是,故选B.
7.D
解:作P关于OA的对称点D,作P关于OB的对称点E,连接DE交OA于M,交OB于N,连接PM,PN,则此时△PMN的周长最小,此时周长最小值等于DE,
因为P,D关于OA对称,
所以OD=OP,
∠DOM=∠POM,
因为P,E关于OB对称,
所以OE=OP,
∠EON=∠PON,
因为∠DOE=∠DOM+∠POM+∠PON+∠EON=2∠MON,
∠AOB=30°,
所以∠DOE=2∠AOB=60°,
所以△DOE是等边三角形,
所以DE=OD=OP=,
所以△PMN的周长最小是,故选D.
8.C
解:过E作EM∥BC,交AD于N,
∵AC=4,AE=2,
∴EC=2=AE,
∴AM=BM=2,
∴AM=AE,
∵AD是BC边上的中线,△ABC是等边三角形,
∴AD⊥BC,
∵EM∥BC,
∴AD⊥EM,
∵AM=AE,
∴E和M关于AD对称,
连接CM交AD于F,连接EF,
则此时EF+CF的值最小,
∵△ABC是等边三角形,
∴∠ACB=60°,AC=BC,
∵AM=BM,
∴∠ECF=∠ACB=30°,
故选C.
9.D
解:当A,B,P三点不在同一直线上时,此时三点构成三角形,因为两边AP与BP的差小于第三边AB,所以A,B,P在同一直线上,所以P到A的距离与P到B的距离之差最大,这个差就是AB的长,故答案为:7.
10.B
解:如图,在AC上截取AE=AN,连接BE,
因为∠BAC的平分线交BC于点D,
所以∠EAM=∠NAM,
在△AME与△AMN中,,
所以△AME=△AMN,
所以ME=MN,
所以BM+MN=BM+ME≥BE,
因为BE是点B到直线AC的距离时,BE⊥AC,又AB=,
∠BAC=45°,此时,
△ABE为等腰直角三角形,所以BE=4,即BE取最小值为4,所以BM+MN的最小值是4,故选B.
11.C
解:如图,作PP'垂直于河岸L,使PP′等于河宽,连接QP′,与河岸L相交于N,作NM⊥L,则MN∥PP′且MN=PP′,于是四边形PMNP′为平行四边形,故PM=NP′.根据“两点之间线段最短”,QP′最短,即PM+NQ最短.观察选项,选项C符合题意.
故选C.
12.D
解:要找一条最短路线,以河流为轴,取A点的对称点A',连接A'N与河流相交于M点,再连接AM,则张大伯可沿着AM走一条直线去河边M点挑水,然后再沿MN走一条直线到菜园去,同理,画出回家的路线图如下:
故选D.
13.5
解:作点A关于x轴的对称点A′,连接A′B交x轴于点P,则P即为所求点;
∵点A(0,2),
∴点A关于x轴的对称点A′的坐标为(0,-2),
∵A′(0,-2),B(4,1),
∴A′B==5.
即PA+PB的最小值为5.
故答案为5.
14.
解:∵△ABC是等边三角形,
∴B点关于AD的对称点就是C点,
连接CE交AD于点H,此时HE+HB的值最小.
∴CH=BH,
∴HE+HB=CE,
根据等边三角形的性质,可知三条高的长度都相等,
∴CE=AD=.
故答案为:
.
15.13
解:连接AD,AM.
∵△ABC是等腰三角形,点D是BC边的中点,
∴AD⊥BC,
∴
,
解得AD=8,
∵EF是线段AC的垂直平分线,
∴点C关于直线EF的对称点为点A,
∴MA=MC,
∵
∴AD的长为的最小值,
∴△CDM的周长最短=.
故答案为:13.
16.7
解:∵垂直平分,
∴B,C关于直线对称.设交于点D,
∴当P和D重合时,的值最小,最小值等于的长,
∴周长的最小值是.
17.α-β=90°
解:如图,作M关于OB的对称点M′,N关于OA的对称点N′,连接M′N′交OA于Q,交OB于P,则MP+PQ+QN最小,
易知∠OPM=∠OPM′=∠NPQ,∠OQP=∠AQN′=∠AQN,
∵∠OQN=180°-30°-∠ONQ,∠OPM=∠NPQ=30°+∠OQP,
∠OQP=∠AQN=30°+∠ONQ,
∴.
∵,
∴
故答案为:.
18.(1)答案见详解;(2)答案见详解.
解:(1)如图①,连接AB,交直线l于点P,即为所求;
(2)如图②,作点E关于直线l的对称点E′,连接FE′,交直线l于点Q,即为所求.
19.见详解
解:如图.
作法:
(1)作点C关于OA的对称点A′,
(2)作点C关于OB的对称点B′,
(3)连接A′B′,分别于OA、OB相交于点D、点E,
(4)连接CD、CE,
则C→D→E→C就是小明所走的最短路线.
20.(1)图见解析;(2)∠BCD=45°;(3)图见解析.
解:(1)如图,线段BE即为所求;
(2)如图,连接CD并延长CD,连接CB并延长CB,∠BCD即为所求的角,∠BCD=45°;
(3)如图,当AGC三点共线时AG+GC最短,所以连接AC交BD于G,交点G即为所求点.
21.(1)CD与BE始终相等;(2)5;(3)7
解:(1)由已知可得AD=t,EC=t,
∴AD=CE,
∵△ABC是等边三角形
∴∠A=∠ACB=60°,BC=AC,
∴△ADC≌△CEB(SAS),
∴BE=CD,
∴CD与BE始终相等;
(2)∵DE∥BC,
∴AD=AE,
∵AB=AC=10,
∴t=10-t,
∴t=5;
(3)∵BM⊥AC,
∴BM平分∠ABC,
作D点关于BM的对称点D'交BC于点D',连接D'E,交BM于点P,
∵DP=D'P,
∴DP+PE=D'P+PE=D'E,
∵t=7,
∴AE=BD=BD′=3,AD=CE=7,
∴CD′=7,又∠C=60°,
∴△CD′E为等边三角形,
∴D'E=CD′=7,
∴PD+PE的最小值为7.
课题学习
最短路径问题
一、单选题
1.A,B,C三个车站在东西方向笔直的一条公路上,现要建一个加油站使其到三个车站的距离和最小,则加油站应建在( )
A.在A的左侧
B.在AB之间
C.在BC之间
D.B处
2.如图,点P是直线a外一点,PB⊥a,点A,B,C,D都在直线a上,下列线段中最短的是(
)
A.PA
B.PB
C.PC
D.PD
3.已知两点M(3,5),N(1,-1),点P是x轴上一动点,若使PM+PN最短,则点P的坐标应为(
)
A.(
,-4)
B.(
,0)
C.(
,0)
D.(
,0)
4.如图,牧童在A处放牛,其家在B处,A、B到河岸的距离分别为AC和BD,且AC=BD,若点A到河岸CD的中点的距离为500米,则牧童从A处把牛牵到河边饮水再回家,最短距离是( )
A.750米
B.1000米
C.1500米
D.2000米
5.如图所示,从点A到点F的最短路线是( )
A.A→D→E→F
B.A→C→E→F
C.A→B→E→F
D.无法确定
6.如图,矩形的顶点的坐标为,是的中点,是上的一点,当的周长最小时,点的坐标是(
)
A.
B.
C.
D.
7.如图,∠AOB=30°,内有一点P且OP=,若M、N为边OA、OB上两动点,那么△PMN的周长最小为(
)
A.
B.6
C.
D.
8.如图,等边△ABC的边长为4,AD是边BC上的中线,F是边AD上的动点,E是边AC上一点,若AE=2,则EF+CF取得最小值时,∠ECF的度数为(
)
A.15°
B.22.5°
C.30°
D.45°
9.加油站A和商店B在马路MN的同一侧(如图),A到MN的距离大于B到MN的距离,AB=7米,一个行人P在马路MN上行走,问:当P到A的距离与P到B的距离之差最大时,这个差等于(
)米
A.8
B.9
C.6
D.7
10.如图,在锐角△ABC中,AB=4,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是(
)
A.3
B.4
C.5
D.6
11.如图,平行河岸两侧各有一城镇,,根据发展规划,要修建一条桥梁连接,两镇,已知相同长度造桥总价远大于陆上公路造价,为了尽量减少总造价,应该选择方案(
)
B.
C.
D.
12.如图所示,OB是一条河流,OC是一片菜田,张大伯每天从家(A点处)去河处流边挑水,然后把水挑到菜田处,最后回到家中.请你帮他设计一条路线,使张大伯每天行走的路线最短.下列四个方案中你认为符合要求的是()
A.
B.
C.
D.
二、填空题
13.已知点和点,若点在轴上,则的最小值为__________.
14.如图,在等边中,是的中点,是的中点,是上任意一点.如果,,那么的最小值是
.
15.如图,等腰三角形的底边长为10,面积是40,腰的垂直平分线分别交,边于,点.若点为边的中点,点为线段上一动点,则周长的最小值为______.
16.如图,在中,垂直平分,点P为直线上一动点,则周长的最小值是________.
17.如图,∠AOB=30°,M,N分别是OA,OB上的定点,P,Q分别是边OB,OA上的动点,如果记∠AMP=,∠ONQ=,当MP+PQ+QN最小时,则与的数量关系是_________________.
三、解答题
18.(1)如图①,点在直线两侧,请你在直线上画出一点,使得的值最小,简述画法、画出图形;
(2)如图②,点在直线同侧,请你在直线上画出一点,使得的值最小,简述画法并画出示意图.
19.某班举行文艺晚会,桌子摆成两直条(如图中的AO,BO),AO桌面上摆满了桔子,BO桌面上摆满了糖果,坐在C处的学生小明先拿桔子再拿糖果,然后回到座位请你帮助他设计一条行走路线,使其所走的总路程最短?(尺规作图,并写出作法)
20.平面上有四个点A、B、C、D,按照以下要求作图:
(1)连接AB并延长AB至E,使BE=AB;
(2)画∠BCD,并用量角器测出∠BCD的度数(精确到1°);
(3)在直线BD上确定点G,使得AG+GC最短.
21.如图,等边(三边相等,三个内角都是的三角形)的边长为,动点和动点同时出发,分别以每秒的速度由向和由向运动,其中一个动点到终点时,另一个也停止运动,设运动时间为,,和交于点.
(1)在运动过程中,与始终相等吗?请说明理由;
(2)连接,求为何值时,;
(3)若于点,点为上的点,且使最短.当时,的最小值为多少?请直接写出这个最小值,无需说明理由.
参考答案
1.D
解:设P、B的距离为xkm,
如图1:
路程之和为PA+PC+PB=(AC+x)km;
如图2:
路程之和为PA+PC+PB=(AC+x)km;
综上所述:路程之和为=(AC+x)km,
当x=0时,路程之和为AC的长度,则加油站应建在B处.
故选D
2.B
解:如图,PB是点P到a的垂线段,
∴线段中最短的是PB.
故选B.
3.C
解:如图,因为PM+PN最短,所以M,P,N三点共线,因为M(3,5),N(1,
-1),所以设解析式为把M(3,5),
N(1,
-1),分别代入解析式可得:
,解得,
其解析式为,
当y=0时,,
故P点坐标为(,0).
4.B
解:作A的对称点A’,连接A’B交CD于P,
,
,,
两点之间直线最短,A’B=AP+PB=1000米
5.C
解:由图中可以看出,从点A到点F,AB,EF是必须经过的路线,点B到点E的路线中BE最短,所以点A到点F的最短路线为A→B→E→F,
故答案选C.
6.B
解:如图,画出A点关于y轴的对称点A',连接A'D,与y轴交于点E,根据连接两点的连线中,线段最短,可知此时的周长最小,再由A,可得A'(4,5),因D(-2,0),即可求得直线DE表达式是,所以点的坐标是,故选B.
7.D
解:作P关于OA的对称点D,作P关于OB的对称点E,连接DE交OA于M,交OB于N,连接PM,PN,则此时△PMN的周长最小,此时周长最小值等于DE,
因为P,D关于OA对称,
所以OD=OP,
∠DOM=∠POM,
因为P,E关于OB对称,
所以OE=OP,
∠EON=∠PON,
因为∠DOE=∠DOM+∠POM+∠PON+∠EON=2∠MON,
∠AOB=30°,
所以∠DOE=2∠AOB=60°,
所以△DOE是等边三角形,
所以DE=OD=OP=,
所以△PMN的周长最小是,故选D.
8.C
解:过E作EM∥BC,交AD于N,
∵AC=4,AE=2,
∴EC=2=AE,
∴AM=BM=2,
∴AM=AE,
∵AD是BC边上的中线,△ABC是等边三角形,
∴AD⊥BC,
∵EM∥BC,
∴AD⊥EM,
∵AM=AE,
∴E和M关于AD对称,
连接CM交AD于F,连接EF,
则此时EF+CF的值最小,
∵△ABC是等边三角形,
∴∠ACB=60°,AC=BC,
∵AM=BM,
∴∠ECF=∠ACB=30°,
故选C.
9.D
解:当A,B,P三点不在同一直线上时,此时三点构成三角形,因为两边AP与BP的差小于第三边AB,所以A,B,P在同一直线上,所以P到A的距离与P到B的距离之差最大,这个差就是AB的长,故答案为:7.
10.B
解:如图,在AC上截取AE=AN,连接BE,
因为∠BAC的平分线交BC于点D,
所以∠EAM=∠NAM,
在△AME与△AMN中,,
所以△AME=△AMN,
所以ME=MN,
所以BM+MN=BM+ME≥BE,
因为BE是点B到直线AC的距离时,BE⊥AC,又AB=,
∠BAC=45°,此时,
△ABE为等腰直角三角形,所以BE=4,即BE取最小值为4,所以BM+MN的最小值是4,故选B.
11.C
解:如图,作PP'垂直于河岸L,使PP′等于河宽,连接QP′,与河岸L相交于N,作NM⊥L,则MN∥PP′且MN=PP′,于是四边形PMNP′为平行四边形,故PM=NP′.根据“两点之间线段最短”,QP′最短,即PM+NQ最短.观察选项,选项C符合题意.
故选C.
12.D
解:要找一条最短路线,以河流为轴,取A点的对称点A',连接A'N与河流相交于M点,再连接AM,则张大伯可沿着AM走一条直线去河边M点挑水,然后再沿MN走一条直线到菜园去,同理,画出回家的路线图如下:
故选D.
13.5
解:作点A关于x轴的对称点A′,连接A′B交x轴于点P,则P即为所求点;
∵点A(0,2),
∴点A关于x轴的对称点A′的坐标为(0,-2),
∵A′(0,-2),B(4,1),
∴A′B==5.
即PA+PB的最小值为5.
故答案为5.
14.
解:∵△ABC是等边三角形,
∴B点关于AD的对称点就是C点,
连接CE交AD于点H,此时HE+HB的值最小.
∴CH=BH,
∴HE+HB=CE,
根据等边三角形的性质,可知三条高的长度都相等,
∴CE=AD=.
故答案为:
.
15.13
解:连接AD,AM.
∵△ABC是等腰三角形,点D是BC边的中点,
∴AD⊥BC,
∴
,
解得AD=8,
∵EF是线段AC的垂直平分线,
∴点C关于直线EF的对称点为点A,
∴MA=MC,
∵
∴AD的长为的最小值,
∴△CDM的周长最短=.
故答案为:13.
16.7
解:∵垂直平分,
∴B,C关于直线对称.设交于点D,
∴当P和D重合时,的值最小,最小值等于的长,
∴周长的最小值是.
17.α-β=90°
解:如图,作M关于OB的对称点M′,N关于OA的对称点N′,连接M′N′交OA于Q,交OB于P,则MP+PQ+QN最小,
易知∠OPM=∠OPM′=∠NPQ,∠OQP=∠AQN′=∠AQN,
∵∠OQN=180°-30°-∠ONQ,∠OPM=∠NPQ=30°+∠OQP,
∠OQP=∠AQN=30°+∠ONQ,
∴.
∵,
∴
故答案为:.
18.(1)答案见详解;(2)答案见详解.
解:(1)如图①,连接AB,交直线l于点P,即为所求;
(2)如图②,作点E关于直线l的对称点E′,连接FE′,交直线l于点Q,即为所求.
19.见详解
解:如图.
作法:
(1)作点C关于OA的对称点A′,
(2)作点C关于OB的对称点B′,
(3)连接A′B′,分别于OA、OB相交于点D、点E,
(4)连接CD、CE,
则C→D→E→C就是小明所走的最短路线.
20.(1)图见解析;(2)∠BCD=45°;(3)图见解析.
解:(1)如图,线段BE即为所求;
(2)如图,连接CD并延长CD,连接CB并延长CB,∠BCD即为所求的角,∠BCD=45°;
(3)如图,当AGC三点共线时AG+GC最短,所以连接AC交BD于G,交点G即为所求点.
21.(1)CD与BE始终相等;(2)5;(3)7
解:(1)由已知可得AD=t,EC=t,
∴AD=CE,
∵△ABC是等边三角形
∴∠A=∠ACB=60°,BC=AC,
∴△ADC≌△CEB(SAS),
∴BE=CD,
∴CD与BE始终相等;
(2)∵DE∥BC,
∴AD=AE,
∵AB=AC=10,
∴t=10-t,
∴t=5;
(3)∵BM⊥AC,
∴BM平分∠ABC,
作D点关于BM的对称点D'交BC于点D',连接D'E,交BM于点P,
∵DP=D'P,
∴DP+PE=D'P+PE=D'E,
∵t=7,
∴AE=BD=BD′=3,AD=CE=7,
∴CD′=7,又∠C=60°,
∴△CD′E为等边三角形,
∴D'E=CD′=7,
∴PD+PE的最小值为7.
