3.1.2函数的表示法课件-2020-2021学年高一上学期数学人教A版(2019)必修第一册(共30张PPT)
文档属性
| 名称 | 3.1.2函数的表示法课件-2020-2021学年高一上学期数学人教A版(2019)必修第一册(共30张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-28 22:09:13 | ||
图片预览








文档简介
(共30张PPT)
函数的表示法
安徽淮南第四中学
2020.10
新课程标准
核心素养
1.了解函数的三种表示法及各自的优缺点.
数学抽象
2.尝试作图并从图象上获取有用的信息.
直观想象
3.会用解析法及图象法表示分段函数.
数学建模
4.掌握求函数解析式的常见方法.
数学运算
5.能根据给出的分段函数,研究有关性质.
数据分析
【学法解读】
1.函数的三种表示方法体现了“式”“表”“图”的不同形态,特别是“式”与“图”的结合,体现了数形结合思想,学习过程中,应注意把它们相互结合,特别要注意加强“式”与“图”的相互转化,学生应从不同的侧面认识函数的本质.
2.学习分段函数时,学生要注意结合实例体会概念,还要注意书写的规范.
回顾
初中学过哪几种表示函数的方法?
表示函数的方法,常用的有解析法、列表法和图象法三种.
⑴解析法:就是用数学表达式表示两个变量之间的对应关系.
如,s=60t2,A=r2,S=2,y=ax2+bx+c(a≠0),y=x+2等等都是用解析式表示函数关系的.
(2)图象法:就是用图象表示两个变量之间的对应关系.
(3)列表法:就是列出表格来表示两个变量之间的对应关系.
例1
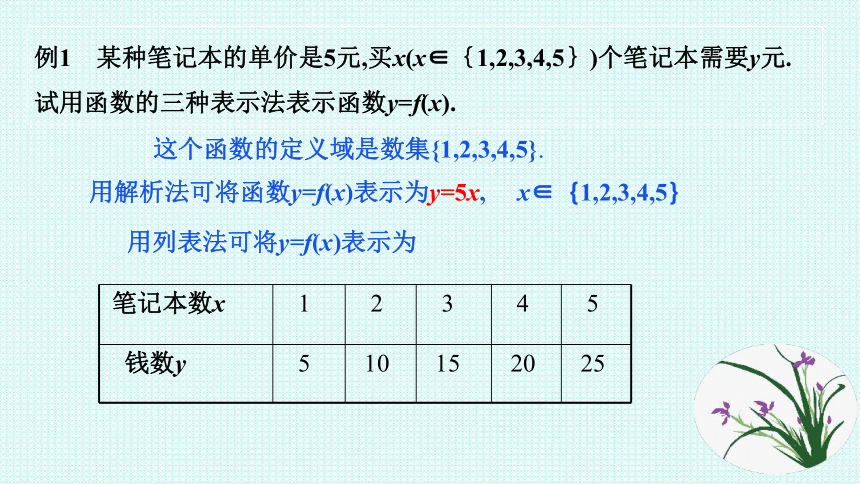
某种笔记本的单价是5元,买x(x∈{1,2,3,4,5})个笔记本需要y元.试用函数的三种表示法表示函数y=f(x).
这个函数的定义域是数集{1,2,3,4,5}.
用解析法可将函数y=f(x)表示为y=5x,
x∈{1,2,3,4,5}
用列表法可将y=f(x)表示为
笔记本数x
1
2
3
4
5
钱数y
5
10
15
20
25
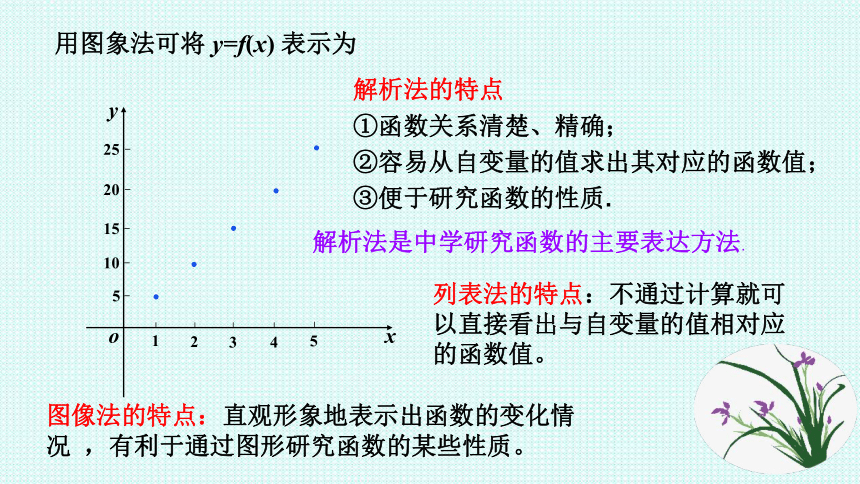
用图象法可将
y=f(x)
表示为
x
y
o
1
2
3
4
5
5
10
15
20
25
·
·
·
·
·
列表法的特点:不通过计算就可以直接看出与自变量的值相对应的函数值。
图像法的特点:直观形象地表示出函数的变化情况
,有利于通过图形研究函数的某些性质。
解析法的特点
①函数关系清楚、精确;
②容易从自变量的值求出其对应的函数值;③便于研究函数的性质.
解析法是中学研究函数的主要表达方法.
所有的函数都能用解析法表示吗?
不是所有的函数都能用解析法表示.
例如,某天24整点的整点数与这一刻的气温的关系.
题型一
与函数图象有关的问题
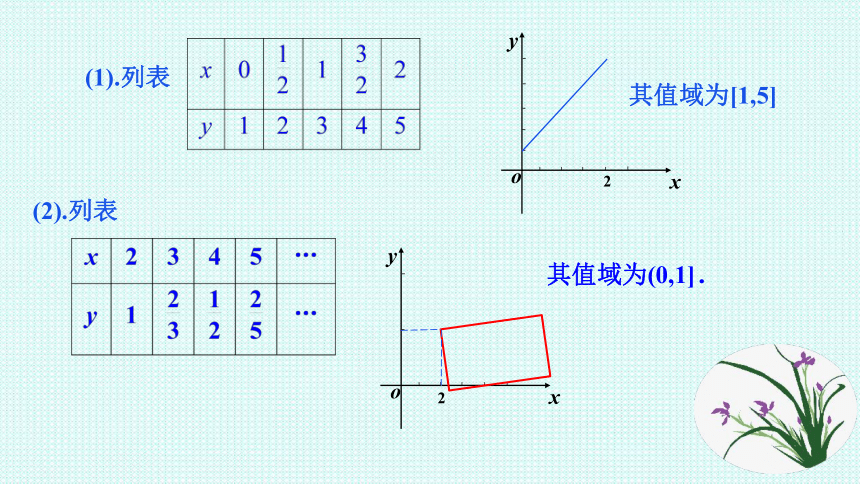
(1).列表
x
y
o
2
其值域为[1,5]
x
y
o
2
其值域为(0,1].
(2).列表
x
-2
-1
0
1
2
y
0
-1
0
3
8
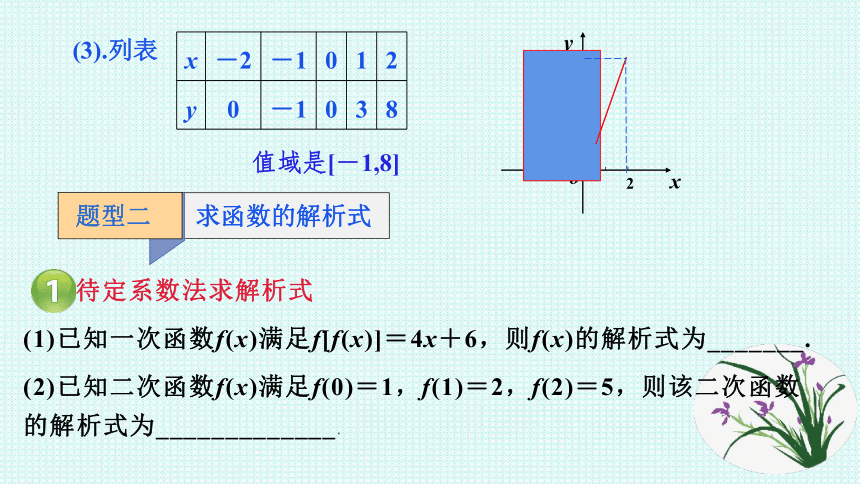
(3).列表
x
y
o
2
值域是[-1,8]
题型二
求函数的解析式
待定系数法求解析式
(1)已知一次函数f(x)满足f[f(x)]=4x+6,则f(x)的解析式为_______.
(2)已知二次函数f(x)满足f(0)=1,f(1)=2,f(2)=5,则该二次函数的解析式为_____________.
[解析] (1)设f(x)=ax+b(a≠0),
则f[f(x)]=f(ax+b)=a(ax+b)+b=a2x+ab+b=4x+6,
含参数a、b
比较系数
所以f(x)=2x+2或f(x)=-2x-6.
(2)设二次函数的解析式为f(x)=ax2+bx+c(a≠0),
换元法(或配凑法)求解析式
方程组法求函数解析式
分段函数
【题】画出函数y=|x|的图像
【解】由绝对值的概念,有y=
-x,x<0,
x,x≥0.
x
y
o
如果函数在定义域的不同的范围内,有着不同的对应关系,
则称这样的函数为分段函数.
分段函数的定义域是各段定义域的并集,值域是各段值域的并集.
题型一
分段函数的求值问题
[解析](1)f(-4)=-4+2=-2,
f(3)=2×3=6,f(-2)=-2+2=0,
f[f(-2)]=f(0)=02=0.
当a≥2时,2a=10,
可得a=5,符合题意;
[解析] f(5)=f[f(10)],f(10)=f[f(15)]=f(18)=21,
f(5)=f(21)=24.
题型二
分段函数的图像及应用
x
y
o
2
-2
°
f(x)在(-2,2]上的值域为[1,3).
x
y
o
2
1
题型三
分段函数的应用问题
例3.如图,在边长为4的正方形ABCD的边上有一点P,沿折线BCDA由点B(起点)向点A(终点)运动,设点P运动的路程为x,△APB的面积为y.
(1)求y关于x的函数关系式y=f(x);
(2)画出y=f(x)的图象;
(3)若△APB的面积不小于2,求x的取值范围.
A
B
C
D
?
?
P
x
?
?
P
P
x
y
o
2
4
6
8
10
12
2
4
6
8
例3
某市“招手即停”公共汽车的票价按下列规则制定:
(1)5公里以内(含5公里),票价2元;
(2)5公里以上,每增加5公里,票价增加1元(不足5公里的按5公里计算)
如果某条线路的总里程为20公里,请根据题意,
写出票价与里程之间的函数解析式,并画出函数的图象.
y=
2,
0≤
5
3,
5
<
x
≤
10
4,
10
<
x
≤
15
5,
15
<
x≤20
○
2
O
5
10
15
20
1
3
4
5
x
○
○
○
2.某质点在30s内运动速度vcm/s是时间t的函数,它的图象如右图,用解析式表示出这个函数.
30
t/s
10
20
10
30
v/cm·s-1
O
15
20
25
5
解:v(t)=
t+10,
0
≤
t<5,
3t,
5
≤
t<10,
30,
10
≤t
<20,
-3t+90,
20
≤
t≤30.
【对点练习】?
某市有A,B两家羽毛球俱乐部,两家设备和服务都很好,但收费方式不同,A俱乐部每块场地每小时收费6元;B俱乐部按月计费,一个月中20小时以内(含20小时)每块场地收费90元,超过20小时的部分,每块场地每小时2元,某企业准备下个月从这两家俱乐部中的一家租用一块场地开展活动,其活动时间不少于12小时,也不超过30小时.
(1)设在A俱乐部租一块场地开展活动x小时的收费为f(x)元(12≤x≤30),在B俱乐部租一块场地开展活动x小时的收费为g(x)元(12≤x≤30),试求f(x)与g(x)的解析式;
(2)问该企业选择哪家俱乐部比较合算,为什么?
某同学骑车上学,离开家不久,发现作业本忘家里了,于是返回家找到作业再去上学,为了赶时间他快速行驶,如图中横轴表示出发后的时间,纵轴表示离学校的距离.则较符合该同学走法的图像是( )
d0
d0
d0
d0
t0
t0
t0
t0
x
y
o
x
y
o
x
y
o
x
y
o
A
B
C
D
例4.给定函数f(x)=x+1,
g(x)=(x+1)2,
x∈R
(1)
在同一直角坐标系中画出函数
f(x),
g(x)
的图象;
(2)
用M(x)表示
f(x),
g(x)
中的较大者,记为
试分别用图象法和解析法表示函数M(x).
x
y
o
x
y
o
2.函数y=|x+1|的图象是( )
x
y
o
x
y
o
x
y
o
x
y
o
解:(1)∵f(-2)=1-2×(-2)=5,
∴f(f(-2))=f(5)=4-52=-21.
(2)当a∈R时,a2+1≥1>0,∴f(a2+1)=4-(a2+1)2=-a4-2a2+3(a∈R).
(3)①当-4≤x<0时,f(x)=1-2x,∴1<f(x)≤9;
②当x=0时,f(x)=2;
③当0<x<3时,f(x)=4-x2,
∴-5<f(x)<4.
故当-4≤x<3时,函数f(x)的值域是(-5,9].
4.如图所示,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4).
(1)求f(f(0))的值;
(2)求函数f(x)的解析式.
B
1
3
o
x
y
A
C
2
4
1
2
3
4
5
6
[解](1)直接由图中观察,可得f(f(0))=f(4)=2.
(2)设线段AB所对应的函数解析式为y=kx+b,
∴y=-2x+4(0≤x≤2).
函数的表示法
安徽淮南第四中学
2020.10
新课程标准
核心素养
1.了解函数的三种表示法及各自的优缺点.
数学抽象
2.尝试作图并从图象上获取有用的信息.
直观想象
3.会用解析法及图象法表示分段函数.
数学建模
4.掌握求函数解析式的常见方法.
数学运算
5.能根据给出的分段函数,研究有关性质.
数据分析
【学法解读】
1.函数的三种表示方法体现了“式”“表”“图”的不同形态,特别是“式”与“图”的结合,体现了数形结合思想,学习过程中,应注意把它们相互结合,特别要注意加强“式”与“图”的相互转化,学生应从不同的侧面认识函数的本质.
2.学习分段函数时,学生要注意结合实例体会概念,还要注意书写的规范.
回顾
初中学过哪几种表示函数的方法?
表示函数的方法,常用的有解析法、列表法和图象法三种.
⑴解析法:就是用数学表达式表示两个变量之间的对应关系.
如,s=60t2,A=r2,S=2,y=ax2+bx+c(a≠0),y=x+2等等都是用解析式表示函数关系的.
(2)图象法:就是用图象表示两个变量之间的对应关系.
(3)列表法:就是列出表格来表示两个变量之间的对应关系.
例1
某种笔记本的单价是5元,买x(x∈{1,2,3,4,5})个笔记本需要y元.试用函数的三种表示法表示函数y=f(x).
这个函数的定义域是数集{1,2,3,4,5}.
用解析法可将函数y=f(x)表示为y=5x,
x∈{1,2,3,4,5}
用列表法可将y=f(x)表示为
笔记本数x
1
2
3
4
5
钱数y
5
10
15
20
25
用图象法可将
y=f(x)
表示为
x
y
o
1
2
3
4
5
5
10
15
20
25
·
·
·
·
·
列表法的特点:不通过计算就可以直接看出与自变量的值相对应的函数值。
图像法的特点:直观形象地表示出函数的变化情况
,有利于通过图形研究函数的某些性质。
解析法的特点
①函数关系清楚、精确;
②容易从自变量的值求出其对应的函数值;③便于研究函数的性质.
解析法是中学研究函数的主要表达方法.
所有的函数都能用解析法表示吗?
不是所有的函数都能用解析法表示.
例如,某天24整点的整点数与这一刻的气温的关系.
题型一
与函数图象有关的问题
(1).列表
x
y
o
2
其值域为[1,5]
x
y
o
2
其值域为(0,1].
(2).列表
x
-2
-1
0
1
2
y
0
-1
0
3
8
(3).列表
x
y
o
2
值域是[-1,8]
题型二
求函数的解析式
待定系数法求解析式
(1)已知一次函数f(x)满足f[f(x)]=4x+6,则f(x)的解析式为_______.
(2)已知二次函数f(x)满足f(0)=1,f(1)=2,f(2)=5,则该二次函数的解析式为_____________.
[解析] (1)设f(x)=ax+b(a≠0),
则f[f(x)]=f(ax+b)=a(ax+b)+b=a2x+ab+b=4x+6,
含参数a、b
比较系数
所以f(x)=2x+2或f(x)=-2x-6.
(2)设二次函数的解析式为f(x)=ax2+bx+c(a≠0),
换元法(或配凑法)求解析式
方程组法求函数解析式
分段函数
【题】画出函数y=|x|的图像
【解】由绝对值的概念,有y=
-x,x<0,
x,x≥0.
x
y
o
如果函数在定义域的不同的范围内,有着不同的对应关系,
则称这样的函数为分段函数.
分段函数的定义域是各段定义域的并集,值域是各段值域的并集.
题型一
分段函数的求值问题
[解析](1)f(-4)=-4+2=-2,
f(3)=2×3=6,f(-2)=-2+2=0,
f[f(-2)]=f(0)=02=0.
当a≥2时,2a=10,
可得a=5,符合题意;
[解析] f(5)=f[f(10)],f(10)=f[f(15)]=f(18)=21,
f(5)=f(21)=24.
题型二
分段函数的图像及应用
x
y
o
2
-2
°
f(x)在(-2,2]上的值域为[1,3).
x
y
o
2
1
题型三
分段函数的应用问题
例3.如图,在边长为4的正方形ABCD的边上有一点P,沿折线BCDA由点B(起点)向点A(终点)运动,设点P运动的路程为x,△APB的面积为y.
(1)求y关于x的函数关系式y=f(x);
(2)画出y=f(x)的图象;
(3)若△APB的面积不小于2,求x的取值范围.
A
B
C
D
?
?
P
x
?
?
P
P
x
y
o
2
4
6
8
10
12
2
4
6
8
例3
某市“招手即停”公共汽车的票价按下列规则制定:
(1)5公里以内(含5公里),票价2元;
(2)5公里以上,每增加5公里,票价增加1元(不足5公里的按5公里计算)
如果某条线路的总里程为20公里,请根据题意,
写出票价与里程之间的函数解析式,并画出函数的图象.
y=
2,
0
5
3,
5
<
x
≤
10
4,
10
<
x
≤
15
5,
15
<
x≤20
○
2
O
5
10
15
20
1
3
4
5
x
○
○
○
2.某质点在30s内运动速度vcm/s是时间t的函数,它的图象如右图,用解析式表示出这个函数.
30
t/s
10
20
10
30
v/cm·s-1
O
15
20
25
5
解:v(t)=
t+10,
0
≤
t<5,
3t,
5
≤
t<10,
30,
10
≤t
<20,
-3t+90,
20
≤
t≤30.
【对点练习】?
某市有A,B两家羽毛球俱乐部,两家设备和服务都很好,但收费方式不同,A俱乐部每块场地每小时收费6元;B俱乐部按月计费,一个月中20小时以内(含20小时)每块场地收费90元,超过20小时的部分,每块场地每小时2元,某企业准备下个月从这两家俱乐部中的一家租用一块场地开展活动,其活动时间不少于12小时,也不超过30小时.
(1)设在A俱乐部租一块场地开展活动x小时的收费为f(x)元(12≤x≤30),在B俱乐部租一块场地开展活动x小时的收费为g(x)元(12≤x≤30),试求f(x)与g(x)的解析式;
(2)问该企业选择哪家俱乐部比较合算,为什么?
某同学骑车上学,离开家不久,发现作业本忘家里了,于是返回家找到作业再去上学,为了赶时间他快速行驶,如图中横轴表示出发后的时间,纵轴表示离学校的距离.则较符合该同学走法的图像是( )
d0
d0
d0
d0
t0
t0
t0
t0
x
y
o
x
y
o
x
y
o
x
y
o
A
B
C
D
例4.给定函数f(x)=x+1,
g(x)=(x+1)2,
x∈R
(1)
在同一直角坐标系中画出函数
f(x),
g(x)
的图象;
(2)
用M(x)表示
f(x),
g(x)
中的较大者,记为
试分别用图象法和解析法表示函数M(x).
x
y
o
x
y
o
2.函数y=|x+1|的图象是( )
x
y
o
x
y
o
x
y
o
x
y
o
解:(1)∵f(-2)=1-2×(-2)=5,
∴f(f(-2))=f(5)=4-52=-21.
(2)当a∈R时,a2+1≥1>0,∴f(a2+1)=4-(a2+1)2=-a4-2a2+3(a∈R).
(3)①当-4≤x<0时,f(x)=1-2x,∴1<f(x)≤9;
②当x=0时,f(x)=2;
③当0<x<3时,f(x)=4-x2,
∴-5<f(x)<4.
故当-4≤x<3时,函数f(x)的值域是(-5,9].
4.如图所示,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4).
(1)求f(f(0))的值;
(2)求函数f(x)的解析式.
B
1
3
o
x
y
A
C
2
4
1
2
3
4
5
6
[解](1)直接由图中观察,可得f(f(0))=f(4)=2.
(2)设线段AB所对应的函数解析式为y=kx+b,
∴y=-2x+4(0≤x≤2).
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
