3.2.2函数的奇偶性课件-2020-2021学年高一上学期数学人教A版(2019)必修第一册(共28张PPT)
文档属性
| 名称 | 3.2.2函数的奇偶性课件-2020-2021学年高一上学期数学人教A版(2019)必修第一册(共28张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-28 00:00:00 | ||
图片预览






文档简介
(共28张PPT)
函数的奇偶性
安徽淮南第四中学
2020.10
新课程标准
核心素养
1.理解奇函数、偶函数的概念.
数学抽象
2.掌握判断某些函数奇偶性的方法.
逻辑推理
3.掌握奇偶函数的图象特征.
直观想象
4.会根据概念和图象判断简单函数的奇偶性.
逻辑推理
【学法解读】
1.学习本节知识要注意结合前面所学的知识,如单调性、函数图象、解析式等,加强它们的联系.
2.学生应理解“奇偶性”的实质,也就是图象的对称性:是关于原点的中心对称还是关于y轴的轴对称.
情境引入
生活中的对称
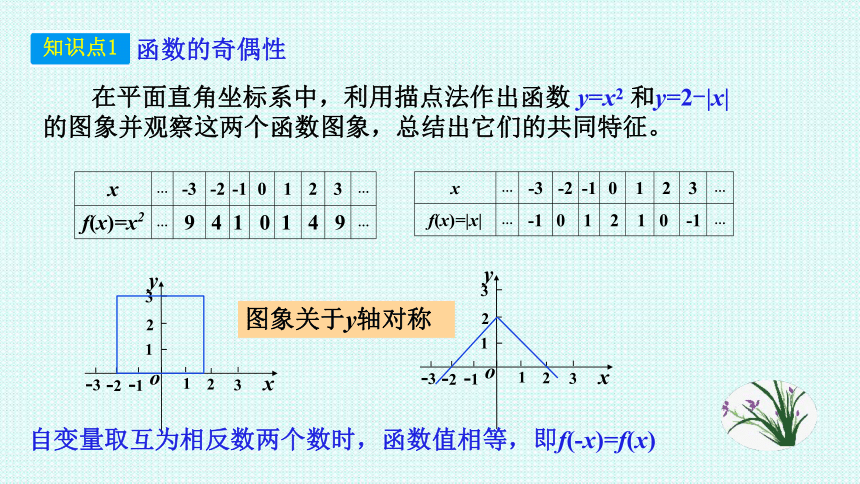
在平面直角坐标系中,利用描点法作出函数
y=x2
和y=2-|x|
的图象并观察这两个函数图象,总结出它们的共同特征。
x
…
-3
-2
-1
0
1
2
3
…
f(x)=x2
…
…
9
4
1
0
1
4
9
x
y
o
1
2
3
1
2
3
-1
-2
-3
x
…
-3
-2
-1
0
1
2
3
…
f(x)=|x|
…
…
-1
0
1
2
1
0
-1
x
y
o
1
2
3
1
2
3
-1
-2
-3
图象关于y轴对称
自变量取互为相反数两个数时,函数值相等,即f(-x)=f(x)
知识点1
函数的奇偶性
偶函数定义
一般地,设函数
f(x)的定义域为A,如果对?x∈A,都有-x∈A,
且f(-x)=f(x),即f(x)的图像关于y轴对称,那么就称f(x)为偶函数.
偶函数的图象关于y轴对称.
思考1:
(1)如果定义域内存在x0,满足f(-x0)=f(x0),
函数f(x)是偶函数吗?
不一定,必须对于定义域内的任意一个x都成立
(2).x∈A(A为定义域),-x∈A说明什么?
偶函数的定义域关于原点对称.
1.判断下列函数是否为偶函数
是
不是
2.函数y=f(x),x∈[-1,a](a>-1)是偶函数,则a等于( )
A.-1
B.0
C.1
D.无法确定
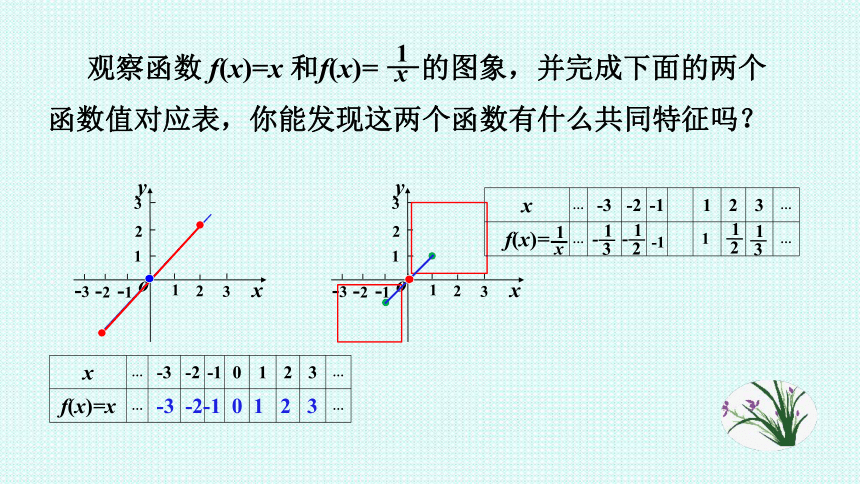
观察函数
f(x)=x
和f(x)=
的图象,并完成下面的两个函数值对应表,你能发现这两个函数有什么共同特征吗?
1
x
x
y
o
1
2
3
1
2
3
-1
-2
-3
x
y
o
1
2
3
1
2
3
-1
-2
-3
x
…
-3
-2
-1
0
1
2
3
…
f(x)=x
…
…
-3
-2-1
0
1
2
3
x
…
-3
-2
-1
1
2
3
…
f(x)=
…
…
1
x
1
3
-
1
2
-
1
3
1
2
-1
1
奇函数的定义
一般地,设函数
f(x)的定义域为A,如果对?x∈A,都有-x∈A,
且f(-x)=-f(x),即f(x)的图像关于原点对称,那么就称f(x)为奇函数.
奇函数图象特征:
奇函数的图象关于原点对称,反之,一个函数的图象关于原点对称,那么它是奇函数.
如果一个函数f(x)是奇函数或偶函数,那么我们就说函数f(x)具有奇偶性.
判定函数奇偶性基本方法:
①定义法:先看定义域是否关于原点对称,
再看f(-x)与f(x)的关系.
②图象法:
看图象是否关于原点或y轴对称.
例1:判断下列函数的奇偶性:
偶函数
偶函数
奇函数
奇函数
奇函数
既是奇函数又是
偶函数
非奇非偶
奇函数
图象法
奇函数
偶函数
O
x
y
0
x
y
0
x
y
0
x
y
0
x
y
0
x
y
知识点2
函数的奇偶性应用
题型一
奇偶函数图象的应用
例1.已知奇函数f(x)的定义域为[-5,5],且在区间[0,5]上的图象如图所示.
(1)画出在区间[-5,0]上的图象;
(2)写出使f(x)<0的x的取值集合.
x
y
o
1
2
3
1
2
3
-1
-2
-3
-4
-5
4
5
(2)由图象知,使函数值y<0的x的取值集合为(-2,0)∪(2,5).
【对点练习】已知函数y=f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.现已画出函数f(x)在y轴左侧的图象,如图所示.
(1)请补全完整函数y=f(x)的图象;
(2)根据图象写出函数y=f(x)的增区间.
(2)据图可知,单调增区间
为(-1,0),(1,+∞).
题型二
利用函数奇偶性求解析式
例2.已知函数y=f(x)的图象关于原点对称,且当x>0时,
f(x)=x2-2x+3.试求f(x)在R上的表达式.
[解析] ∵函数f(x)的图象关于原点对称.∴f(x)为奇函数,
则f(0)=0,设x<0,则-x>0,
∵x>0时,f(x)=x2-2x+3,∴f(x)=-f(-x)=-(x2+2x+3)=-x2-2x-3
已知f(x)是定义在R上的偶函数,当x≥0时,f(x)=
,试求f(x)的解析式.
2
x+1
解:设x<0,则-x>0,f(x)=f(-x)=
2
-x+1
2
-x+1
x<0
x≥0
2
x+1
f(x)=
即
f(x)=
2
|x|+1
利用奇偶性求函数解析式的关注点
(1)“求谁设谁”,即在哪个区间求解析式,x就设在哪个区间内.
(2)利用已知区间的解析式代入.
(3)利用f(x)的奇偶性写出-f(x)或f(-x),从而解出f(x).
【跟踪训练】
1.已知y=f(x)是定义在R上的奇函数,当x≥0时,f(x)=x(x-2),
则当x<0时,f(x)的解析式为
( )
A.f(x)=x(x-2)
B.f(x)=x(x+2)
C.f(x)=-x(x-2)
D.f(x)=-x(x+2)
D
2.已知f(x)是R上的偶函数,当x∈(0,+∞)时,f(x)=x2+x-1,
求x∈(-∞,0)时,f(x)的解析式.
[解析] 设x<0,则-x>0,∴f(-x)=(-x)2+(-x)-1=x2-x-1,
∵f(x)为偶函数,∴f(-x)=f(x),∴f(x)=x2-x-1.
∴当x∈(-∞,0)时,
f(x)=x2-x-1.
题型三
函数奇偶性与单调性的关系
角度1:比较大小
例3定义在R上的偶函数f(x)满足:对任意x1
,
x2∈[0,+∞)(x1≠x2),
有
<0,则
(
)
A.f(3)B.f(1)C.f(-2)D.f(3)x1-x2
f(x1)-f(x2)
偶函数,
f(-2)=f(2),
在[0,+∞)单调递减
【跟踪训练】
定义在R上的偶函数f(x)满足:对任意的x1,
x2∈(-∞,0](x1≠x2),
有(x2-x1)[f(x2)-f(x1)]>0,则当n∈N
时,有
( )
A.
f(-n)B.
f(n+1)C.
f(n-1)D.
f(n+1)角度2:解不等式
例4.定义在(-1,1)上的奇函数f(x)在整个定义域上是减函数,
若f(1-a)+f(1-3a)<0,求实数a的取值范围.
[解析] 原不等式化为f(1-3a)<-f(1-a).
因为f(x)是奇函数,所以-f(1-a)=f(a-1).
所以原不等式化为f(1-3a)转化为f(
))
或f(
)>f(
)
因为f(x)是减函数,且定义域为(-1,1),
利用区间单调性
列不等式组
已知定义在[-2,2]上的奇函数f(x)在区间[0,2]上是减函数,若f(1-m)[解] 因为f(x)在区间[-2,2]上为奇函数,且在区间[0,2]上是减函数,所以f(x)在[-2,2]上为减函数.
又f(1-m)故实数m的取值范围是[-1,
)
因为函数f(x)在实数集上是偶函数,且f(3)1或a<-2.
C
2.已知偶函数f(x)在[0,+∞)上单调递减,f(2)=0.若f(x-1)>0,则x的取值范围是________.
(-1,3)
3.已知f(x)是定义在R上的奇函数.当x>0时,f(x)=x2-
4x,则
不等式f(x)>x的解集用区间表示为————————
(-5,0)∪(5,+∞)
4.偶函数y=f(x)在[0,+∞)上是减函数,且满足f(2x)>f(x+1),
则x的取值范围为__________.?
f(2x)>f(x+1)?f(|2x|)>f(|x+1|)?|2x|<|x+1|,变形可得:3x2-2x-1<0,
(-
,1)
1
3
5.已知f(x)=x5+ax3+bx-8,且f(-2)=10,则f(2)等于( )
A.-26
B.-18
C.-10
D.10
令g(x)=x5+ax3+bx,易知g(x)是R上的奇函数,从而g(-2)=-g(2),
又f(x)=g(x)-8,∴f(-2)=g(-2)-8=10,∴g(-2)=18,
∴g(2)=-g(-2)=-18.∴f(2)=g(2)-8=-18-8=-26.
6.设f(x)是定义在R上的奇函数,且当x≥0时,f(x)=x2.
若对任意的x∈[a,a+2],不等式f(x+a)≥2f(x)恒成立,
则实数a的取值范围是________________.
已知f(x),g(x)均为R上的奇函数,且F(x)=af(x)+bg(x)+2
在区间(0,+∞)上的最大值为8,则在区间(-∞,0)上的最
小值为______.
因为f(x)和g(x)的具体表达式并没有给出,因此应充分利用
“f(x),g(x)均为R上的奇函数”这一条件,构造一个新函
数来间接求解.
由f(x),g(x)均为R上的奇函数,知af(x)+bg(x)为R上的奇函数.
由F(x)=af(x)+bg(x)+2在(0,+∞)上的最大值为8,
得F(x)-2=af(x)+bg(x)在(0,+∞)上的最大值为6.
根据奇函数的性质可知F(x)-2=af(x)+bg(x)
在(-∞,0)上的最小值为-6,故F(x)=af(x)+bg(x)+2
在(-∞,0)上的最小值为-6+2=-4.
题型四
函数图像的对称性
2.函数f(x)的图像关于点对称
若函数f(x)对定义域内任一x,都有
(1)f(a-x)=-f(a+x)?y=f(x)的图像关于点(a,0)对称;
(2)f(x)=-f(a-x)?y=f(x)的图像关于点
(
,
0)对称;
(3)f(a+x)=-f(b-x)?y=f(x)的图像关于点
(
,0)对称
a
2
a+b
2
1.已知函数f(x+1)是偶函数,则函数f(x)的对称轴是
.
直线x=1
2.已知函数f(x+1)是奇函数,则函数f(x)的对称中心是
.
(1,0)
∵f(x+1)是奇函数,∴f(-x+1)=-f(x+1),即f(-x+1)+f(x+1)=0
f(x+1)表示是f(x)向左平移一个单位
3.若函数f(x)=x2-ax-b满足对于任意的实数x都有f(1+x)=f(1-x),且f(x)的最小值为-2,求实数a,b的值.
f(x+1)=f(1-x),关于直线x=1对称,且最小值为-2,
则f(x)=(x-1)2-2=x2-2x-1,a=2,b=1
已知函数f(x)对于任意的实数x、y,都有f(x+y)=f(x)+f(y)
(1)求f(0)的值;
(2)试判断函数f(x)的奇偶性;
(3)若x>0都有f(x)>0,试判断函数的单调性.
(1).f(0)=0
(2)令y
=
-x,则f(x-x)=f(x)+f(-x)=0,奇函数
设0x1>0
,
f(x2)-f(x1)>0
,
f(x2)=f[(x2-x1)+
x1]=f(x2-x1)+f(x1)>f(x1),
函数
是增函数
函数的奇偶性
安徽淮南第四中学
2020.10
新课程标准
核心素养
1.理解奇函数、偶函数的概念.
数学抽象
2.掌握判断某些函数奇偶性的方法.
逻辑推理
3.掌握奇偶函数的图象特征.
直观想象
4.会根据概念和图象判断简单函数的奇偶性.
逻辑推理
【学法解读】
1.学习本节知识要注意结合前面所学的知识,如单调性、函数图象、解析式等,加强它们的联系.
2.学生应理解“奇偶性”的实质,也就是图象的对称性:是关于原点的中心对称还是关于y轴的轴对称.
情境引入
生活中的对称
在平面直角坐标系中,利用描点法作出函数
y=x2
和y=2-|x|
的图象并观察这两个函数图象,总结出它们的共同特征。
x
…
-3
-2
-1
0
1
2
3
…
f(x)=x2
…
…
9
4
1
0
1
4
9
x
y
o
1
2
3
1
2
3
-1
-2
-3
x
…
-3
-2
-1
0
1
2
3
…
f(x)=|x|
…
…
-1
0
1
2
1
0
-1
x
y
o
1
2
3
1
2
3
-1
-2
-3
图象关于y轴对称
自变量取互为相反数两个数时,函数值相等,即f(-x)=f(x)
知识点1
函数的奇偶性
偶函数定义
一般地,设函数
f(x)的定义域为A,如果对?x∈A,都有-x∈A,
且f(-x)=f(x),即f(x)的图像关于y轴对称,那么就称f(x)为偶函数.
偶函数的图象关于y轴对称.
思考1:
(1)如果定义域内存在x0,满足f(-x0)=f(x0),
函数f(x)是偶函数吗?
不一定,必须对于定义域内的任意一个x都成立
(2).x∈A(A为定义域),-x∈A说明什么?
偶函数的定义域关于原点对称.
1.判断下列函数是否为偶函数
是
不是
2.函数y=f(x),x∈[-1,a](a>-1)是偶函数,则a等于( )
A.-1
B.0
C.1
D.无法确定
观察函数
f(x)=x
和f(x)=
的图象,并完成下面的两个函数值对应表,你能发现这两个函数有什么共同特征吗?
1
x
x
y
o
1
2
3
1
2
3
-1
-2
-3
x
y
o
1
2
3
1
2
3
-1
-2
-3
x
…
-3
-2
-1
0
1
2
3
…
f(x)=x
…
…
-3
-2-1
0
1
2
3
x
…
-3
-2
-1
1
2
3
…
f(x)=
…
…
1
x
1
3
-
1
2
-
1
3
1
2
-1
1
奇函数的定义
一般地,设函数
f(x)的定义域为A,如果对?x∈A,都有-x∈A,
且f(-x)=-f(x),即f(x)的图像关于原点对称,那么就称f(x)为奇函数.
奇函数图象特征:
奇函数的图象关于原点对称,反之,一个函数的图象关于原点对称,那么它是奇函数.
如果一个函数f(x)是奇函数或偶函数,那么我们就说函数f(x)具有奇偶性.
判定函数奇偶性基本方法:
①定义法:先看定义域是否关于原点对称,
再看f(-x)与f(x)的关系.
②图象法:
看图象是否关于原点或y轴对称.
例1:判断下列函数的奇偶性:
偶函数
偶函数
奇函数
奇函数
奇函数
既是奇函数又是
偶函数
非奇非偶
奇函数
图象法
奇函数
偶函数
O
x
y
0
x
y
0
x
y
0
x
y
0
x
y
0
x
y
知识点2
函数的奇偶性应用
题型一
奇偶函数图象的应用
例1.已知奇函数f(x)的定义域为[-5,5],且在区间[0,5]上的图象如图所示.
(1)画出在区间[-5,0]上的图象;
(2)写出使f(x)<0的x的取值集合.
x
y
o
1
2
3
1
2
3
-1
-2
-3
-4
-5
4
5
(2)由图象知,使函数值y<0的x的取值集合为(-2,0)∪(2,5).
【对点练习】已知函数y=f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.现已画出函数f(x)在y轴左侧的图象,如图所示.
(1)请补全完整函数y=f(x)的图象;
(2)根据图象写出函数y=f(x)的增区间.
(2)据图可知,单调增区间
为(-1,0),(1,+∞).
题型二
利用函数奇偶性求解析式
例2.已知函数y=f(x)的图象关于原点对称,且当x>0时,
f(x)=x2-2x+3.试求f(x)在R上的表达式.
[解析] ∵函数f(x)的图象关于原点对称.∴f(x)为奇函数,
则f(0)=0,设x<0,则-x>0,
∵x>0时,f(x)=x2-2x+3,∴f(x)=-f(-x)=-(x2+2x+3)=-x2-2x-3
已知f(x)是定义在R上的偶函数,当x≥0时,f(x)=
,试求f(x)的解析式.
2
x+1
解:设x<0,则-x>0,f(x)=f(-x)=
2
-x+1
2
-x+1
x<0
x≥0
2
x+1
f(x)=
即
f(x)=
2
|x|+1
利用奇偶性求函数解析式的关注点
(1)“求谁设谁”,即在哪个区间求解析式,x就设在哪个区间内.
(2)利用已知区间的解析式代入.
(3)利用f(x)的奇偶性写出-f(x)或f(-x),从而解出f(x).
【跟踪训练】
1.已知y=f(x)是定义在R上的奇函数,当x≥0时,f(x)=x(x-2),
则当x<0时,f(x)的解析式为
( )
A.f(x)=x(x-2)
B.f(x)=x(x+2)
C.f(x)=-x(x-2)
D.f(x)=-x(x+2)
D
2.已知f(x)是R上的偶函数,当x∈(0,+∞)时,f(x)=x2+x-1,
求x∈(-∞,0)时,f(x)的解析式.
[解析] 设x<0,则-x>0,∴f(-x)=(-x)2+(-x)-1=x2-x-1,
∵f(x)为偶函数,∴f(-x)=f(x),∴f(x)=x2-x-1.
∴当x∈(-∞,0)时,
f(x)=x2-x-1.
题型三
函数奇偶性与单调性的关系
角度1:比较大小
例3定义在R上的偶函数f(x)满足:对任意x1
,
x2∈[0,+∞)(x1≠x2),
有
<0,则
(
)
A.f(3)
f(x1)-f(x2)
偶函数,
f(-2)=f(2),
在[0,+∞)单调递减
【跟踪训练】
定义在R上的偶函数f(x)满足:对任意的x1,
x2∈(-∞,0](x1≠x2),
有(x2-x1)[f(x2)-f(x1)]>0,则当n∈N
时,有
( )
A.
f(-n)
f(n+1)
f(n-1)
f(n+1)
例4.定义在(-1,1)上的奇函数f(x)在整个定义域上是减函数,
若f(1-a)+f(1-3a)<0,求实数a的取值范围.
[解析] 原不等式化为f(1-3a)<-f(1-a).
因为f(x)是奇函数,所以-f(1-a)=f(a-1).
所以原不等式化为f(1-3a)
)
或f(
)>f(
)
因为f(x)是减函数,且定义域为(-1,1),
利用区间单调性
列不等式组
已知定义在[-2,2]上的奇函数f(x)在区间[0,2]上是减函数,若f(1-m)
又f(1-m)
)
因为函数f(x)在实数集上是偶函数,且f(3)
C
2.已知偶函数f(x)在[0,+∞)上单调递减,f(2)=0.若f(x-1)>0,则x的取值范围是________.
(-1,3)
3.已知f(x)是定义在R上的奇函数.当x>0时,f(x)=x2-
4x,则
不等式f(x)>x的解集用区间表示为————————
(-5,0)∪(5,+∞)
4.偶函数y=f(x)在[0,+∞)上是减函数,且满足f(2x)>f(x+1),
则x的取值范围为__________.?
f(2x)>f(x+1)?f(|2x|)>f(|x+1|)?|2x|<|x+1|,变形可得:3x2-2x-1<0,
(-
,1)
1
3
5.已知f(x)=x5+ax3+bx-8,且f(-2)=10,则f(2)等于( )
A.-26
B.-18
C.-10
D.10
令g(x)=x5+ax3+bx,易知g(x)是R上的奇函数,从而g(-2)=-g(2),
又f(x)=g(x)-8,∴f(-2)=g(-2)-8=10,∴g(-2)=18,
∴g(2)=-g(-2)=-18.∴f(2)=g(2)-8=-18-8=-26.
6.设f(x)是定义在R上的奇函数,且当x≥0时,f(x)=x2.
若对任意的x∈[a,a+2],不等式f(x+a)≥2f(x)恒成立,
则实数a的取值范围是________________.
已知f(x),g(x)均为R上的奇函数,且F(x)=af(x)+bg(x)+2
在区间(0,+∞)上的最大值为8,则在区间(-∞,0)上的最
小值为______.
因为f(x)和g(x)的具体表达式并没有给出,因此应充分利用
“f(x),g(x)均为R上的奇函数”这一条件,构造一个新函
数来间接求解.
由f(x),g(x)均为R上的奇函数,知af(x)+bg(x)为R上的奇函数.
由F(x)=af(x)+bg(x)+2在(0,+∞)上的最大值为8,
得F(x)-2=af(x)+bg(x)在(0,+∞)上的最大值为6.
根据奇函数的性质可知F(x)-2=af(x)+bg(x)
在(-∞,0)上的最小值为-6,故F(x)=af(x)+bg(x)+2
在(-∞,0)上的最小值为-6+2=-4.
题型四
函数图像的对称性
2.函数f(x)的图像关于点对称
若函数f(x)对定义域内任一x,都有
(1)f(a-x)=-f(a+x)?y=f(x)的图像关于点(a,0)对称;
(2)f(x)=-f(a-x)?y=f(x)的图像关于点
(
,
0)对称;
(3)f(a+x)=-f(b-x)?y=f(x)的图像关于点
(
,0)对称
a
2
a+b
2
1.已知函数f(x+1)是偶函数,则函数f(x)的对称轴是
.
直线x=1
2.已知函数f(x+1)是奇函数,则函数f(x)的对称中心是
.
(1,0)
∵f(x+1)是奇函数,∴f(-x+1)=-f(x+1),即f(-x+1)+f(x+1)=0
f(x+1)表示是f(x)向左平移一个单位
3.若函数f(x)=x2-ax-b满足对于任意的实数x都有f(1+x)=f(1-x),且f(x)的最小值为-2,求实数a,b的值.
f(x+1)=f(1-x),关于直线x=1对称,且最小值为-2,
则f(x)=(x-1)2-2=x2-2x-1,a=2,b=1
已知函数f(x)对于任意的实数x、y,都有f(x+y)=f(x)+f(y)
(1)求f(0)的值;
(2)试判断函数f(x)的奇偶性;
(3)若x>0都有f(x)>0,试判断函数的单调性.
(1).f(0)=0
(2)令y
=
-x,则f(x-x)=f(x)+f(-x)=0,奇函数
设0
,
f(x2)-f(x1)>0
,
f(x2)=f[(x2-x1)+
x1]=f(x2-x1)+f(x1)>f(x1),
函数
是增函数
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
