3.4函数的应用(一)课件-2020-2021学年高一上学期数学人教A版(2019)必修第一册(共16张PPT)
文档属性
| 名称 | 3.4函数的应用(一)课件-2020-2021学年高一上学期数学人教A版(2019)必修第一册(共16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-28 22:13:07 | ||
图片预览






文档简介
(共16张PPT)
函数的应用(一)
安徽淮南第四中学
2020.10
新课程标准
核心素养
1.了解函数模型(如一次函数、二次函数、幂函数、分段函数等是现实生活中普遍使用的函数模型)的广泛应用.
数学抽象
2.能够利用给定的函数模型或建立确定的函数模型解决实际问题.
数学建模
【学法解读】
1.学生应理解如何用函数描述客观事物的变化规律,体会函数与现实世界的联系.
2.会用已学过的一次函数、二次函数、幂函数、分段函数处理有关实际应用问题.
一次函数模型
形如y=kx+b的函数为________________,其中k≠0.
知识点1
一次函数模型
类型一
一次函数模型的应用
【例1】 某厂日生产文具盒的总成本y(元)与日产量x(套)之间的关系为y=6x+30
000.而出厂价格为每套12元,要使该厂不亏本,至少日生产文具盒( )
A.2
000套
B.3
000套
C.4
000套
D.5
000套
1.A,B两地相距150千米,某人开汽车以60千米/小时的速度从A地到达B地,在B地停留1小时后再以50千米/小时的速度返回A地.
(1)试把汽车与A地的距离y(单位:千米)表示为时间x(单位:小时)的函数;
(2)根据(1)中的函数解析式,求出汽车距离A地100千米时x的值.
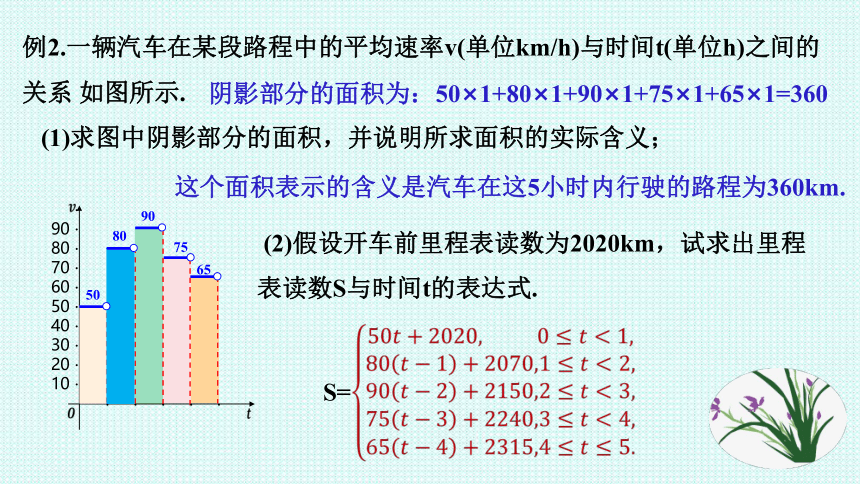
例2.一辆汽车在某段路程中的平均速率v(单位km/h)与时间t(单位h)之间的
关系
如图所示.
(1)求图中阴影部分的面积,并说明所求面积的实际含义;
?
?
?
90
80
70
60
50
40
30
20
10
·
·
·
·
·
·
·
·
·
·
50
75
65
80
90
·
·
·
·
·
阴影部分的面积为:50×1+80×1+90×1+75×1+65×1=360
这个面积表示的含义是汽车在这5小时内行驶的路程为360km.
(2)假设开车前里程表读数为2020km,试求出里程表读数S与时间t的表达式.
S=
类型二
二次函数模型的应用
例3.某水果批发商销售每箱进价为40元的苹果,假设每箱售价不得低于50元且不得高于55元.市场调查发现,若每箱以50元的价格销售,平均每天销售90箱,价格每提高1元,平均每天少销售3箱.
(1)求平均每天的销售量y(箱)与销售单价x(元/箱)之间的函数关系式;
(2)求该批发商平均每天的销售利润w(元)与销售单价x(元/箱)之间的函数关系式;
(3)当每箱苹果的售价为多少元时,可以获得最大利润?最大利润是多少?
[解] (1)根据题意,得y=90-3(x-50),
化简,得y=-3x+240(50≤x≤55,x∈N).
(2)因为该批发商平均每天的销售利润=平均每天的销售量×每箱销售利润.所以w=(x-40)(-3x+240)=-3x2+360x-9
600(50≤x≤55,x∈N).
(3)因为w=-3x2+360x-9
600=-3(x-60)2+1
200,
所以当x<60时,w随x的增大而增大.又50≤x≤55,x∈N,所以
当x=55时,w有最大值,最大值为1
125.所以当每箱苹果的售价
为55元时,可以获得最大利润,且最大利润为1
125元.
2.某租车公司拥有汽车100辆,当每辆车的月租金为3
000元时,可全部租出,当每辆车的月租金每增加60元时,未租出的车将会增加一辆,租出的车每月需要维护费160元,未租出的车每月需要维护费40元.
①当每辆车的月租金定为3
900元时,能租出多少辆车?
②当每辆车的月租金为多少元时,租车公司的月收益最大?最大月收益是多少?
解:①租金增加了900元,900÷60=15,所以未租出的车有15辆,一共能租出85辆.
②设租金提高后有x辆未租出,则已租出(100-x)辆.租赁公司的月收益为y元,y=(3
000+60x)(100-x)-160(100-x)-40x,其中x∈[0,100],x∈N,整理得y=-60x2+3
120x+284
000=-60(x-26)2+324
560,当x=26时,y=324
560,即最大月收益为324
560元.此时,月租金为3
000+60×26=4
560(元).
如图所示,已知边长为8
m
的正方形钢板有一个角被锈蚀,其中AE=4
m,CD=6
m.为合理利用这块钢板,在五边形ABCDE内截取一个矩形BNPM,使点P在边DE上.
(1)设MP=x
m,PN=y
m,将y表示成x的函数,求该函数的解析式及定义域;
(2)求矩形BNPM面积的最大值.
A
M
P
N
B
C
D
E
F
解:(1)如图,作PQ⊥AF于点Q.
所以PQ=(8-y)m,EQ=(x-4)m
.
又因为△EPQ∽△EDF,
Q
EQ
EF
PQ
FD
=
x-4
4
8-y
2
=
y=
-
x+10
1
2
(2)设矩形BNPM的面积为S
m2,
则S(x)=xy=
-
(x-10)2+50,
1
2
{x|4≤x≤8}.
对称轴为直线x=10,所以当x∈[4,8]时,S(x)单调递增.
所以当x=8时,矩形BNPM的面积取得最大值,为
48
m2.
类型三
幂函数模型的应用
例4.某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比.已知投资1万元时两类产品的收益分别为0.125万元和0.5万元.
(1)分别写出两类产品的收益与投资额x的函数关系式;
(2)该家庭现有20万元资金,全部用于理财投资,问:怎么分配资金能使投资获得最大收益,最大收益是多少万元?
【对点练习】
在固定压力差(压力差为常数)下,当气体通过圆形管道时,其流量速率R与管道半径r的四次方成正比.
(1)写出函数解析式;
(2)假设气体在半径为3
cm的管道中,流量速率为400
cm3/s.求该气体通过半径为r
cm的管道时,其流量速率R的解析式;
(3)已知(2)中的气体通过的管道半径为5
cm,计算该气体的流量速率.(结果保留整数)
[解析] (1)由题意,得R=kr4(k是大于0的常数).
类型四
分段函数模型的应用
【对点练习】某市居民自来水收费标准如下:每户每月用水量不超过4
t时,每吨3元,当用水量超过4
t时,超过部分每吨4元.现甲、乙两户共交水费y元,已知甲、乙两户该月用水量分别为5x
t,3x
t.
(1)求y关于x的函数关系式;
(2)若甲、乙两户该月共交水费40元,分别求出甲、乙两户该月的用水量和水费.
[解析] (1)当甲户用水量不超过4
t,即5x≤4时,乙户用水量也不超过4
t,
y=(5x+3x)×3=24x;
当甲户的用水量超过4
t而乙户的用水量不超过4
t,
当甲、乙两户的用水量均超过4
t,即3x>4时,
y=4×3×2+(5x-4)×4+(3x-4)×4=32x-8.
即5x>4且3x≤4时,y=4×3+3x×3+4×(5x-4)=29x-4;
函数的应用(一)
安徽淮南第四中学
2020.10
新课程标准
核心素养
1.了解函数模型(如一次函数、二次函数、幂函数、分段函数等是现实生活中普遍使用的函数模型)的广泛应用.
数学抽象
2.能够利用给定的函数模型或建立确定的函数模型解决实际问题.
数学建模
【学法解读】
1.学生应理解如何用函数描述客观事物的变化规律,体会函数与现实世界的联系.
2.会用已学过的一次函数、二次函数、幂函数、分段函数处理有关实际应用问题.
一次函数模型
形如y=kx+b的函数为________________,其中k≠0.
知识点1
一次函数模型
类型一
一次函数模型的应用
【例1】 某厂日生产文具盒的总成本y(元)与日产量x(套)之间的关系为y=6x+30
000.而出厂价格为每套12元,要使该厂不亏本,至少日生产文具盒( )
A.2
000套
B.3
000套
C.4
000套
D.5
000套
1.A,B两地相距150千米,某人开汽车以60千米/小时的速度从A地到达B地,在B地停留1小时后再以50千米/小时的速度返回A地.
(1)试把汽车与A地的距离y(单位:千米)表示为时间x(单位:小时)的函数;
(2)根据(1)中的函数解析式,求出汽车距离A地100千米时x的值.
例2.一辆汽车在某段路程中的平均速率v(单位km/h)与时间t(单位h)之间的
关系
如图所示.
(1)求图中阴影部分的面积,并说明所求面积的实际含义;
?
?
?
90
80
70
60
50
40
30
20
10
·
·
·
·
·
·
·
·
·
·
50
75
65
80
90
·
·
·
·
·
阴影部分的面积为:50×1+80×1+90×1+75×1+65×1=360
这个面积表示的含义是汽车在这5小时内行驶的路程为360km.
(2)假设开车前里程表读数为2020km,试求出里程表读数S与时间t的表达式.
S=
类型二
二次函数模型的应用
例3.某水果批发商销售每箱进价为40元的苹果,假设每箱售价不得低于50元且不得高于55元.市场调查发现,若每箱以50元的价格销售,平均每天销售90箱,价格每提高1元,平均每天少销售3箱.
(1)求平均每天的销售量y(箱)与销售单价x(元/箱)之间的函数关系式;
(2)求该批发商平均每天的销售利润w(元)与销售单价x(元/箱)之间的函数关系式;
(3)当每箱苹果的售价为多少元时,可以获得最大利润?最大利润是多少?
[解] (1)根据题意,得y=90-3(x-50),
化简,得y=-3x+240(50≤x≤55,x∈N).
(2)因为该批发商平均每天的销售利润=平均每天的销售量×每箱销售利润.所以w=(x-40)(-3x+240)=-3x2+360x-9
600(50≤x≤55,x∈N).
(3)因为w=-3x2+360x-9
600=-3(x-60)2+1
200,
所以当x<60时,w随x的增大而增大.又50≤x≤55,x∈N,所以
当x=55时,w有最大值,最大值为1
125.所以当每箱苹果的售价
为55元时,可以获得最大利润,且最大利润为1
125元.
2.某租车公司拥有汽车100辆,当每辆车的月租金为3
000元时,可全部租出,当每辆车的月租金每增加60元时,未租出的车将会增加一辆,租出的车每月需要维护费160元,未租出的车每月需要维护费40元.
①当每辆车的月租金定为3
900元时,能租出多少辆车?
②当每辆车的月租金为多少元时,租车公司的月收益最大?最大月收益是多少?
解:①租金增加了900元,900÷60=15,所以未租出的车有15辆,一共能租出85辆.
②设租金提高后有x辆未租出,则已租出(100-x)辆.租赁公司的月收益为y元,y=(3
000+60x)(100-x)-160(100-x)-40x,其中x∈[0,100],x∈N,整理得y=-60x2+3
120x+284
000=-60(x-26)2+324
560,当x=26时,y=324
560,即最大月收益为324
560元.此时,月租金为3
000+60×26=4
560(元).
如图所示,已知边长为8
m
的正方形钢板有一个角被锈蚀,其中AE=4
m,CD=6
m.为合理利用这块钢板,在五边形ABCDE内截取一个矩形BNPM,使点P在边DE上.
(1)设MP=x
m,PN=y
m,将y表示成x的函数,求该函数的解析式及定义域;
(2)求矩形BNPM面积的最大值.
A
M
P
N
B
C
D
E
F
解:(1)如图,作PQ⊥AF于点Q.
所以PQ=(8-y)m,EQ=(x-4)m
.
又因为△EPQ∽△EDF,
Q
EQ
EF
PQ
FD
=
x-4
4
8-y
2
=
y=
-
x+10
1
2
(2)设矩形BNPM的面积为S
m2,
则S(x)=xy=
-
(x-10)2+50,
1
2
{x|4≤x≤8}.
对称轴为直线x=10,所以当x∈[4,8]时,S(x)单调递增.
所以当x=8时,矩形BNPM的面积取得最大值,为
48
m2.
类型三
幂函数模型的应用
例4.某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比.已知投资1万元时两类产品的收益分别为0.125万元和0.5万元.
(1)分别写出两类产品的收益与投资额x的函数关系式;
(2)该家庭现有20万元资金,全部用于理财投资,问:怎么分配资金能使投资获得最大收益,最大收益是多少万元?
【对点练习】
在固定压力差(压力差为常数)下,当气体通过圆形管道时,其流量速率R与管道半径r的四次方成正比.
(1)写出函数解析式;
(2)假设气体在半径为3
cm的管道中,流量速率为400
cm3/s.求该气体通过半径为r
cm的管道时,其流量速率R的解析式;
(3)已知(2)中的气体通过的管道半径为5
cm,计算该气体的流量速率.(结果保留整数)
[解析] (1)由题意,得R=kr4(k是大于0的常数).
类型四
分段函数模型的应用
【对点练习】某市居民自来水收费标准如下:每户每月用水量不超过4
t时,每吨3元,当用水量超过4
t时,超过部分每吨4元.现甲、乙两户共交水费y元,已知甲、乙两户该月用水量分别为5x
t,3x
t.
(1)求y关于x的函数关系式;
(2)若甲、乙两户该月共交水费40元,分别求出甲、乙两户该月的用水量和水费.
[解析] (1)当甲户用水量不超过4
t,即5x≤4时,乙户用水量也不超过4
t,
y=(5x+3x)×3=24x;
当甲户的用水量超过4
t而乙户的用水量不超过4
t,
当甲、乙两户的用水量均超过4
t,即3x>4时,
y=4×3×2+(5x-4)×4+(3x-4)×4=32x-8.
即5x>4且3x≤4时,y=4×3+3x×3+4×(5x-4)=29x-4;
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
