5.2.1三角函数的概念课件-2020-2021学年高一上学期数学人教A版(2019)必修第一册(共24张PPT)
文档属性
| 名称 | 5.2.1三角函数的概念课件-2020-2021学年高一上学期数学人教A版(2019)必修第一册(共24张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-28 22:19:57 | ||
图片预览




文档简介
(共24张PPT)
三角函数的概念
安徽淮南第四中学
2020.11
新课程标准
核心素养
1.借助单位圆理解三角函数(正弦、余弦、正切)的定义.
数学建模
2.理解三角函数的概念.
数学抽象
3.熟练掌握三角函数值在各象限的符号.
直观想象
4.通过对任意角的三角函数定义的理解,掌握终边相同的角的同一三角函数值相等.
数学运算
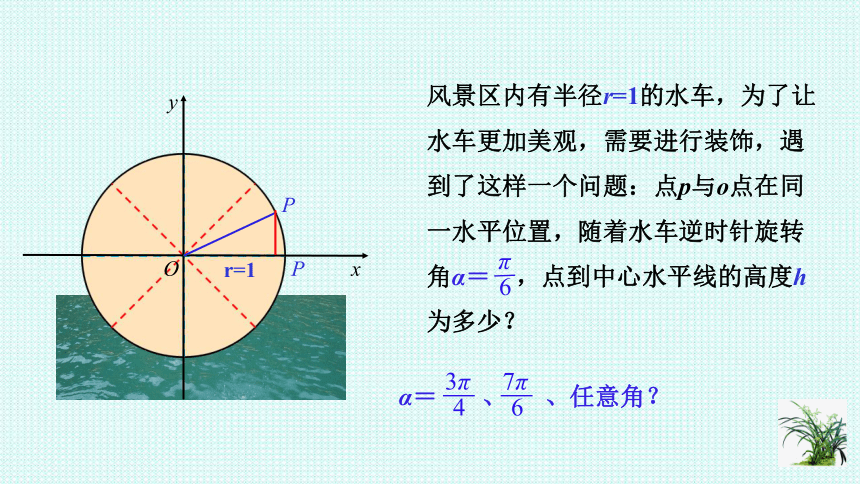
O
x
y
r=1
P
风景区内有半径r=1的水车,为了让水车更加美观,需要进行装饰,遇到了这样一个问题:点p与o点在同一水平位置,随着水车逆时针旋转角α=
,点到中心水平线的高度h为多少?
π
6
P
α=
、
、任意角?
3π
4
7π
6
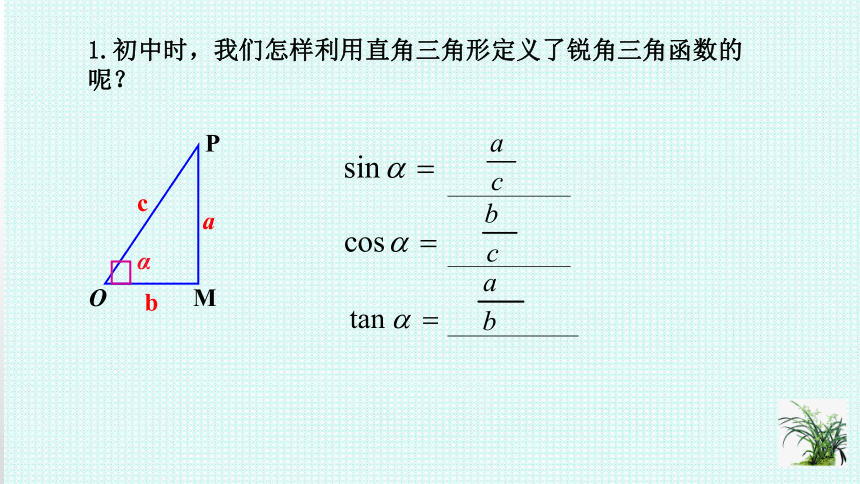
1.初中时,我们怎样利用直角三角形定义了锐角三角函数的呢?
α
O
M
P
a
b
c
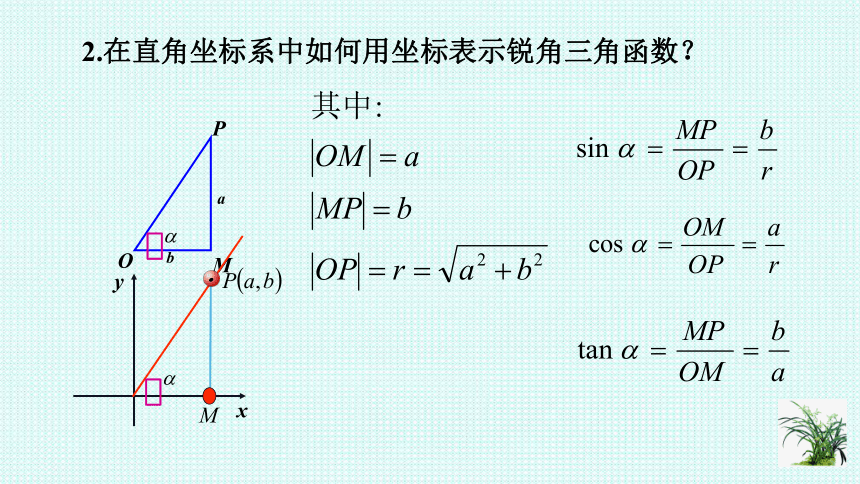
2.在直角坐标系中如何用坐标表示锐角三角函数?
x
y
O
a
b
M
P
﹒
﹒
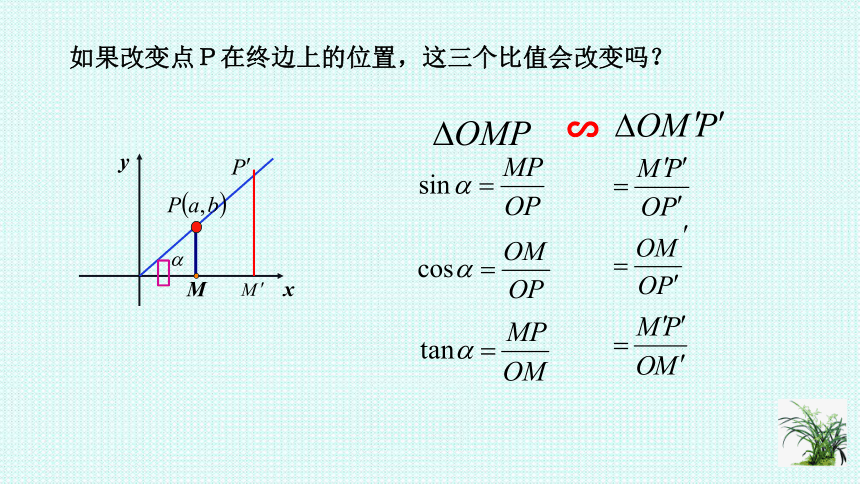
如果改变点P在终边上的位置,这三个比值会改变吗?
x
y
M
∽
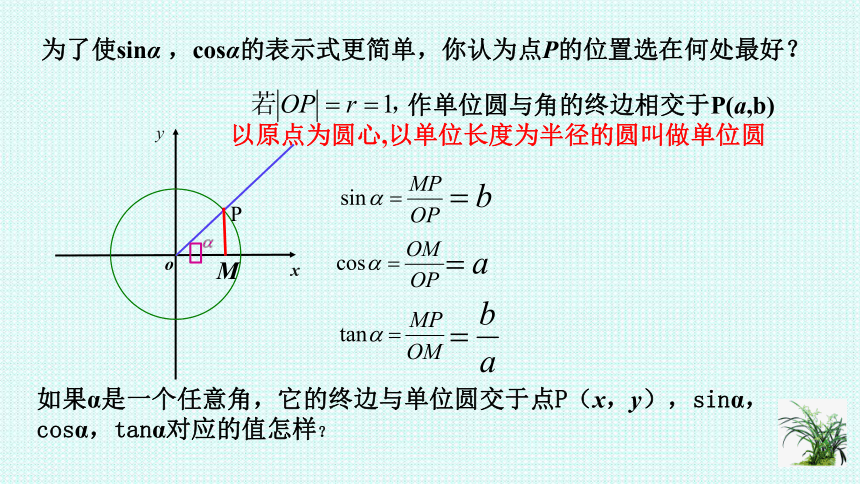
为了使sinα
,cosα的表示式更简单,你认为点P的位置选在何处最好?
y
x
o
P
M
作单位圆与角的终边相交于P(a,b)
以原点为圆心,以单位长度为半径的圆叫做单位圆
如果α是一个任意角,它的终边与单位圆交于点P(x,y),sinα,cosα,tanα对应的值怎样?
y
x
o
三角函数的定义
对应关系
,
,
都是以角为自变量,以单位圆上的点的坐标或坐标的比值为函数值的函数,分别称为正弦函数、余弦函数和正切函数,并统称为三角函数.
注意:无论角a是第几象限角,它的三角函数的定义都是一样。
说
明
(1).正弦就是交点的纵坐标,余弦就是交点的横坐标,
正切就是交点的纵坐标与横坐标的比值.
(2).正弦、余弦总有意义.当
的终边在
轴上时,点P
的横坐标等
于0,
无意义,此时
(3).由于角的集合与实数集之间可以建立一一对应关系,三角函数可以看成是自变量为实数的函数.
x
y
o
的终边
设角
是一个任意角,
是终边上的任意一点,
点
与原点的距离
.
那么①
叫做
的正弦,即
②
叫做
的余弦,即
③
叫做
的正弦,即
任意角
的三角函数值仅与
有关,而与点
在角的终边上的位置无关.
例1.求
的正弦、余弦和正切值.
﹒
﹒
解:在直角坐标系中,作
,易知
的终边与单位圆的交点坐标为
所以
例2.已知角
的终边经过点
,求角
的正弦、余弦和正切值
.
解:由已知可得
P0
P
M
M0
几个特殊角的三角函数值
角α
0o
30o
45o
60o
90o
180o
270o
360o
角α的弧度数
sinα
cosα
tanα
1
2
3
2
3
3
2
2
2
2
1
3
2
1
2
3
1
0
0
0
0
-1
-1
1
0
0
1.
角α的终边经过点P(0,
b)则(
)
A.sin
α=0
B.sin
α=1
C.sin
α=-1
D.sin
α=±1
D
2.若角600o的终边上有一点(-4,
a),则a的值是(
)
600o的终边落在第三象限,∴a<0,
60°
3.已知角α的终边经过点P(2a,-3a),求角α的正弦、余弦、正切值.
x
=2a,
y
=
-3a
r=
=
=
x2+y2
(2a)2+(-3a)2
a
13
当a<0时,sinα=
,cosα=-
,
tanα=-
3
13
13
3
2
2
13
13
当a>0时,sinα=-
,cosα=
tanα=-
3
13
13
2
13
13
3
2
4.已知角的终边落在直线y=2x上,求sinα、c
osα、tanα的值.
[解析] 当角的终边在第一象限时,在角的终边上取点P(1,2),
(
)
(
)
三角函数在各象限内的符号:
y
x
o
y
x
o
y
x
o
+
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
+
-
-
+
+
-
-
+
+
-
-
例3
确定下列三角函数值的符号:
(1)
(2)
(3)
(1)因为250°是第三象限角,所以cosα<0;
解:
(2)∵-672?=-2×360?+48?,∴tan(-672?)>0.
π
4
(3)因为-
是第四象限角,所以
π
4
sin(-
)<0
探究
根据三角函数的定义:
终边相同的角的同一三角函数值是否相等?
∵终边相同的角的集合为:
终边相同
点的坐标相同
三角函数值相同
终边相同的角的三角函数关系
终边相同的角的同一三角函数值相等,由此得到一组公式(公式一):
(其中
)
利用公式一,作用在于可将求任意角的三角函数值,转化为求0~2π
(或0°~360°)范围内的三角函数值.
(1)
cos390°=cos(360°+30°)=cos30°=
3
2
(2)
7π
4
sin(-
)=sin(-2π+
)=sin
=
π
4
π
4
2
2
(3)tan(-675°)=tan(-2×360°+45°)=tan45°=1
(4)tan3π=tan(2π+π)=tanπ=0
C
2.已知角α的终边经过点(3a-9,a+2),且cosα≤0,sinα>0,则a的取值范围是____________
(-2,3]
3a-9≤0
a+2>0
归纳
总结
1.
内容总结:
①三角函数的概念.
②三角函数的定义域及三角函数值在各象限的符号.
③诱导公式一.
2
.方法总结:
运用了定义法、公式法、数形结合法解题.
3
.体现的数学思想:
划归的思想,数形结合的思想.
三角函数的概念
安徽淮南第四中学
2020.11
新课程标准
核心素养
1.借助单位圆理解三角函数(正弦、余弦、正切)的定义.
数学建模
2.理解三角函数的概念.
数学抽象
3.熟练掌握三角函数值在各象限的符号.
直观想象
4.通过对任意角的三角函数定义的理解,掌握终边相同的角的同一三角函数值相等.
数学运算
O
x
y
r=1
P
风景区内有半径r=1的水车,为了让水车更加美观,需要进行装饰,遇到了这样一个问题:点p与o点在同一水平位置,随着水车逆时针旋转角α=
,点到中心水平线的高度h为多少?
π
6
P
α=
、
、任意角?
3π
4
7π
6
1.初中时,我们怎样利用直角三角形定义了锐角三角函数的呢?
α
O
M
P
a
b
c
2.在直角坐标系中如何用坐标表示锐角三角函数?
x
y
O
a
b
M
P
﹒
﹒
如果改变点P在终边上的位置,这三个比值会改变吗?
x
y
M
∽
为了使sinα
,cosα的表示式更简单,你认为点P的位置选在何处最好?
y
x
o
P
M
作单位圆与角的终边相交于P(a,b)
以原点为圆心,以单位长度为半径的圆叫做单位圆
如果α是一个任意角,它的终边与单位圆交于点P(x,y),sinα,cosα,tanα对应的值怎样?
y
x
o
三角函数的定义
对应关系
,
,
都是以角为自变量,以单位圆上的点的坐标或坐标的比值为函数值的函数,分别称为正弦函数、余弦函数和正切函数,并统称为三角函数.
注意:无论角a是第几象限角,它的三角函数的定义都是一样。
说
明
(1).正弦就是交点的纵坐标,余弦就是交点的横坐标,
正切就是交点的纵坐标与横坐标的比值.
(2).正弦、余弦总有意义.当
的终边在
轴上时,点P
的横坐标等
于0,
无意义,此时
(3).由于角的集合与实数集之间可以建立一一对应关系,三角函数可以看成是自变量为实数的函数.
x
y
o
的终边
设角
是一个任意角,
是终边上的任意一点,
点
与原点的距离
.
那么①
叫做
的正弦,即
②
叫做
的余弦,即
③
叫做
的正弦,即
任意角
的三角函数值仅与
有关,而与点
在角的终边上的位置无关.
例1.求
的正弦、余弦和正切值.
﹒
﹒
解:在直角坐标系中,作
,易知
的终边与单位圆的交点坐标为
所以
例2.已知角
的终边经过点
,求角
的正弦、余弦和正切值
.
解:由已知可得
P0
P
M
M0
几个特殊角的三角函数值
角α
0o
30o
45o
60o
90o
180o
270o
360o
角α的弧度数
sinα
cosα
tanα
1
2
3
2
3
3
2
2
2
2
1
3
2
1
2
3
1
0
0
0
0
-1
-1
1
0
0
1.
角α的终边经过点P(0,
b)则(
)
A.sin
α=0
B.sin
α=1
C.sin
α=-1
D.sin
α=±1
D
2.若角600o的终边上有一点(-4,
a),则a的值是(
)
600o的终边落在第三象限,∴a<0,
60°
3.已知角α的终边经过点P(2a,-3a),求角α的正弦、余弦、正切值.
x
=2a,
y
=
-3a
r=
=
=
x2+y2
(2a)2+(-3a)2
a
13
当a<0时,sinα=
,cosα=-
,
tanα=-
3
13
13
3
2
2
13
13
当a>0时,sinα=-
,cosα=
tanα=-
3
13
13
2
13
13
3
2
4.已知角的终边落在直线y=2x上,求sinα、c
osα、tanα的值.
[解析] 当角的终边在第一象限时,在角的终边上取点P(1,2),
(
)
(
)
三角函数在各象限内的符号:
y
x
o
y
x
o
y
x
o
+
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
+
-
-
+
+
-
-
+
+
-
-
例3
确定下列三角函数值的符号:
(1)
(2)
(3)
(1)因为250°是第三象限角,所以cosα<0;
解:
(2)∵-672?=-2×360?+48?,∴tan(-672?)>0.
π
4
(3)因为-
是第四象限角,所以
π
4
sin(-
)<0
探究
根据三角函数的定义:
终边相同的角的同一三角函数值是否相等?
∵终边相同的角的集合为:
终边相同
点的坐标相同
三角函数值相同
终边相同的角的三角函数关系
终边相同的角的同一三角函数值相等,由此得到一组公式(公式一):
(其中
)
利用公式一,作用在于可将求任意角的三角函数值,转化为求0~2π
(或0°~360°)范围内的三角函数值.
(1)
cos390°=cos(360°+30°)=cos30°=
3
2
(2)
7π
4
sin(-
)=sin(-2π+
)=sin
=
π
4
π
4
2
2
(3)tan(-675°)=tan(-2×360°+45°)=tan45°=1
(4)tan3π=tan(2π+π)=tanπ=0
C
2.已知角α的终边经过点(3a-9,a+2),且cosα≤0,sinα>0,则a的取值范围是____________
(-2,3]
3a-9≤0
a+2>0
归纳
总结
1.
内容总结:
①三角函数的概念.
②三角函数的定义域及三角函数值在各象限的符号.
③诱导公式一.
2
.方法总结:
运用了定义法、公式法、数形结合法解题.
3
.体现的数学思想:
划归的思想,数形结合的思想.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
