高中数学_空间中直线与直线之间的位置关系教案。学案
文档属性
| 名称 | 高中数学_空间中直线与直线之间的位置关系教案。学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 39.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-08-12 00:00:00 | ||
图片预览

文档简介
§2.1.2 空间直线与直线之间的位置关系
三维目标:
正确理解空间直线与直线的位置关系,特别是两异面直线的异面关系。
以公理4和等角定理为基础,正确理解两异面直线所成的角的概念及它们的应用。
进一步培养学生的空间想象能力,以及有根有据、实事求是等严肃的科学态度和品质。
重点:
两直线异面的判定方法,以及两异面直线所成角的求法。
难点:
两异面直线所成角的求法。
<自学导读>:
什么叫做异面直线?
总结空间中直线与直线的位置关系。
两异面直线的画法。
在同一平面内,如果两直线都与第三条直线平行,那么这两条直线互相平行,在空间这个结论成立吗?
什么是空间等角定理?
什么叫做两异面直线所成的角?
什么叫做两直线互相垂直?
<预习自测>
在平面中,两直线的位置关系有 、 。
我们把 叫做异面直线。
空间两直线位置关系
4、例1: 如右图,正方体ABCD-A1B1C1D1中
与A1B异面的棱有 条,哪几条? 。
5、公理4: 。
6、定理: 。
7、两异面直线a与b所成角的范围 。
8、两直线垂直可分为 和 。
<教学过程>
异面直线
定义:不同在任何一个平面内的两条直线。
判断正误:①若l1,l2,则l1、l2为异面直线。( )
②若l1与l2相交,l2与l3相交,则l1与l3相交。( )
明确: 。
异面直线的直观表示:
平行线公理
公理4:平行于同一条直线的两条直线互相平行。
问:拿一本书张开封面,要证明书面的两边
边缘AB∥CD,该怎么办?
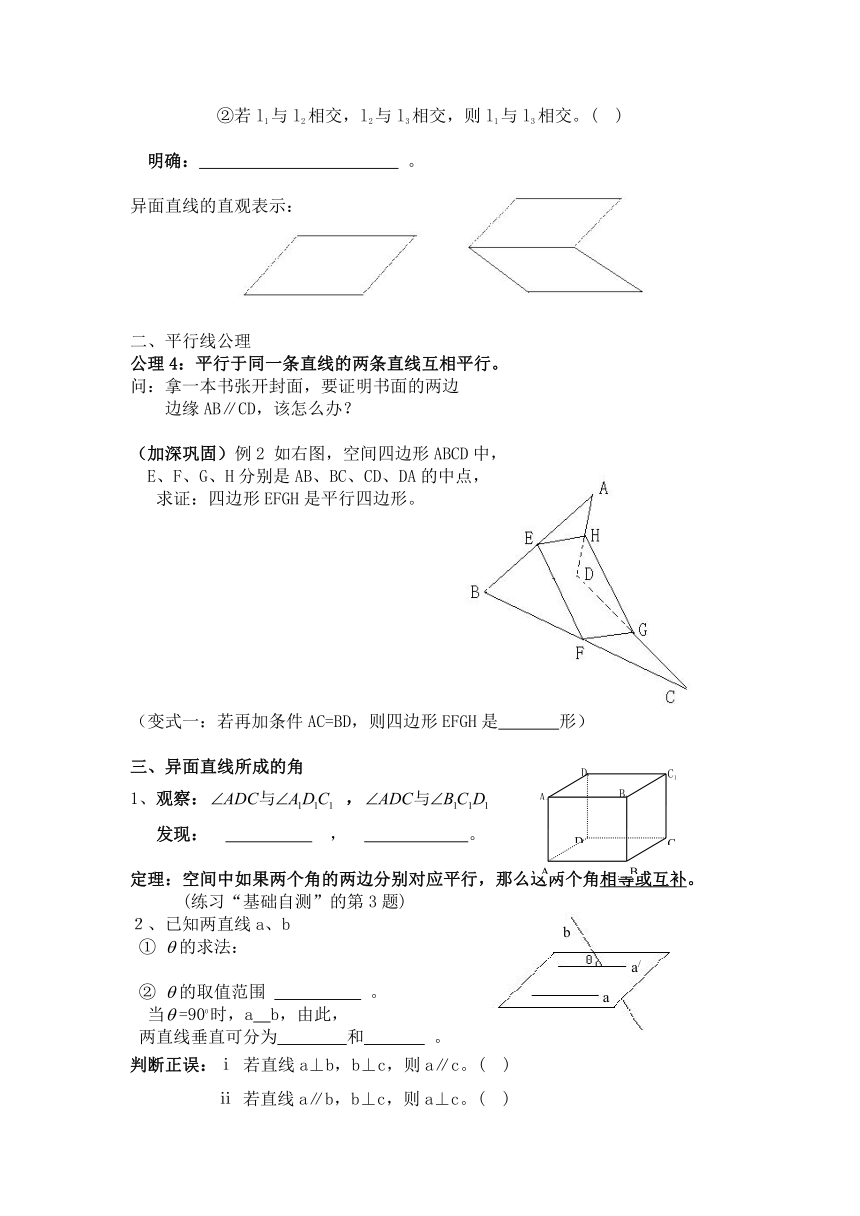
(加深巩固)例2 如右图,空间四边形ABCD中,
E、F、G、H分别是AB、BC、CD、DA的中点,
求证:四边形EFGH是平行四边形。
(变式一:若再加条件AC=BD,则四边形EFGH是 形)
三、异面直线所成的角
观察: ,
发现: , 。
定理:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补。
(练习“基础自测”的第3题)
2、已知两直线a、b
① 的求法:
② 的取值范围 。
当=900时,a b,由此,
两直线垂直可分为 和 。
判断正误:ⅰ 若直线a⊥b,b⊥c,则a∥c。( )
ⅱ 若直线a∥b,b⊥c,则a⊥c。( )
例2 变式二:若再加条件AC⊥BD,则四边形EFGH是 形。
变式三:若再加条件AC=BD,且AC⊥BD,则四边形EFGH是 形。
(预习书上例3,完成下面练习)
练习: 1、已知正方体ABCD-A1B1C1D1
(1)证明: AA1⊥C1D1
(2)求异面直线BC与B1D1所成角的度数。
(3)求异面直线A1C1与D1C所成角的度数
(拓展提高)如右图,点A是BCD所在平面外一点,AD=BC=2,E、F分别是AB、CD的中点,且EF=,求异面直线AD与BC所成的角。
<课堂小结>
本节知识回顾与总结:
巩固练习
一、基础自测
1、以下命题正确的是 ( )
①若直线a、b异面,b、c异面,则a、c异面。
②若直线a、b相交,b、c相交,则a、c相交。
③若直线a⊥b,b⊥c,则a∥c。 ④若直线a∥b,b⊥c,则a⊥c。
A、①④ B、③④ C、④ D、②④
2、若直线a⊥b,则a与b ( )
A、一定相交 B、一定是共面 C、一定是异面 D、一定不平行
3、空间两个角,的两边对应平行,且=600则为 ( )
A、600 B、1200 C、300 D、600或1200
4、空间四边形的对角线互相垂直且相等,顺次连接这个四边形各边中点,所组成的四边形是 ( )
A、梯形 B、矩形 C、平行四边形 D、正方形
5、空间四边形ABCD中,AB、BC、CD的中点分别是P、Q、R,且PQ=2,QR=,PR=3,那么异面直线AC和BD所成的角是 ( )
A、900 B、300 C、450 D、600
二、拓展提高
1、右图是一个正方体的展开图,在原正方体中
有下列命题,期中正确命题的序号是 ( )
①AB与CD所在的直线垂直
②CD与EF所在的直线平行
③AB与MN所在直线成600角
④MN与EF所在直线异面
A、①③ B、①④
C、②③ D、③④
D1
A1
B1
C1
C
D
A
B
C1
D1
B11
A1
C
D
B
B
A
b
a/
a
C1
B1
D
A1
A
D1
C
B
三维目标:
正确理解空间直线与直线的位置关系,特别是两异面直线的异面关系。
以公理4和等角定理为基础,正确理解两异面直线所成的角的概念及它们的应用。
进一步培养学生的空间想象能力,以及有根有据、实事求是等严肃的科学态度和品质。
重点:
两直线异面的判定方法,以及两异面直线所成角的求法。
难点:
两异面直线所成角的求法。
<自学导读>:
什么叫做异面直线?
总结空间中直线与直线的位置关系。
两异面直线的画法。
在同一平面内,如果两直线都与第三条直线平行,那么这两条直线互相平行,在空间这个结论成立吗?
什么是空间等角定理?
什么叫做两异面直线所成的角?
什么叫做两直线互相垂直?
<预习自测>
在平面中,两直线的位置关系有 、 。
我们把 叫做异面直线。
空间两直线位置关系
4、例1: 如右图,正方体ABCD-A1B1C1D1中
与A1B异面的棱有 条,哪几条? 。
5、公理4: 。
6、定理: 。
7、两异面直线a与b所成角的范围 。
8、两直线垂直可分为 和 。
<教学过程>
异面直线
定义:不同在任何一个平面内的两条直线。
判断正误:①若l1,l2,则l1、l2为异面直线。( )
②若l1与l2相交,l2与l3相交,则l1与l3相交。( )
明确: 。
异面直线的直观表示:
平行线公理
公理4:平行于同一条直线的两条直线互相平行。
问:拿一本书张开封面,要证明书面的两边
边缘AB∥CD,该怎么办?
(加深巩固)例2 如右图,空间四边形ABCD中,
E、F、G、H分别是AB、BC、CD、DA的中点,
求证:四边形EFGH是平行四边形。
(变式一:若再加条件AC=BD,则四边形EFGH是 形)
三、异面直线所成的角
观察: ,
发现: , 。
定理:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补。
(练习“基础自测”的第3题)
2、已知两直线a、b
① 的求法:
② 的取值范围 。
当=900时,a b,由此,
两直线垂直可分为 和 。
判断正误:ⅰ 若直线a⊥b,b⊥c,则a∥c。( )
ⅱ 若直线a∥b,b⊥c,则a⊥c。( )
例2 变式二:若再加条件AC⊥BD,则四边形EFGH是 形。
变式三:若再加条件AC=BD,且AC⊥BD,则四边形EFGH是 形。
(预习书上例3,完成下面练习)
练习: 1、已知正方体ABCD-A1B1C1D1
(1)证明: AA1⊥C1D1
(2)求异面直线BC与B1D1所成角的度数。
(3)求异面直线A1C1与D1C所成角的度数
(拓展提高)如右图,点A是BCD所在平面外一点,AD=BC=2,E、F分别是AB、CD的中点,且EF=,求异面直线AD与BC所成的角。
<课堂小结>
本节知识回顾与总结:
巩固练习
一、基础自测
1、以下命题正确的是 ( )
①若直线a、b异面,b、c异面,则a、c异面。
②若直线a、b相交,b、c相交,则a、c相交。
③若直线a⊥b,b⊥c,则a∥c。 ④若直线a∥b,b⊥c,则a⊥c。
A、①④ B、③④ C、④ D、②④
2、若直线a⊥b,则a与b ( )
A、一定相交 B、一定是共面 C、一定是异面 D、一定不平行
3、空间两个角,的两边对应平行,且=600则为 ( )
A、600 B、1200 C、300 D、600或1200
4、空间四边形的对角线互相垂直且相等,顺次连接这个四边形各边中点,所组成的四边形是 ( )
A、梯形 B、矩形 C、平行四边形 D、正方形
5、空间四边形ABCD中,AB、BC、CD的中点分别是P、Q、R,且PQ=2,QR=,PR=3,那么异面直线AC和BD所成的角是 ( )
A、900 B、300 C、450 D、600
二、拓展提高
1、右图是一个正方体的展开图,在原正方体中
有下列命题,期中正确命题的序号是 ( )
①AB与CD所在的直线垂直
②CD与EF所在的直线平行
③AB与MN所在直线成600角
④MN与EF所在直线异面
A、①③ B、①④
C、②③ D、③④
D1
A1
B1
C1
C
D
A
B
C1
D1
B11
A1
C
D
B
B
A
b
a/
a
C1
B1
D
A1
A
D1
C
B
