8.3.2.2球的体积和表面积课件-2020-2021学年高一下学期数学人教A版(2019)必修第二册(共12张PPT)
文档属性
| 名称 | 8.3.2.2球的体积和表面积课件-2020-2021学年高一下学期数学人教A版(2019)必修第二册(共12张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 11.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-28 22:52:12 | ||
图片预览


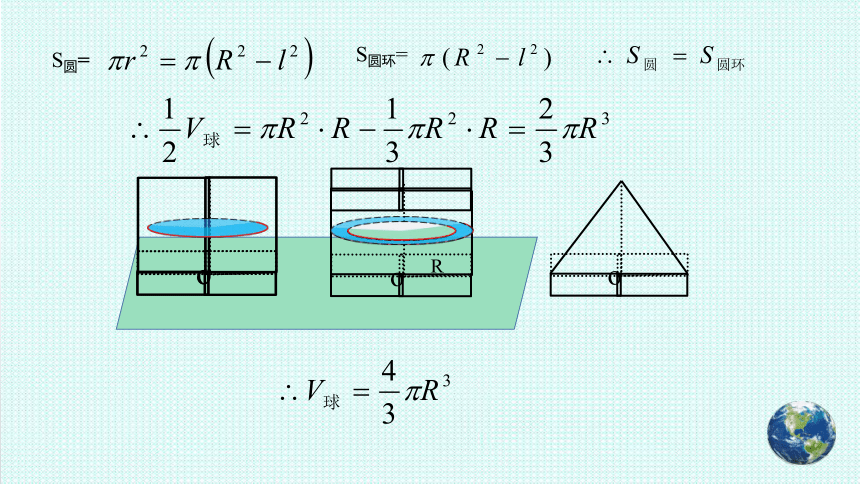


文档简介
(共12张PPT)
球的体积和表面积
安徽淮南第四中学
2021.4
曹冲称象
乌鸦喝水
实验:排液法测小球的体积.
r
h
小球的体积等于它排开液体的体积
V球=πr2(H-h)
H
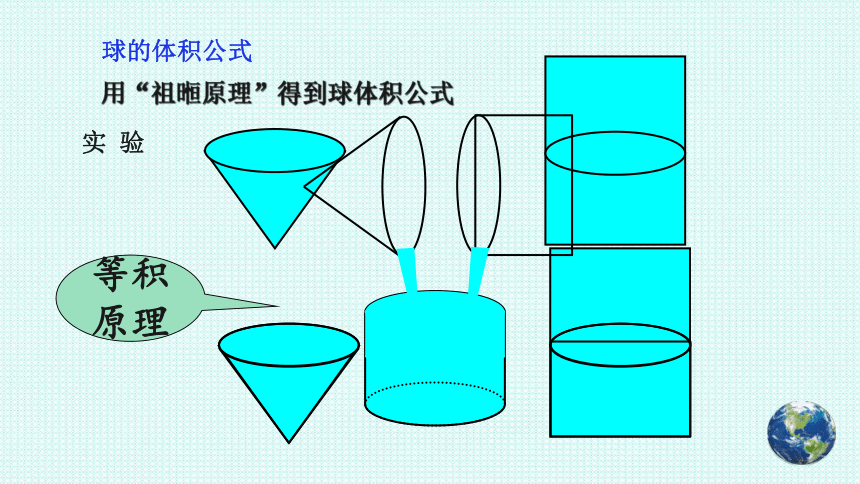
球的体积公式
用“祖暅原理”得到球体积公式
实
验
等积
原理
S圆=
S圆环=
球的表面积公式
类比“圆的面积”的推导,来探究“球的表面积”的推导?(刘徽的“割圆术”)
O
R
近似三角形,底长
第一步:分割
(1)球面被分割成n个网格,球的表面分成了n个“小棱锥”的底面;
O
(2)如果网格分的越细,“小棱锥”的底面近似平面,高近似于球的半径R.
第二步:求近似和
设“小锥体”的体积为:
第三步:转化为球的表面积
球的性质
性质1:用一个平面去截球,截面是圆面;用一个平面去截球面,
截线是圆.
球面被经过球心的平面截得的圆叫做大圆.
球面被不过球心的截面截得的圆叫球的小圆.
性质2:
球心和截面圆心的连线垂直于截面.
性质3:
球心到截面的距离d与球
的半径R及截面的半径r
有下面的关系:
O
O1
例1.
如图,某种浮标由两个半球和一个圆柱黏合而成,半球的直径是0.3m,圆柱高0.6m.如果在浮标表面涂一层防水漆,每平方米需要0.5kg涂料,那么给1000个这样的浮标涂防水漆需要多少涂料?(x取3.14)
解:一个浮标的表面积为2π×0.15×0.6+4π×0.152=0.8478(m2),
所以给1000个这样的浮标涂防水漆约需涂料
0.8478×0.5×1000=423.9(kg).
例2.用与球心的距离为1的平面去截球,所得的截面积为π,求这个球的体积与表面积.
解:由题意得球心到截面圆的距离为1,
又S截=πr2=π,得r=1.即截面圆的半径r=1.
O
O1
r
R
已知过球面上三点A、B、C的截面到球心的距离等于球半径的一半,且AC=BC=6,AB=4,求球的表面积与球的体积.
先求截面圆的半径r
A
B
C
b2+c2-a2
2bc
cos
A=
cos
A=
1
3
sinA=
3
2
截面圆的半径r=
2
9
球半径R=
3
S球=54π
V球=27
π
已知球的半径为
10
cm,若它的一个截面圆的面积是36π
cm2,则球心与截面圆周圆心的距离是______.
8
cm
A
B
O
例3.如图所示,一个圆锥形的空杯子上放着一个直径为8
cm的半球形的冰淇淋,请你设计一种这样的圆锥形杯子(杯口直径等于半球形的冰淇淋的直径,杯子壁厚忽略不计),使冰淇淋融化后不会溢出杯子,怎样设计最省材料?材料最省为多少?
解 要使冰淇淋融化后不会溢出杯子,则必须有V圆锥≥V半球,
球的体积和表面积
安徽淮南第四中学
2021.4
曹冲称象
乌鸦喝水
实验:排液法测小球的体积.
r
h
小球的体积等于它排开液体的体积
V球=πr2(H-h)
H
球的体积公式
用“祖暅原理”得到球体积公式
实
验
等积
原理
S圆=
S圆环=
球的表面积公式
类比“圆的面积”的推导,来探究“球的表面积”的推导?(刘徽的“割圆术”)
O
R
近似三角形,底长
第一步:分割
(1)球面被分割成n个网格,球的表面分成了n个“小棱锥”的底面;
O
(2)如果网格分的越细,“小棱锥”的底面近似平面,高近似于球的半径R.
第二步:求近似和
设“小锥体”的体积为:
第三步:转化为球的表面积
球的性质
性质1:用一个平面去截球,截面是圆面;用一个平面去截球面,
截线是圆.
球面被经过球心的平面截得的圆叫做大圆.
球面被不过球心的截面截得的圆叫球的小圆.
性质2:
球心和截面圆心的连线垂直于截面.
性质3:
球心到截面的距离d与球
的半径R及截面的半径r
有下面的关系:
O
O1
例1.
如图,某种浮标由两个半球和一个圆柱黏合而成,半球的直径是0.3m,圆柱高0.6m.如果在浮标表面涂一层防水漆,每平方米需要0.5kg涂料,那么给1000个这样的浮标涂防水漆需要多少涂料?(x取3.14)
解:一个浮标的表面积为2π×0.15×0.6+4π×0.152=0.8478(m2),
所以给1000个这样的浮标涂防水漆约需涂料
0.8478×0.5×1000=423.9(kg).
例2.用与球心的距离为1的平面去截球,所得的截面积为π,求这个球的体积与表面积.
解:由题意得球心到截面圆的距离为1,
又S截=πr2=π,得r=1.即截面圆的半径r=1.
O
O1
r
R
已知过球面上三点A、B、C的截面到球心的距离等于球半径的一半,且AC=BC=6,AB=4,求球的表面积与球的体积.
先求截面圆的半径r
A
B
C
b2+c2-a2
2bc
cos
A=
cos
A=
1
3
sinA=
3
2
截面圆的半径r=
2
9
球半径R=
3
S球=54π
V球=27
π
已知球的半径为
10
cm,若它的一个截面圆的面积是36π
cm2,则球心与截面圆周圆心的距离是______.
8
cm
A
B
O
例3.如图所示,一个圆锥形的空杯子上放着一个直径为8
cm的半球形的冰淇淋,请你设计一种这样的圆锥形杯子(杯口直径等于半球形的冰淇淋的直径,杯子壁厚忽略不计),使冰淇淋融化后不会溢出杯子,怎样设计最省材料?材料最省为多少?
解 要使冰淇淋融化后不会溢出杯子,则必须有V圆锥≥V半球,
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
