湘教版七年级上册数学 第3章3.4.4用一元一次方程解行程问题 课件(37张PPT)
文档属性
| 名称 | 湘教版七年级上册数学 第3章3.4.4用一元一次方程解行程问题 课件(37张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-29 14:02:29 | ||
图片预览









文档简介
(共37张PPT)
第4节
一元一次方程模型的应用
第三章
一元一次方程
第4课时
用一元一次方程解行程问题
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
一般行程问题
顺流(风)、逆流(风)问题
上坡、下坡问题
课时导入
复习提问
引出问题
复习提问
引出问题
一架飞机在两城之间飞行,顺风需要4小时,逆风需要4.5小时;求飞机在两城之间往返的平均速度.该如何做呢?
知识点
一般行程问题
知1-导
感悟新知
1
甲、乙两地间的路程为375
km.一辆轿车和一辆公共汽车分别从甲、乙两地同时出发沿公路相向而行,轿车的平均速度为90
km/h,公共汽车的平均速度为60
km/h.它们出发后多少小时在
途中相遇?
知1-导
感悟新知
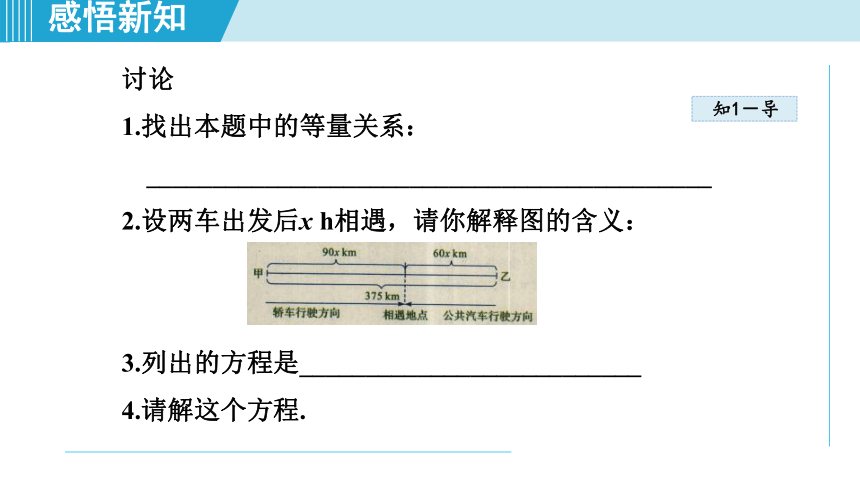
讨论
1.找出本题中的等量关系:
___________________________________________
2.设两车出发后x
h相遇,请你解释图的含义:
3.列出的方程是__________________________
4.请解这个方程.
知1-导
总
结
感悟新知
1.行程问题的基本关系式:路程=速度×时间,时间=路程+速度,速度=路程+时间.
2.行程问题中的等量关系:
(1)相遇问题中的等量关系:
①甲走的路程+乙走的路程=甲、乙出发点之间的路程;
②若甲、乙同时出发,甲用的时间=乙用的时间,
知1-导
总
结
感悟新知
(2)追及问题中的等量关系:
①快者走的路程-慢者走的路程=追及路程;
②若同时出发,快者追上慢者时,快者用的时间=慢者用的时间.
知1-导
感悟新知
特别提醒
1.
在行程问题的三个量(路程、速度、时间)中,一个量已知,另一个量设元,则第三个量用来列方程.
2.
在相遇和追及问题中,若两者同时出发,则时间相等,利用两者路程之间的关系列方程.
3.
航行问题中涉及顺和逆的问题,只要路线相同,则路程不变.
知1-讲
感悟新知
例
1
小明与小红的家相距20
km,小明从家里出发骑自行车去小红家,两人商定小红到时候从家里出发骑自行车去接小明,已知小明骑车的速度为13
km/h,小红骑车的速度是12
km/h.
(1)如果两人同时出发,那么他们经过多少小时相遇?
(2)如果小明先走30
min,那么小红骑车要走多少小时才能与小明相遇?
知1-练
感悟新知
分析:由于小明与小红都从家里出发,相向而行,所以相遇时,他们走的路程的和等于两家之间的距离.不管两人是同时出发,还是有一人先走,都有小明走的路程+小红走的路程=两家之间的距离(20
km).
知1-练
感悟新知
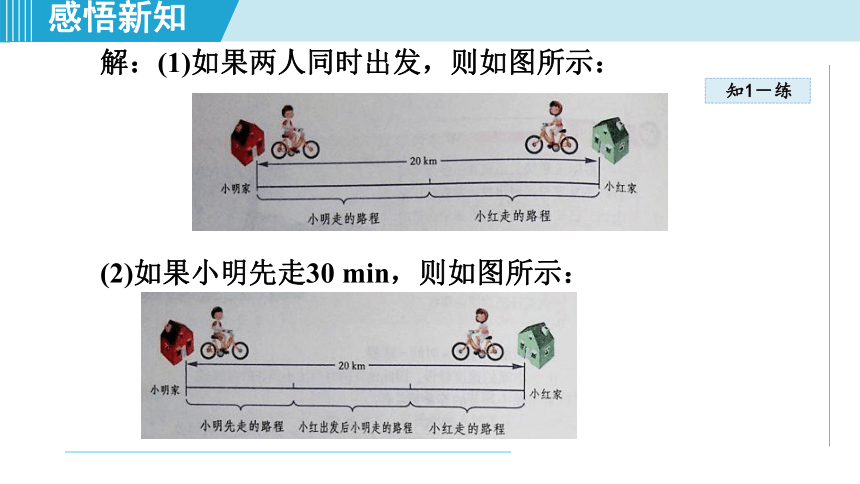
解:(1)如果两人同时出发,则如图所示:
(2)如果小明先走30
min,则如图所示:
知1-练
感悟新知
解:(1)设小明与小红骑车走了xh后相遇,则根据等量关系,得13x+12x=20.
解得x=0.8.
(2)设小红骑车走了th后与小明相遇,则根据等量关系,得13(0.5+t)+
12t=20.
解得t=0.54.
答:(1)经过0.8h他们两人相遇;(2)小红骑车走0.54h后与小明相遇.
知1-讲
总
结
感悟新知
(1)行程问题中,分析时,可借助图示、列表来分析数量关系,图示可直观地找出路程等量关系,列表可将路程、速度、时间的关系清晰地展示出来.
知1-讲
总
结
感悟新知
(2)本例是求时间,可设时间为未知数,从表中求路程;如果要求的是路程,那么可设路程为未知数,从表中求时间,其依据是路程、速度和时间三者间的关系式,如(2)题若将“几小时后两车相遇?"改为“相遇时快车走了多少干米?"如间接设未知数,则原导引及解不变,仅只将求出后,再求出90x的值即可,如直接设未知数,则导引改为:
列表:
等量关系:慢车行驶时间-
h=快车行驶时间.
方程为:
知1-讲
总
结
感悟新知
路程(km)
速度(km/h)
时间(h)
慢车
1500-x
60
快车
x
90
知1-讲
总
结
感悟新知
(3)一般规律:在路程、速度、时间这三个量中,甲量已知,从乙量设元,则从丙量中找相等关系列方程;在所有行程问题中,一般都已知一个量,另两个量相互之间都存在相等关系.
1.汽车以72千米/时的速度在公路上行驶,开向寂静的山谷,驾驶员摁一下喇叭,4秒后听到回声,这时汽车离山谷多远?已知空气中声音的传播速度约为340米/秒,设听到回声时,汽车离山谷x米,根据题意,列出方程为( )
A.2x+4×20=4×340
B.2x-4×72=4×340
C.2x+4×72=4×340
D.2x-4×20=4×340
知1-练
感悟新知
A
2.甲、乙两人相距10千米,甲先出发1小时后乙再出发,甲在乙后面,二人同向而行,已知甲每小时走5千米,乙每小时走4千米,问乙出发后几小时被甲追上?
知1-练
感悟新知
解析:如果设乙出发×小时候被追上,利用线段图分析题意,如图所示.甲走的路程-乙走的路程=10千米.
知1-练
感悟新知
解:设乙出发后x小时被甲追上,
依题意得5(x+1)-4x=10,解得x=5.
答:乙出发后5小时被甲追上.
知2-导
感悟新知
知识点
顺流(风)、逆流(风)问题
2
航行问题中的基本关系式:
顺水(风)速度=静水(风)速度+水(风)速度.
逆水(风)速度=静水(风)速度-水(风)速度.
知2-讲
感悟新知
例2
一架飞机飞行在两个城市之间,凤速为24km/h,顺风飞行需要2
h
50
min,逆风飞行需要3h,求飞机在无风时的平均速度及两城市之间的距离
知2-讲
感悟新知
方法一:设速度为未知数。
导引:
设飞机在无风时的平均速度为xkm/h,2h
50
min=
h.
列表:
等量关系:顺风飞行路程=逆风飞行路程.
路程(km)
速度(km/h)
时间(h)
顺风飞行
x+24
逆风飞行
3(x-24)
x-24
3
知2-讲
感悟新知
解:2
h
50
min
=h.
设飞机在无风时的平均速度为x
km/h,则顺风速度为(x
+24)km/h,逆风速度为(x-24)km/h,根据题意,得
(x+24)=3(x-24).解得x=840.
3(x-24)=2
448.
答:飞机在无凤时的平均速度为840
km/h,两城市之间的距离是2
448
km.
知2-讲
感悟新知
方法二:设路程为未知数。
导引:
设两个城市之间的距离为ykm/h,2h
50
min=
h.
列表:
等量关系:顺凤飞行速度-风速=逆风飞行速度+凤速.即;无凤时速度相等.
路程(km)
速度(km/h)
时间(h)
顺风飞行
y
逆风飞行
y
3
知2-讲
感悟新知
解:设两城市之间的距离为y
km,则顺风飞行的速度为
km/h,逆风飞行的速度为
km/h
,
根据题意,得:
解得:y
=
2
448.所以
答:飞机在无风时的平均速度为840
km/h
,两城市之间的距离为2448
km.,
知2-讲
感悟新知
总
结
(1)行程问题:虽然不同的问题有不同的关系式,但列表格分析的方式是一致的,在路程、速度、时间这三个量中,已知量是一致的,设的未知量不同,所列方程也不同.
知2-讲
感悟新知
总
结
(2)解有关行程问题时,始终要记住一句话:在行程问题三个基本量(路程、速度、时间)中:①如果速度已知,若从时间设元,则从路程找等量关系列方程;若从路程设元,则从时间找等量关系列方程;②如果时间已知,若从速度设元,则从路程找等量关系列方程;若从路程设元,则从速度找等量关系列方程;③如果路程已知,若从时间(或速度)设元,则从速度(或时间)找等量关系列方程.
知2-练
感悟新知
1.有一架战斗机的贮油量最多够它在空中飞行4.6
h,这架战斗机出航时顺风飞行,在无风时的速度是575
km/h,风速为25
km/h,这架战斗机最远飞出多少千米就应返航?
知2-练
感悟新知
解:设这架战斗机顺风飞行的时间为t
h.
依题意,得(575+25)t=(575-25)(4.6-t).
解得t=2.2.
则(575+25)t=600×2.2=1
320.
故这架战斗机最远飞出1
320
km就应返航.
知3-讲
感悟新知
知识点
上坡、下坡问题
3
小明从家去外婆家,去时是上坡,每小时行12千米,回来时是下坡,每小时行18千米,来回共用了5小时,求小明家到外婆家的距离.
例
3
知3-讲
感悟新知
解:设小明家到外婆家的距离是x千米,
由题意得:
解得:x=36
答:小明家到外婆家的距离是36千米.
知3-讲
感悟新知
总
结
根据找出等量关系是解答问题的关键.
知3-练
感悟新知
1.家住山脚下的孔明同学想从家出发去登山游玩,据以往的经验,他获得如下信息:
(1)他下山时的速度比上山时的速度每时快1千米;
(2)他上山2时到达的位置,离山顶还有1千米;
(3)抄近路下山,下山路程比上山路程近2千米;
(4)下山用1时.
知3-练
感悟新知
根据上面的信息,他作出如下计划:
(1)在山顶游览1时;
(2)中午12:00回到家吃午餐.
若依据以上信息和计划登山游玩,请问:孔明同学应该在什么时间从家出发?
知3-练
感悟新知
解:设上山的速度为v千米/时,
则下山的速度为(v+1)千米/时,
由题意得2v+1=v+1+2,解得v=2.
即上山的速度是2千米/时,下山的速度是3千米/时.
故上山用的时间为2+1÷2=2.5(时).
所以共用时间为2.5+1+1=4.5(时),
所以出发时间为12:00-4时30分=7:30.
故孔明同学应该在7:30从家出发.
课堂小结
用一元一次方程解行程问题
行程问题有相遇问题,追及问题,顺流、逆流问题,上坡、下坡问题等.在运动形式上分直线运动及曲线运动(如环形跑道).相遇问题是相向而行,相遇时的总路程为两运动物体的路程和.追及问题是同向而行,分慢的在快的前面或慢的先行若干时间,快的再追.顺流、逆流、顺风、逆风、上下坡等问题应注意运动方向.
必做:
请完成教材课后习题
课后作业
作业
第4节
一元一次方程模型的应用
第三章
一元一次方程
第4课时
用一元一次方程解行程问题
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
一般行程问题
顺流(风)、逆流(风)问题
上坡、下坡问题
课时导入
复习提问
引出问题
复习提问
引出问题
一架飞机在两城之间飞行,顺风需要4小时,逆风需要4.5小时;求飞机在两城之间往返的平均速度.该如何做呢?
知识点
一般行程问题
知1-导
感悟新知
1
甲、乙两地间的路程为375
km.一辆轿车和一辆公共汽车分别从甲、乙两地同时出发沿公路相向而行,轿车的平均速度为90
km/h,公共汽车的平均速度为60
km/h.它们出发后多少小时在
途中相遇?
知1-导
感悟新知
讨论
1.找出本题中的等量关系:
___________________________________________
2.设两车出发后x
h相遇,请你解释图的含义:
3.列出的方程是__________________________
4.请解这个方程.
知1-导
总
结
感悟新知
1.行程问题的基本关系式:路程=速度×时间,时间=路程+速度,速度=路程+时间.
2.行程问题中的等量关系:
(1)相遇问题中的等量关系:
①甲走的路程+乙走的路程=甲、乙出发点之间的路程;
②若甲、乙同时出发,甲用的时间=乙用的时间,
知1-导
总
结
感悟新知
(2)追及问题中的等量关系:
①快者走的路程-慢者走的路程=追及路程;
②若同时出发,快者追上慢者时,快者用的时间=慢者用的时间.
知1-导
感悟新知
特别提醒
1.
在行程问题的三个量(路程、速度、时间)中,一个量已知,另一个量设元,则第三个量用来列方程.
2.
在相遇和追及问题中,若两者同时出发,则时间相等,利用两者路程之间的关系列方程.
3.
航行问题中涉及顺和逆的问题,只要路线相同,则路程不变.
知1-讲
感悟新知
例
1
小明与小红的家相距20
km,小明从家里出发骑自行车去小红家,两人商定小红到时候从家里出发骑自行车去接小明,已知小明骑车的速度为13
km/h,小红骑车的速度是12
km/h.
(1)如果两人同时出发,那么他们经过多少小时相遇?
(2)如果小明先走30
min,那么小红骑车要走多少小时才能与小明相遇?
知1-练
感悟新知
分析:由于小明与小红都从家里出发,相向而行,所以相遇时,他们走的路程的和等于两家之间的距离.不管两人是同时出发,还是有一人先走,都有小明走的路程+小红走的路程=两家之间的距离(20
km).
知1-练
感悟新知
解:(1)如果两人同时出发,则如图所示:
(2)如果小明先走30
min,则如图所示:
知1-练
感悟新知
解:(1)设小明与小红骑车走了xh后相遇,则根据等量关系,得13x+12x=20.
解得x=0.8.
(2)设小红骑车走了th后与小明相遇,则根据等量关系,得13(0.5+t)+
12t=20.
解得t=0.54.
答:(1)经过0.8h他们两人相遇;(2)小红骑车走0.54h后与小明相遇.
知1-讲
总
结
感悟新知
(1)行程问题中,分析时,可借助图示、列表来分析数量关系,图示可直观地找出路程等量关系,列表可将路程、速度、时间的关系清晰地展示出来.
知1-讲
总
结
感悟新知
(2)本例是求时间,可设时间为未知数,从表中求路程;如果要求的是路程,那么可设路程为未知数,从表中求时间,其依据是路程、速度和时间三者间的关系式,如(2)题若将“几小时后两车相遇?"改为“相遇时快车走了多少干米?"如间接设未知数,则原导引及解不变,仅只将求出后,再求出90x的值即可,如直接设未知数,则导引改为:
列表:
等量关系:慢车行驶时间-
h=快车行驶时间.
方程为:
知1-讲
总
结
感悟新知
路程(km)
速度(km/h)
时间(h)
慢车
1500-x
60
快车
x
90
知1-讲
总
结
感悟新知
(3)一般规律:在路程、速度、时间这三个量中,甲量已知,从乙量设元,则从丙量中找相等关系列方程;在所有行程问题中,一般都已知一个量,另两个量相互之间都存在相等关系.
1.汽车以72千米/时的速度在公路上行驶,开向寂静的山谷,驾驶员摁一下喇叭,4秒后听到回声,这时汽车离山谷多远?已知空气中声音的传播速度约为340米/秒,设听到回声时,汽车离山谷x米,根据题意,列出方程为( )
A.2x+4×20=4×340
B.2x-4×72=4×340
C.2x+4×72=4×340
D.2x-4×20=4×340
知1-练
感悟新知
A
2.甲、乙两人相距10千米,甲先出发1小时后乙再出发,甲在乙后面,二人同向而行,已知甲每小时走5千米,乙每小时走4千米,问乙出发后几小时被甲追上?
知1-练
感悟新知
解析:如果设乙出发×小时候被追上,利用线段图分析题意,如图所示.甲走的路程-乙走的路程=10千米.
知1-练
感悟新知
解:设乙出发后x小时被甲追上,
依题意得5(x+1)-4x=10,解得x=5.
答:乙出发后5小时被甲追上.
知2-导
感悟新知
知识点
顺流(风)、逆流(风)问题
2
航行问题中的基本关系式:
顺水(风)速度=静水(风)速度+水(风)速度.
逆水(风)速度=静水(风)速度-水(风)速度.
知2-讲
感悟新知
例2
一架飞机飞行在两个城市之间,凤速为24km/h,顺风飞行需要2
h
50
min,逆风飞行需要3h,求飞机在无风时的平均速度及两城市之间的距离
知2-讲
感悟新知
方法一:设速度为未知数。
导引:
设飞机在无风时的平均速度为xkm/h,2h
50
min=
h.
列表:
等量关系:顺风飞行路程=逆风飞行路程.
路程(km)
速度(km/h)
时间(h)
顺风飞行
x+24
逆风飞行
3(x-24)
x-24
3
知2-讲
感悟新知
解:2
h
50
min
=h.
设飞机在无风时的平均速度为x
km/h,则顺风速度为(x
+24)km/h,逆风速度为(x-24)km/h,根据题意,得
(x+24)=3(x-24).解得x=840.
3(x-24)=2
448.
答:飞机在无凤时的平均速度为840
km/h,两城市之间的距离是2
448
km.
知2-讲
感悟新知
方法二:设路程为未知数。
导引:
设两个城市之间的距离为ykm/h,2h
50
min=
h.
列表:
等量关系:顺凤飞行速度-风速=逆风飞行速度+凤速.即;无凤时速度相等.
路程(km)
速度(km/h)
时间(h)
顺风飞行
y
逆风飞行
y
3
知2-讲
感悟新知
解:设两城市之间的距离为y
km,则顺风飞行的速度为
km/h,逆风飞行的速度为
km/h
,
根据题意,得:
解得:y
=
2
448.所以
答:飞机在无风时的平均速度为840
km/h
,两城市之间的距离为2448
km.,
知2-讲
感悟新知
总
结
(1)行程问题:虽然不同的问题有不同的关系式,但列表格分析的方式是一致的,在路程、速度、时间这三个量中,已知量是一致的,设的未知量不同,所列方程也不同.
知2-讲
感悟新知
总
结
(2)解有关行程问题时,始终要记住一句话:在行程问题三个基本量(路程、速度、时间)中:①如果速度已知,若从时间设元,则从路程找等量关系列方程;若从路程设元,则从时间找等量关系列方程;②如果时间已知,若从速度设元,则从路程找等量关系列方程;若从路程设元,则从速度找等量关系列方程;③如果路程已知,若从时间(或速度)设元,则从速度(或时间)找等量关系列方程.
知2-练
感悟新知
1.有一架战斗机的贮油量最多够它在空中飞行4.6
h,这架战斗机出航时顺风飞行,在无风时的速度是575
km/h,风速为25
km/h,这架战斗机最远飞出多少千米就应返航?
知2-练
感悟新知
解:设这架战斗机顺风飞行的时间为t
h.
依题意,得(575+25)t=(575-25)(4.6-t).
解得t=2.2.
则(575+25)t=600×2.2=1
320.
故这架战斗机最远飞出1
320
km就应返航.
知3-讲
感悟新知
知识点
上坡、下坡问题
3
小明从家去外婆家,去时是上坡,每小时行12千米,回来时是下坡,每小时行18千米,来回共用了5小时,求小明家到外婆家的距离.
例
3
知3-讲
感悟新知
解:设小明家到外婆家的距离是x千米,
由题意得:
解得:x=36
答:小明家到外婆家的距离是36千米.
知3-讲
感悟新知
总
结
根据找出等量关系是解答问题的关键.
知3-练
感悟新知
1.家住山脚下的孔明同学想从家出发去登山游玩,据以往的经验,他获得如下信息:
(1)他下山时的速度比上山时的速度每时快1千米;
(2)他上山2时到达的位置,离山顶还有1千米;
(3)抄近路下山,下山路程比上山路程近2千米;
(4)下山用1时.
知3-练
感悟新知
根据上面的信息,他作出如下计划:
(1)在山顶游览1时;
(2)中午12:00回到家吃午餐.
若依据以上信息和计划登山游玩,请问:孔明同学应该在什么时间从家出发?
知3-练
感悟新知
解:设上山的速度为v千米/时,
则下山的速度为(v+1)千米/时,
由题意得2v+1=v+1+2,解得v=2.
即上山的速度是2千米/时,下山的速度是3千米/时.
故上山用的时间为2+1÷2=2.5(时).
所以共用时间为2.5+1+1=4.5(时),
所以出发时间为12:00-4时30分=7:30.
故孔明同学应该在7:30从家出发.
课堂小结
用一元一次方程解行程问题
行程问题有相遇问题,追及问题,顺流、逆流问题,上坡、下坡问题等.在运动形式上分直线运动及曲线运动(如环形跑道).相遇问题是相向而行,相遇时的总路程为两运动物体的路程和.追及问题是同向而行,分慢的在快的前面或慢的先行若干时间,快的再追.顺流、逆流、顺风、逆风、上下坡等问题应注意运动方向.
必做:
请完成教材课后习题
课后作业
作业
同课章节目录
