2021-2022学年北师大版八年级数学上册1.2一定是直角三角形吗同步课时训练 (辽宁地区专用,Word版,附答案解析)
文档属性
| 名称 | 2021-2022学年北师大版八年级数学上册1.2一定是直角三角形吗同步课时训练 (辽宁地区专用,Word版,附答案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 221.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-29 15:29:54 | ||
图片预览




文档简介
同步课时训练-2021-2022学年八年级数学北师大版上册 (辽宁地区专用)
1.2一定是直接三角形吗
一、单选题(在下列各题的四个选项中,只有一项是符合题意的.本题共8个小题)
1.下列各组数中,可以构成直角三角形的一组是( ).
A.3,5,6 B.2,3,4 C.6,7,9 D.1.5,2,2.5
2.一个三角形的三边长为3,4,5,则此三角形最大边上的高为( )
A.2 B.2.4 C.4.8 D.9.6
3.在△ABC中,AB﹦12,BC﹦16,AC﹦20,则△ABC的面积是( )
A.120 B.160 C.216 D.96
4.如图,点A、B、C分别表示三个村庄,AB=13千米,BC=5千米,AC=12千米,某社区拟建一个文化活动中心.要求这三个村庄到活动中心的距离相等,则活动中心P的位置应在( )
A.AC中点 B.BC中点 C.AB中点 D.∠C的平分线与AB的交点
4题图 8题图
5.将直角三角形的三条边长同时扩大为原来的2倍,得到的三角形是 ( )
A.钝角三角形 B.锐角三角形 C.直角三角形 D.无法确定
6.适合下列条件的△ABC中,直角三角形的个数为( )
①afalse,bfalse,cfalse②a=6,∠A=45°;③∠A=32°,∠B=58°;④a=7,b=24,c=25⑤a=2,b=2,c=4.
A.2个 B.3个 C.4个 D.5个
7.如果△ABC的三边分别为m2-1,2 m,m2+1(m>1)那么( )
A.△ABC是直角三角形,且斜边长为m2+1
B.△ABC是直角三角形,且斜边长为2m
C.△ABC是直角三角形,但斜边长需由m的大小确定
D.△ABC不是直角三角形
8.如图:在一个边长为1的小正方形组成的方格稿纸上,有A、B、C、D、E、F、G七个点,则在下列任选三个点的方案中可以构成直角三角形的是( )
A.点A、点B、点C B.点A、点D、点G
C.点B、点E、点F D.点B、点G、点E
二、填空题
9.一个三角形的三边长分别为3,4,5,则这个三角形中最短边上的高为______.
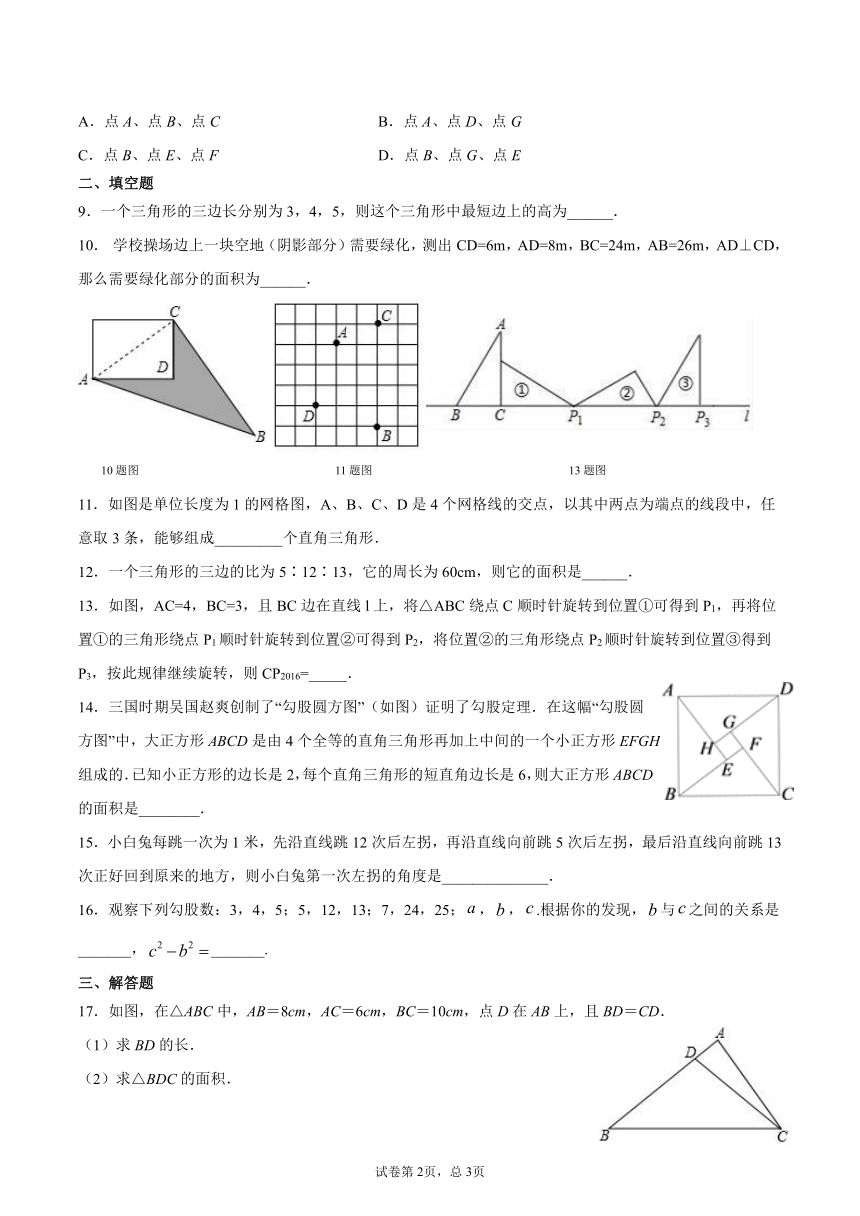
10. 学校操场边上一块空地(阴影部分)需要绿化,测出CD=6m,AD=8m,BC=24m,AB=26m,AD⊥CD,那么需要绿化部分的面积为______.
10题图 11题图 13题图
11.如图是单位长度为1的网格图,A、B、C、D是4个网格线的交点,以其中两点为端点的线段中,任意取3条,能够组成_________个直角三角形.
12.一个三角形的三边的比为5∶12∶13,它的周长为60cm,则它的面积是______.
513905582550013.如图,AC=4,BC=3,且BC边在直线l上,将△ABC绕点C顺时针旋转到位置①可得到P1,再将位置①的三角形绕点P1顺时针旋转到位置②可得到P2,将位置②的三角形绕点P2顺时针旋转到位置③得到P3,按此规律继续旋转,则CP2016=_____.
14.三国时期吴国赵爽创制了“勾股圆方图”(如图)证明了勾股定理.在这幅“勾股圆方图”中,大正方形ABCD是由4个全等的直角三角形再加上中间的一个小正方形EFGH组成的.已知小正方形的边长是2,每个直角三角形的短直角边长是6,则大正方形ABCD的面积是________.
15.小白兔每跳一次为1米,先沿直线跳12次后左拐,再沿直线向前跳5次后左拐,最后沿直线向前跳13次正好回到原来的地方,则小白兔第一次左拐的角度是______________.
16.观察下列勾股数:3,4,5;5,12,13;7,24,25;false,false,false.根据你的发现,false与false之间的关系是_______,false_______.
三、解答题
458724029210017.如图,在△ABC中,AB=8cm,AC=6cm,BC=10cm,点D在AB上,且BD=CD.
(1)求BD的长.
(2)求△BDC的面积.
4589145-27114518.如图,△ABC中,∠C=90°.
(1)在BC边上作一点P,使得点P到点C的距离与点P到边AB的距离相等(尺规作图,不写作法,保留作图痕迹);
(2)在(1)的条件下,若AC=4,BC=3,求CP的长.
5215255269240
19.如图,在△ABC中,AD=15,AC=12,DC=9,点B是CD延长线上一点,连接AB,若AB=20.
求:△ABD的面积.
已知a,b,c为△ABC三边,且满足a2+b2+c2+338=10a+24b+26c.试判断△ABC的形状.
21.某开发区有一空地ABCD,如图所示,现计划在空地上种草皮,经测量,
435229076835∠B=90?,AB =3m,BC=4m,AD=12m,CD=13m,若每种植1平方米草皮需要100元,问总共需要投入多少元?
22.观察下列勾股数:3,4,5;5,12,13;7,24,25;9,40,41;…;false,false,false.
根据你发现的规律,请求出:
(1)当false时,false,false的值;
(2)当false时,false,false的值.
参考答案
1.D
【思路点拨】知道三条边的大小,用较小的两条边的平方和与最大的边的平方比较,如果相等,则三角形为直角三角形;否则不是.
【详细解答】解:A. 32+52≠62,不能构成直角三角形,故选项错误;
B、22+32≠42,不能构成直角三角形,故选项错误;
C、62+72≠92,不能构成直角三角形,故选项错误;
D、1.52+22=2.52,能构成直角三角形,故选项正确.
故选:D
【方法总结】本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.
2.B
【思路点拨】根据勾股定理的逆定理可知该三角形为直角三角形,再根据三角形的面积公式,列出方程化简即可得出答案.
【详细解答】解:false
false三角形是直角三角形,长为5的边是最大边,长为3,4的边分别为直角边,
设斜边上的高为false,则根据直角三角形的面积公式知:false,
false
故选:B.
【方法总结】本题考察了利用了勾股定理的逆定理的应用,根据直角三角形的面积公式求出斜边上的高的长是解题的关键.
3.D
【详细解答】false 是直角三角形. false .故选D.
4.C
【思路点拨】先根据勾股定理的逆定理得出三角形是直角三角形,再根据直角三角形斜边上中线的性质得出即可.
【详细解答】解:∵AB=13千米,BC=5千米,AC=12千米,
∴BC2+AC2=AB2,
∴∠C=90°,
根据直角三角形斜边上的中线等于斜边的一半,得出活动中心P的位置应为斜边AB的中点,
故选:C.
【方法总结】本题考查了勾股定理的逆定理和直角三角形斜边上的中线性质等知识;熟练掌握勾股定理的逆定理是解此题的关键,注意:直角三角形斜边上的中线等于斜边的一半.
5.C
【思路点拨】根据勾股定理得出a2+b2=c2,推出4a2+4b2=4c2,得出(2a)2+(2b)2=(2c)2,根据勾股定理的逆定理得出即可.
【详细解答】解:∵设原直角三角形的三边的长是a、b、c,则a2+b2=c2,如图,
∴4a2+4b2=4c2,
即(2a)2+(2b)2=(2c)2,
∴将直角三角形的三条边长同时扩大2倍,得到的三角形还是直角三角形,
故选:C.
【方法总结】本题考查了勾股定理和勾股定理的逆定理的应用,掌握如果一个三角形的两边的平方和等于第三边的平方,那么这个三角形是直角三角形是关键.
6.A
【思路点拨】计算出三角形的角利用定义判定或在知道边的情况下利用勾股定理的逆定理判定则可.
【详细解答】①false,故△ABC不是直角三角形;
②a=6,∠A=45°不是成为直角三角形的必要条件,故△ABC不是直角三角形;
③∠A=32°,∠B=58°,∠C=180°-∠A-∠B=90°,故△ABC是直角三角形;
④72+242=252,故△ABC是直角三角形;
⑤22+22≠42,故△ABC不是直角三角形.
故选A.
【方法总结】本题考查了直角三角形的定义和勾股定理的逆定理,在应用勾股定理的逆定理时,应先认真分析所给边的大小关系,确定最大边后,再验证两条较小边的平方和与最大边的平方之间的关系,进而作出判断.
7.A
【思路点拨】根据勾股定理的逆定理即可判断.
【详细解答】解:∵(m2-1)2+(2 m)2=(m2+1)2,
∴三角形为直角三角形,且斜边长为m2+1,
故选A.
考点:本题考查的是勾股定理的逆定理
点评:解答本题的关键是熟记勾股定理的逆定理:如果三角形中两边的平方和等于第三边的平方,那么这个三角形一定是直角三角形.
8.C
【思路点拨】先利用勾股定理求出各边的长,再利用勾股定理的逆定理:如果三边满足false,则可组成直角三角形进行判断即可.
【详细解答】A.AB2=1+36=37,AC2=16+25=41,BC2=1+9=10,37+10≠41,不可以构成直角三角形;
B.AD2=16+16=32,AG2=9+36=45,DG2=1+4=5,32+5≠45,不可以构成直角三角形;
C.BE2=36+16=52,BF2=25+25=50,EF2=1+1=2,50+2=52,可以构成直角三角形
D.BG2=25+9=34,BE2=36+16=52,GE2=9+1=10,34+10≠52,不可以构成直角三角形.
故选:C.
【方法总结】本题主要考查勾股定理及其逆定理,掌握勾股定理及其逆定理是解题的关键.
9.4
【思路点拨】根据勾股定理的逆定理,可以判断题目中三角形的形状,然后即可得到这个三角形中最短边上的高的长度,本题得意解决.
【详细解答】解:false,
false三边长分别为3,4,5的三角形是直角三角形,
false这个三角形中最短边上的高为4,
故答案为:4.
【方法总结】本题考查勾股定理的逆定理,会用勾股定理的逆定理判断三角形的形状是解答本题的关键.
10.288
【思路点拨】由false,则false为直角三角形,即可求解.
【详细解答】解:∵false,
∴false,
∵false,
∴false为直角三角形,
∴false
false
false
false,
故答案是:288.
【方法总结】本题考查的是勾股定理的应用,本题的关键是确定false,然后利用面积公式即可求解.
11.2
【详细解答】试题分析:根据小正方形的边长可分别求,,,,,,根据勾股定理的逆定理,由知△ADB是直角三角形,由知△ABC是直角三角形.共2个.
考点:勾股定理的逆定理
12.false
【思路点拨】设这个三角形的三边长分别为false,再根据周长可求出x的值,从而可得三边长,然后利用勾股定理的逆定理可得这个三角形是直角三角形,最后利用直角三角形的面积公式即可得.
【详细解答】由题意,设这个三角形的三边长分别为false
则false
解得false
则这个三角形的三边长分别为false
又false
false这个三角形是直角三角形,且两直角边长分别为false
则它的面积是false
故答案为:false.
【方法总结】本题考查了勾股定理的逆定理的应用等知识点,依据勾股定理的逆定理判定出这个三角形为直角三角形是解题关键.
13.8064
【思路点拨】由题意可得AB=5,观察图形可得每3次旋转,△ABC沿水平方向平移12,则可求得CP的值.
【详细解答】∵AC=4,BC=3,
∴AB=false=5,
由题意可得CP3=4+5+3=12,
∴每3次旋转,△ABC沿水平方向平移12,
∴CP2016=12×false=8064.
故答案是:8064.
【方法总结】考查了旋转的性质,图形的变化,找到变化的规律是本题的关键.
14.100
【详细解答】因为大正方形ABCD中4个直角三角形全等,根据全等三角形的性质可得:BE=AH=DG=CF=3,又因为小正方形的边长是1,所以BF=AE=DH=CG=3+1=4,
根据勾股定理可得:AB=AD=CD=BC=false=5,所以大正方形ABCD的面积是25,
故答案为25.
15.false
【详细解答】由题意得:小白兔第一次跳12米,第二次跳5米,第三次跳13米;
∵false米,
而13 ?=169,刚好符合直角三角形中勾股定理的逆定理,且第一次和第二次跳的距离为直角边.
故小白兔第一次左拐的角度是90°.
16.false false
【解析】
【思路点拨】仔细观察可发现给出的勾股数中,斜边与较大的直角边的差是1,通过代入3,4,5;5,12,13;7,24,25计算可得false.
【详细解答】观察得给出的勾股数中,斜边与较大直角边的差是1,即c?b=1;通过代入3,4,5;5,12,13;7,24,25计算可得52-42=32,132-122=52,252-242=72,即可得到false.
【方法总结】本题考查勾股数、规律和勾股定理,解题的关键是掌握勾股定理.
17.(1)BD=falsecm;(2)false cm2.
【思路点拨】(1)由勾股定理逆定理判断出∠BAC=90°,设BD=CD=xcm,则AD=(8-x)cm,对Rt△ADC由勾股定理列方程,解出x,即可求出BD;
(2)根据三角形的面积公式即可求出结论.
【详细解答】解:(1)∵AB=8cm,AC=6cm,BC=10cm,
∴AB2+AC2=BC2,
∴∠BAC=90°,
设BD=CD=xcm,则AD=(8-x)cm.
在Rt△ADC中,由勾股定理得:AD2+AC2=CD2,
即(8-x)2+62=x2,
解得x=false,
即BD=falsecm.
(2)S△BDC=falseBD·AC=false×false×6=false cm2.
【方法总结】此题考查的是勾股定理及逆定理,本题关键在于设出未知数,借助勾股定理列方程求解.
18.(1)作图见解析;(2)CP的长为false.
【详细解答】试题分析:(1)作∠CAB的平分线,交BC于点P,过点P作PD⊥AB于D,则PC=PD;
(2)先利用HL证明Rt△ADP≌Rt△ACP,得出AD=AC=3,再设PC=x,则PD=x,BP=4-x,在Rt△BDP中,由勾股定理得出(4-x)2=x2+12,解出x的值即可.
试题解析:(1)如图,点P即为所求;
(2)∵AP平分∠CAB,PD⊥AB于D,∠C=90°,∴PD=PC.
在Rt△ADP和Rt△ACP中,
false
∴Rt△ADP≌Rt△ACP(HL).
∴AD=AC=4.
在Rt△ABC中,由勾股定理,得AB=5.
∴BD=5﹣4=1.
设PC=x,则PD=x,BP=3﹣x,
在Rt△BDP中,由勾股定理,得PD2+BD2=PB2,
即(3﹣x)2=x2+12,
解得:x=false.
答:CP的长为false.
考点:1.角平分线的性质;2.勾股定理;3.作图—基本作图.
19.42.
【详细解答】试题分析:由勾股定理的逆定理证明△ADC是直角三角形,∠C=90°,再由勾股定理求出BC,得出BD,即可得出结果.
解:在△ADC中,AD=15,AC=12,DC=9,
AC2+DC2=122+92=152=AD2,
即AC2+DC2=AD2,
∴△ADC是直角三角形,∠C=90°,
在Rt△ABC中,BC===16,
∴BD=BC﹣DC=16﹣9=7,
∴△ABD的面积=×7×12=42.
20.直角三角形
【详细解答】试题分析:把已知条件写成三个完全平方式的和的形式,再由非负数的性质求得三边,根据勾股定理的逆定理即可判断△ABC的形状.
由已知得(a2-10a+25)+(b2-24b+144)+(c2-26c+169)=0
(a-5)2+(b-12)2+(c-13)2=0
由于(a-5)2≥0,(b-12)2≥0,(c-13)2≥0.
所以a-5=0,得a=5;
b-12=0,得b=12;
c-13=0,得c=13.
又因为132=52+122,即a2+b2=c2
所以△ABC是直角三角形.
考点:本题考查的是勾股定理的逆定理,非负数的性质
点评:解答本题的关键是熟记勾股定理的逆定理:如果三角形中两边的平方和等于第三边的平方,那么这个三角形一定是直角三角形.
21.3600(元)
【思路点拨】连接AC,在Rt△ABC中利用勾股定理求出AC,然后证明三角形ACD是直角三角形,即可求出面积,再进行计算.
【详细解答】连接AC,
在Rt△ABC中AC=false
在三角形ACD中,false
∴三角形ACD是直角三角形,
∴S四边形ABCD=false=36,
∴造价为36×100=3600(元)
22.(1)false,false;(2)false,false.
【思路点拨】题目明确告诉我们:“观察下列勾股数”,就是说这些数据一定都是勾股数,即满足a2+b2=c2;
再进一步观察猜想其规律,可以发现第二个数总是比第三个数小1,从而可以利用第二个数将第三个数表示出来,即c=b+1;由a的值和规律c=b+1,利用a2+b2=c2,即可列出关于b的方程,由方程的解可得到第(1)、(2)两小题中b、c的值.
【详细解答】(1)通过观察可知,false,
所以false,解得false,
因此false.
(2)根据题意,得false,
即false,解得false,false.
【方法总结】本题考查勾股定理,解题的关键是读懂题意,掌握勾股定理.
1.2一定是直接三角形吗
一、单选题(在下列各题的四个选项中,只有一项是符合题意的.本题共8个小题)
1.下列各组数中,可以构成直角三角形的一组是( ).
A.3,5,6 B.2,3,4 C.6,7,9 D.1.5,2,2.5
2.一个三角形的三边长为3,4,5,则此三角形最大边上的高为( )
A.2 B.2.4 C.4.8 D.9.6
3.在△ABC中,AB﹦12,BC﹦16,AC﹦20,则△ABC的面积是( )
A.120 B.160 C.216 D.96
4.如图,点A、B、C分别表示三个村庄,AB=13千米,BC=5千米,AC=12千米,某社区拟建一个文化活动中心.要求这三个村庄到活动中心的距离相等,则活动中心P的位置应在( )
A.AC中点 B.BC中点 C.AB中点 D.∠C的平分线与AB的交点
4题图 8题图
5.将直角三角形的三条边长同时扩大为原来的2倍,得到的三角形是 ( )
A.钝角三角形 B.锐角三角形 C.直角三角形 D.无法确定
6.适合下列条件的△ABC中,直角三角形的个数为( )
①afalse,bfalse,cfalse②a=6,∠A=45°;③∠A=32°,∠B=58°;④a=7,b=24,c=25⑤a=2,b=2,c=4.
A.2个 B.3个 C.4个 D.5个
7.如果△ABC的三边分别为m2-1,2 m,m2+1(m>1)那么( )
A.△ABC是直角三角形,且斜边长为m2+1
B.△ABC是直角三角形,且斜边长为2m
C.△ABC是直角三角形,但斜边长需由m的大小确定
D.△ABC不是直角三角形
8.如图:在一个边长为1的小正方形组成的方格稿纸上,有A、B、C、D、E、F、G七个点,则在下列任选三个点的方案中可以构成直角三角形的是( )
A.点A、点B、点C B.点A、点D、点G
C.点B、点E、点F D.点B、点G、点E
二、填空题
9.一个三角形的三边长分别为3,4,5,则这个三角形中最短边上的高为______.
10. 学校操场边上一块空地(阴影部分)需要绿化,测出CD=6m,AD=8m,BC=24m,AB=26m,AD⊥CD,那么需要绿化部分的面积为______.
10题图 11题图 13题图
11.如图是单位长度为1的网格图,A、B、C、D是4个网格线的交点,以其中两点为端点的线段中,任意取3条,能够组成_________个直角三角形.
12.一个三角形的三边的比为5∶12∶13,它的周长为60cm,则它的面积是______.
513905582550013.如图,AC=4,BC=3,且BC边在直线l上,将△ABC绕点C顺时针旋转到位置①可得到P1,再将位置①的三角形绕点P1顺时针旋转到位置②可得到P2,将位置②的三角形绕点P2顺时针旋转到位置③得到P3,按此规律继续旋转,则CP2016=_____.
14.三国时期吴国赵爽创制了“勾股圆方图”(如图)证明了勾股定理.在这幅“勾股圆方图”中,大正方形ABCD是由4个全等的直角三角形再加上中间的一个小正方形EFGH组成的.已知小正方形的边长是2,每个直角三角形的短直角边长是6,则大正方形ABCD的面积是________.
15.小白兔每跳一次为1米,先沿直线跳12次后左拐,再沿直线向前跳5次后左拐,最后沿直线向前跳13次正好回到原来的地方,则小白兔第一次左拐的角度是______________.
16.观察下列勾股数:3,4,5;5,12,13;7,24,25;false,false,false.根据你的发现,false与false之间的关系是_______,false_______.
三、解答题
458724029210017.如图,在△ABC中,AB=8cm,AC=6cm,BC=10cm,点D在AB上,且BD=CD.
(1)求BD的长.
(2)求△BDC的面积.
4589145-27114518.如图,△ABC中,∠C=90°.
(1)在BC边上作一点P,使得点P到点C的距离与点P到边AB的距离相等(尺规作图,不写作法,保留作图痕迹);
(2)在(1)的条件下,若AC=4,BC=3,求CP的长.
5215255269240
19.如图,在△ABC中,AD=15,AC=12,DC=9,点B是CD延长线上一点,连接AB,若AB=20.
求:△ABD的面积.
已知a,b,c为△ABC三边,且满足a2+b2+c2+338=10a+24b+26c.试判断△ABC的形状.
21.某开发区有一空地ABCD,如图所示,现计划在空地上种草皮,经测量,
435229076835∠B=90?,AB =3m,BC=4m,AD=12m,CD=13m,若每种植1平方米草皮需要100元,问总共需要投入多少元?
22.观察下列勾股数:3,4,5;5,12,13;7,24,25;9,40,41;…;false,false,false.
根据你发现的规律,请求出:
(1)当false时,false,false的值;
(2)当false时,false,false的值.
参考答案
1.D
【思路点拨】知道三条边的大小,用较小的两条边的平方和与最大的边的平方比较,如果相等,则三角形为直角三角形;否则不是.
【详细解答】解:A. 32+52≠62,不能构成直角三角形,故选项错误;
B、22+32≠42,不能构成直角三角形,故选项错误;
C、62+72≠92,不能构成直角三角形,故选项错误;
D、1.52+22=2.52,能构成直角三角形,故选项正确.
故选:D
【方法总结】本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.
2.B
【思路点拨】根据勾股定理的逆定理可知该三角形为直角三角形,再根据三角形的面积公式,列出方程化简即可得出答案.
【详细解答】解:false
false三角形是直角三角形,长为5的边是最大边,长为3,4的边分别为直角边,
设斜边上的高为false,则根据直角三角形的面积公式知:false,
false
故选:B.
【方法总结】本题考察了利用了勾股定理的逆定理的应用,根据直角三角形的面积公式求出斜边上的高的长是解题的关键.
3.D
【详细解答】false 是直角三角形. false .故选D.
4.C
【思路点拨】先根据勾股定理的逆定理得出三角形是直角三角形,再根据直角三角形斜边上中线的性质得出即可.
【详细解答】解:∵AB=13千米,BC=5千米,AC=12千米,
∴BC2+AC2=AB2,
∴∠C=90°,
根据直角三角形斜边上的中线等于斜边的一半,得出活动中心P的位置应为斜边AB的中点,
故选:C.
【方法总结】本题考查了勾股定理的逆定理和直角三角形斜边上的中线性质等知识;熟练掌握勾股定理的逆定理是解此题的关键,注意:直角三角形斜边上的中线等于斜边的一半.
5.C
【思路点拨】根据勾股定理得出a2+b2=c2,推出4a2+4b2=4c2,得出(2a)2+(2b)2=(2c)2,根据勾股定理的逆定理得出即可.
【详细解答】解:∵设原直角三角形的三边的长是a、b、c,则a2+b2=c2,如图,
∴4a2+4b2=4c2,
即(2a)2+(2b)2=(2c)2,
∴将直角三角形的三条边长同时扩大2倍,得到的三角形还是直角三角形,
故选:C.
【方法总结】本题考查了勾股定理和勾股定理的逆定理的应用,掌握如果一个三角形的两边的平方和等于第三边的平方,那么这个三角形是直角三角形是关键.
6.A
【思路点拨】计算出三角形的角利用定义判定或在知道边的情况下利用勾股定理的逆定理判定则可.
【详细解答】①false,故△ABC不是直角三角形;
②a=6,∠A=45°不是成为直角三角形的必要条件,故△ABC不是直角三角形;
③∠A=32°,∠B=58°,∠C=180°-∠A-∠B=90°,故△ABC是直角三角形;
④72+242=252,故△ABC是直角三角形;
⑤22+22≠42,故△ABC不是直角三角形.
故选A.
【方法总结】本题考查了直角三角形的定义和勾股定理的逆定理,在应用勾股定理的逆定理时,应先认真分析所给边的大小关系,确定最大边后,再验证两条较小边的平方和与最大边的平方之间的关系,进而作出判断.
7.A
【思路点拨】根据勾股定理的逆定理即可判断.
【详细解答】解:∵(m2-1)2+(2 m)2=(m2+1)2,
∴三角形为直角三角形,且斜边长为m2+1,
故选A.
考点:本题考查的是勾股定理的逆定理
点评:解答本题的关键是熟记勾股定理的逆定理:如果三角形中两边的平方和等于第三边的平方,那么这个三角形一定是直角三角形.
8.C
【思路点拨】先利用勾股定理求出各边的长,再利用勾股定理的逆定理:如果三边满足false,则可组成直角三角形进行判断即可.
【详细解答】A.AB2=1+36=37,AC2=16+25=41,BC2=1+9=10,37+10≠41,不可以构成直角三角形;
B.AD2=16+16=32,AG2=9+36=45,DG2=1+4=5,32+5≠45,不可以构成直角三角形;
C.BE2=36+16=52,BF2=25+25=50,EF2=1+1=2,50+2=52,可以构成直角三角形
D.BG2=25+9=34,BE2=36+16=52,GE2=9+1=10,34+10≠52,不可以构成直角三角形.
故选:C.
【方法总结】本题主要考查勾股定理及其逆定理,掌握勾股定理及其逆定理是解题的关键.
9.4
【思路点拨】根据勾股定理的逆定理,可以判断题目中三角形的形状,然后即可得到这个三角形中最短边上的高的长度,本题得意解决.
【详细解答】解:false,
false三边长分别为3,4,5的三角形是直角三角形,
false这个三角形中最短边上的高为4,
故答案为:4.
【方法总结】本题考查勾股定理的逆定理,会用勾股定理的逆定理判断三角形的形状是解答本题的关键.
10.288
【思路点拨】由false,则false为直角三角形,即可求解.
【详细解答】解:∵false,
∴false,
∵false,
∴false为直角三角形,
∴false
false
false
false,
故答案是:288.
【方法总结】本题考查的是勾股定理的应用,本题的关键是确定false,然后利用面积公式即可求解.
11.2
【详细解答】试题分析:根据小正方形的边长可分别求,,,,,,根据勾股定理的逆定理,由知△ADB是直角三角形,由知△ABC是直角三角形.共2个.
考点:勾股定理的逆定理
12.false
【思路点拨】设这个三角形的三边长分别为false,再根据周长可求出x的值,从而可得三边长,然后利用勾股定理的逆定理可得这个三角形是直角三角形,最后利用直角三角形的面积公式即可得.
【详细解答】由题意,设这个三角形的三边长分别为false
则false
解得false
则这个三角形的三边长分别为false
又false
false这个三角形是直角三角形,且两直角边长分别为false
则它的面积是false
故答案为:false.
【方法总结】本题考查了勾股定理的逆定理的应用等知识点,依据勾股定理的逆定理判定出这个三角形为直角三角形是解题关键.
13.8064
【思路点拨】由题意可得AB=5,观察图形可得每3次旋转,△ABC沿水平方向平移12,则可求得CP的值.
【详细解答】∵AC=4,BC=3,
∴AB=false=5,
由题意可得CP3=4+5+3=12,
∴每3次旋转,△ABC沿水平方向平移12,
∴CP2016=12×false=8064.
故答案是:8064.
【方法总结】考查了旋转的性质,图形的变化,找到变化的规律是本题的关键.
14.100
【详细解答】因为大正方形ABCD中4个直角三角形全等,根据全等三角形的性质可得:BE=AH=DG=CF=3,又因为小正方形的边长是1,所以BF=AE=DH=CG=3+1=4,
根据勾股定理可得:AB=AD=CD=BC=false=5,所以大正方形ABCD的面积是25,
故答案为25.
15.false
【详细解答】由题意得:小白兔第一次跳12米,第二次跳5米,第三次跳13米;
∵false米,
而13 ?=169,刚好符合直角三角形中勾股定理的逆定理,且第一次和第二次跳的距离为直角边.
故小白兔第一次左拐的角度是90°.
16.false false
【解析】
【思路点拨】仔细观察可发现给出的勾股数中,斜边与较大的直角边的差是1,通过代入3,4,5;5,12,13;7,24,25计算可得false.
【详细解答】观察得给出的勾股数中,斜边与较大直角边的差是1,即c?b=1;通过代入3,4,5;5,12,13;7,24,25计算可得52-42=32,132-122=52,252-242=72,即可得到false.
【方法总结】本题考查勾股数、规律和勾股定理,解题的关键是掌握勾股定理.
17.(1)BD=falsecm;(2)false cm2.
【思路点拨】(1)由勾股定理逆定理判断出∠BAC=90°,设BD=CD=xcm,则AD=(8-x)cm,对Rt△ADC由勾股定理列方程,解出x,即可求出BD;
(2)根据三角形的面积公式即可求出结论.
【详细解答】解:(1)∵AB=8cm,AC=6cm,BC=10cm,
∴AB2+AC2=BC2,
∴∠BAC=90°,
设BD=CD=xcm,则AD=(8-x)cm.
在Rt△ADC中,由勾股定理得:AD2+AC2=CD2,
即(8-x)2+62=x2,
解得x=false,
即BD=falsecm.
(2)S△BDC=falseBD·AC=false×false×6=false cm2.
【方法总结】此题考查的是勾股定理及逆定理,本题关键在于设出未知数,借助勾股定理列方程求解.
18.(1)作图见解析;(2)CP的长为false.
【详细解答】试题分析:(1)作∠CAB的平分线,交BC于点P,过点P作PD⊥AB于D,则PC=PD;
(2)先利用HL证明Rt△ADP≌Rt△ACP,得出AD=AC=3,再设PC=x,则PD=x,BP=4-x,在Rt△BDP中,由勾股定理得出(4-x)2=x2+12,解出x的值即可.
试题解析:(1)如图,点P即为所求;
(2)∵AP平分∠CAB,PD⊥AB于D,∠C=90°,∴PD=PC.
在Rt△ADP和Rt△ACP中,
false
∴Rt△ADP≌Rt△ACP(HL).
∴AD=AC=4.
在Rt△ABC中,由勾股定理,得AB=5.
∴BD=5﹣4=1.
设PC=x,则PD=x,BP=3﹣x,
在Rt△BDP中,由勾股定理,得PD2+BD2=PB2,
即(3﹣x)2=x2+12,
解得:x=false.
答:CP的长为false.
考点:1.角平分线的性质;2.勾股定理;3.作图—基本作图.
19.42.
【详细解答】试题分析:由勾股定理的逆定理证明△ADC是直角三角形,∠C=90°,再由勾股定理求出BC,得出BD,即可得出结果.
解:在△ADC中,AD=15,AC=12,DC=9,
AC2+DC2=122+92=152=AD2,
即AC2+DC2=AD2,
∴△ADC是直角三角形,∠C=90°,
在Rt△ABC中,BC===16,
∴BD=BC﹣DC=16﹣9=7,
∴△ABD的面积=×7×12=42.
20.直角三角形
【详细解答】试题分析:把已知条件写成三个完全平方式的和的形式,再由非负数的性质求得三边,根据勾股定理的逆定理即可判断△ABC的形状.
由已知得(a2-10a+25)+(b2-24b+144)+(c2-26c+169)=0
(a-5)2+(b-12)2+(c-13)2=0
由于(a-5)2≥0,(b-12)2≥0,(c-13)2≥0.
所以a-5=0,得a=5;
b-12=0,得b=12;
c-13=0,得c=13.
又因为132=52+122,即a2+b2=c2
所以△ABC是直角三角形.
考点:本题考查的是勾股定理的逆定理,非负数的性质
点评:解答本题的关键是熟记勾股定理的逆定理:如果三角形中两边的平方和等于第三边的平方,那么这个三角形一定是直角三角形.
21.3600(元)
【思路点拨】连接AC,在Rt△ABC中利用勾股定理求出AC,然后证明三角形ACD是直角三角形,即可求出面积,再进行计算.
【详细解答】连接AC,
在Rt△ABC中AC=false
在三角形ACD中,false
∴三角形ACD是直角三角形,
∴S四边形ABCD=false=36,
∴造价为36×100=3600(元)
22.(1)false,false;(2)false,false.
【思路点拨】题目明确告诉我们:“观察下列勾股数”,就是说这些数据一定都是勾股数,即满足a2+b2=c2;
再进一步观察猜想其规律,可以发现第二个数总是比第三个数小1,从而可以利用第二个数将第三个数表示出来,即c=b+1;由a的值和规律c=b+1,利用a2+b2=c2,即可列出关于b的方程,由方程的解可得到第(1)、(2)两小题中b、c的值.
【详细解答】(1)通过观察可知,false,
所以false,解得false,
因此false.
(2)根据题意,得false,
即false,解得false,false.
【方法总结】本题考查勾股定理,解题的关键是读懂题意,掌握勾股定理.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
