2021-2022学年苏科版八年级上册数学 1.2全等三角形 同步练(预习)(word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版八年级上册数学 1.2全等三角形 同步练(预习)(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 103.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-30 00:00:00 | ||
图片预览

文档简介
全等三角形
知识点1:全等三角形
全等三角形的概念:能够___________的图形叫全等三角形
表示方法:如果△ABC和△DEF是全等三角形,可记作△ABC≌△DEF,读作△ABC全等于△DEF
对应元素:把两个全等的三角形重合在一起
对应顶点:_______的顶点
对应边:_______的边
对应角:_______的角
找对应边:
两个全等三角形的最长边是对应边,最短边是对应边
两个全等三角形的公共边是对应边
两个全等三角形的对应角,所对的边是对应边;两个对角所夹的边是对应边
已知两个全等三角形的两组对应边,则第三组边必为对应边
找对应角:
两个全等三角形的_______角是对应角,________角是对应角。
两个全等三角形的公共角是对应角。一组_______角是对应角。
两个全等三角形对应边所对的角是对应角,两组对应边所夹的角是对应角。
已知两个全等三角形的两组对应角,则第三组角___________。
知识点2:全等三角形的性质
全等三角形的对应边_____,对应角_____
全等三角形的周长_____,面积_____
知识点3:三角形的全等变换
全等变化的概念:只改变图形的位置,而不改变其形状大小的图形变换,叫做全等变换
三种常见的全等变换:平移全等形、翻折全等形、旋转全等形
一、选择题
1. 如图,△AOC≌△BOD,点A与点B是对应点,那么下列结论中错误的是( )
A.AB=CD B.AC=BD C.AO=BO D.∠A=∠B
2.如图,△ABC≌△DEC,B、C、D在同一直线上,且CE=5,AC=7,则BD长( )
A.12 B.7 C.2 D.14
3. 如图,若△ABC≌△DEF,B、E、C、F在同一直线上,BC=7,EC=4,则CF的长是( )
A.2 B.3 C.5 D.7
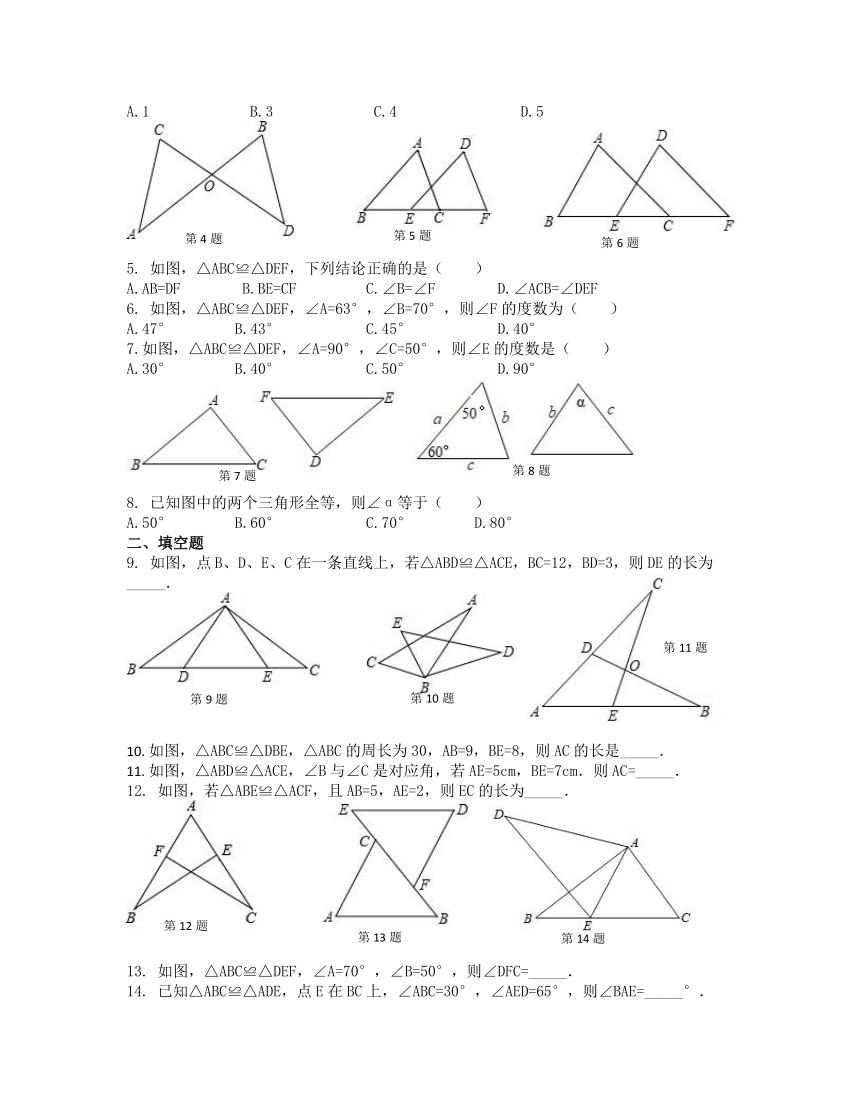
4. 如图,△OCA≌△OBD,AO=3,CO=2,则AB的长为( )
A.1 B.3 C.4 D.5
5. 如图,△ABC≌△DEF,下列结论正确的是( )
A.AB=DF B.BE=CF C.∠B=∠F D.∠ACB=∠DEF
6. 如图,△ABC≌△DEF,∠A=63°,∠B=70°,则∠F的度数为( )
A.47° B.43° C.45° D.40°
7.如图,△ABC≌△DEF,∠A=90°,∠C=50°,则∠E的度数是( )
A.30° B.40° C.50° D.90°
8. 已知图中的两个三角形全等,则∠α等于( )
A.50° B.60° C.70° D.80°
二、填空题
9. 如图,点 B、D、E、C在一条直线上,若△ABD≌△ACE,BC=12,BD=3,则DE的长为_____.
如图,△ABC≌△DBE,△ABC的周长为30,AB=9,BE=8,则AC的长是_____.
如图,△ABD≌△ACE,∠B与∠C是对应角,若AE=5cm,BE=7cm.则AC=_____.
如图,若△ABE≌△ACF,且AB=5,AE=2,则EC的长为_____.
13. 如图,△ABC≌△DEF,∠A=70°,∠B=50°,则∠DFC=_____.
14. 已知△ABC≌△ADE,点E在BC上,∠ABC=30°,∠AED=65°,则∠BAE=_____°.
15. 如图,△ACB≌△A'CB',若∠ACB=60°,∠ACB'=100°,则∠BCA'=_____°.
16. 如图,△ABC≌△DCB,AB和DC是对应边,∠DBC=40°,则∠AOD=_____度.
解答题
17.如图,已知△ABC≌△DEB,点E在AB上,AC与BD交于点F,AB=6,BC=3,∠C=55°,∠D=25°.
(1)求AE的长度;
(2)求∠AED的度数.
18.已知,如图,△ABC≌△DEF,求证:AC∥DF.
19. 如图,△AEC≌△ADB,若∠A=60°,∠ACE=35°,且∠1=∠2,求∠1的度数.
A
A
B
D
B
A
B
C
6
13
12cm
3
60°
35
20
100
(1)∵△ABC≌△DEB,
∴BE=BC=3,
∴AE=AB-BE=6-3=3;
(2)∵△ABC≌△DEB,
∴∠A=∠D=25°,∠DBE=∠C=55°,
∴∠AED=∠DBE+∠D=25°+55°=80°
18、证明:∵△ABC≌△DEF,
∴∠ACB=∠DFE,
∴AC∥DF
19、解:∵△AEC≌△ADB,
∴AC=AB,
∴∠ABC=∠ACB,
∵∠A=60°,
∴∠ABC=∠ACB=60°,
∵∠ACE=35°,∠1=∠2,
∴∠1=∠2=∠ACB-∠ACE=60°-35°=25°
知识点1:全等三角形
全等三角形的概念:能够___________的图形叫全等三角形
表示方法:如果△ABC和△DEF是全等三角形,可记作△ABC≌△DEF,读作△ABC全等于△DEF
对应元素:把两个全等的三角形重合在一起
对应顶点:_______的顶点
对应边:_______的边
对应角:_______的角
找对应边:
两个全等三角形的最长边是对应边,最短边是对应边
两个全等三角形的公共边是对应边
两个全等三角形的对应角,所对的边是对应边;两个对角所夹的边是对应边
已知两个全等三角形的两组对应边,则第三组边必为对应边
找对应角:
两个全等三角形的_______角是对应角,________角是对应角。
两个全等三角形的公共角是对应角。一组_______角是对应角。
两个全等三角形对应边所对的角是对应角,两组对应边所夹的角是对应角。
已知两个全等三角形的两组对应角,则第三组角___________。
知识点2:全等三角形的性质
全等三角形的对应边_____,对应角_____
全等三角形的周长_____,面积_____
知识点3:三角形的全等变换
全等变化的概念:只改变图形的位置,而不改变其形状大小的图形变换,叫做全等变换
三种常见的全等变换:平移全等形、翻折全等形、旋转全等形
一、选择题
1. 如图,△AOC≌△BOD,点A与点B是对应点,那么下列结论中错误的是( )
A.AB=CD B.AC=BD C.AO=BO D.∠A=∠B
2.如图,△ABC≌△DEC,B、C、D在同一直线上,且CE=5,AC=7,则BD长( )
A.12 B.7 C.2 D.14
3. 如图,若△ABC≌△DEF,B、E、C、F在同一直线上,BC=7,EC=4,则CF的长是( )
A.2 B.3 C.5 D.7
4. 如图,△OCA≌△OBD,AO=3,CO=2,则AB的长为( )
A.1 B.3 C.4 D.5
5. 如图,△ABC≌△DEF,下列结论正确的是( )
A.AB=DF B.BE=CF C.∠B=∠F D.∠ACB=∠DEF
6. 如图,△ABC≌△DEF,∠A=63°,∠B=70°,则∠F的度数为( )
A.47° B.43° C.45° D.40°
7.如图,△ABC≌△DEF,∠A=90°,∠C=50°,则∠E的度数是( )
A.30° B.40° C.50° D.90°
8. 已知图中的两个三角形全等,则∠α等于( )
A.50° B.60° C.70° D.80°
二、填空题
9. 如图,点 B、D、E、C在一条直线上,若△ABD≌△ACE,BC=12,BD=3,则DE的长为_____.
如图,△ABC≌△DBE,△ABC的周长为30,AB=9,BE=8,则AC的长是_____.
如图,△ABD≌△ACE,∠B与∠C是对应角,若AE=5cm,BE=7cm.则AC=_____.
如图,若△ABE≌△ACF,且AB=5,AE=2,则EC的长为_____.
13. 如图,△ABC≌△DEF,∠A=70°,∠B=50°,则∠DFC=_____.
14. 已知△ABC≌△ADE,点E在BC上,∠ABC=30°,∠AED=65°,则∠BAE=_____°.
15. 如图,△ACB≌△A'CB',若∠ACB=60°,∠ACB'=100°,则∠BCA'=_____°.
16. 如图,△ABC≌△DCB,AB和DC是对应边,∠DBC=40°,则∠AOD=_____度.
解答题
17.如图,已知△ABC≌△DEB,点E在AB上,AC与BD交于点F,AB=6,BC=3,∠C=55°,∠D=25°.
(1)求AE的长度;
(2)求∠AED的度数.
18.已知,如图,△ABC≌△DEF,求证:AC∥DF.
19. 如图,△AEC≌△ADB,若∠A=60°,∠ACE=35°,且∠1=∠2,求∠1的度数.
A
A
B
D
B
A
B
C
6
13
12cm
3
60°
35
20
100
(1)∵△ABC≌△DEB,
∴BE=BC=3,
∴AE=AB-BE=6-3=3;
(2)∵△ABC≌△DEB,
∴∠A=∠D=25°,∠DBE=∠C=55°,
∴∠AED=∠DBE+∠D=25°+55°=80°
18、证明:∵△ABC≌△DEF,
∴∠ACB=∠DFE,
∴AC∥DF
19、解:∵△AEC≌△ADB,
∴AC=AB,
∴∠ABC=∠ACB,
∵∠A=60°,
∴∠ABC=∠ACB=60°,
∵∠ACE=35°,∠1=∠2,
∴∠1=∠2=∠ACB-∠ACE=60°-35°=25°
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
