2.2轴对称的性质 一课一练 2021-2022学年苏科版八年级 上册 数学(Word版 含答案)
文档属性
| 名称 | 2.2轴对称的性质 一课一练 2021-2022学年苏科版八年级 上册 数学(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 430.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-30 10:55:05 | ||
图片预览



文档简介
(苏科版)2021-2022学年八年级(上册)数学一课一练
2.2轴对称的性质
一、单选题
1.分别以直线false为对称轴,所作轴对称图形错误的是( )
A.B.C.D.
2.已知点A(2,false)关于x轴对称的点的坐标为点B(false,false),则false的值为( )
A.-5 B.-1 C.1 D.5
3.横撇竖捺,构架成一个个文字,在下列表示生肖的方块字中,是轴对称图形的是( )
A. B. C. D.
4.如图,直线false是多边形false的对称轴,false,false,那么false( )
A.false B.false C.false D.false
5.如图,△ABC与△A′B′C′关于直线MN对称,P为MN上任一点(A、P、A′不共线),下列结论中错误的是( )
A.△AA′P是等腰三角形 B.MN垂直平分AA′、CC′
C.△ABC与△A′B′C′面积相等 D.直线AB,A′B′的交点不一定在直线MN上
6.如图所示,哪一个选项中的左边图形与右边图形成轴对称( )
A. B. C. D.
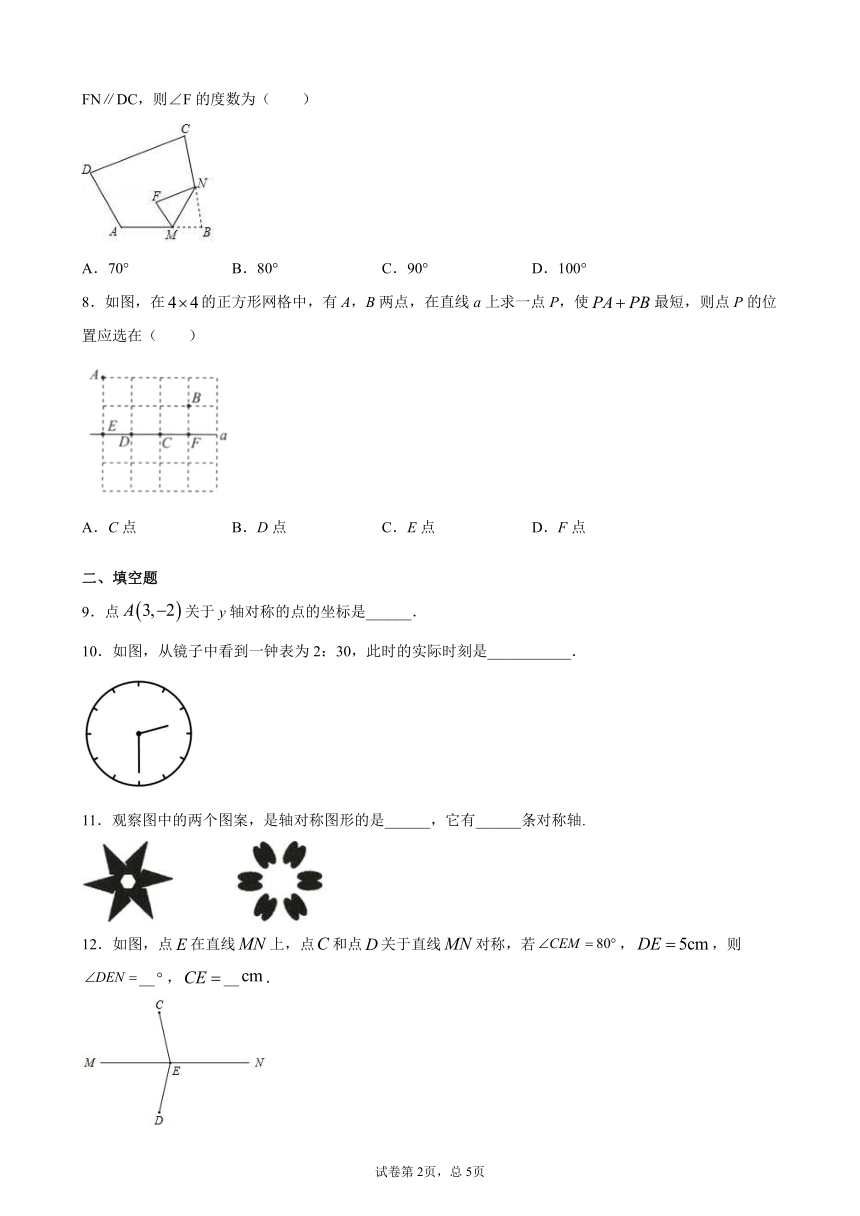
7.如图,在四边形ABCD中,∠A=120°,∠C=80°.将△BMN沿着MN翻折,得到△FMN.若MF∥AD,FN∥DC,则∠F的度数为( )
A.70° B.80° C.90° D.100°
8.如图,在false的正方形网格中,有A,B两点,在直线a上求一点P,使false最短,则点P的位置应选在( )
A.C点 B.D点 C.E点 D.F点
二、填空题
9.点false关于y轴对称的点的坐标是______.
10.如图,从镜子中看到一钟表为2:30,此时的实际时刻是___________.
11.观察图中的两个图案,是轴对称图形的是______,它有______条对称轴.
12.如图,点false在直线false上,点false和点false关于直线false对称,若false,false,则false__false,false__false.
13.如图,直线false是三角形false的对称轴,点false,false是线段false上的两点.若false,false,则图中阴影部分的面积是________.
14.如图所示的false组图形中,左、右两个图形成轴对称的是第_________________组.
15.一个汽车牌在水中的倒影为,则该车牌照号码___________.
16.下图是小明在平面镜里看到的电子钟示数,这时的实际时间是________.
三、解答题
17.如图所示的五角星共有几条对称轴?请你在下图中分别画出来.
18.如图所示的是在一面镜子里看到的一个算式,该算式的实际情况是怎样的?
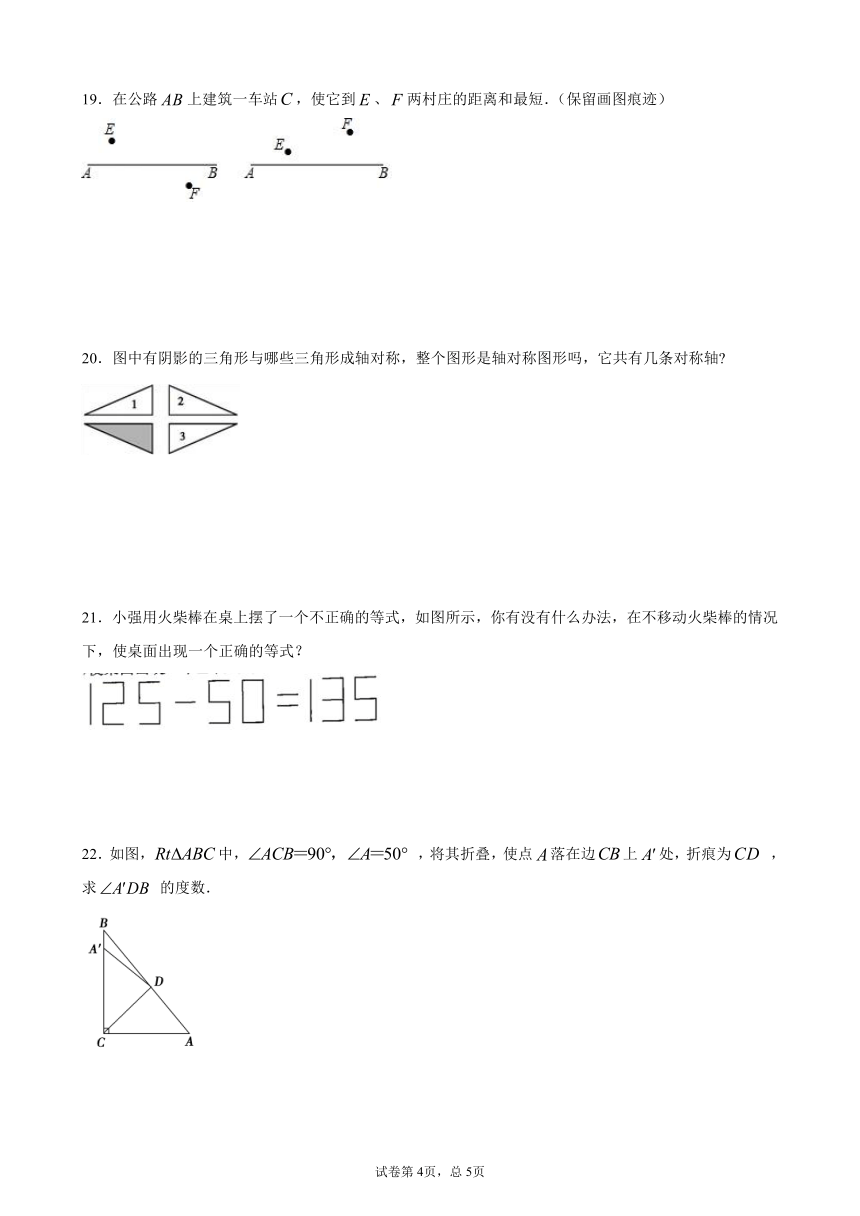
19.在公路false上建筑一车站false,使它到false、false两村庄的距离和最短.(保留画图痕迹)
20.图中有阴影的三角形与哪些三角形成轴对称,整个图形是轴对称图形吗,它共有几条对称轴?
21.小强用火柴棒在桌上摆了一个不正确的等式,如图所示,你有没有什么办法,在不移动火柴棒的情况下,使桌面出现一个正确的等式?
22.如图,false中,false ,将其折叠,使点false落在边false上false处,折痕为false ,求false 的度数.
23.如图,false、false分别是false的边false、false上的点,在false上求作一点false,使false的周长最小,并说明你这样作的理由.
24.只利用一把有刻度的直尺,用度量的方法按下列要求画图:
(1)在图①中用下面的方法画等腰三角形ABC的对称轴.
①量出底边BC的长度,将线段BC二等分,即画出BC的中点D;
②画直线AD,即画出等腰三角形ABC的对称轴.
(2)在图②中画∠AOB的对称轴,并写出画图的方法.
参考答案
1.C
【解析】根据轴对称的定义可知C中图形沿直线false对折后直线false两旁的部分不能重合,
故选C.
2.B
【解析】因为点A关于x轴对称所以false=2,false=3可解得m=1,n=2, false=1-2=-1
故选:B
3.D
【解析】解:根据轴对称图形的定义知:
为轴对称图形,其它选项不符合题意.
故选:D.
4.C
【解析】解:根据题意:直线m是多边形ABCDEFGH的对称轴,BC∥AD∥m,∠B=130°,
那么∠GHA=(6×180°-4×130°)÷4=140°.
故选:C.
5.D
【解析】解:∵△ABC与△A′B′C′关于直线MN对称,P为MN上任意一点,
∴△AA′P是等腰三角形,MN垂直平分AA′,CC′,这两个三角形的面积相等,故A、B、C选项正确,
直线AB,A′B′关于直线MN对称,因此交点一定在MN上,故D错误,
故选:D.
6.C
【解析】根据轴对称图形的定义即判断方法可得选项C中的图
形是轴对称图形.
故选C
7.B
【解析】∵MF∥AD,FN∥DC,∠A=120°,∠C=80°,
∴∠BMF=120°,∠FNB=80°,
∵将△BMN沿MN翻折得△FMN,
∴∠FMN=∠BMN=60°,∠FNM=∠MNB=40°,
∴∠F=∠B=180°-60°-40°=80°,
故选B.
8.A
【解析】如图,
点false是点A关于直线a的对称点,连接false,则false与直线a的交点即为点P,此时false最短.
∵false与直线a交于点C,
∴点P的位置应选在C点.
故选:A.
9.false
【解析】点坐标关于y轴对称的变换规律:横坐标互为相反数,纵坐标不变,
则点false关于y轴对称的点的坐标是false,
故答案为:false.
10.9:30
【解析】从镜子中看到一钟表的时针和分针,此时的实际时刻是9:30,
故答案为:9:30.
11.第2个图案. 6
【解析】解:根据轴对称图形的定义可知,第2个图案为轴对称图形,
对称轴如图所示:共有6条对称轴
故答案为:第2个图案;6.
12.100 5
【解析】解:连接CD交MN于H,如图,
∵点C和点D关于直线MN对称,
∴MN垂直平分CD,
∴CE=DE=5cm,
∴EH平分∠CED,
∴∠DEH=∠CEH=80°,
∴∠DEN=180°-80°=100°.
故答案为:100,5.
13.3
【解析】∵直线false是三角形false的对称轴,∴false垂直平分false,即false,false,
∴false,
∴false.
故答案为3.
14.(3)(4)
【解析】(1)不是轴对称图形,不符合题意;
(2)不是轴对称图形,不符合题意;
(3)是轴对称图形,符合题意;
(4)是轴对称图形,符合题意;
故答案为:(3)(4).
15.M17936
【解析】本题是轴对称中的镜面对称问题,水面相当于一个平面镜,因为镜面对称的性质是在平面镜中的像与现实中的事物恰好顺序颠倒,且关于镜面对称.故答案为.
16.15:01或10:51.
【解析】解:∵没说明平面镜在电子钟的相对位置,
∴有两种可能,
当平面镜是在电子钟的下方,则原来的实际时间是15:01;
当平面镜是在电子钟的左侧,则原来的实际时间是10:51,
故答案为:15:01或10:51.
17.见解析
【解析】解:对称轴如图所示:
18.120+85=205
【解析】由题意可知,该算式的实际情况是:120+85=205.
19.见解析
【解析】①连接false交false于点false,点false就是所求的点;
②画出点false关于直线false的对称点false,连接false交false于点false,连接false,
false、false关于直线false对称,
false,
false,
由两点之间线段最短可知,线段false的长即为false的最小值,故false点即为所求点.
20.图中有阴影的三角形与三角形1,3成轴对称;整个图形是轴对称图形;它共有2条对称轴
【解析】解:图中有阴影的三角形与三角形1、3成轴对称,
整个图形是轴对称图形,
它共有2条对称轴.
21.见解析
【解析】沿着镜面反射即可,如图所示.
22.false
【解析】false
false
false
false
23.见解析
【解析】解:作点P关于直线AC的对称点P′,连接MP′交直线AC于点N,则PN=P′N,
由于△PMN的周长=PM+MN+PN,而PM是定值,故只需在在AC上找一点N,使MN+PN最小即可;
∵此时MN+PN=MN+P′N=MP′,MN+PN最小,
∴此时△PMN的周长最小,最小值等于PM+P′M.
24.(1)画图正确 2分
(2)①利用有刻度的直尺,在∠AOB的边OA、OB上分别截取OC、OD,使OC=OD;
②连接CD,量出CD的长,画出线段CD的中点E;
③画直线OE,直线OE即为∠AOB的对称轴. 6分
(作图正确2分,作法正确2分)
【解析】(1)
;(2分)
(2)
.(4分)
画图方法:
<1>利用有刻度的直尺,在∠AOB的边OA、OB上分别截取OC、OD,使OC=OD;
<2>连接CD,量出CD的长,将线段CD二等分,画出线段CD的中点E;
<3>画直线OE,直线OE即为∠AOB的对称轴.(6分)
2.2轴对称的性质
一、单选题
1.分别以直线false为对称轴,所作轴对称图形错误的是( )
A.B.C.D.
2.已知点A(2,false)关于x轴对称的点的坐标为点B(false,false),则false的值为( )
A.-5 B.-1 C.1 D.5
3.横撇竖捺,构架成一个个文字,在下列表示生肖的方块字中,是轴对称图形的是( )
A. B. C. D.
4.如图,直线false是多边形false的对称轴,false,false,那么false( )
A.false B.false C.false D.false
5.如图,△ABC与△A′B′C′关于直线MN对称,P为MN上任一点(A、P、A′不共线),下列结论中错误的是( )
A.△AA′P是等腰三角形 B.MN垂直平分AA′、CC′
C.△ABC与△A′B′C′面积相等 D.直线AB,A′B′的交点不一定在直线MN上
6.如图所示,哪一个选项中的左边图形与右边图形成轴对称( )
A. B. C. D.
7.如图,在四边形ABCD中,∠A=120°,∠C=80°.将△BMN沿着MN翻折,得到△FMN.若MF∥AD,FN∥DC,则∠F的度数为( )
A.70° B.80° C.90° D.100°
8.如图,在false的正方形网格中,有A,B两点,在直线a上求一点P,使false最短,则点P的位置应选在( )
A.C点 B.D点 C.E点 D.F点
二、填空题
9.点false关于y轴对称的点的坐标是______.
10.如图,从镜子中看到一钟表为2:30,此时的实际时刻是___________.
11.观察图中的两个图案,是轴对称图形的是______,它有______条对称轴.
12.如图,点false在直线false上,点false和点false关于直线false对称,若false,false,则false__false,false__false.
13.如图,直线false是三角形false的对称轴,点false,false是线段false上的两点.若false,false,则图中阴影部分的面积是________.
14.如图所示的false组图形中,左、右两个图形成轴对称的是第_________________组.
15.一个汽车牌在水中的倒影为,则该车牌照号码___________.
16.下图是小明在平面镜里看到的电子钟示数,这时的实际时间是________.
三、解答题
17.如图所示的五角星共有几条对称轴?请你在下图中分别画出来.
18.如图所示的是在一面镜子里看到的一个算式,该算式的实际情况是怎样的?
19.在公路false上建筑一车站false,使它到false、false两村庄的距离和最短.(保留画图痕迹)
20.图中有阴影的三角形与哪些三角形成轴对称,整个图形是轴对称图形吗,它共有几条对称轴?
21.小强用火柴棒在桌上摆了一个不正确的等式,如图所示,你有没有什么办法,在不移动火柴棒的情况下,使桌面出现一个正确的等式?
22.如图,false中,false ,将其折叠,使点false落在边false上false处,折痕为false ,求false 的度数.
23.如图,false、false分别是false的边false、false上的点,在false上求作一点false,使false的周长最小,并说明你这样作的理由.
24.只利用一把有刻度的直尺,用度量的方法按下列要求画图:
(1)在图①中用下面的方法画等腰三角形ABC的对称轴.
①量出底边BC的长度,将线段BC二等分,即画出BC的中点D;
②画直线AD,即画出等腰三角形ABC的对称轴.
(2)在图②中画∠AOB的对称轴,并写出画图的方法.
参考答案
1.C
【解析】根据轴对称的定义可知C中图形沿直线false对折后直线false两旁的部分不能重合,
故选C.
2.B
【解析】因为点A关于x轴对称所以false=2,false=3可解得m=1,n=2, false=1-2=-1
故选:B
3.D
【解析】解:根据轴对称图形的定义知:
为轴对称图形,其它选项不符合题意.
故选:D.
4.C
【解析】解:根据题意:直线m是多边形ABCDEFGH的对称轴,BC∥AD∥m,∠B=130°,
那么∠GHA=(6×180°-4×130°)÷4=140°.
故选:C.
5.D
【解析】解:∵△ABC与△A′B′C′关于直线MN对称,P为MN上任意一点,
∴△AA′P是等腰三角形,MN垂直平分AA′,CC′,这两个三角形的面积相等,故A、B、C选项正确,
直线AB,A′B′关于直线MN对称,因此交点一定在MN上,故D错误,
故选:D.
6.C
【解析】根据轴对称图形的定义即判断方法可得选项C中的图
形是轴对称图形.
故选C
7.B
【解析】∵MF∥AD,FN∥DC,∠A=120°,∠C=80°,
∴∠BMF=120°,∠FNB=80°,
∵将△BMN沿MN翻折得△FMN,
∴∠FMN=∠BMN=60°,∠FNM=∠MNB=40°,
∴∠F=∠B=180°-60°-40°=80°,
故选B.
8.A
【解析】如图,
点false是点A关于直线a的对称点,连接false,则false与直线a的交点即为点P,此时false最短.
∵false与直线a交于点C,
∴点P的位置应选在C点.
故选:A.
9.false
【解析】点坐标关于y轴对称的变换规律:横坐标互为相反数,纵坐标不变,
则点false关于y轴对称的点的坐标是false,
故答案为:false.
10.9:30
【解析】从镜子中看到一钟表的时针和分针,此时的实际时刻是9:30,
故答案为:9:30.
11.第2个图案. 6
【解析】解:根据轴对称图形的定义可知,第2个图案为轴对称图形,
对称轴如图所示:共有6条对称轴
故答案为:第2个图案;6.
12.100 5
【解析】解:连接CD交MN于H,如图,
∵点C和点D关于直线MN对称,
∴MN垂直平分CD,
∴CE=DE=5cm,
∴EH平分∠CED,
∴∠DEH=∠CEH=80°,
∴∠DEN=180°-80°=100°.
故答案为:100,5.
13.3
【解析】∵直线false是三角形false的对称轴,∴false垂直平分false,即false,false,
∴false,
∴false.
故答案为3.
14.(3)(4)
【解析】(1)不是轴对称图形,不符合题意;
(2)不是轴对称图形,不符合题意;
(3)是轴对称图形,符合题意;
(4)是轴对称图形,符合题意;
故答案为:(3)(4).
15.M17936
【解析】本题是轴对称中的镜面对称问题,水面相当于一个平面镜,因为镜面对称的性质是在平面镜中的像与现实中的事物恰好顺序颠倒,且关于镜面对称.故答案为.
16.15:01或10:51.
【解析】解:∵没说明平面镜在电子钟的相对位置,
∴有两种可能,
当平面镜是在电子钟的下方,则原来的实际时间是15:01;
当平面镜是在电子钟的左侧,则原来的实际时间是10:51,
故答案为:15:01或10:51.
17.见解析
【解析】解:对称轴如图所示:
18.120+85=205
【解析】由题意可知,该算式的实际情况是:120+85=205.
19.见解析
【解析】①连接false交false于点false,点false就是所求的点;
②画出点false关于直线false的对称点false,连接false交false于点false,连接false,
false、false关于直线false对称,
false,
false,
由两点之间线段最短可知,线段false的长即为false的最小值,故false点即为所求点.
20.图中有阴影的三角形与三角形1,3成轴对称;整个图形是轴对称图形;它共有2条对称轴
【解析】解:图中有阴影的三角形与三角形1、3成轴对称,
整个图形是轴对称图形,
它共有2条对称轴.
21.见解析
【解析】沿着镜面反射即可,如图所示.
22.false
【解析】false
false
false
false
23.见解析
【解析】解:作点P关于直线AC的对称点P′,连接MP′交直线AC于点N,则PN=P′N,
由于△PMN的周长=PM+MN+PN,而PM是定值,故只需在在AC上找一点N,使MN+PN最小即可;
∵此时MN+PN=MN+P′N=MP′,MN+PN最小,
∴此时△PMN的周长最小,最小值等于PM+P′M.
24.(1)画图正确 2分
(2)①利用有刻度的直尺,在∠AOB的边OA、OB上分别截取OC、OD,使OC=OD;
②连接CD,量出CD的长,画出线段CD的中点E;
③画直线OE,直线OE即为∠AOB的对称轴. 6分
(作图正确2分,作法正确2分)
【解析】(1)
;(2分)
(2)
.(4分)
画图方法:
<1>利用有刻度的直尺,在∠AOB的边OA、OB上分别截取OC、OD,使OC=OD;
<2>连接CD,量出CD的长,将线段CD二等分,画出线段CD的中点E;
<3>画直线OE,直线OE即为∠AOB的对称轴.(6分)
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
