2.3确定圆的条件 一课一练 2021-2022学年苏科版九年级 上册 数学(Word版 含答案)
文档属性
| 名称 | 2.3确定圆的条件 一课一练 2021-2022学年苏科版九年级 上册 数学(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 500.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-30 00:00:00 | ||
图片预览


文档简介
(苏科版)2021-2022学年九年级(上册)数学一课一练
2.3确定圆的条件
一、单选题
1.有下列四个命题,其中正确的有( )
①圆的对称轴是直径;??????????????????????②经过三个点一定可以作圆;
③三角形的外心到三角形各顶点的距离都相等;④半径相等的两个半圆是等弧.
A.4个 B.3个 C.2个 D.1个
2.如图,点A、B、C在同一直线上,点D在直线AB之外,过这四个点中的任意三个点,能画圆的个数为( )
A.1个 B.2个 C.3个 D.4个
3.在同一平面内,过已知A,B,C三个点可以作的圆的个数为(? ? )
A.0 B.1 C.2 D.0或1
4.坐标网格中一段圆弧经过格点A、B、C.其中点B的坐标为(4,3), 点C坐标为(6,1),则该圆弧所在圆的圆心坐标为
A.(0,0) B.(2,-1) C.(0,1) D.(2,1)
5.已知AB=7cm,则过点A,B,且半径为3cm的圆有( )
A.0个 B.1个 C.2个 D.无数个
6.如图2,在平面直角坐标系中,点false的坐标为(1,4)、(5,4)、(1、false),则false外接圆的圆心坐标是
A.(2,3) B.(3,2) C.(1,3) D.(3,1)
7.如图,每个小正方形的边长为1,格点A、B、C在同一圆弧上,若点A的坐标为(﹣2,3),则该圆弧所在圆的圆心坐标是( )
A.(﹣1,1) B.(﹣3,0) C.(﹣3,1) D.(0,1)
8.如图,false、false为⊙O的切线,切点分别为A、B,false交false于点C,false的延长线交⊙O于点D.下列结论不一定成立的是( )
A.false为等腰三角形 B.false与false相互垂直平分
C.点A、B都在以false为直径的圆上 D.false为false的边false上的中线
二、填空题
9.已知:false,求作false的外接圆,作法:①分别作线段BC,AC的垂直平分线EF和MN,它们交于点O;②以点O为圆心,OB的长为半径画弧,如图⊙O即为所求,以上作图用到的数学依据是___________________.
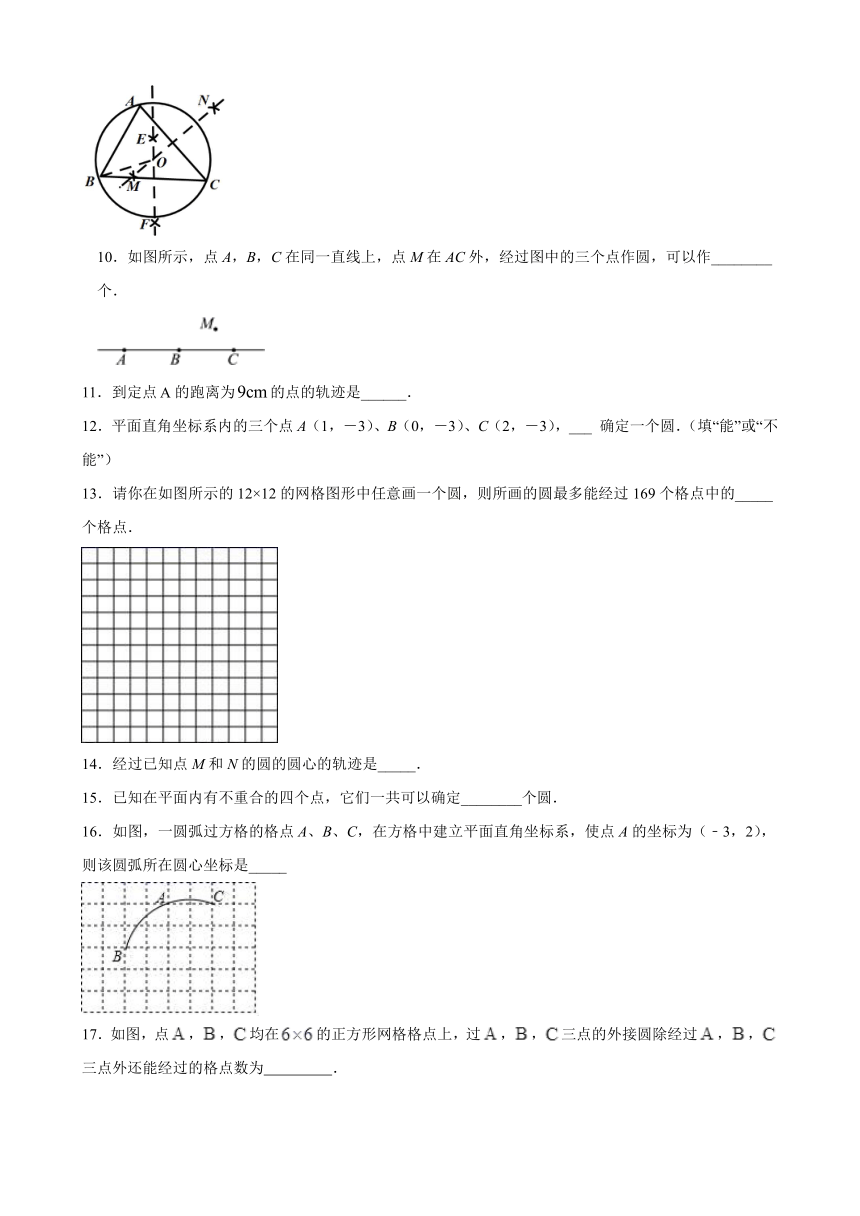
10.如图所示,点A,B,C在同一直线上,点M在AC外,经过图中的三个点作圆,可以作________个.
11.到定点false的跑离为false的点的轨迹是______.
12.平面直角坐标系内的三个点A(1,-3)、B(0,-3)、C(2,-3),___ 确定一个圆.(填“能”或“不能”)
13.请你在如图所示的12×12的网格图形中任意画一个圆,则所画的圆最多能经过169个格点中的_____个格点.
14.经过已知点M和N的圆的圆心的轨迹是_____.
15.已知在平面内有不重合的四个点,它们一共可以确定________个圆.
16.如图,一圆弧过方格的格点A、B、C,在方格中建立平面直角坐标系,使点A的坐标为(﹣3,2),则该圆弧所在圆心坐标是_____
17.如图,点,,均在的正方形网格格点上,过,,三点的外接圆除经过,,三点外还能经过的格点数为 .
三、解答题
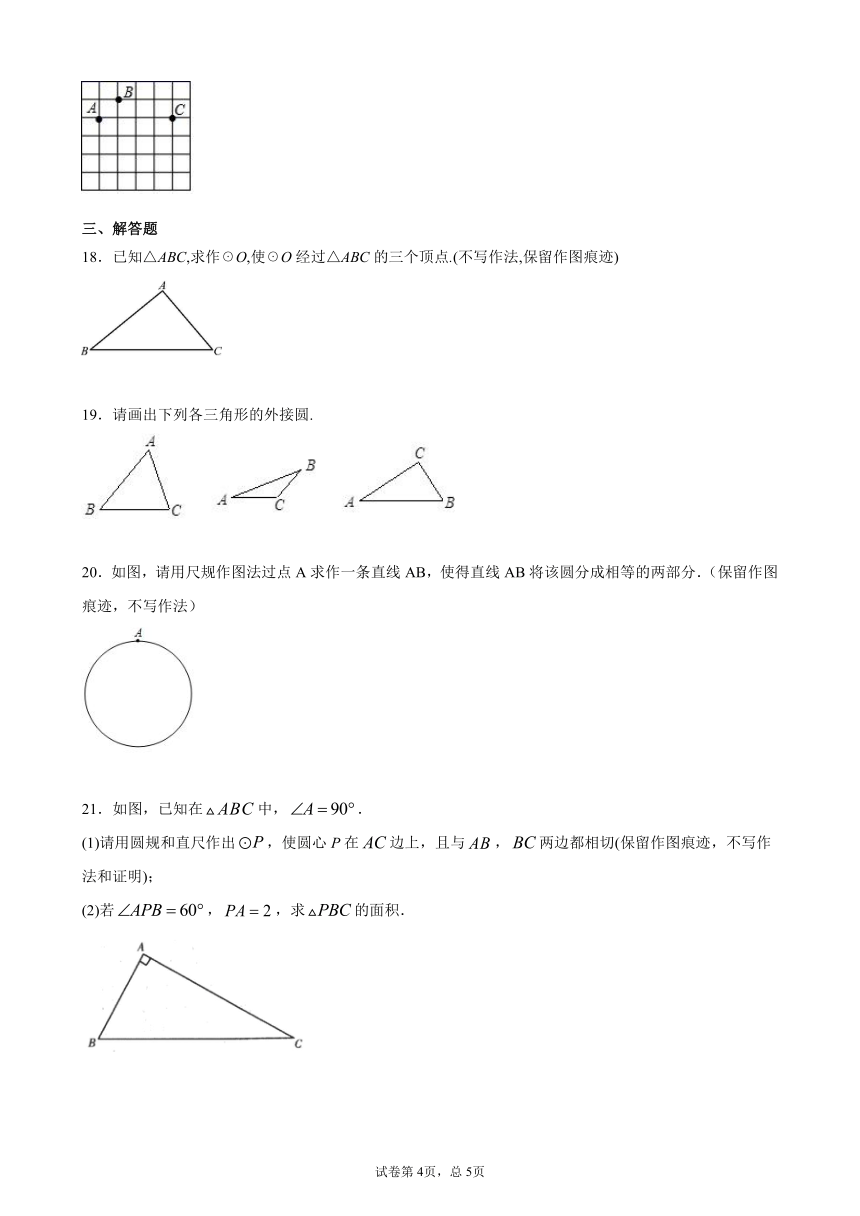
18.已知△ABC,求作☉O,使☉O经过△ABC的三个顶点.(不写作法,保留作图痕迹)
19.请画出下列各三角形的外接圆.
20.如图,请用尺规作图法过点A求作一条直线AB,使得直线AB将该圆分成相等的两部分.(保留作图痕迹,不写作法)
21.如图,已知在false中,false.
(1)请用圆规和直尺作出false,使圆心P在false边上,且与false,false两边都相切(保留作图痕迹,不写作法和证明);
(2)若false,false,求false的面积.
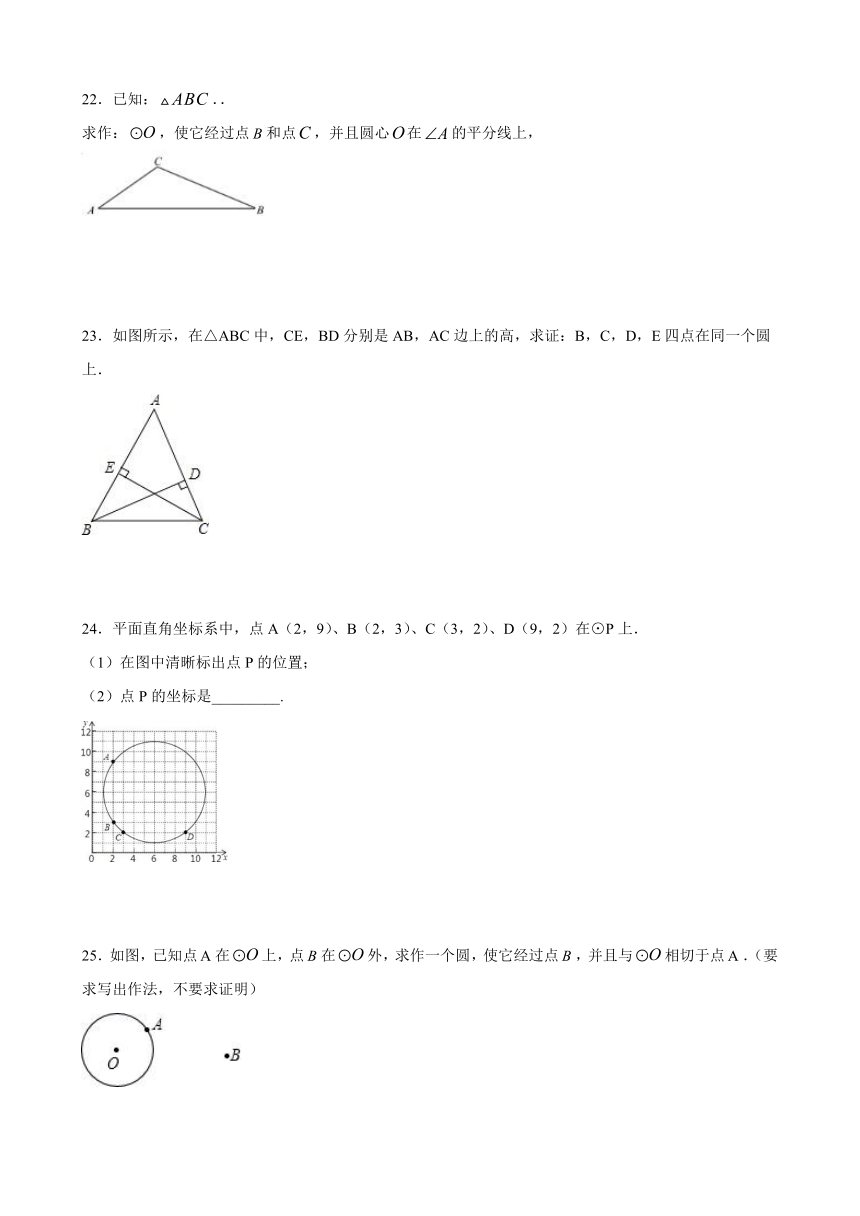
22.已知:false..
求作:false,使它经过点false和点false,并且圆心false在false的平分线上,
23.如图所示,在△ABC中,CE,BD分别是AB,AC边上的高,求证:B,C,D,E四点在同一个圆上.
24.平面直角坐标系中,点A(2,9)、B(2,3)、C(3,2)、D(9,2)在⊙P上.
(1)在图中清晰标出点P的位置;
(2)点P的坐标是_________.
25.如图,已知点false在false上,点false在false外,求作一个圆,使它经过点false,并且与false相切于点false.(要求写出作法,不要求证明)
参考答案
1.C
【解析】此题考查了圆中的有关概念:弦、直径、等弧.注意:不在同一条直线上的三个点确定一个圆.
2.C
【解析】根据题意得出:点D、A、B;点D、A、C;点D、B、C可以确定一个圆.故过这四点中的任意3个点,能画圆的个数是3个.故选C.
3.D
【解析】解:当A、B、C三个点共线,过A、B、C三个点不能作圆;
当A、B、C不在同一条直线上,过A、B、C三个点的圆有且只有一个,即三角形的外接圆;
故选D.
4.B
【解析】如图,根据已知点的坐标画出平面直角坐标系,连接BC,线段AB的垂直平分线EF交BC的垂直平分线于Q,则Q为圆弧的圆心,∴圆心的坐标是(2,-1).故选B.
5.A
【解析】∵直径R=6cm,R∴这样的圆不存在.
故选A.
6.D
【解析】解:根据垂径定理的推论,则
作弦AB、AC的垂直平分线,交点O1即为圆心,且坐标是(3,1).
故选D.
7.B
【分析】
连接AC,作出AB、AC的垂直平分线,其交点即为圆心.
【解析】如图所示,
连接AC,作出AB、AC的垂直平分线,其交点即为圆心.
∵点A的坐标为(-2,3),
∴该圆弧所在圆的圆心坐标是(-3,0).
故选:B.
8.B
【解析】解:连接OB,OC,令M为OP中点,连接MA,MB,
∵B,C为切点,
∴∠OBP=∠OAP=90°,
∵OA=OB,OP=OP,
∴Rt△OPB≌Rt△OPA,
∴BP=AP,∠OPB=∠OPA,∠BOC=∠AOC,
∴false为等腰三角形,故A正确;
∵△OBP与△OAP为直角三角形,OP为斜边,
∴PM=OM=BM=AM
∴点A、B都在以false为直径的圆上,故C正确;
∵∠BOC=∠AOC,OB=OA,OC=OC,
∴△OBC≌△OAC,
∴∠OCB=∠OCA=90°,
∴PC⊥AB,
∵△BPA为等腰三角形,
∴false为false的边false上的中线,故D正确;
无法证明false与false相互垂直平分,
故选:B.
9.线段的垂直平分线的性质
【解析】解:如图,连接false,
∵点O为AC和BC的垂直平分线的交点,
∴OA=OC=OB,
∴⊙O为false的外接圆.
故答案为:线段的垂直平分线的性质.
10.3
【解析】过A、B、M;A、C、M;B、C、M共能确定3个圆,
故答案为3.
11.以点false为圆心,false为半径的圆
【解析】到定点A的距离为9cm的点的轨迹是:以A为圆心,以9cm为半径的圆.
故答案是:以A为圆心,以9cm为半径的圆.
12.不能
【解析】解:∵B(0,-3)、C(2,-3),
∴BC∥x轴,
而点A(1,-3)与C、B共线,
∴点A、B、C共线,
∴三个点A(1,-3)、B(0,-3)、C(2,-3)不能确定一个圆.
故答案为:不能.
13.16
【解析】解:以一个小正方形的中心为圆心.记圆心坐标为(0.5,0.5),取半径为1302,此圆经过(6,2),(5,4),(4,5),(2,6),(﹣1,6),(﹣3,5),(﹣4,4),(﹣5,2),(﹣5,﹣1),(﹣4,﹣3),(﹣3,﹣4),(﹣1,5),(2,﹣5),(4,﹣4),(5,﹣3),(6,﹣1),共16个格点.
故答案为:16
14.线段MN的垂直平分线.
【解析】解:根据同圆的半径相等,则圆心应满足到点M和点N的距离相等,即经过已知点M和点N的圆的圆心的轨迹是线段MN的垂直平分线.
故答案为线段MN的垂直平分线.
15.false或false或false或false
【解析】分三种情况讨论:(1)若四点共线,则过其中三点作圆,可作0个圆;
(2)若有三点共线,则过其中三点作圆,可作3圆;
(3)若任意三点不共线,则过其中三点作圆,可作1或4个圆.
故答案为:0,1,3或4.
16.(﹣2,﹣1)
【解析】如图:分别作AC与AB的垂直平分线,相交于点O,
则点O即是该圆弧所在圆的圆心.
∵点A的坐标为(﹣3,2),∴点O的坐标为(﹣2,﹣1).
17.5.
【解析】根据圆的确定先做出过A,B,C三点的外接圆,从而得出答案.
如图,分别作AB、BC的中垂线,两直线的交点为O,
以O为圆心、OA为半径作圆,则⊙O即为过A,B,C三点的外接圆,
由图可知,⊙O还经过点D、E、F、G、H这5个格点,
故答案为5.
18.详见解析.
【解析】解:如图所示.
19.见解析
【解析】
20.见解析
【解析】①以A为圆心,任意长为半径画小圆false,与大圆交于两点C、D;
②分别以这C、D为圆心,大于falseCD的距离为半径作弧,交于点B;
③连接点AB,即可将圆分为相等的两部分,
∴AB即为所求.
如图所示:
.
21.(1)见解析;(2)false
【解析】解:(1)如图所示,则false为所求作的图.
(2)设false与false相切于点false,连接false,则false.
false
false
false
false
false
false
false
22.见详解.
【解析】解:根据题意可知,先作∠A的角平分线,
再作线段BC的垂直平分线相交于O,
即以O点为圆心,OB为半径,作圆O,
如下图所示:
23.证明见解析
【解析】证明:如图所示,取BC的中点F,连接DF,EF.
∵BD,CE是△ABC的高,
∴△BCD和△BCE都是直角三角形.
∴DF,EF分别为Rt△BCD和Rt△BCE斜边上的中线,
∴DF=EF=BF=CF.
∴E,B,C,D四点在以F点为圆心, BC为半径的圆上.
24.(1)见解析;(2)(6,6).
【解析】解:弦AB的垂直平分线是y=6,弦CD的垂直平分线是x=6,
因而交点P的坐标是(6,6).
25.见解析
【解析】解:如图,
①连接false、false,
②作线段false的垂直平分线交false的延长线于一点,交点即为false,
③以false为圆心,false或false的长度为半径作圆,
④false即为所求.
2.3确定圆的条件
一、单选题
1.有下列四个命题,其中正确的有( )
①圆的对称轴是直径;??????????????????????②经过三个点一定可以作圆;
③三角形的外心到三角形各顶点的距离都相等;④半径相等的两个半圆是等弧.
A.4个 B.3个 C.2个 D.1个
2.如图,点A、B、C在同一直线上,点D在直线AB之外,过这四个点中的任意三个点,能画圆的个数为( )
A.1个 B.2个 C.3个 D.4个
3.在同一平面内,过已知A,B,C三个点可以作的圆的个数为(? ? )
A.0 B.1 C.2 D.0或1
4.坐标网格中一段圆弧经过格点A、B、C.其中点B的坐标为(4,3), 点C坐标为(6,1),则该圆弧所在圆的圆心坐标为
A.(0,0) B.(2,-1) C.(0,1) D.(2,1)
5.已知AB=7cm,则过点A,B,且半径为3cm的圆有( )
A.0个 B.1个 C.2个 D.无数个
6.如图2,在平面直角坐标系中,点false的坐标为(1,4)、(5,4)、(1、false),则false外接圆的圆心坐标是
A.(2,3) B.(3,2) C.(1,3) D.(3,1)
7.如图,每个小正方形的边长为1,格点A、B、C在同一圆弧上,若点A的坐标为(﹣2,3),则该圆弧所在圆的圆心坐标是( )
A.(﹣1,1) B.(﹣3,0) C.(﹣3,1) D.(0,1)
8.如图,false、false为⊙O的切线,切点分别为A、B,false交false于点C,false的延长线交⊙O于点D.下列结论不一定成立的是( )
A.false为等腰三角形 B.false与false相互垂直平分
C.点A、B都在以false为直径的圆上 D.false为false的边false上的中线
二、填空题
9.已知:false,求作false的外接圆,作法:①分别作线段BC,AC的垂直平分线EF和MN,它们交于点O;②以点O为圆心,OB的长为半径画弧,如图⊙O即为所求,以上作图用到的数学依据是___________________.
10.如图所示,点A,B,C在同一直线上,点M在AC外,经过图中的三个点作圆,可以作________个.
11.到定点false的跑离为false的点的轨迹是______.
12.平面直角坐标系内的三个点A(1,-3)、B(0,-3)、C(2,-3),___ 确定一个圆.(填“能”或“不能”)
13.请你在如图所示的12×12的网格图形中任意画一个圆,则所画的圆最多能经过169个格点中的_____个格点.
14.经过已知点M和N的圆的圆心的轨迹是_____.
15.已知在平面内有不重合的四个点,它们一共可以确定________个圆.
16.如图,一圆弧过方格的格点A、B、C,在方格中建立平面直角坐标系,使点A的坐标为(﹣3,2),则该圆弧所在圆心坐标是_____
17.如图,点,,均在的正方形网格格点上,过,,三点的外接圆除经过,,三点外还能经过的格点数为 .
三、解答题
18.已知△ABC,求作☉O,使☉O经过△ABC的三个顶点.(不写作法,保留作图痕迹)
19.请画出下列各三角形的外接圆.
20.如图,请用尺规作图法过点A求作一条直线AB,使得直线AB将该圆分成相等的两部分.(保留作图痕迹,不写作法)
21.如图,已知在false中,false.
(1)请用圆规和直尺作出false,使圆心P在false边上,且与false,false两边都相切(保留作图痕迹,不写作法和证明);
(2)若false,false,求false的面积.
22.已知:false..
求作:false,使它经过点false和点false,并且圆心false在false的平分线上,
23.如图所示,在△ABC中,CE,BD分别是AB,AC边上的高,求证:B,C,D,E四点在同一个圆上.
24.平面直角坐标系中,点A(2,9)、B(2,3)、C(3,2)、D(9,2)在⊙P上.
(1)在图中清晰标出点P的位置;
(2)点P的坐标是_________.
25.如图,已知点false在false上,点false在false外,求作一个圆,使它经过点false,并且与false相切于点false.(要求写出作法,不要求证明)
参考答案
1.C
【解析】此题考查了圆中的有关概念:弦、直径、等弧.注意:不在同一条直线上的三个点确定一个圆.
2.C
【解析】根据题意得出:点D、A、B;点D、A、C;点D、B、C可以确定一个圆.故过这四点中的任意3个点,能画圆的个数是3个.故选C.
3.D
【解析】解:当A、B、C三个点共线,过A、B、C三个点不能作圆;
当A、B、C不在同一条直线上,过A、B、C三个点的圆有且只有一个,即三角形的外接圆;
故选D.
4.B
【解析】如图,根据已知点的坐标画出平面直角坐标系,连接BC,线段AB的垂直平分线EF交BC的垂直平分线于Q,则Q为圆弧的圆心,∴圆心的坐标是(2,-1).故选B.
5.A
【解析】∵直径R=6cm,R
故选A.
6.D
【解析】解:根据垂径定理的推论,则
作弦AB、AC的垂直平分线,交点O1即为圆心,且坐标是(3,1).
故选D.
7.B
【分析】
连接AC,作出AB、AC的垂直平分线,其交点即为圆心.
【解析】如图所示,
连接AC,作出AB、AC的垂直平分线,其交点即为圆心.
∵点A的坐标为(-2,3),
∴该圆弧所在圆的圆心坐标是(-3,0).
故选:B.
8.B
【解析】解:连接OB,OC,令M为OP中点,连接MA,MB,
∵B,C为切点,
∴∠OBP=∠OAP=90°,
∵OA=OB,OP=OP,
∴Rt△OPB≌Rt△OPA,
∴BP=AP,∠OPB=∠OPA,∠BOC=∠AOC,
∴false为等腰三角形,故A正确;
∵△OBP与△OAP为直角三角形,OP为斜边,
∴PM=OM=BM=AM
∴点A、B都在以false为直径的圆上,故C正确;
∵∠BOC=∠AOC,OB=OA,OC=OC,
∴△OBC≌△OAC,
∴∠OCB=∠OCA=90°,
∴PC⊥AB,
∵△BPA为等腰三角形,
∴false为false的边false上的中线,故D正确;
无法证明false与false相互垂直平分,
故选:B.
9.线段的垂直平分线的性质
【解析】解:如图,连接false,
∵点O为AC和BC的垂直平分线的交点,
∴OA=OC=OB,
∴⊙O为false的外接圆.
故答案为:线段的垂直平分线的性质.
10.3
【解析】过A、B、M;A、C、M;B、C、M共能确定3个圆,
故答案为3.
11.以点false为圆心,false为半径的圆
【解析】到定点A的距离为9cm的点的轨迹是:以A为圆心,以9cm为半径的圆.
故答案是:以A为圆心,以9cm为半径的圆.
12.不能
【解析】解:∵B(0,-3)、C(2,-3),
∴BC∥x轴,
而点A(1,-3)与C、B共线,
∴点A、B、C共线,
∴三个点A(1,-3)、B(0,-3)、C(2,-3)不能确定一个圆.
故答案为:不能.
13.16
【解析】解:以一个小正方形的中心为圆心.记圆心坐标为(0.5,0.5),取半径为1302,此圆经过(6,2),(5,4),(4,5),(2,6),(﹣1,6),(﹣3,5),(﹣4,4),(﹣5,2),(﹣5,﹣1),(﹣4,﹣3),(﹣3,﹣4),(﹣1,5),(2,﹣5),(4,﹣4),(5,﹣3),(6,﹣1),共16个格点.
故答案为:16
14.线段MN的垂直平分线.
【解析】解:根据同圆的半径相等,则圆心应满足到点M和点N的距离相等,即经过已知点M和点N的圆的圆心的轨迹是线段MN的垂直平分线.
故答案为线段MN的垂直平分线.
15.false或false或false或false
【解析】分三种情况讨论:(1)若四点共线,则过其中三点作圆,可作0个圆;
(2)若有三点共线,则过其中三点作圆,可作3圆;
(3)若任意三点不共线,则过其中三点作圆,可作1或4个圆.
故答案为:0,1,3或4.
16.(﹣2,﹣1)
【解析】如图:分别作AC与AB的垂直平分线,相交于点O,
则点O即是该圆弧所在圆的圆心.
∵点A的坐标为(﹣3,2),∴点O的坐标为(﹣2,﹣1).
17.5.
【解析】根据圆的确定先做出过A,B,C三点的外接圆,从而得出答案.
如图,分别作AB、BC的中垂线,两直线的交点为O,
以O为圆心、OA为半径作圆,则⊙O即为过A,B,C三点的外接圆,
由图可知,⊙O还经过点D、E、F、G、H这5个格点,
故答案为5.
18.详见解析.
【解析】解:如图所示.
19.见解析
【解析】
20.见解析
【解析】①以A为圆心,任意长为半径画小圆false,与大圆交于两点C、D;
②分别以这C、D为圆心,大于falseCD的距离为半径作弧,交于点B;
③连接点AB,即可将圆分为相等的两部分,
∴AB即为所求.
如图所示:
.
21.(1)见解析;(2)false
【解析】解:(1)如图所示,则false为所求作的图.
(2)设false与false相切于点false,连接false,则false.
false
false
false
false
false
false
false
22.见详解.
【解析】解:根据题意可知,先作∠A的角平分线,
再作线段BC的垂直平分线相交于O,
即以O点为圆心,OB为半径,作圆O,
如下图所示:
23.证明见解析
【解析】证明:如图所示,取BC的中点F,连接DF,EF.
∵BD,CE是△ABC的高,
∴△BCD和△BCE都是直角三角形.
∴DF,EF分别为Rt△BCD和Rt△BCE斜边上的中线,
∴DF=EF=BF=CF.
∴E,B,C,D四点在以F点为圆心, BC为半径的圆上.
24.(1)见解析;(2)(6,6).
【解析】解:弦AB的垂直平分线是y=6,弦CD的垂直平分线是x=6,
因而交点P的坐标是(6,6).
25.见解析
【解析】解:如图,
①连接false、false,
②作线段false的垂直平分线交false的延长线于一点,交点即为false,
③以false为圆心,false或false的长度为半径作圆,
④false即为所求.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
