2.8圆锥的侧面积 一课一练 2021-2022学年苏科版九年级 上册 数学(Word版 含答案)
文档属性
| 名称 | 2.8圆锥的侧面积 一课一练 2021-2022学年苏科版九年级 上册 数学(Word版 含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 575.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-30 00:00:00 | ||
图片预览


文档简介
(苏科版)2021-2022学年九年级(上册)数学一课一练
2.8圆锥的侧面积
一、单选题
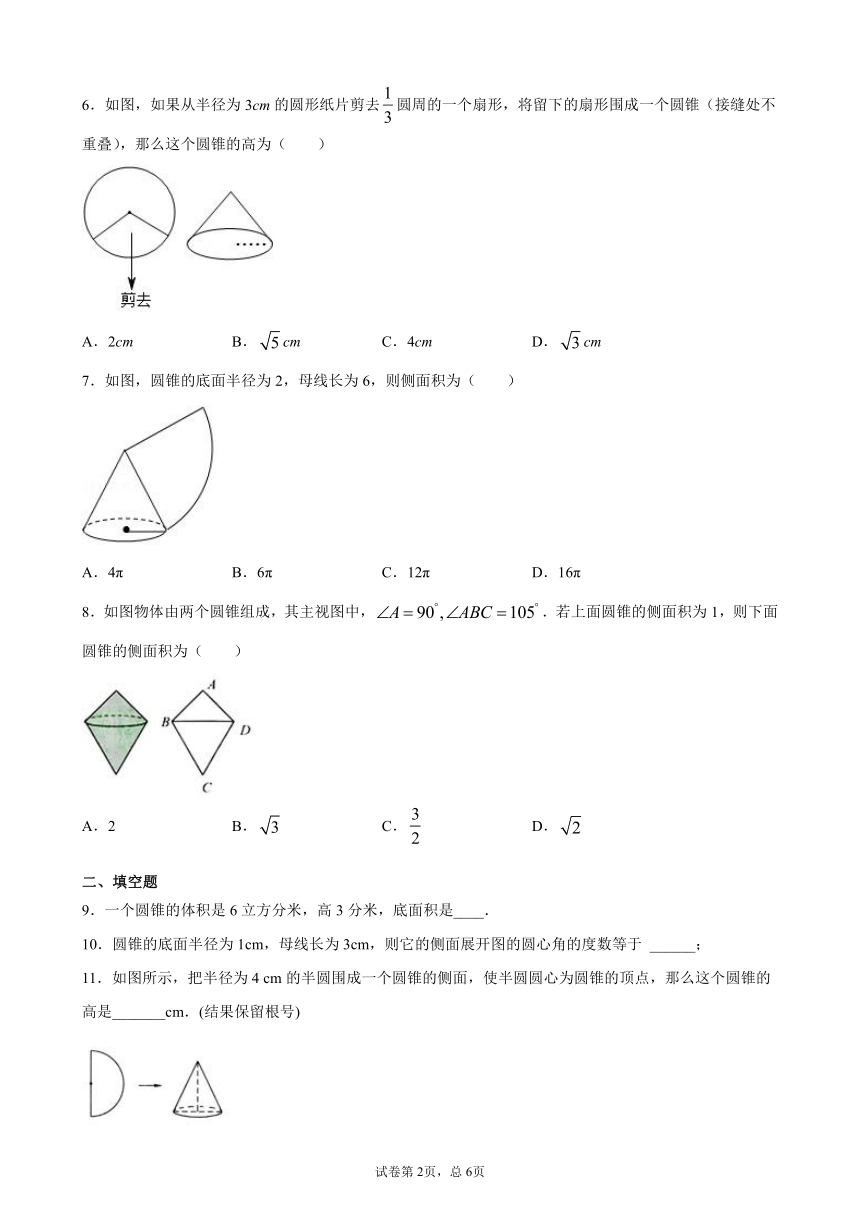
1.已知圆锥的高为4 cm,底面半径为3 cm,那么,这个圆锥的侧面展开图扇形的圆心角的度数为( );
A.180° B.200° C.216° D.225°
2.若将半径为12cm的半圆形纸片围成一个圆锥的侧面,则这个圆锥的底面圆半径是( )
A.2cm B.3cm C.4cm D.6cm
3.如图,有一圆心角为120°、半径长为false的扇形,若将false、false重合后围成一圆锥侧面,那么圆锥的高是( )
A.falsecm B.false C.false D.false
4.如图所示,圆锥底面的半径为5,母线长为20,一只蜘蛛从底面圆周上一点A出发沿圆锥的侧面爬行一周后回到点A的最短路程是( )
A.false B.false C.false D.false
5.如图,从一圆形纸片上剪出一个半径为R、圆心角为90°的扇形;和一半径为false的圆,使之恰好围成如图所示的圆锥,则R与false的关系为( )
A.R=2false B.R=4false C.R=2false D.R=6false
6.如图,如果从半径为3cm的圆形纸片剪去false圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为( )
A.2cm B.falsecm C.4cm D.falsecm
7.如图,圆锥的底面半径为2,母线长为6,则侧面积为( )
A.4π B.6π C.12π D.16π
8.如图物体由两个圆锥组成,其主视图中,false.若上面圆锥的侧面积为1,则下面圆锥的侧面积为( )
A.2 B.false C.false D.false
二、填空题
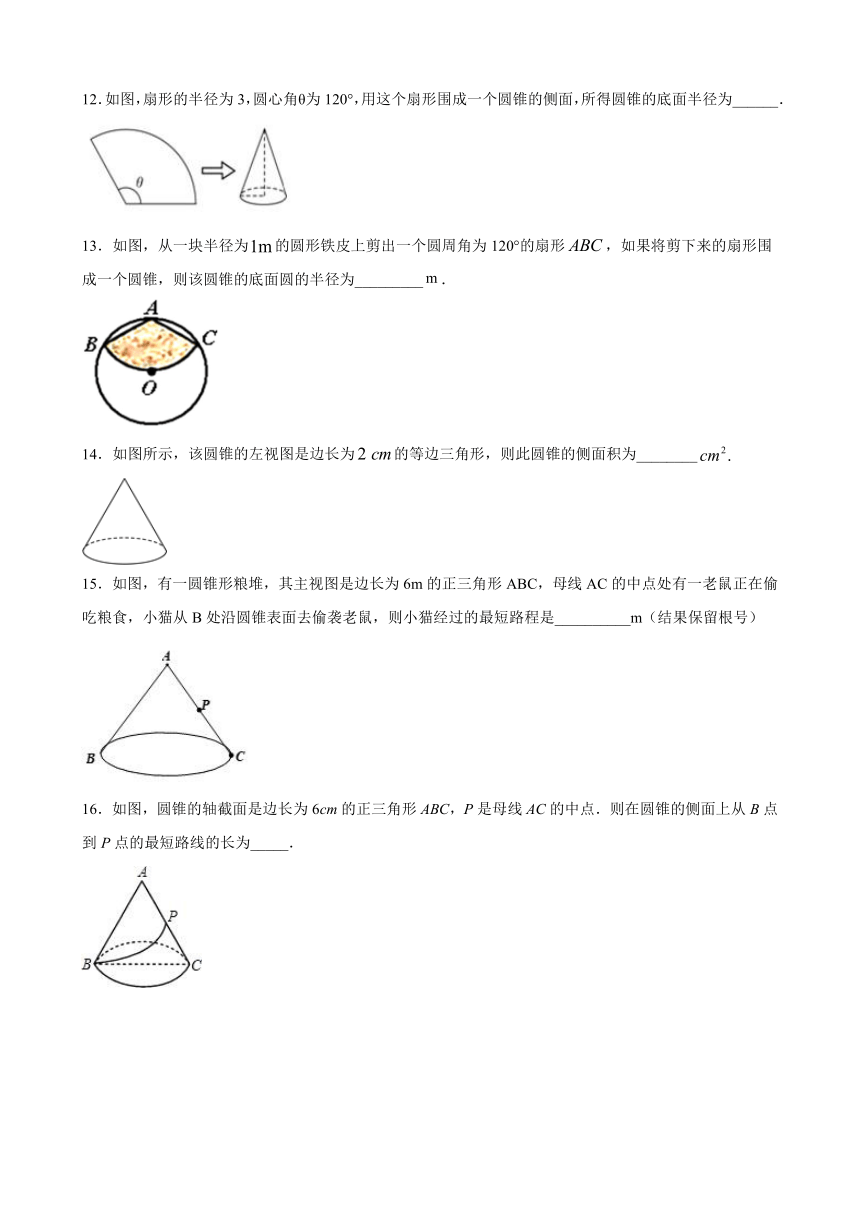
9.一个圆锥的体积是6立方分米,高3分米,底面积是____.
10.圆锥的底面半径为1cm,母线长为3cm,则它的侧面展开图的圆心角的度数等于 ______;
11.如图所示,把半径为4 cm的半圆围成一个圆锥的侧面,使半圆圆心为圆锥的顶点,那么这个圆锥的高是_______cm.(结果保留根号)
12.如图,扇形的半径为3,圆心角θ为120°,用这个扇形围成一个圆锥的侧面,所得圆锥的底面半径为______.
13.如图,从一块半径为false的圆形铁皮上剪出一个圆周角为120°的扇形false,如果将剪下来的扇形围成一个圆锥,则该圆锥的底面圆的半径为_________false.
14.如图所示,该圆锥的左视图是边长为false的等边三角形,则此圆锥的侧面积为________false
15.如图,有一圆锥形粮堆,其主视图是边长为6m的正三角形ABC,母线AC的中点处有一老鼠正在偷吃粮食,小猫从B处沿圆锥表面去偷袭老鼠,则小猫经过的最短路程是__________m(结果保留根号)
16.如图,圆锥的轴截面是边长为6cm的正三角形ABC,P是母线AC的中点.则在圆锥的侧面上从B点到P点的最短路线的长为_____.
三、解答题
17.已知圆锥的底面半径为r=20cm,高h=falsecm,现在有一只蚂蚁从底边上一点A出发.在侧面上爬行一周又回到A点,求蚂蚁爬行的最短距离.
18.如图,已知在false中,false.
(1)求点false到直线false的距离以及false的长度.
(2)将false绕线段false所在的直线旋转一周,求所得几何体的表面积.
19.把一个圆锥截成圆台,已知圆台的上、下底面半径的比是1∶4,母线长10cm.求:圆锥的母长.
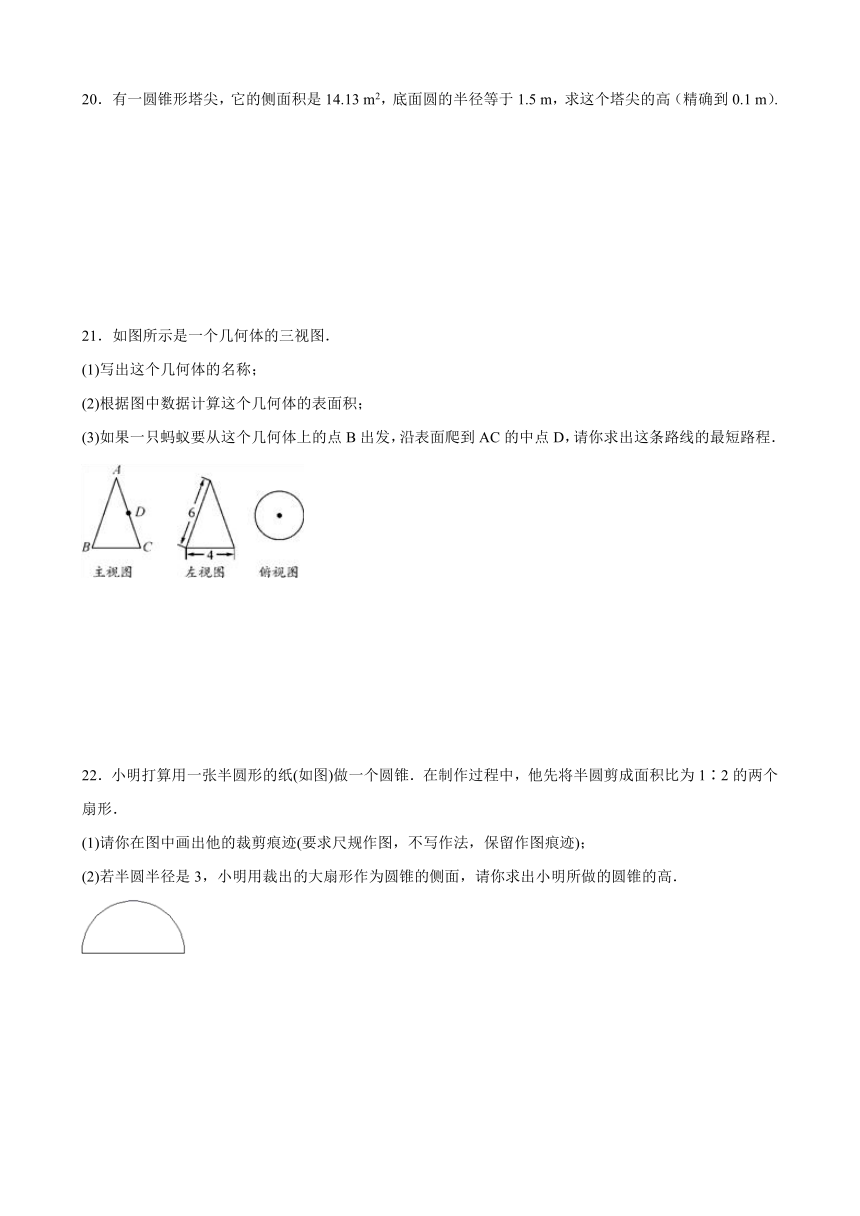
有一圆锥形塔尖,它的侧面积是14.13 m2,底面圆的半径等于1.5 m,求这个塔尖的高(精确到0.1 m).
21.如图所示是一个几何体的三视图.
(1)写出这个几何体的名称;
(2)根据图中数据计算这个几何体的表面积;
(3)如果一只蚂蚁要从这个几何体上的点B出发,沿表面爬到AC的中点D,请你求出这条路线的最短路程.
22.小明打算用一张半圆形的纸(如图)做一个圆锥.在制作过程中,他先将半圆剪成面积比为1∶2的两个扇形.
(1)请你在图中画出他的裁剪痕迹(要求尺规作图,不写作法,保留作图痕迹);
(2)若半圆半径是3,小明用裁出的大扇形作为圆锥的侧面,请你求出小明所做的圆锥的高.
23.有一个直径为1m的圆形铁皮,要从中剪出一个最大的圆心角为90°的扇形ABC,如图所示.
(1)求被剪掉阴影部分的面积:
(2)用所留的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径是多少?
24.如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:
(1)请在图中确定该圆弧所在圆心D点的位置,D点坐标为 ;
(2)连接AD、CD,则⊙D的半径为 ;扇形DAC的圆心角度数为 ;
(3)若扇形DAC是某一个圆锥的侧面展开图,求该圆锥的底面半径.
参考答案
1.C
【解析】圆锥的母线长为:false
则:false
解得false
故选:C.
2.D
【解析】解:圆锥的侧面展开图的弧长为2π×12÷2=12π(cm),∴圆锥的底面半径为12π÷2π=6(cm),故选D.
3.A
【解析】解:由圆心角为120°,半径长为6cm,
可知扇形的弧长为:falsecm,
即圆锥的底面圆周长为4πcm,
可得底面圆半径为2cm,
由勾股定理得圆锥的高是falsecm.
故选A.
4.D
【解析】圆锥的底面周长=2π×5=10π,
设侧面展开图的圆心角的度数为n.
∴false,
解得n=90,
圆锥的侧面展开图,如图所示:
∴最短路程为:false=20false,
故选D.
5.B
【解析】扇形的弧长是:false=false,
圆的半径为r,则底面圆的周长是false,
∵恰好围成如图所示的圆锥,
∴false=false,
∴R=4r,
故选:B.
6.B
【解析】解:∵从半径为3cm的圆形纸片剪去false圆周的一个扇形,
∴剩下的扇形的角度=360°×false=240°,
∴留下的扇形的弧长=false=4π,
∴圆锥的底面半径r=false=2cm,
∴圆锥的高=false=falsecm.
故选:B.
7.C
【解析】根据圆锥的侧面积公式:πrl=π×2×6=12π,
故选C.
8.D
【解析】∵∠A=90°,AB=AD,
∴△ABD为等腰直角三角形,
∴∠ABD=45°,BD=falseAB,
∵∠ABC=105°,
∴∠CBD=60°,
而CB=CD,
∴△CBD为等边三角形,
∴BC=BD=falseAB,
∵上面圆锥与下面圆锥的底面相同,
∴上面圆锥的侧面积与下面圆锥的侧面积的比等于AB:CB,
∴下面圆锥的侧面积=false×1=false.
故选D.
9.6平方分米.
【解析】解:false(平方分米).
故答案为:6平方分米.
10.120°
【解析】设圆心角为n,底面半径是1,
则底面周长false
∴false
故答案为:false
11.false
【解析】∵半径为4cm的半圆围成一个圆锥的侧面,
∴圆锥的侧面展开图的弧长为4πcm,
∴圆锥的底面周长为4πcm,
∴圆锥底面的半径为4π÷2π=2cm,
∴圆锥的高为:false .
12.1
【解析】扇形的弧长=false=2π,
∴圆锥的底面半径为2π÷2π=1.
故答案为1.
13.false
【解析】连接OA,OB,
则∠BAO=false∠BAC=false=60°,
又∵OA=OB,
∴△AOB是等边三角形,
∴AB=OA=1,
∵∠BAC=120°,
∴false的长为:false,
设圆锥底面圆的半径为r
false
false
故答案为false.
14.false
【解析】根据题意,圆锥的侧面积=false×2×2π=2π(cm2).
故答案为:false
15.3false
【解析】
根据圆锥的侧面积等于展开扇形的面积得:false,设圆锥侧面展开图圆心角为n,则false=18π,解得n=180false,展开的半个侧面的圆心角是90false(如图),
因为两点之间线段最短,则根据勾股定理得:BP=false=false(m).
16.3false.
【解析】解:圆锥底面是以BC为直径的圆,圆的周长是BCπ=6π,
以AB为一边,将圆锥展开,就得到一个以A为圆心,以AB为半径的扇形,弧长是l=6π,
设展开后的圆心角是n°,则false,
解得:n=180,
即展开后∠BAC=false×180°=90°,
AP=falseAC=3,AB=6,
则在圆锥的侧面上从B点到P点的最短路线的长就是展开后线段BP的长,
由勾股定理得:BP=false,
故答案为:false.
17.false
【解析】解:设扇形的圆心角为n,圆锥的
在Rt△AOS中,∵r=20cm,h=falsecm,
∴由勾股定理可得母线l=false=80cm,
而圆锥侧面展开后的扇形的弧长为2×20π=false.
∴n=90°
即△SAA′是等腰直角三角形,
∴由勾股定理得:AA'=false=80falsecm.
∴蚂蚁爬行的最短距离为80falsecm.
18.(1)A到BC的距离为2,BC的长度为false;(2)false
【解析】(1)如图,过点false作false于点false.
在false中,false
false.
∴点false到直线false的距离为2
在false中,
false,
false.
(2)将false绕线段false所在直线旋转一周,所得几何体的表面积为
false
false
19.圆锥的母线长为falsecm.
【解析】设圆锥的母线长为false,圆台上、下底半径为false.
false
答:圆锥的母线长为falsecm.
20.约2.6 m.
【解析】如图:
false
则圆锥的底面周长为:false
圆锥的侧面积=false
false
则这个塔尖的高false
答:这个塔尖的高约2.6 m.
21.(1)圆锥;(2)16π;(3)3false
【解析】解:(1)由该几何体的三视图可知:这个几何体是圆锥;
(2)由图中数据可知:这个圆锥的底面半径为2,母线长为6,
∴S表=S侧+S底=π r l+π r2=12π+4π=16π(cm2);
(3)如下图所示,将圆锥侧面沿AB展开,则图中线段BD′为所求最短路程.
设∠BAB′的度数为n,则由false可得:
false,解得:false,
∵点C′为false的中点,
∴∠BAC′=60°,
又∵AB=AC′,
∴△ABC′是等边三角形,
又∵D′是AC′的中点,
∴∠AD′B=90°,
∴sin∠BAD′=false,
∴BD′=AB·sin60°=6×false=false(cm),
∴蚂蚁爬行的最短路程是falsecm.
22.(1)见解析;(2)2false
【解析】解:(1)如答图所示;
(2)∵半圆的半径为3,
∴半圆的弧长为3π,
∵剪成面积比为1∶2的两个扇形.
∴大扇形的弧长为2π,
设围成的圆锥的底面半径为r,则2πr=2π,
解得r=1,
∴圆锥的高为=2.
23.(1)false平方米;(2)false米;
【解析】(1)∵∠BAC=90°
∴弦BC为直径
∴AB=AC
∴AB=AC=BC·sin45°=
∴S阴影=S⊙O-S扇形ABC=()2-;
(2)设圆锥底面圆的半径为r,而弧BC的长即为圆锥底面的周长,由题意得
2falser=false,解得r=false
答:(1)被剪掉的阴影部分的面积为;(2)该圆锥的底面圆半径是.
24.(1)(2,0);(2)2false,90;(3)false
【解析】(1)如图,分别作AB、BC的垂直平分线,两线交于点D,
∴D点的坐标为(2,0).
(2)连接DA、DC,如图,
则AD=false,
即⊙D的半径为false.
∵OD=CE,OA=DE=4,
∠AOD=∠CEO=90°,
∴△AOD≌△DEC,
∴∠OAD=∠CDE,
∴∠ADO+∠CDE=∠ADO+∠OAD=90°,
∴∠ADC=90°,
即扇形DAC的圆心角度数为90°.
(3)设圆锥的底面半径是r,
则false,
∴false,
即该圆锥的底面半径为false.
2.8圆锥的侧面积
一、单选题
1.已知圆锥的高为4 cm,底面半径为3 cm,那么,这个圆锥的侧面展开图扇形的圆心角的度数为( );
A.180° B.200° C.216° D.225°
2.若将半径为12cm的半圆形纸片围成一个圆锥的侧面,则这个圆锥的底面圆半径是( )
A.2cm B.3cm C.4cm D.6cm
3.如图,有一圆心角为120°、半径长为false的扇形,若将false、false重合后围成一圆锥侧面,那么圆锥的高是( )
A.falsecm B.false C.false D.false
4.如图所示,圆锥底面的半径为5,母线长为20,一只蜘蛛从底面圆周上一点A出发沿圆锥的侧面爬行一周后回到点A的最短路程是( )
A.false B.false C.false D.false
5.如图,从一圆形纸片上剪出一个半径为R、圆心角为90°的扇形;和一半径为false的圆,使之恰好围成如图所示的圆锥,则R与false的关系为( )
A.R=2false B.R=4false C.R=2false D.R=6false
6.如图,如果从半径为3cm的圆形纸片剪去false圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为( )
A.2cm B.falsecm C.4cm D.falsecm
7.如图,圆锥的底面半径为2,母线长为6,则侧面积为( )
A.4π B.6π C.12π D.16π
8.如图物体由两个圆锥组成,其主视图中,false.若上面圆锥的侧面积为1,则下面圆锥的侧面积为( )
A.2 B.false C.false D.false
二、填空题
9.一个圆锥的体积是6立方分米,高3分米,底面积是____.
10.圆锥的底面半径为1cm,母线长为3cm,则它的侧面展开图的圆心角的度数等于 ______;
11.如图所示,把半径为4 cm的半圆围成一个圆锥的侧面,使半圆圆心为圆锥的顶点,那么这个圆锥的高是_______cm.(结果保留根号)
12.如图,扇形的半径为3,圆心角θ为120°,用这个扇形围成一个圆锥的侧面,所得圆锥的底面半径为______.
13.如图,从一块半径为false的圆形铁皮上剪出一个圆周角为120°的扇形false,如果将剪下来的扇形围成一个圆锥,则该圆锥的底面圆的半径为_________false.
14.如图所示,该圆锥的左视图是边长为false的等边三角形,则此圆锥的侧面积为________false
15.如图,有一圆锥形粮堆,其主视图是边长为6m的正三角形ABC,母线AC的中点处有一老鼠正在偷吃粮食,小猫从B处沿圆锥表面去偷袭老鼠,则小猫经过的最短路程是__________m(结果保留根号)
16.如图,圆锥的轴截面是边长为6cm的正三角形ABC,P是母线AC的中点.则在圆锥的侧面上从B点到P点的最短路线的长为_____.
三、解答题
17.已知圆锥的底面半径为r=20cm,高h=falsecm,现在有一只蚂蚁从底边上一点A出发.在侧面上爬行一周又回到A点,求蚂蚁爬行的最短距离.
18.如图,已知在false中,false.
(1)求点false到直线false的距离以及false的长度.
(2)将false绕线段false所在的直线旋转一周,求所得几何体的表面积.
19.把一个圆锥截成圆台,已知圆台的上、下底面半径的比是1∶4,母线长10cm.求:圆锥的母长.
有一圆锥形塔尖,它的侧面积是14.13 m2,底面圆的半径等于1.5 m,求这个塔尖的高(精确到0.1 m).
21.如图所示是一个几何体的三视图.
(1)写出这个几何体的名称;
(2)根据图中数据计算这个几何体的表面积;
(3)如果一只蚂蚁要从这个几何体上的点B出发,沿表面爬到AC的中点D,请你求出这条路线的最短路程.
22.小明打算用一张半圆形的纸(如图)做一个圆锥.在制作过程中,他先将半圆剪成面积比为1∶2的两个扇形.
(1)请你在图中画出他的裁剪痕迹(要求尺规作图,不写作法,保留作图痕迹);
(2)若半圆半径是3,小明用裁出的大扇形作为圆锥的侧面,请你求出小明所做的圆锥的高.
23.有一个直径为1m的圆形铁皮,要从中剪出一个最大的圆心角为90°的扇形ABC,如图所示.
(1)求被剪掉阴影部分的面积:
(2)用所留的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径是多少?
24.如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:
(1)请在图中确定该圆弧所在圆心D点的位置,D点坐标为 ;
(2)连接AD、CD,则⊙D的半径为 ;扇形DAC的圆心角度数为 ;
(3)若扇形DAC是某一个圆锥的侧面展开图,求该圆锥的底面半径.
参考答案
1.C
【解析】圆锥的母线长为:false
则:false
解得false
故选:C.
2.D
【解析】解:圆锥的侧面展开图的弧长为2π×12÷2=12π(cm),∴圆锥的底面半径为12π÷2π=6(cm),故选D.
3.A
【解析】解:由圆心角为120°,半径长为6cm,
可知扇形的弧长为:falsecm,
即圆锥的底面圆周长为4πcm,
可得底面圆半径为2cm,
由勾股定理得圆锥的高是falsecm.
故选A.
4.D
【解析】圆锥的底面周长=2π×5=10π,
设侧面展开图的圆心角的度数为n.
∴false,
解得n=90,
圆锥的侧面展开图,如图所示:
∴最短路程为:false=20false,
故选D.
5.B
【解析】扇形的弧长是:false=false,
圆的半径为r,则底面圆的周长是false,
∵恰好围成如图所示的圆锥,
∴false=false,
∴R=4r,
故选:B.
6.B
【解析】解:∵从半径为3cm的圆形纸片剪去false圆周的一个扇形,
∴剩下的扇形的角度=360°×false=240°,
∴留下的扇形的弧长=false=4π,
∴圆锥的底面半径r=false=2cm,
∴圆锥的高=false=falsecm.
故选:B.
7.C
【解析】根据圆锥的侧面积公式:πrl=π×2×6=12π,
故选C.
8.D
【解析】∵∠A=90°,AB=AD,
∴△ABD为等腰直角三角形,
∴∠ABD=45°,BD=falseAB,
∵∠ABC=105°,
∴∠CBD=60°,
而CB=CD,
∴△CBD为等边三角形,
∴BC=BD=falseAB,
∵上面圆锥与下面圆锥的底面相同,
∴上面圆锥的侧面积与下面圆锥的侧面积的比等于AB:CB,
∴下面圆锥的侧面积=false×1=false.
故选D.
9.6平方分米.
【解析】解:false(平方分米).
故答案为:6平方分米.
10.120°
【解析】设圆心角为n,底面半径是1,
则底面周长false
∴false
故答案为:false
11.false
【解析】∵半径为4cm的半圆围成一个圆锥的侧面,
∴圆锥的侧面展开图的弧长为4πcm,
∴圆锥的底面周长为4πcm,
∴圆锥底面的半径为4π÷2π=2cm,
∴圆锥的高为:false .
12.1
【解析】扇形的弧长=false=2π,
∴圆锥的底面半径为2π÷2π=1.
故答案为1.
13.false
【解析】连接OA,OB,
则∠BAO=false∠BAC=false=60°,
又∵OA=OB,
∴△AOB是等边三角形,
∴AB=OA=1,
∵∠BAC=120°,
∴false的长为:false,
设圆锥底面圆的半径为r
false
false
故答案为false.
14.false
【解析】根据题意,圆锥的侧面积=false×2×2π=2π(cm2).
故答案为:false
15.3false
【解析】
根据圆锥的侧面积等于展开扇形的面积得:false,设圆锥侧面展开图圆心角为n,则false=18π,解得n=180false,展开的半个侧面的圆心角是90false(如图),
因为两点之间线段最短,则根据勾股定理得:BP=false=false(m).
16.3false.
【解析】解:圆锥底面是以BC为直径的圆,圆的周长是BCπ=6π,
以AB为一边,将圆锥展开,就得到一个以A为圆心,以AB为半径的扇形,弧长是l=6π,
设展开后的圆心角是n°,则false,
解得:n=180,
即展开后∠BAC=false×180°=90°,
AP=falseAC=3,AB=6,
则在圆锥的侧面上从B点到P点的最短路线的长就是展开后线段BP的长,
由勾股定理得:BP=false,
故答案为:false.
17.false
【解析】解:设扇形的圆心角为n,圆锥的
在Rt△AOS中,∵r=20cm,h=falsecm,
∴由勾股定理可得母线l=false=80cm,
而圆锥侧面展开后的扇形的弧长为2×20π=false.
∴n=90°
即△SAA′是等腰直角三角形,
∴由勾股定理得:AA'=false=80falsecm.
∴蚂蚁爬行的最短距离为80falsecm.
18.(1)A到BC的距离为2,BC的长度为false;(2)false
【解析】(1)如图,过点false作false于点false.
在false中,false
false.
∴点false到直线false的距离为2
在false中,
false,
false.
(2)将false绕线段false所在直线旋转一周,所得几何体的表面积为
false
false
19.圆锥的母线长为falsecm.
【解析】设圆锥的母线长为false,圆台上、下底半径为false.
false
答:圆锥的母线长为falsecm.
20.约2.6 m.
【解析】如图:
false
则圆锥的底面周长为:false
圆锥的侧面积=false
false
则这个塔尖的高false
答:这个塔尖的高约2.6 m.
21.(1)圆锥;(2)16π;(3)3false
【解析】解:(1)由该几何体的三视图可知:这个几何体是圆锥;
(2)由图中数据可知:这个圆锥的底面半径为2,母线长为6,
∴S表=S侧+S底=π r l+π r2=12π+4π=16π(cm2);
(3)如下图所示,将圆锥侧面沿AB展开,则图中线段BD′为所求最短路程.
设∠BAB′的度数为n,则由false可得:
false,解得:false,
∵点C′为false的中点,
∴∠BAC′=60°,
又∵AB=AC′,
∴△ABC′是等边三角形,
又∵D′是AC′的中点,
∴∠AD′B=90°,
∴sin∠BAD′=false,
∴BD′=AB·sin60°=6×false=false(cm),
∴蚂蚁爬行的最短路程是falsecm.
22.(1)见解析;(2)2false
【解析】解:(1)如答图所示;
(2)∵半圆的半径为3,
∴半圆的弧长为3π,
∵剪成面积比为1∶2的两个扇形.
∴大扇形的弧长为2π,
设围成的圆锥的底面半径为r,则2πr=2π,
解得r=1,
∴圆锥的高为=2.
23.(1)false平方米;(2)false米;
【解析】(1)∵∠BAC=90°
∴弦BC为直径
∴AB=AC
∴AB=AC=BC·sin45°=
∴S阴影=S⊙O-S扇形ABC=()2-;
(2)设圆锥底面圆的半径为r,而弧BC的长即为圆锥底面的周长,由题意得
2falser=false,解得r=false
答:(1)被剪掉的阴影部分的面积为;(2)该圆锥的底面圆半径是.
24.(1)(2,0);(2)2false,90;(3)false
【解析】(1)如图,分别作AB、BC的垂直平分线,两线交于点D,
∴D点的坐标为(2,0).
(2)连接DA、DC,如图,
则AD=false,
即⊙D的半径为false.
∵OD=CE,OA=DE=4,
∠AOD=∠CEO=90°,
∴△AOD≌△DEC,
∴∠OAD=∠CDE,
∴∠ADO+∠CDE=∠ADO+∠OAD=90°,
∴∠ADC=90°,
即扇形DAC的圆心角度数为90°.
(3)设圆锥的底面半径是r,
则false,
∴false,
即该圆锥的底面半径为false.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
