《18.2 勾股定理的逆定理 》 同步练习卷2020-2021学年沪科版八年级数学下册(Word版 含答案)
文档属性
| 名称 | 《18.2 勾股定理的逆定理 》 同步练习卷2020-2021学年沪科版八年级数学下册(Word版 含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 257.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-30 00:00:00 | ||
图片预览


文档简介
18.2 勾股定理的逆定理
一.选择题
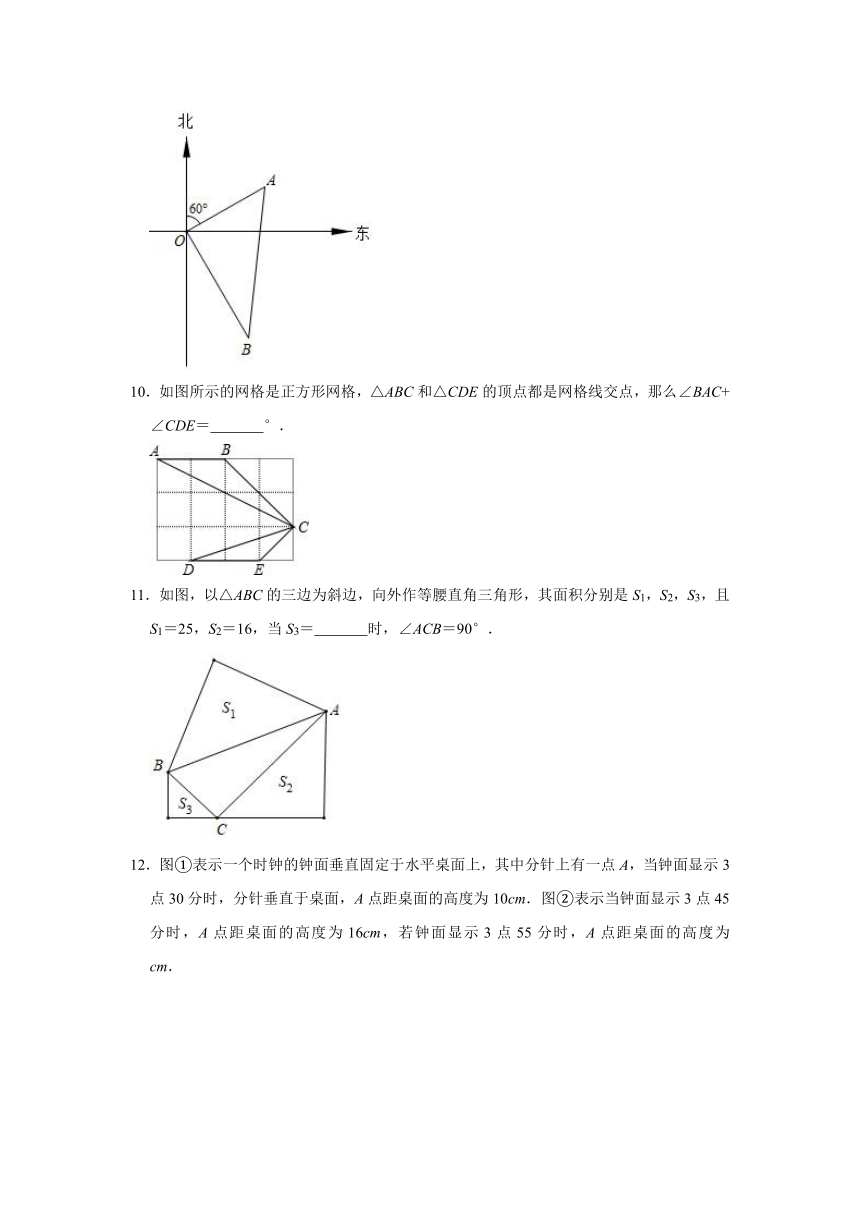
1.△ABC满足下列条件中的一个,其中不能说明△ABC是直角三角形的是( )
A.b2=(a+c)(a﹣c) B.a:b:c=1::2
C.∠C=∠A﹣∠B D.∠A:∠B:∠C=3:4:5
2.如图,在△ABC中,AB=8,BC=10,AC=6,则BC边上的高AD为( )
A.8 B.9 C. D.10
3.如图,一个梯子AB斜靠在一竖直的墙AO上,测得AO=4米,若梯子的顶端沿墙下滑1米,这时梯子的底端也恰好外移1米,则梯子AB的长度为( )
A.5米 B.6米 C.3米 D.7米
4.一个三角形的三边长分别为a2+b2,a2﹣b2,2ab,则这个三角形的形状为( )
A.钝角三角形 B.直角三角形
C.锐角三角形 D.形状不能确定
5.在平面直角坐标系中,点P(﹣x,2x)到原点O的距离等于5,则x的值是( )
A.±1 B.1 C. D.±
6.如图,高速公路上有A、B两点相距10km,C、D为两村庄,已知DA=4km,CB=6km.DA⊥AB于A,CB⊥AB于B,现要在AB上建一个服务站E,使得C、D两村庄到E站的距离相等,则EB的长是( )km
A.4 B.5 C.6 D.
7.如图,开口玻璃罐长、宽、高分别为16、6和6,在罐內点E处有一小块饼干碎末,此时一只蚂蚁正好在罐外长方形ABCD的中心H处,蚂蚁到达饼干的最短距离是多少( )
A. B. C. D.17
8.如果正整数a、b、c满足等式a2+b2=c2,那么正整数a、b、c叫做勾股数,某同学将自己探究勾股数的过程列成下表,观察表中每列数的规律,可知x+y的值为( )
A.47 B.62 C.79 D.98
二.填空题
9.如图,某港口P位于南北延伸的海岸线上,东面是大海远洋号,长峰号两艘轮船同时离开港P,各自沿固定方向航行,“远洋”号每小时航行12nmile,“长峰”号每小时航行16nmile,它们离开港口1小时后,分别到达A,B两个位置,且AB=20nmile,已知“远洋”号沿着北偏东60°方向航行,那么“长峰”号航行的方向是 .
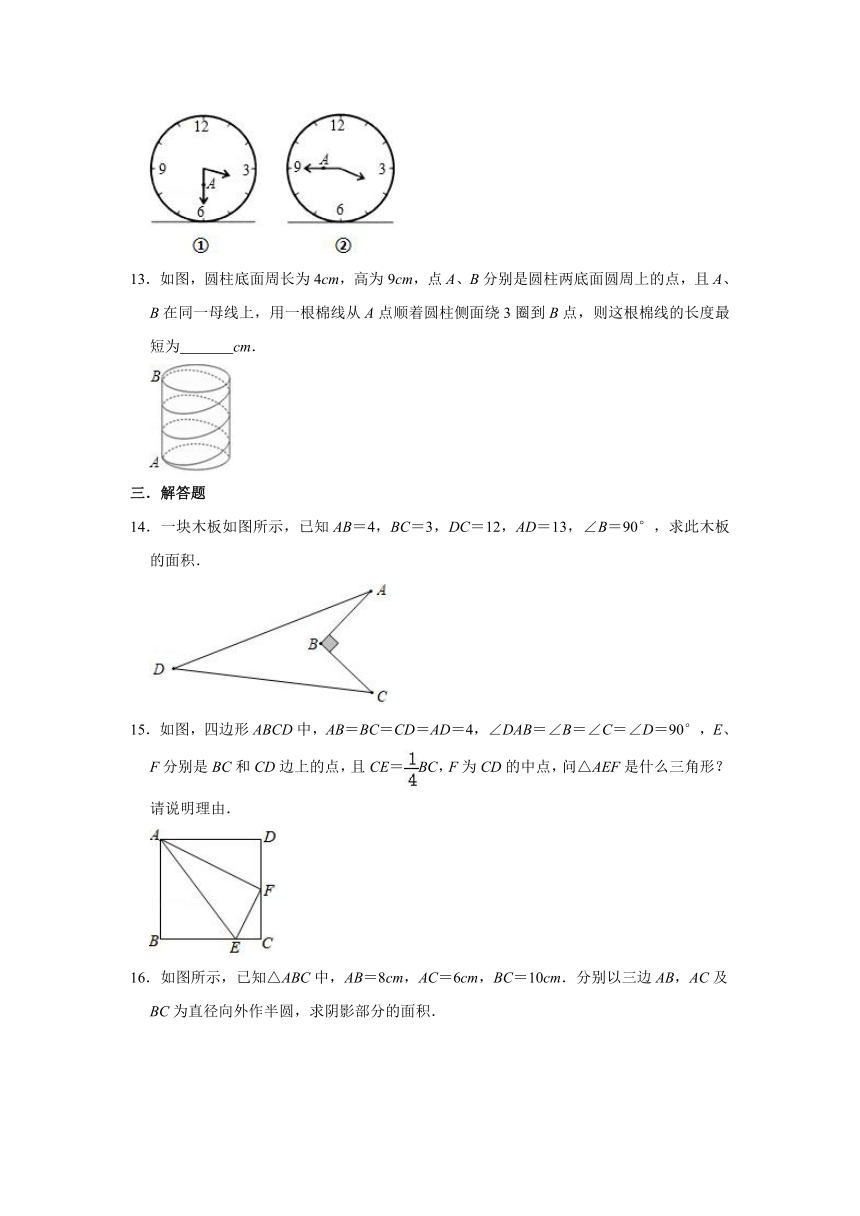
10.如图所示的网格是正方形网格,△ABC和△CDE的顶点都是网格线交点,那么∠BAC+∠CDE= °.
11.如图,以△ABC的三边为斜边,向外作等腰直角三角形,其面积分别是S1,S2,S3,且S1=25,S2=16,当S3= 时,∠ACB=90°.
12.图①表示一个时钟的钟面垂直固定于水平桌面上,其中分针上有一点A,当钟面显示3点30分时,分针垂直于桌面,A点距桌面的高度为10cm.图②表示当钟面显示3点45分时,A点距桌面的高度为16cm,若钟面显示3点55分时,A点距桌面的高度为 cm.
13.如图,圆柱底面周长为4cm,高为9cm,点A、B分别是圆柱两底面圆周上的点,且A、B在同一母线上,用一根棉线从A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为 cm.
三.解答题
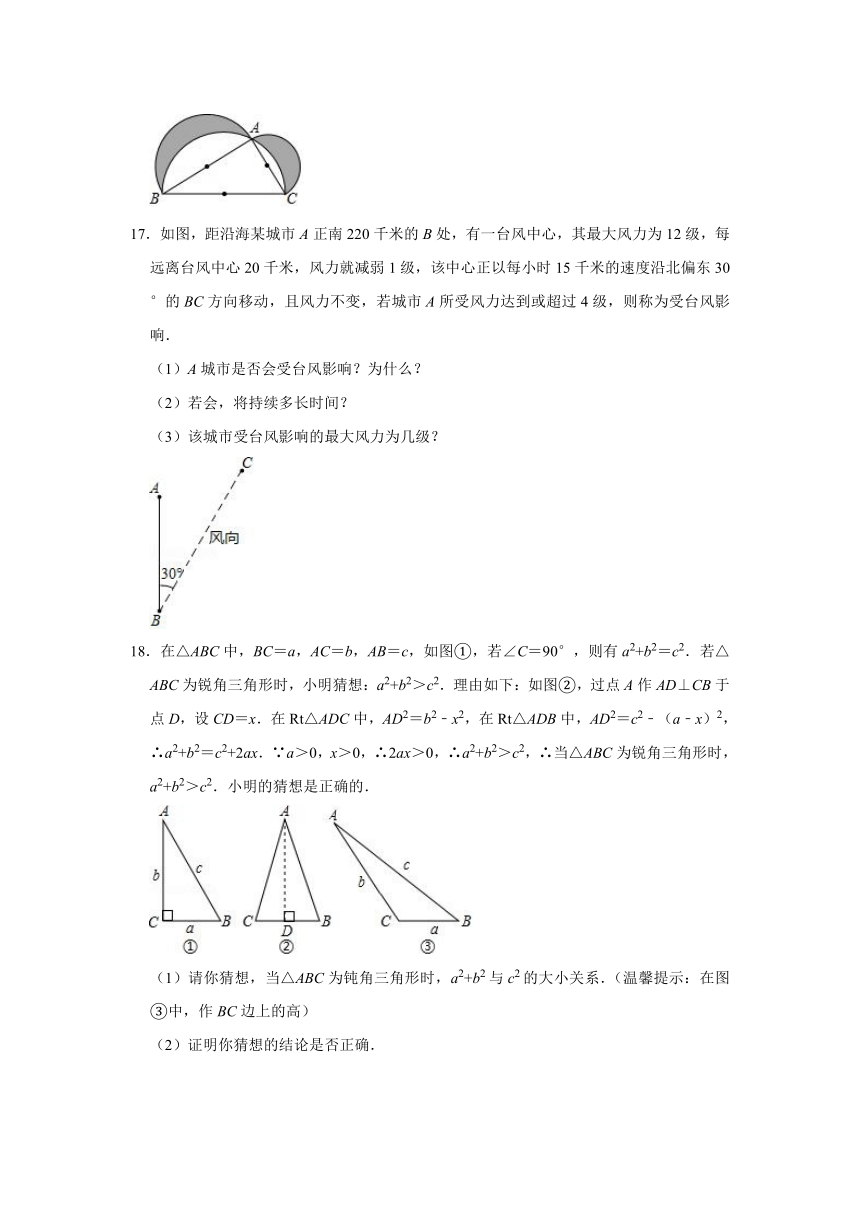
14.一块木板如图所示,已知AB=4,BC=3,DC=12,AD=13,∠B=90°,求此木板的面积.
15.如图,四边形ABCD中,AB=BC=CD=AD=4,∠DAB=∠B=∠C=∠D=90°,E、F分别是BC和CD边上的点,且CE=BC,F为CD的中点,问△AEF是什么三角形?请说明理由.
16.如图所示,已知△ABC中,AB=8cm,AC=6cm,BC=10cm.分别以三边AB,AC及BC为直径向外作半圆,求阴影部分的面积.
17.如图,距沿海某城市A正南220千米的B处,有一台风中心,其最大风力为12级,每远离台风中心20千米,风力就减弱1级,该中心正以每小时15千米的速度沿北偏东30°的BC方向移动,且风力不变,若城市A所受风力达到或超过4级,则称为受台风影响.
(1)A城市是否会受台风影响?为什么?
(2)若会,将持续多长时间?
(3)该城市受台风影响的最大风力为几级?
18.在△ABC中,BC=a,AC=b,AB=c,如图①,若∠C=90°,则有a2+b2=c2.若△ABC为锐角三角形时,小明猜想:a2+b2>c2.理由如下:如图②,过点A作AD⊥CB于点D,设CD=x.在Rt△ADC中,AD2=b2﹣x2,在Rt△ADB中,AD2=c2﹣(a﹣x)2,∴a2+b2=c2+2ax.∵a>0,x>0,∴2ax>0,∴a2+b2>c2,∴当△ABC为锐角三角形时,a2+b2>c2.小明的猜想是正确的.
(1)请你猜想,当△ABC为钝角三角形时,a2+b2与c2的大小关系.(温馨提示:在图③中,作BC边上的高)
(2)证明你猜想的结论是否正确.
参考答案
一.选择题
1.【解答】解:A、由b2=(a+c)(a﹣c)可得:c2+b2=a2,可以组成直角三角形,故此选项不符合题意;
B、12+()2=22,可以组成直角三角形,故此选项不符合题意;
C、由∠C=∠A﹣∠B,∠A+∠B+∠C=180°,可得:∠A=90°,可以组成直角三角形,故此选项不符合题意;
D、∵∠A:∠B:∠C=3:4:5,∠A+∠B+∠C=180°,∴最大角∠C=75°,∴不能构成直角三角形,故选项符合题意;
故选:D.
2.【解答】解:∵AB=8,BC=10,AC=6,
∴62+82=102,
∴△ABC是直角三角形,∠BAC=90°,
则由面积公式知,S△ABC=AB?AC=BC?AD,
∴AD=.
故选:C.
3.【解答】解:设BO=xm,依题意,得AC=1,BD=1,AO=4.
在Rt△AOB中,根据勾股定理得
AB2=AO2+OB2=42+x2,
在Rt△COD中,根据勾股定理
CD2=CO2+OD2=(4﹣1)2+(x+1)2,
∴42+x2=(4﹣1)2+(x+1)2,
解得x=3,
∴AB==5,
答:梯子AB的长为5m.
故选:A.
4.【解答】解:∵该三角形的三边长分别为a2+b2,a2﹣b2,2ab,且a2+b2>2ab,a2+b2>a2﹣b2,
∴(a2﹣b2)2+(2ab)2=a4﹣2a2b2+b4+4a2b2=(a2+b2)2,
∴该三角形是直角三角形.
故选:B.
5.【解答】解:∵点P(﹣x,2x)到原点O的距离等于5,
∴x2+4x2=25,解得x=±.
故选:D.
6.【解答】解:设BE=x,则AE=(10﹣x)km,
由勾股定理得:
在Rt△ADE中,
DE2=AD2+AE2=42+(10﹣x)2,
在Rt△BCE中,
CE2=BC2+BE2=62+x2,
由题意可知:DE=CE,
所以:62+x2=42+(10﹣x)2,
解得:x=4km.
所以,EB的长是4km.
故选:A.
7.【解答】解:①若蚂蚁从平面ABCD和平面CDFE经过,
蚂蚁到达饼干的最短距离如图1:
H′E==,
②若蚂蚁从平面ABCD和平面BCEH经过,
则蚂蚁到达饼干的最短距离如图2:
H′E==17,
故选:C.
8.【解答】解:由题可得,3=22﹣1,4=2×2,5=22+1,……
∴a=n2﹣1,b=2n,c=n2+1,
∴当c=n2+1=65时,n=8,
∴x=63,y=16,
∴x+y=79,
故选:C.
二.填空题
9.【解答】解:由题意得:P与O重合,如图所示:
OA=12nmile,OB=16nmile,AB=20nmile,
∵122+162=202,
∴OA2+OB2=AB2,
∴△PAB是直角三角形,
∴∠AOB=90°,
∵∠DOA=60°,
∴∠COP=180°﹣90°﹣60°=30°,
∴“长峰”号航行的方向是南偏东30°,
故答案为:南偏东30°.
10.【解答】解:连接AD,
由勾股定理得:AD2=12+32=10,CD2=12+32=10,AC2=22+42=20,
∴AD=CD,AD2+CD2=AC2,
∴∠ADC=90°,
∴∠DAC=∠ACD=45°,
∵AB∥DE,
∴∠BAD+∠ADE=180°,
∴∠BAC+∠CDE=180°﹣90°﹣45°=45°,
故答案为:45°.
11.【解答】解:当∠ACB=90°时,以△ABC的三边为斜边,向外作等腰直角三角形,
可得:S3+S2=S1,
∴S3=25﹣16=9,
故答案为:9
12.【解答】解:∵当钟面显示3点30分时,分针垂直于桌面,A点距桌面的高度为10cm.
∴AD=10,
∵钟面显示3点45分时,A点距桌面的高度为16cm,
∴A′C=16,
∴AO=A″O=6,
则钟面显示3点55分时,
∠A″OA′=30°,
∴FA″=3,
∴A点距桌面的高度为:16+3=19(cm).
故答案为:19.
13.【解答】解:圆柱体的展开图如图所示:用一棉线从A顺着圆柱侧面绕3圈到B的运动最短路线的长是:AC+EF+DB;
即在圆柱体的展开图长方形中,将长方形平均分成3个小长方形,A沿着3个长方形的对角线运动到B的路线最短;
∵长方形的宽即是圆柱体的底面周长是4cm;
又∵圆柱高为9cm,
∴小长方形的一条边长是3cm;
根据勾股定理求得AC=EF=DB=5cm;
∴AC+EF+DB=15cm;
故答案为:15.
三.解答题
14.【解答】解:连接AC,
∵在△ABC中,AB=4,BC=3,∠B=90°,
∴AC=5,
∵在△ACD中,AC=5,DC=12,AD=13,
∴DC2+AC2=122+52=169,AD2=132=169,
∴DC2+AC2=AD2,
∴△ACD为直角三角形,AD为斜边,
∴木板的面积为:S△ACD﹣S△ABC=×5×12﹣×3×4=24.
答:此木板的面积为24.
15.【解答】解:∵AB=BC=CD=AD=4,AB=4,CE=BC,
∴EC=1,BE=3,
∵F为CD的中点,
∴DF=FC=2,
∵∠DAB=∠B=∠C=∠D=90°,
∴EF==,
AF==,
AE==.
∴AE2=EF2+AF2.
∴△AEF是直角三角形.
16.【解答】解:∵82+62=102,
∴AB2+AC2=BC2
∴∠BAC=90°
∴以AB为直径的半圆的面积
以AC为直径的半圆的面积
以BC为直径的半圆的面积S3==π(cm2)
∴
17.【解答】解:(1)该城市会受到这次台风的影响.
理由是:如图,过A作AD⊥BC于D.在Rt△ABD中,
∵∠ABD=30°,AB=220,
∴,
∵城市受到的风力达到或超过四级,则称受台风影响,
∴受台风影响范围的半径为20×(12﹣4)=160.
∵110<160,
∴该城市会受到这次台风的影响.
(2)如图以A为圆心,160为半径作⊙A交BC于E、F.
则AE=AF=160.
∴台风影响该市持续的路程为:EF=2DE=2=60.
∴台风影响该市的持续时间t=60÷15=4(小时).
(3)∵AD距台风中心最近,
∴该城市受到这次台风最大风力为:12﹣(110÷20)=6.5(级).
18.【解答】解:(1)当△ABC为钝角三角形时,a2+b2与c2 的大小关系为:a2+b2<c2;
(2)如图③,过点A作AD⊥BC于点D,设CD=x,
在Rt△ADC中,AD2=b2﹣x2,
在Rt△ADB中,AD2=c2﹣(a+x)2,
∴b2﹣x2=c2﹣(a+x)2,
∴a2+b2=c2﹣2ax,
∵a>0,x>0,
∴2ax>0,
∴a2+b2<c2
即当△ABC为钝角三角形时,a2+b2<c2.
一.选择题
1.△ABC满足下列条件中的一个,其中不能说明△ABC是直角三角形的是( )
A.b2=(a+c)(a﹣c) B.a:b:c=1::2
C.∠C=∠A﹣∠B D.∠A:∠B:∠C=3:4:5
2.如图,在△ABC中,AB=8,BC=10,AC=6,则BC边上的高AD为( )
A.8 B.9 C. D.10
3.如图,一个梯子AB斜靠在一竖直的墙AO上,测得AO=4米,若梯子的顶端沿墙下滑1米,这时梯子的底端也恰好外移1米,则梯子AB的长度为( )
A.5米 B.6米 C.3米 D.7米
4.一个三角形的三边长分别为a2+b2,a2﹣b2,2ab,则这个三角形的形状为( )
A.钝角三角形 B.直角三角形
C.锐角三角形 D.形状不能确定
5.在平面直角坐标系中,点P(﹣x,2x)到原点O的距离等于5,则x的值是( )
A.±1 B.1 C. D.±
6.如图,高速公路上有A、B两点相距10km,C、D为两村庄,已知DA=4km,CB=6km.DA⊥AB于A,CB⊥AB于B,现要在AB上建一个服务站E,使得C、D两村庄到E站的距离相等,则EB的长是( )km
A.4 B.5 C.6 D.
7.如图,开口玻璃罐长、宽、高分别为16、6和6,在罐內点E处有一小块饼干碎末,此时一只蚂蚁正好在罐外长方形ABCD的中心H处,蚂蚁到达饼干的最短距离是多少( )
A. B. C. D.17
8.如果正整数a、b、c满足等式a2+b2=c2,那么正整数a、b、c叫做勾股数,某同学将自己探究勾股数的过程列成下表,观察表中每列数的规律,可知x+y的值为( )
A.47 B.62 C.79 D.98
二.填空题
9.如图,某港口P位于南北延伸的海岸线上,东面是大海远洋号,长峰号两艘轮船同时离开港P,各自沿固定方向航行,“远洋”号每小时航行12nmile,“长峰”号每小时航行16nmile,它们离开港口1小时后,分别到达A,B两个位置,且AB=20nmile,已知“远洋”号沿着北偏东60°方向航行,那么“长峰”号航行的方向是 .
10.如图所示的网格是正方形网格,△ABC和△CDE的顶点都是网格线交点,那么∠BAC+∠CDE= °.
11.如图,以△ABC的三边为斜边,向外作等腰直角三角形,其面积分别是S1,S2,S3,且S1=25,S2=16,当S3= 时,∠ACB=90°.
12.图①表示一个时钟的钟面垂直固定于水平桌面上,其中分针上有一点A,当钟面显示3点30分时,分针垂直于桌面,A点距桌面的高度为10cm.图②表示当钟面显示3点45分时,A点距桌面的高度为16cm,若钟面显示3点55分时,A点距桌面的高度为 cm.
13.如图,圆柱底面周长为4cm,高为9cm,点A、B分别是圆柱两底面圆周上的点,且A、B在同一母线上,用一根棉线从A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为 cm.
三.解答题
14.一块木板如图所示,已知AB=4,BC=3,DC=12,AD=13,∠B=90°,求此木板的面积.
15.如图,四边形ABCD中,AB=BC=CD=AD=4,∠DAB=∠B=∠C=∠D=90°,E、F分别是BC和CD边上的点,且CE=BC,F为CD的中点,问△AEF是什么三角形?请说明理由.
16.如图所示,已知△ABC中,AB=8cm,AC=6cm,BC=10cm.分别以三边AB,AC及BC为直径向外作半圆,求阴影部分的面积.
17.如图,距沿海某城市A正南220千米的B处,有一台风中心,其最大风力为12级,每远离台风中心20千米,风力就减弱1级,该中心正以每小时15千米的速度沿北偏东30°的BC方向移动,且风力不变,若城市A所受风力达到或超过4级,则称为受台风影响.
(1)A城市是否会受台风影响?为什么?
(2)若会,将持续多长时间?
(3)该城市受台风影响的最大风力为几级?
18.在△ABC中,BC=a,AC=b,AB=c,如图①,若∠C=90°,则有a2+b2=c2.若△ABC为锐角三角形时,小明猜想:a2+b2>c2.理由如下:如图②,过点A作AD⊥CB于点D,设CD=x.在Rt△ADC中,AD2=b2﹣x2,在Rt△ADB中,AD2=c2﹣(a﹣x)2,∴a2+b2=c2+2ax.∵a>0,x>0,∴2ax>0,∴a2+b2>c2,∴当△ABC为锐角三角形时,a2+b2>c2.小明的猜想是正确的.
(1)请你猜想,当△ABC为钝角三角形时,a2+b2与c2的大小关系.(温馨提示:在图③中,作BC边上的高)
(2)证明你猜想的结论是否正确.
参考答案
一.选择题
1.【解答】解:A、由b2=(a+c)(a﹣c)可得:c2+b2=a2,可以组成直角三角形,故此选项不符合题意;
B、12+()2=22,可以组成直角三角形,故此选项不符合题意;
C、由∠C=∠A﹣∠B,∠A+∠B+∠C=180°,可得:∠A=90°,可以组成直角三角形,故此选项不符合题意;
D、∵∠A:∠B:∠C=3:4:5,∠A+∠B+∠C=180°,∴最大角∠C=75°,∴不能构成直角三角形,故选项符合题意;
故选:D.
2.【解答】解:∵AB=8,BC=10,AC=6,
∴62+82=102,
∴△ABC是直角三角形,∠BAC=90°,
则由面积公式知,S△ABC=AB?AC=BC?AD,
∴AD=.
故选:C.
3.【解答】解:设BO=xm,依题意,得AC=1,BD=1,AO=4.
在Rt△AOB中,根据勾股定理得
AB2=AO2+OB2=42+x2,
在Rt△COD中,根据勾股定理
CD2=CO2+OD2=(4﹣1)2+(x+1)2,
∴42+x2=(4﹣1)2+(x+1)2,
解得x=3,
∴AB==5,
答:梯子AB的长为5m.
故选:A.
4.【解答】解:∵该三角形的三边长分别为a2+b2,a2﹣b2,2ab,且a2+b2>2ab,a2+b2>a2﹣b2,
∴(a2﹣b2)2+(2ab)2=a4﹣2a2b2+b4+4a2b2=(a2+b2)2,
∴该三角形是直角三角形.
故选:B.
5.【解答】解:∵点P(﹣x,2x)到原点O的距离等于5,
∴x2+4x2=25,解得x=±.
故选:D.
6.【解答】解:设BE=x,则AE=(10﹣x)km,
由勾股定理得:
在Rt△ADE中,
DE2=AD2+AE2=42+(10﹣x)2,
在Rt△BCE中,
CE2=BC2+BE2=62+x2,
由题意可知:DE=CE,
所以:62+x2=42+(10﹣x)2,
解得:x=4km.
所以,EB的长是4km.
故选:A.
7.【解答】解:①若蚂蚁从平面ABCD和平面CDFE经过,
蚂蚁到达饼干的最短距离如图1:
H′E==,
②若蚂蚁从平面ABCD和平面BCEH经过,
则蚂蚁到达饼干的最短距离如图2:
H′E==17,
故选:C.
8.【解答】解:由题可得,3=22﹣1,4=2×2,5=22+1,……
∴a=n2﹣1,b=2n,c=n2+1,
∴当c=n2+1=65时,n=8,
∴x=63,y=16,
∴x+y=79,
故选:C.
二.填空题
9.【解答】解:由题意得:P与O重合,如图所示:
OA=12nmile,OB=16nmile,AB=20nmile,
∵122+162=202,
∴OA2+OB2=AB2,
∴△PAB是直角三角形,
∴∠AOB=90°,
∵∠DOA=60°,
∴∠COP=180°﹣90°﹣60°=30°,
∴“长峰”号航行的方向是南偏东30°,
故答案为:南偏东30°.
10.【解答】解:连接AD,
由勾股定理得:AD2=12+32=10,CD2=12+32=10,AC2=22+42=20,
∴AD=CD,AD2+CD2=AC2,
∴∠ADC=90°,
∴∠DAC=∠ACD=45°,
∵AB∥DE,
∴∠BAD+∠ADE=180°,
∴∠BAC+∠CDE=180°﹣90°﹣45°=45°,
故答案为:45°.
11.【解答】解:当∠ACB=90°时,以△ABC的三边为斜边,向外作等腰直角三角形,
可得:S3+S2=S1,
∴S3=25﹣16=9,
故答案为:9
12.【解答】解:∵当钟面显示3点30分时,分针垂直于桌面,A点距桌面的高度为10cm.
∴AD=10,
∵钟面显示3点45分时,A点距桌面的高度为16cm,
∴A′C=16,
∴AO=A″O=6,
则钟面显示3点55分时,
∠A″OA′=30°,
∴FA″=3,
∴A点距桌面的高度为:16+3=19(cm).
故答案为:19.
13.【解答】解:圆柱体的展开图如图所示:用一棉线从A顺着圆柱侧面绕3圈到B的运动最短路线的长是:AC+EF+DB;
即在圆柱体的展开图长方形中,将长方形平均分成3个小长方形,A沿着3个长方形的对角线运动到B的路线最短;
∵长方形的宽即是圆柱体的底面周长是4cm;
又∵圆柱高为9cm,
∴小长方形的一条边长是3cm;
根据勾股定理求得AC=EF=DB=5cm;
∴AC+EF+DB=15cm;
故答案为:15.
三.解答题
14.【解答】解:连接AC,
∵在△ABC中,AB=4,BC=3,∠B=90°,
∴AC=5,
∵在△ACD中,AC=5,DC=12,AD=13,
∴DC2+AC2=122+52=169,AD2=132=169,
∴DC2+AC2=AD2,
∴△ACD为直角三角形,AD为斜边,
∴木板的面积为:S△ACD﹣S△ABC=×5×12﹣×3×4=24.
答:此木板的面积为24.
15.【解答】解:∵AB=BC=CD=AD=4,AB=4,CE=BC,
∴EC=1,BE=3,
∵F为CD的中点,
∴DF=FC=2,
∵∠DAB=∠B=∠C=∠D=90°,
∴EF==,
AF==,
AE==.
∴AE2=EF2+AF2.
∴△AEF是直角三角形.
16.【解答】解:∵82+62=102,
∴AB2+AC2=BC2
∴∠BAC=90°
∴以AB为直径的半圆的面积
以AC为直径的半圆的面积
以BC为直径的半圆的面积S3==π(cm2)
∴
17.【解答】解:(1)该城市会受到这次台风的影响.
理由是:如图,过A作AD⊥BC于D.在Rt△ABD中,
∵∠ABD=30°,AB=220,
∴,
∵城市受到的风力达到或超过四级,则称受台风影响,
∴受台风影响范围的半径为20×(12﹣4)=160.
∵110<160,
∴该城市会受到这次台风的影响.
(2)如图以A为圆心,160为半径作⊙A交BC于E、F.
则AE=AF=160.
∴台风影响该市持续的路程为:EF=2DE=2=60.
∴台风影响该市的持续时间t=60÷15=4(小时).
(3)∵AD距台风中心最近,
∴该城市受到这次台风最大风力为:12﹣(110÷20)=6.5(级).
18.【解答】解:(1)当△ABC为钝角三角形时,a2+b2与c2 的大小关系为:a2+b2<c2;
(2)如图③,过点A作AD⊥BC于点D,设CD=x,
在Rt△ADC中,AD2=b2﹣x2,
在Rt△ADB中,AD2=c2﹣(a+x)2,
∴b2﹣x2=c2﹣(a+x)2,
∴a2+b2=c2﹣2ax,
∵a>0,x>0,
∴2ax>0,
∴a2+b2<c2
即当△ABC为钝角三角形时,a2+b2<c2.
