第21章 二次函数与反比例函数 单元测试卷 2021-2022学年沪科版九年级数学上册(word版含解析)
文档属性
| 名称 | 第21章 二次函数与反比例函数 单元测试卷 2021-2022学年沪科版九年级数学上册(word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 237.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-29 09:03:51 | ||
图片预览


文档简介
第21章 二次函数与反比例函数
一、选择题(每小题5分,共50分)
1.点(﹣1,4)在反比例函数y=的图象上,则下列各点在此函数图象上的是( )
A.(4,﹣1) B.(﹣,1) C.(﹣4,﹣1) D.(,2)
2.如图,关于抛物线y=(x﹣1)2﹣2,下列说法错误的是( )
A.顶点坐标为(1,﹣2)
B.对称轴是直线x=l
C.开口方向向上
D.当x>1时,y随x的增大而减小
3.抛物线y=x2﹣6x+4的顶点坐标是( )
A.(3,5) B.(﹣3,5) C.(3,﹣5) D.(﹣3,﹣5)
4.如图,P(x,y)是反比例函数y=的图象在第一象限分支上的一个动点,PA⊥x轴于点A,PB⊥y轴于点B,随着自变量x的增大,矩形OAPB的面积( )
A.不变 B.增大 C.减小 D.无法确定
5.已知二次函数y=a(x+1)2﹣b(a≠0)有最小值1,则a,b的大小关系为( )
A.a>b B.a<b C.a=b D.不能确定
6.已知一次函数y=kx+b的图象经过一、二、四象限,则二次函数y=kx2+bx﹣k的顶点在第( )象限.
A.一 B.二 C.三 D.四
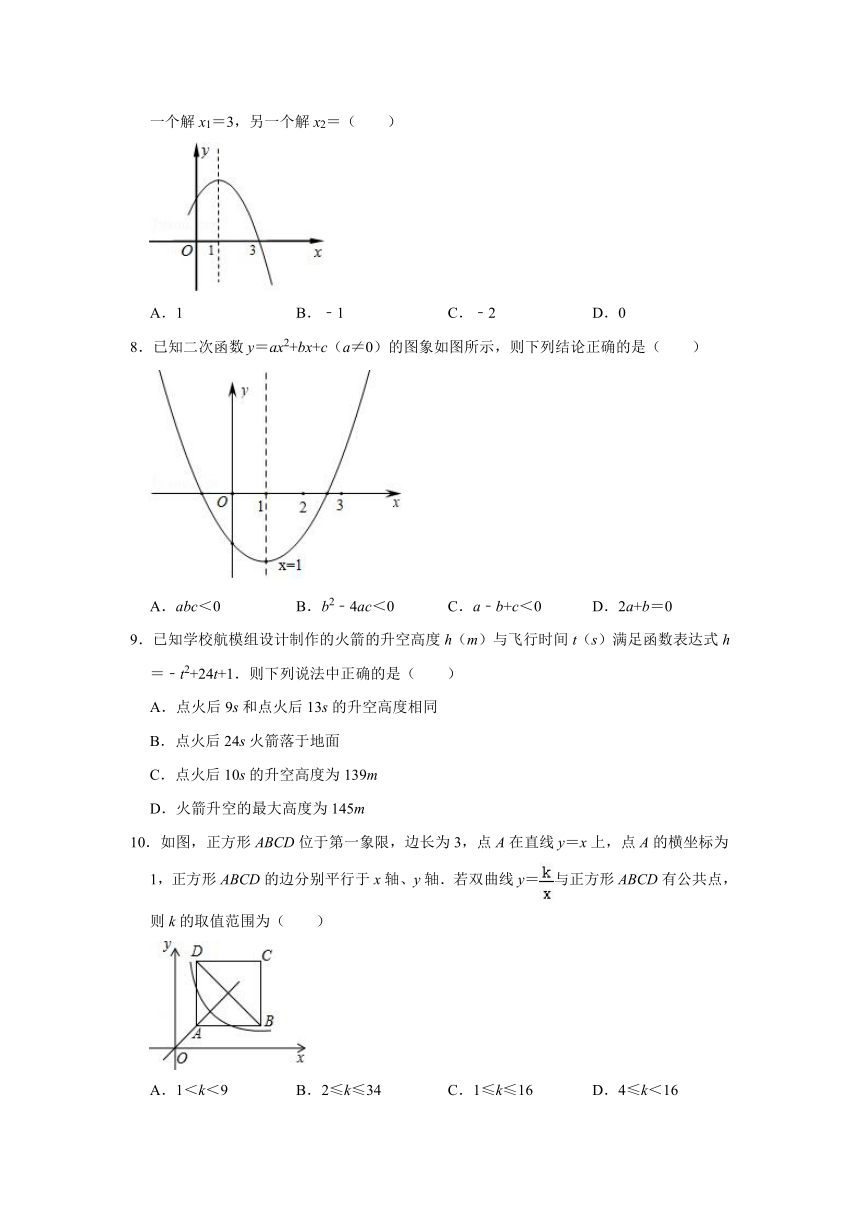
7.二次函数y=﹣x2+2x+k的部分图象如图所示,则关于x的一元二次方程﹣x2+2x+k=0的一个解x1=3,另一个解x2=( )
A.1 B.﹣1 C.﹣2 D.0
8.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论正确的是( )
A.abc<0 B.b2﹣4ac<0 C.a﹣b+c<0 D.2a+b=0
9.已知学校航模组设计制作的火箭的升空高度h(m)与飞行时间t(s)满足函数表达式h=﹣t2+24t+1.则下列说法中正确的是( )
A.点火后9s和点火后13s的升空高度相同
B.点火后24s火箭落于地面
C.点火后10s的升空高度为139m
D.火箭升空的最大高度为145m
10.如图,正方形ABCD位于第一象限,边长为3,点A在直线y=x上,点A的横坐标为1,正方形ABCD的边分别平行于x轴、y轴.若双曲线y=与正方形ABCD有公共点,则k的取值范围为( )
A.1<k<9 B.2≤k≤34 C.1≤k≤16 D.4≤k<16
二、填空题(每小题5分,共20分)
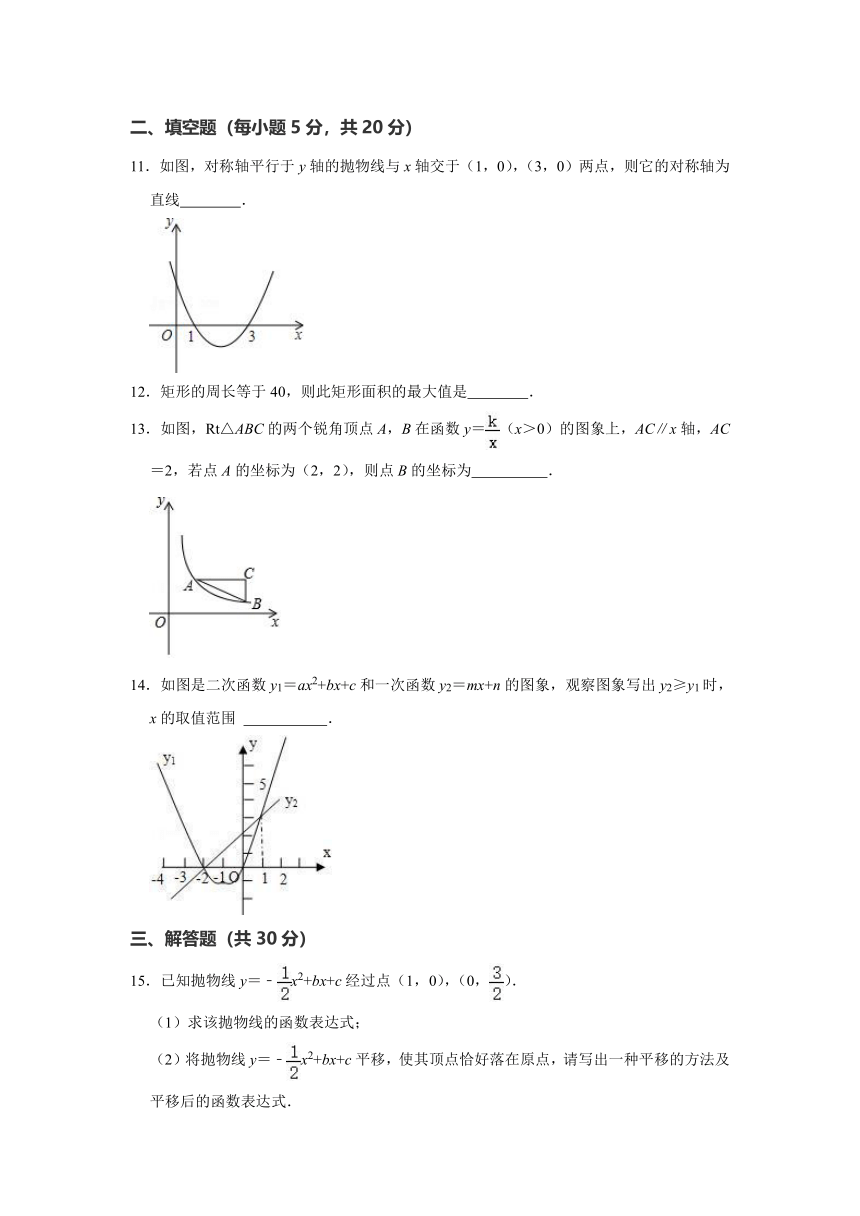
11.如图,对称轴平行于y轴的抛物线与x轴交于(1,0),(3,0)两点,则它的对称轴为直线 .
12.矩形的周长等于40,则此矩形面积的最大值是 .
13.如图,Rt△ABC的两个锐角顶点A,B在函数y=(x>0)的图象上,AC∥x轴,AC=2,若点A的坐标为(2,2),则点B的坐标为 .
14.如图是二次函数y1=ax2+bx+c和一次函数y2=mx+n的图象,观察图象写出y2≥y1时,x的取值范围 .
三、解答题(共30分)
15.已知抛物线y=﹣x2+bx+c经过点(1,0),(0,).
(1)求该抛物线的函数表达式;
(2)将抛物线y=﹣x2+bx+c平移,使其顶点恰好落在原点,请写出一种平移的方法及平移后的函数表达式.
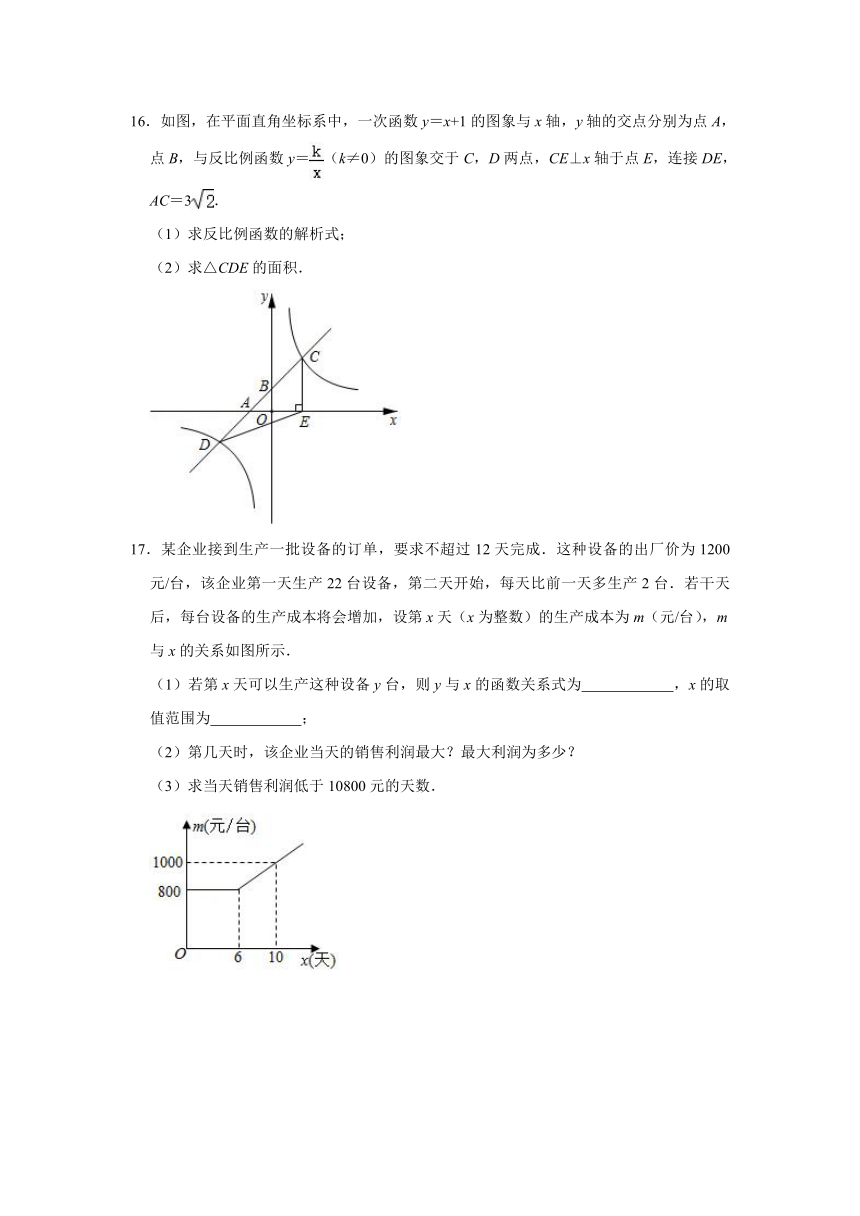
16.如图,在平面直角坐标系中,一次函数y=x+1的图象与x轴,y轴的交点分别为点A,点B,与反比例函数y=(k≠0)的图象交于C,D两点,CE⊥x轴于点E,连接DE,AC=3.
(1)求反比例函数的解析式;
(2)求△CDE的面积.
17.某企业接到生产一批设备的订单,要求不超过12天完成.这种设备的出厂价为1200元/台,该企业第一天生产22台设备,第二天开始,每天比前一天多生产2台.若干天后,每台设备的生产成本将会增加,设第x天(x为整数)的生产成本为m(元/台),m与x的关系如图所示.
(1)若第x天可以生产这种设备y台,则y与x的函数关系式为 ,x的取值范围为 ;
(2)第几天时,该企业当天的销售利润最大?最大利润为多少?
(3)求当天销售利润低于10800元的天数.
参考答案与试题解析
一.选择题(共10小题)
1.点(﹣1,4)在反比例函数y=的图象上,则下列各点在此函数图象上的是( )
A.(4,﹣1) B.(﹣,1) C.(﹣4,﹣1) D.(,2)
【分析】将点(﹣1,4)代入y=,求出函数解析式即可解题;
【解答】解:将点(﹣1,4)代入y=,
∴k=﹣4,
∴y=,
∴点(4,﹣1)在函数图象上,
故选:A.
2.如图,关于抛物线y=(x﹣1)2﹣2,下列说法错误的是( )
A.顶点坐标为(1,﹣2)
B.对称轴是直线x=l
C.开口方向向上
D.当x>1时,y随x的增大而减小
【分析】根据抛物线的解析式得出顶点坐标是(1,﹣2),对称轴是直线x=1,根据a=1>0,得出开口向上,当x>1时,y随x的增大而增大,根据结论即可判断选项.
【解答】解:∵抛物线y=(x﹣1)2﹣2,
A、因为顶点坐标是(1,﹣2),故说法正确;
B、因为对称轴是直线x=1,故说法正确;
C、因为a=1>0,开口向上,故说法正确;
D、当x>1时,y随x的增大而增大,故说法错误.
故选:D.
3.抛物线y=x2﹣6x+4的顶点坐标是( )
A.(3,5) B.(﹣3,5) C.(3,﹣5) D.(﹣3,﹣5)
【分析】直接利用配方法将二次函数写成顶点式进而得出其顶点坐标.
【解答】解:y=x2﹣6x+4=(x﹣3)2﹣5,
故抛物线y=x2﹣6x+4的顶点坐标是:(3,﹣5).
故选:C.
4.如图,P(x,y)是反比例函数y=的图象在第一象限分支上的一个动点,PA⊥x轴于点A,PB⊥y轴于点B,随着自变量x的增大,矩形OAPB的面积( )
A.不变 B.增大 C.减小 D.无法确定
【分析】因为过双曲线上任意一点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S是个定值,即S=|k|,所以随着x的逐渐增大,矩形OAPB的面积将不变.
【解答】解:依题意有矩形OAPB的面积=2×|k|=3,所以随着x的逐渐增大,矩形OAPB的面积将不变.
故选:A.
5.已知二次函数y=a(x+1)2﹣b(a≠0)有最小值1,则a,b的大小关系为( )
A.a>b B.a<b C.a=b D.不能确定
【分析】根据函数有最小值判断出a的符号,进而由最小值求出b,比较a、b可得出结论.
【解答】解:∵二次函数y=a(x+1)2﹣b(a≠0)有最小值,
∴抛物线开口方向向上,即a>0;
又∵最小值为1,即﹣b=1,∴b=﹣1,
∴a>b.
故选:A.
6.已知一次函数y=kx+b的图象经过一、二、四象限,则二次函数y=kx2+bx﹣k的顶点在第( )象限.
A.一 B.二 C.三 D.四
【分析】利用一次函数的性质得到k<0,b>0,则判断△>0得到抛物线与x轴有两个交点,然后确定抛物线的对称轴的位置,从而得到抛物线顶点所在的象限.
【解答】解:∵一次函数y=kx+b的图象经过一、二、四象限,
∴k<0,b>0,
∵△=b2﹣4k(﹣k)=b2+4k2>0,
∴抛物线与x轴有两个交点,
∵k、b异号,
∴抛物线的对称轴在y轴右侧,
∴二次函数y=kx2+bx﹣k的顶点在第一象限.
故选:A.
7.二次函数y=﹣x2+2x+k的部分图象如图所示,则关于x的一元二次方程﹣x2+2x+k=0的一个解x1=3,另一个解x2=( )
A.1 B.﹣1 C.﹣2 D.0
【分析】先把x1=3代入关于x的一元二次方程﹣x2+2x+k=0,求出k的值,再根据根与系数的关系即可求出另一个解x2的值.
【解答】解:∵把x1=3代入关于x的一元二次方程﹣x2+2x+k=0得,
﹣9+6+k=0,解得k=3,
∴原方程可化为:﹣x2+2x+3=0,
∴x1+x2=3+x2=﹣=2,解得x2=﹣1.
故选:B.
8.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论正确的是( )
A.abc<0 B.b2﹣4ac<0 C.a﹣b+c<0 D.2a+b=0
【分析】由图可知a>0,与y轴的交点c<0,对称轴x=1,函数与x轴有两个不同的交点,当x=﹣1时,y>0;
【解答】解:由图可知a>0,与y轴的交点c<0,对称轴x=1,
∴b=﹣2a<0;
∴abc>0,A错误;
由图象可知,函数与x轴有两个不同的交点,∴△>0,B错误;
当x=﹣1时,y>0,
∴a﹣b+c>0,C错误;
∵b=﹣2a,D正确;
故选:D.
9.已知学校航模组设计制作的火箭的升空高度h(m)与飞行时间t(s)满足函数表达式h=﹣t2+24t+1.则下列说法中正确的是( )
A.点火后9s和点火后13s的升空高度相同
B.点火后24s火箭落于地面
C.点火后10s的升空高度为139m
D.火箭升空的最大高度为145m
【分析】分别求出t=9、13、24、10时h的值可判断A、B、C三个选项,将解析式配方成顶点式可判断D选项.
【解答】解:A、当t=9时,h=136;当t=13时,h=144;所以点火后9s和点火后13s的升空高度不相同,此选项错误;
B、当t=24时h=1≠0,所以点火后24s火箭离地面的高度为1m,此选项错误;
C、当t=10时h=141m,此选项错误;
D、由h=﹣t2+24t+1=﹣(t﹣12)2+145知火箭升空的最大高度为145m,此选项正确;
故选:D.
10.如图,正方形ABCD位于第一象限,边长为3,点A在直线y=x上,点A的横坐标为1,正方形ABCD的边分别平行于x轴、y轴.若双曲线y=与正方形ABCD有公共点,则k的取值范围为( )
A.1<k<9 B.2≤k≤34 C.1≤k≤16 D.4≤k<16
【分析】先根据题意求出A点的坐标,再根据AB=BC=3,AB、BC分别平行于x轴、y轴求出B、C两点的坐标,再根据双曲线y=(k≠0)分别经过A、C两点时k的取值范围即可.
【解答】解:点A在直线y=x上,其中A点的横坐标为1,则把x=1代入y=x解得y=1,则A的坐标是(1,1),
∵AB=BC=3,
∴C点的坐标是(4,4),
∴当双曲线y=经过点(1,1)时,k=1;
当双曲线y=经过点(4,4)时,k=16,
因而1≤k≤16.
故选:C.
二.填空题(共4小题)
11.如图,对称轴平行于y轴的抛物线与x轴交于(1,0),(3,0)两点,则它的对称轴为直线 x=2 .
【分析】利用抛物线的对称性求解.
【解答】解:∵抛物线与x轴交于(1,0),(3,0)两点,
∴点(1,0)和点(3,0)为抛物线上的对称点,
∴点(1,0)与点(3,0)关于直线x=2对称,
∴抛物线的对称轴为直线x=2.
故答案为x=2.
12.矩形的周长等于40,则此矩形面积的最大值是 100 .
【分析】设矩形的宽为x,则长为(20﹣x),S=x(20﹣x)=﹣x2+20x=﹣(x﹣10)2+100,当x=10时,S最大值为100.
【解答】解:设矩形的宽为x,则长为(20﹣x),
S=x(20﹣x)=﹣x2+20x=﹣(x﹣10)2+100,
当x=10时,S最大值为100.
故答案为100.
13.如图,Rt△ABC的两个锐角顶点A,B在函数y=(x>0)的图象上,AC∥x轴,AC=2,若点A的坐标为(2,2),则点B的坐标为 (4,1) .
【分析】根据点A的坐标可以求得反比例函数的解析式和点B的横坐标,进而求得点B的坐标,本题得以解决.
【解答】解:∵点A(2,2)在函数y=(x>0)的图象上,
∴2=,得k=4,
∵在Rt△ABC中,AC∥x轴,AC=2,
∴点B的横坐标是4,
∴y==1,
∴点B的坐标为(4,1),
故答案为:(4,1).
14.如图是二次函数y1=ax2+bx+c和一次函数y2=mx+n的图象,观察图象写出y2≥y1时,x的取值范围 ﹣2≤x≤1 .
【分析】观察图象可知,y1与y2的两交点横坐标为﹣2,1;当y2≥y1时,就是两图象交点之间的部分,可求此时x的取值范围.
【解答】解:∵y1与y2的两交点横坐标为﹣2,1,
当y2≥y1时,y2的图象应在y1的图象上面,
即两图象交点之间的部分,
∴此时x的取值范围是﹣2≤x≤1.
三.解答题(共3小题)
15.已知抛物线y=﹣x2+bx+c经过点(1,0),(0,).
(1)求该抛物线的函数表达式;
(2)将抛物线y=﹣x2+bx+c平移,使其顶点恰好落在原点,请写出一种平移的方法及平移后的函数表达式.
【分析】(1)把已知点的坐标代入抛物线解析式求出b与c的值即可;
(2)指出满足题意的平移方法,并写出平移后的解析式即可.
【解答】解:(1)把(1,0),(0,)代入抛物线解析式得:,
解得:,
则抛物线解析式为y=﹣x2﹣x+;
(2)抛物线解析式为y=﹣x2﹣x+=﹣(x+1)2+2,
将抛物线向右平移一个单位,向下平移2个单位,解析式变为y=﹣x2.
16.如图,在平面直角坐标系中,一次函数y=x+1的图象与x轴,y轴的交点分别为点A,点B,与反比例函数y=(k≠0)的图象交于C,D两点,CE⊥x轴于点E,连接DE,AC=3.
(1)求反比例函数的解析式;
(2)求△CDE的面积.
【分析】(1)根据一次函数表达式推出△CAE为等腰直角三角形,得到AE=CE,再由AC的长求出AE和CE,再求出点A坐标,得到OE的长,从而得到点C坐标,即可求出k值;
(2)联立一次函数和反比例函数表达式,求出交点D的坐标,再用乘以CE乘以C、D两点横坐标之差求出△CDE的面积.
【解答】解:(1)∵一次函数y=x+1与x轴和y轴分别交于点A和点B,
∴∠CAE=45°,即△CAE为等腰直角三角形,
∴AE=CE,
∵AC=,即,
解得:AE=CE=3,
在y=x+1中,令y=0,则x=﹣1,
∴A(﹣1,0),
令y=3,得到x=2,
∴OE=2,CE=3,
∴C(2,3),
∴k=2×3=6,
∴反比例函数表达式为:,
(2)联立:,
解得:x=2或﹣3,
当x=﹣3时,y=﹣2,
∴点D的坐标为(﹣3,﹣2),
∴S△CDE=×3×[2﹣(﹣3)]=.
17.某企业接到生产一批设备的订单,要求不超过12天完成.这种设备的出厂价为1200元/台,该企业第一天生产22台设备,第二天开始,每天比前一天多生产2台.若干天后,每台设备的生产成本将会增加,设第x天(x为整数)的生产成本为m(元/台),m与x的关系如图所示.
(1)若第x天可以生产这种设备y台,则y与x的函数关系式为 y=2x+20 ,x的取值范围为 1≤x≤12 ;
(2)第几天时,该企业当天的销售利润最大?最大利润为多少?
(3)求当天销售利润低于10800元的天数.
【分析】(1)根据题意确定一次函数的解析式,实际问题中x的取值范围要使实际问题有意义;
(2)求出当天利润与天数的函数解析式,确定其最大值即可;
(3)根据(2)中的函数解析式列出不等式即可解答.
【解答】解:(1)根据题意,得y与x的解析式为:y=22+2(x﹣1)=2x+20(1≤x≤12),
故答案为:y=2x+20,1≤x≤12;
(2)设当天的销售利润为w元,
则当1≤x≤6时,
w=(1200﹣800)(2x+20)=800x+8000,
∵800>0,
∴w随x的增大而增大,
∴当x=6时,w最大值=800×6+8000=12800.
当6<x≤12时,
设m=kx+b,将(6,800)和(10,1000)代入得:
,
解得:,
∴m与x的关系式为:m=50x+500,
∴w=[1200﹣(50x+500)]×(2x+20)
=﹣100x2+400x+14000
=﹣100(x﹣2)2+14400.
∵此时图象开口向下,在对称轴右侧,w随x的增大而减小,天数x为整数,
∴当x=7时,w有最大值,为11900元,
∵12800>11900,
∴当x=6时,w最大,且w最大值=12800元,
答:该厂第6天获得的利润最大,最大利润是12800元.
(3)由(2)可得,
1≤x≤6时,800x+8000<10800,
解得:x<3.5
则第1﹣3天当天利润低于10800元,
当6<x≤12时,﹣100(x﹣2)2+14400<10800,
解得x<﹣4(舍去),或x>8,
∴第9﹣12天当天利润低于10800元,
故当天销售利润低于10800元的天数有7天.
一、选择题(每小题5分,共50分)
1.点(﹣1,4)在反比例函数y=的图象上,则下列各点在此函数图象上的是( )
A.(4,﹣1) B.(﹣,1) C.(﹣4,﹣1) D.(,2)
2.如图,关于抛物线y=(x﹣1)2﹣2,下列说法错误的是( )
A.顶点坐标为(1,﹣2)
B.对称轴是直线x=l
C.开口方向向上
D.当x>1时,y随x的增大而减小
3.抛物线y=x2﹣6x+4的顶点坐标是( )
A.(3,5) B.(﹣3,5) C.(3,﹣5) D.(﹣3,﹣5)
4.如图,P(x,y)是反比例函数y=的图象在第一象限分支上的一个动点,PA⊥x轴于点A,PB⊥y轴于点B,随着自变量x的增大,矩形OAPB的面积( )
A.不变 B.增大 C.减小 D.无法确定
5.已知二次函数y=a(x+1)2﹣b(a≠0)有最小值1,则a,b的大小关系为( )
A.a>b B.a<b C.a=b D.不能确定
6.已知一次函数y=kx+b的图象经过一、二、四象限,则二次函数y=kx2+bx﹣k的顶点在第( )象限.
A.一 B.二 C.三 D.四
7.二次函数y=﹣x2+2x+k的部分图象如图所示,则关于x的一元二次方程﹣x2+2x+k=0的一个解x1=3,另一个解x2=( )
A.1 B.﹣1 C.﹣2 D.0
8.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论正确的是( )
A.abc<0 B.b2﹣4ac<0 C.a﹣b+c<0 D.2a+b=0
9.已知学校航模组设计制作的火箭的升空高度h(m)与飞行时间t(s)满足函数表达式h=﹣t2+24t+1.则下列说法中正确的是( )
A.点火后9s和点火后13s的升空高度相同
B.点火后24s火箭落于地面
C.点火后10s的升空高度为139m
D.火箭升空的最大高度为145m
10.如图,正方形ABCD位于第一象限,边长为3,点A在直线y=x上,点A的横坐标为1,正方形ABCD的边分别平行于x轴、y轴.若双曲线y=与正方形ABCD有公共点,则k的取值范围为( )
A.1<k<9 B.2≤k≤34 C.1≤k≤16 D.4≤k<16
二、填空题(每小题5分,共20分)
11.如图,对称轴平行于y轴的抛物线与x轴交于(1,0),(3,0)两点,则它的对称轴为直线 .
12.矩形的周长等于40,则此矩形面积的最大值是 .
13.如图,Rt△ABC的两个锐角顶点A,B在函数y=(x>0)的图象上,AC∥x轴,AC=2,若点A的坐标为(2,2),则点B的坐标为 .
14.如图是二次函数y1=ax2+bx+c和一次函数y2=mx+n的图象,观察图象写出y2≥y1时,x的取值范围 .
三、解答题(共30分)
15.已知抛物线y=﹣x2+bx+c经过点(1,0),(0,).
(1)求该抛物线的函数表达式;
(2)将抛物线y=﹣x2+bx+c平移,使其顶点恰好落在原点,请写出一种平移的方法及平移后的函数表达式.
16.如图,在平面直角坐标系中,一次函数y=x+1的图象与x轴,y轴的交点分别为点A,点B,与反比例函数y=(k≠0)的图象交于C,D两点,CE⊥x轴于点E,连接DE,AC=3.
(1)求反比例函数的解析式;
(2)求△CDE的面积.
17.某企业接到生产一批设备的订单,要求不超过12天完成.这种设备的出厂价为1200元/台,该企业第一天生产22台设备,第二天开始,每天比前一天多生产2台.若干天后,每台设备的生产成本将会增加,设第x天(x为整数)的生产成本为m(元/台),m与x的关系如图所示.
(1)若第x天可以生产这种设备y台,则y与x的函数关系式为 ,x的取值范围为 ;
(2)第几天时,该企业当天的销售利润最大?最大利润为多少?
(3)求当天销售利润低于10800元的天数.
参考答案与试题解析
一.选择题(共10小题)
1.点(﹣1,4)在反比例函数y=的图象上,则下列各点在此函数图象上的是( )
A.(4,﹣1) B.(﹣,1) C.(﹣4,﹣1) D.(,2)
【分析】将点(﹣1,4)代入y=,求出函数解析式即可解题;
【解答】解:将点(﹣1,4)代入y=,
∴k=﹣4,
∴y=,
∴点(4,﹣1)在函数图象上,
故选:A.
2.如图,关于抛物线y=(x﹣1)2﹣2,下列说法错误的是( )
A.顶点坐标为(1,﹣2)
B.对称轴是直线x=l
C.开口方向向上
D.当x>1时,y随x的增大而减小
【分析】根据抛物线的解析式得出顶点坐标是(1,﹣2),对称轴是直线x=1,根据a=1>0,得出开口向上,当x>1时,y随x的增大而增大,根据结论即可判断选项.
【解答】解:∵抛物线y=(x﹣1)2﹣2,
A、因为顶点坐标是(1,﹣2),故说法正确;
B、因为对称轴是直线x=1,故说法正确;
C、因为a=1>0,开口向上,故说法正确;
D、当x>1时,y随x的增大而增大,故说法错误.
故选:D.
3.抛物线y=x2﹣6x+4的顶点坐标是( )
A.(3,5) B.(﹣3,5) C.(3,﹣5) D.(﹣3,﹣5)
【分析】直接利用配方法将二次函数写成顶点式进而得出其顶点坐标.
【解答】解:y=x2﹣6x+4=(x﹣3)2﹣5,
故抛物线y=x2﹣6x+4的顶点坐标是:(3,﹣5).
故选:C.
4.如图,P(x,y)是反比例函数y=的图象在第一象限分支上的一个动点,PA⊥x轴于点A,PB⊥y轴于点B,随着自变量x的增大,矩形OAPB的面积( )
A.不变 B.增大 C.减小 D.无法确定
【分析】因为过双曲线上任意一点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S是个定值,即S=|k|,所以随着x的逐渐增大,矩形OAPB的面积将不变.
【解答】解:依题意有矩形OAPB的面积=2×|k|=3,所以随着x的逐渐增大,矩形OAPB的面积将不变.
故选:A.
5.已知二次函数y=a(x+1)2﹣b(a≠0)有最小值1,则a,b的大小关系为( )
A.a>b B.a<b C.a=b D.不能确定
【分析】根据函数有最小值判断出a的符号,进而由最小值求出b,比较a、b可得出结论.
【解答】解:∵二次函数y=a(x+1)2﹣b(a≠0)有最小值,
∴抛物线开口方向向上,即a>0;
又∵最小值为1,即﹣b=1,∴b=﹣1,
∴a>b.
故选:A.
6.已知一次函数y=kx+b的图象经过一、二、四象限,则二次函数y=kx2+bx﹣k的顶点在第( )象限.
A.一 B.二 C.三 D.四
【分析】利用一次函数的性质得到k<0,b>0,则判断△>0得到抛物线与x轴有两个交点,然后确定抛物线的对称轴的位置,从而得到抛物线顶点所在的象限.
【解答】解:∵一次函数y=kx+b的图象经过一、二、四象限,
∴k<0,b>0,
∵△=b2﹣4k(﹣k)=b2+4k2>0,
∴抛物线与x轴有两个交点,
∵k、b异号,
∴抛物线的对称轴在y轴右侧,
∴二次函数y=kx2+bx﹣k的顶点在第一象限.
故选:A.
7.二次函数y=﹣x2+2x+k的部分图象如图所示,则关于x的一元二次方程﹣x2+2x+k=0的一个解x1=3,另一个解x2=( )
A.1 B.﹣1 C.﹣2 D.0
【分析】先把x1=3代入关于x的一元二次方程﹣x2+2x+k=0,求出k的值,再根据根与系数的关系即可求出另一个解x2的值.
【解答】解:∵把x1=3代入关于x的一元二次方程﹣x2+2x+k=0得,
﹣9+6+k=0,解得k=3,
∴原方程可化为:﹣x2+2x+3=0,
∴x1+x2=3+x2=﹣=2,解得x2=﹣1.
故选:B.
8.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论正确的是( )
A.abc<0 B.b2﹣4ac<0 C.a﹣b+c<0 D.2a+b=0
【分析】由图可知a>0,与y轴的交点c<0,对称轴x=1,函数与x轴有两个不同的交点,当x=﹣1时,y>0;
【解答】解:由图可知a>0,与y轴的交点c<0,对称轴x=1,
∴b=﹣2a<0;
∴abc>0,A错误;
由图象可知,函数与x轴有两个不同的交点,∴△>0,B错误;
当x=﹣1时,y>0,
∴a﹣b+c>0,C错误;
∵b=﹣2a,D正确;
故选:D.
9.已知学校航模组设计制作的火箭的升空高度h(m)与飞行时间t(s)满足函数表达式h=﹣t2+24t+1.则下列说法中正确的是( )
A.点火后9s和点火后13s的升空高度相同
B.点火后24s火箭落于地面
C.点火后10s的升空高度为139m
D.火箭升空的最大高度为145m
【分析】分别求出t=9、13、24、10时h的值可判断A、B、C三个选项,将解析式配方成顶点式可判断D选项.
【解答】解:A、当t=9时,h=136;当t=13时,h=144;所以点火后9s和点火后13s的升空高度不相同,此选项错误;
B、当t=24时h=1≠0,所以点火后24s火箭离地面的高度为1m,此选项错误;
C、当t=10时h=141m,此选项错误;
D、由h=﹣t2+24t+1=﹣(t﹣12)2+145知火箭升空的最大高度为145m,此选项正确;
故选:D.
10.如图,正方形ABCD位于第一象限,边长为3,点A在直线y=x上,点A的横坐标为1,正方形ABCD的边分别平行于x轴、y轴.若双曲线y=与正方形ABCD有公共点,则k的取值范围为( )
A.1<k<9 B.2≤k≤34 C.1≤k≤16 D.4≤k<16
【分析】先根据题意求出A点的坐标,再根据AB=BC=3,AB、BC分别平行于x轴、y轴求出B、C两点的坐标,再根据双曲线y=(k≠0)分别经过A、C两点时k的取值范围即可.
【解答】解:点A在直线y=x上,其中A点的横坐标为1,则把x=1代入y=x解得y=1,则A的坐标是(1,1),
∵AB=BC=3,
∴C点的坐标是(4,4),
∴当双曲线y=经过点(1,1)时,k=1;
当双曲线y=经过点(4,4)时,k=16,
因而1≤k≤16.
故选:C.
二.填空题(共4小题)
11.如图,对称轴平行于y轴的抛物线与x轴交于(1,0),(3,0)两点,则它的对称轴为直线 x=2 .
【分析】利用抛物线的对称性求解.
【解答】解:∵抛物线与x轴交于(1,0),(3,0)两点,
∴点(1,0)和点(3,0)为抛物线上的对称点,
∴点(1,0)与点(3,0)关于直线x=2对称,
∴抛物线的对称轴为直线x=2.
故答案为x=2.
12.矩形的周长等于40,则此矩形面积的最大值是 100 .
【分析】设矩形的宽为x,则长为(20﹣x),S=x(20﹣x)=﹣x2+20x=﹣(x﹣10)2+100,当x=10时,S最大值为100.
【解答】解:设矩形的宽为x,则长为(20﹣x),
S=x(20﹣x)=﹣x2+20x=﹣(x﹣10)2+100,
当x=10时,S最大值为100.
故答案为100.
13.如图,Rt△ABC的两个锐角顶点A,B在函数y=(x>0)的图象上,AC∥x轴,AC=2,若点A的坐标为(2,2),则点B的坐标为 (4,1) .
【分析】根据点A的坐标可以求得反比例函数的解析式和点B的横坐标,进而求得点B的坐标,本题得以解决.
【解答】解:∵点A(2,2)在函数y=(x>0)的图象上,
∴2=,得k=4,
∵在Rt△ABC中,AC∥x轴,AC=2,
∴点B的横坐标是4,
∴y==1,
∴点B的坐标为(4,1),
故答案为:(4,1).
14.如图是二次函数y1=ax2+bx+c和一次函数y2=mx+n的图象,观察图象写出y2≥y1时,x的取值范围 ﹣2≤x≤1 .
【分析】观察图象可知,y1与y2的两交点横坐标为﹣2,1;当y2≥y1时,就是两图象交点之间的部分,可求此时x的取值范围.
【解答】解:∵y1与y2的两交点横坐标为﹣2,1,
当y2≥y1时,y2的图象应在y1的图象上面,
即两图象交点之间的部分,
∴此时x的取值范围是﹣2≤x≤1.
三.解答题(共3小题)
15.已知抛物线y=﹣x2+bx+c经过点(1,0),(0,).
(1)求该抛物线的函数表达式;
(2)将抛物线y=﹣x2+bx+c平移,使其顶点恰好落在原点,请写出一种平移的方法及平移后的函数表达式.
【分析】(1)把已知点的坐标代入抛物线解析式求出b与c的值即可;
(2)指出满足题意的平移方法,并写出平移后的解析式即可.
【解答】解:(1)把(1,0),(0,)代入抛物线解析式得:,
解得:,
则抛物线解析式为y=﹣x2﹣x+;
(2)抛物线解析式为y=﹣x2﹣x+=﹣(x+1)2+2,
将抛物线向右平移一个单位,向下平移2个单位,解析式变为y=﹣x2.
16.如图,在平面直角坐标系中,一次函数y=x+1的图象与x轴,y轴的交点分别为点A,点B,与反比例函数y=(k≠0)的图象交于C,D两点,CE⊥x轴于点E,连接DE,AC=3.
(1)求反比例函数的解析式;
(2)求△CDE的面积.
【分析】(1)根据一次函数表达式推出△CAE为等腰直角三角形,得到AE=CE,再由AC的长求出AE和CE,再求出点A坐标,得到OE的长,从而得到点C坐标,即可求出k值;
(2)联立一次函数和反比例函数表达式,求出交点D的坐标,再用乘以CE乘以C、D两点横坐标之差求出△CDE的面积.
【解答】解:(1)∵一次函数y=x+1与x轴和y轴分别交于点A和点B,
∴∠CAE=45°,即△CAE为等腰直角三角形,
∴AE=CE,
∵AC=,即,
解得:AE=CE=3,
在y=x+1中,令y=0,则x=﹣1,
∴A(﹣1,0),
令y=3,得到x=2,
∴OE=2,CE=3,
∴C(2,3),
∴k=2×3=6,
∴反比例函数表达式为:,
(2)联立:,
解得:x=2或﹣3,
当x=﹣3时,y=﹣2,
∴点D的坐标为(﹣3,﹣2),
∴S△CDE=×3×[2﹣(﹣3)]=.
17.某企业接到生产一批设备的订单,要求不超过12天完成.这种设备的出厂价为1200元/台,该企业第一天生产22台设备,第二天开始,每天比前一天多生产2台.若干天后,每台设备的生产成本将会增加,设第x天(x为整数)的生产成本为m(元/台),m与x的关系如图所示.
(1)若第x天可以生产这种设备y台,则y与x的函数关系式为 y=2x+20 ,x的取值范围为 1≤x≤12 ;
(2)第几天时,该企业当天的销售利润最大?最大利润为多少?
(3)求当天销售利润低于10800元的天数.
【分析】(1)根据题意确定一次函数的解析式,实际问题中x的取值范围要使实际问题有意义;
(2)求出当天利润与天数的函数解析式,确定其最大值即可;
(3)根据(2)中的函数解析式列出不等式即可解答.
【解答】解:(1)根据题意,得y与x的解析式为:y=22+2(x﹣1)=2x+20(1≤x≤12),
故答案为:y=2x+20,1≤x≤12;
(2)设当天的销售利润为w元,
则当1≤x≤6时,
w=(1200﹣800)(2x+20)=800x+8000,
∵800>0,
∴w随x的增大而增大,
∴当x=6时,w最大值=800×6+8000=12800.
当6<x≤12时,
设m=kx+b,将(6,800)和(10,1000)代入得:
,
解得:,
∴m与x的关系式为:m=50x+500,
∴w=[1200﹣(50x+500)]×(2x+20)
=﹣100x2+400x+14000
=﹣100(x﹣2)2+14400.
∵此时图象开口向下,在对称轴右侧,w随x的增大而减小,天数x为整数,
∴当x=7时,w有最大值,为11900元,
∵12800>11900,
∴当x=6时,w最大,且w最大值=12800元,
答:该厂第6天获得的利润最大,最大利润是12800元.
(3)由(2)可得,
1≤x≤6时,800x+8000<10800,
解得:x<3.5
则第1﹣3天当天利润低于10800元,
当6<x≤12时,﹣100(x﹣2)2+14400<10800,
解得x<﹣4(舍去),或x>8,
∴第9﹣12天当天利润低于10800元,
故当天销售利润低于10800元的天数有7天.
