12.3 一次函数与二元一次方程练习题 2021——2022学年沪科版八年级数学上册(2课时 Word版 含答案)
文档属性
| 名称 | 12.3 一次函数与二元一次方程练习题 2021——2022学年沪科版八年级数学上册(2课时 Word版 含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 313.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-30 00:00:00 | ||
图片预览




文档简介
12.3 一次函数与二元一次方程
第1课时 一次函数与二元一次方程的关系
【基础练习】
知识点 二元一次方程与一次函数的关系
1.二元一次方程3x-2y=12有无数组解,在求方程的解时,用一个未知数x表示y为 ,给出x的一个值,计算出对应的y值.这个过程与描点法画函数图象时的列表是一致的,因此以方程3x-2y=12的解为坐标的点,都在一次函数 的图象上.?
2.根据画函数图象的过程可知,一次函数y=kx+b(k,b为常数,且k≠0)图象上点的坐标对应的一对实数,都是方程 的解.?
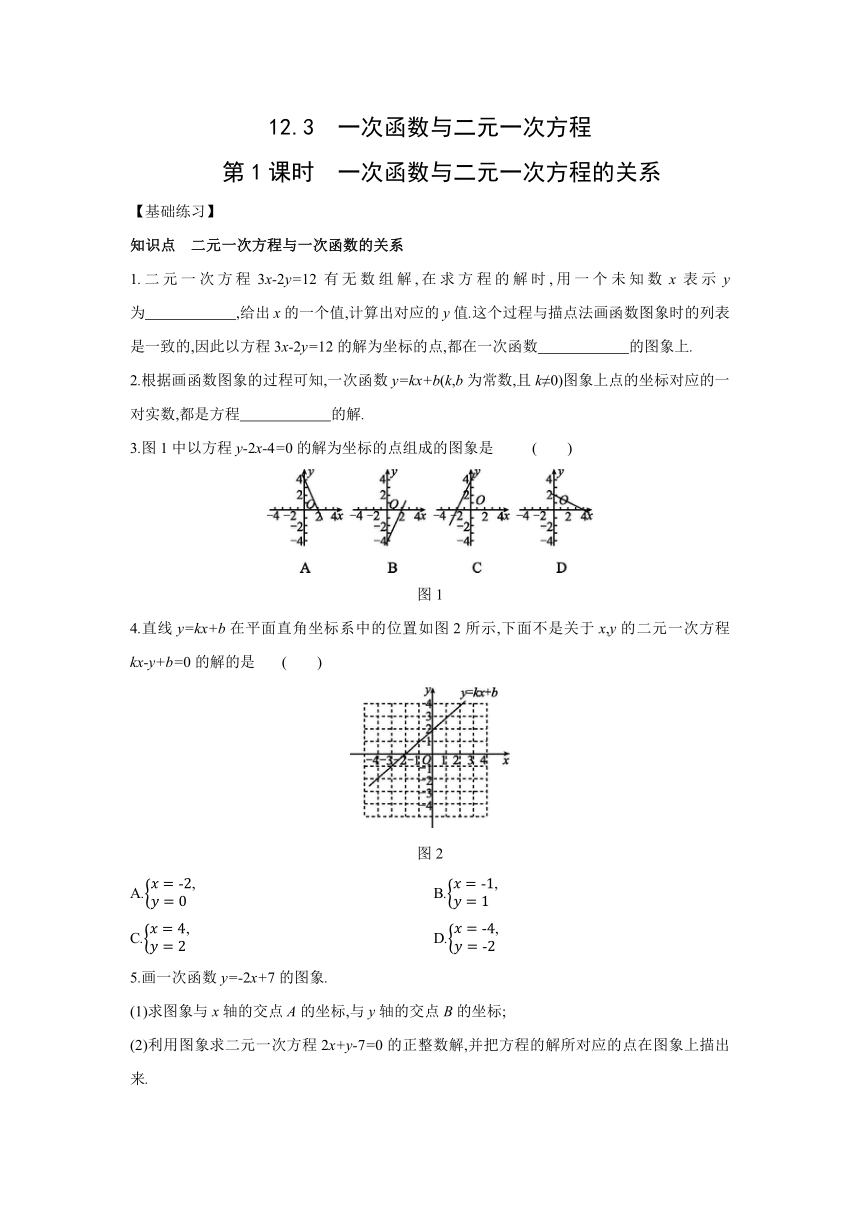
3.图1中以方程y-2x-4=0的解为坐标的点组成的图象是 ( )
图1
4.直线y=kx+b在平面直角坐标系中的位置如图2所示,下面不是关于x,y的二元一次方程kx-y+b=0的解的是 ( )
图2
A.x=-2,y=0 B.x=-1,y=1
C.x=4,y=2 D.x=-4,y=-2
5.画一次函数y=-2x+7的图象.
(1)求图象与x轴的交点A的坐标,与y轴的交点B的坐标;
(2)利用图象求二元一次方程2x+y-7=0的正整数解,并把方程的解所对应的点在图象上描出来.
【能力提升】
6.已知x=1,y=-1是方程y-(kx+1)=0的一个解,则直线y=kx+1不经过的象限是( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
7.若以二元一次方程x+2y-b=0的解为坐标的点(x,y)都在直线y=-12x+b-1上,则常数b的值为( )
A.12 B.2 C.-1 D.1
8.已知一支水笔3元,一个练习本1元,晓华买水笔和练习本(两种都要买)共花了10元钱,他买了多少支水笔?多少个练习本?请你用图象法求解.
9.在平面直角坐标系中,直线l1经过点(2,3)和(-1,-3),直线l2经过原点,且与直线l1交于点(-2,a).
(1)a= ;?
(2)(-2,a)可以看成哪两个二元一次方程的公共解?
(3)设直线l1与直线l2的交点为P,直线l1与y轴交于点A,请你求出三角形APO的面积.
第2课时 二元一次方程组的图象解法
【基础练习】
知识点 1 用图象法解方程组
1.如图3,已知直线y=-x+4与y=x+2的交点为P(1,3),验证x=1,y=3 方程组x+y=4,x-y=-2的解.(填“是”或“不是”)?
图3 图4
2.[2019·贵阳] 在同一平面直角坐标系内,一次函数y=k1x+b1与y=k2x+b2的图象如图4所示,则关于x,y的方程组y-k1x=b1,y-k2x=b2的解是 .?
3.用图象法解方程组x-2y=4,2x+y=4时,下列选项中的图象正确的是( )
图5
知识点 2 二元一次方程组解的情况与系数比的关系
4.由于直线y=2x-1与y=2x+5平行,则方程组2x-y=1,-2x+y=5的解的情况是( )
A.有唯一解 B.无解
C.无数解 D.有限解
知识点 3 解方程组求两条直线的交点坐标
5.求直线y=-2x+7与直线y=x+1的交点坐标,可以解方程组 ,得到交点的坐标为 .?
6.已知方程组2x-y+3=0,ax-y+c=0的解为x=-1,y=1,则一次函数y=2x+3与y=ax+c的图象的交点坐标是( )
A.(-1,1) B.(1,-1)
C.(2,-2) D.(-2,2)
【能力提升】
7.利用图象法解关于x,y的方程组mx+y=1,4x-ny=3时,若表示两方程的直线重合,则m= ,n= ;若表示两方程的直线平行,则mn= 且n .?
8.[教材习题12.3第3题变式题] 在图6所示的同一平面直角坐标系内画出一次函数y1=-x+4和y2=2x-5的图象,根据图象回答下列问题:
(1)求方程组y=-x+4,y=2x-5的解;
(2)当x取何值时,y1>y2?当x取何值时,y1>0且y2<0?
图6
9.如图7,直线m:3x+3y=12与x轴交于点A,与y轴交于点B,直线n:ax+by=-5与x轴交于点C(-53,0),与直线m交于点P,若点P的横坐标为1.
(1)求A,B两点的坐标;
(2)直接写出方程组3x+3y=12,ax+by=-5的解;
(3)求a和b的值;
(4)求三角形PAC的面积.
图7
答案
第一课时
1.y=32x-6 y=32x-6
2.kx-y+b=0
3.C
4.C [解析] 由于点(4,2)不在函数y=kx+b的图象上,故x=4,y=2不是二元一次方程kx-y+b=0的解.
5.解:如图所示.
(1)当y=0时,-2x+7=0,解得x=3.5.
当x=0时,y=7.
所以点A,B的坐标分别为(3.5,0),(0,7).
(2)结合图象,方程2x+y-7=0的正整数解是x1=1,y1=5,x2=2,y2=3,x3=3,y3=1.
描点如图所示.
6.C [解析] 把方程的解代入方程中,得k=-2,则直线y=-2x+1不经过第三象限.
7.B [解析] 以二元一次方程x+2y-b=0的解为坐标的点(x,y)都在直线y=-12x+b-1上,化简二元一次方程,得y=-12x+12b,即12b=b-1,解得b=2.故选B.
8.解:设他买了x支水笔,y个练习本,则有y=10-3x.
(1)列表:
x
1
2
y
7
4
(2)描点,连线,在平面直角坐标系中画出函数的图象,图象略.
(3)观察图象,点(1,7),(2,4),(3,1)在函数的图象上,即3x+y=10的正整数解为
x1=1,y1=7,x2=2,y2=4,x3=3,y3=1.
答:他买了1支水笔、7个练习本,或2支水笔、4个练习本,或3支水笔、1个练习本.
9.解:(1)设直线l1的函数表达式为y=kx+b.把(2,3),(-1,-3)分别代入,
得2k+b=3,-k+b=-3,解得k=2,b=-1,
所以直线l1的函数表达式为y=2x-1.
当x=-2时,y=-4-1=-5,
即a=-5.
(2)设直线l2的函数表达式为y=k1x.
把(-2,-5)代入,得-5=-2k1,解得k1=52,
所以直线l2的函数表达式为y=52x.
所以(-2,-5)可以看成是二元一次方程2x-y=1与52x-y=0的公共解.
(3)如图,把x=0代入y=2x-1,得y=-1.
所以点A的坐标为(0,-1).
又因为P(-2,-5),
所以S三角形APO=12·OA·|-2|=12×|-1|×2=12×1×2=1.
第二课时
1.是
2.x=2,y=1 [解析] 因为一次函数y=k1x+b1与y=k2x+b2的图象的交点坐标是(2,1),所以关于x,y的方程组y-k1x=b1,y-k2x=b2的解是x=2,y=1.
3.C
4.B [解析] 由于两条直线平行,没有交点,所以对应的方程组2x-y=1,-2x+y=5无解.
5.2x+y=7,-x+y=1 (2,3)
6.A [解析] 一次函数的表达式y=2x+3,y=ax+c化成二元一次方程的形式分别为2x-y+3=0,ax-y+c=0,两个一次函数图象的交点坐标就是由两个二元一次方程组成的方程组的解.因为方程组的解是x=-1,y=1,故两函数图象的交点坐标为(-1,1).
故选A.
7.43 -3 -4 ≠-3 [解析] 将两个二元一次方程化为y=-mx+1,y=4nx-3n,若表示两方程的直线重合,则有-m=4n,1=-3n,所以m=43,n=-3;
若表示两方程的直线平行,则有-m=4n,1≠-3n,
所以mn=-4且n≠-3.
8.解:如图所示.
(1)由图象可知,直线y1=-x+4与直线y2=2x-5的交点坐标是(3,1),所以方程组y=-x+4,y=2x-5的解为x=3,y=1.
(2)由图可知,当x<3时,y1>y2;
当x<2.5时,y1>0且y2<0.
9.解:(1)令3x+3y=12中y=0,则3x=12,
解得x=4,所以点A的坐标为(4,0).
令3x+3y=12中x=0,则3y=12,
解得y=4,所以点B的坐标为(0,4).
(2)令3x+3y=12中x=1,则3+3y=12,
解得y=3,所以点P的坐标为(1,3).
所以方程组3x+3y=12,ax+by=-5的解是x=1,y=3.
(3)将C-53,0,P(1,3)代入ax+by=-5中,得-53a=-5,a+3b=-5,解得a=3,b=-83.
(4)AC=4--53=173,
所以S三角形PAC=12×173×3=8.5.
第1课时 一次函数与二元一次方程的关系
【基础练习】
知识点 二元一次方程与一次函数的关系
1.二元一次方程3x-2y=12有无数组解,在求方程的解时,用一个未知数x表示y为 ,给出x的一个值,计算出对应的y值.这个过程与描点法画函数图象时的列表是一致的,因此以方程3x-2y=12的解为坐标的点,都在一次函数 的图象上.?
2.根据画函数图象的过程可知,一次函数y=kx+b(k,b为常数,且k≠0)图象上点的坐标对应的一对实数,都是方程 的解.?
3.图1中以方程y-2x-4=0的解为坐标的点组成的图象是 ( )
图1
4.直线y=kx+b在平面直角坐标系中的位置如图2所示,下面不是关于x,y的二元一次方程kx-y+b=0的解的是 ( )
图2
A.x=-2,y=0 B.x=-1,y=1
C.x=4,y=2 D.x=-4,y=-2
5.画一次函数y=-2x+7的图象.
(1)求图象与x轴的交点A的坐标,与y轴的交点B的坐标;
(2)利用图象求二元一次方程2x+y-7=0的正整数解,并把方程的解所对应的点在图象上描出来.
【能力提升】
6.已知x=1,y=-1是方程y-(kx+1)=0的一个解,则直线y=kx+1不经过的象限是( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
7.若以二元一次方程x+2y-b=0的解为坐标的点(x,y)都在直线y=-12x+b-1上,则常数b的值为( )
A.12 B.2 C.-1 D.1
8.已知一支水笔3元,一个练习本1元,晓华买水笔和练习本(两种都要买)共花了10元钱,他买了多少支水笔?多少个练习本?请你用图象法求解.
9.在平面直角坐标系中,直线l1经过点(2,3)和(-1,-3),直线l2经过原点,且与直线l1交于点(-2,a).
(1)a= ;?
(2)(-2,a)可以看成哪两个二元一次方程的公共解?
(3)设直线l1与直线l2的交点为P,直线l1与y轴交于点A,请你求出三角形APO的面积.
第2课时 二元一次方程组的图象解法
【基础练习】
知识点 1 用图象法解方程组
1.如图3,已知直线y=-x+4与y=x+2的交点为P(1,3),验证x=1,y=3 方程组x+y=4,x-y=-2的解.(填“是”或“不是”)?
图3 图4
2.[2019·贵阳] 在同一平面直角坐标系内,一次函数y=k1x+b1与y=k2x+b2的图象如图4所示,则关于x,y的方程组y-k1x=b1,y-k2x=b2的解是 .?
3.用图象法解方程组x-2y=4,2x+y=4时,下列选项中的图象正确的是( )
图5
知识点 2 二元一次方程组解的情况与系数比的关系
4.由于直线y=2x-1与y=2x+5平行,则方程组2x-y=1,-2x+y=5的解的情况是( )
A.有唯一解 B.无解
C.无数解 D.有限解
知识点 3 解方程组求两条直线的交点坐标
5.求直线y=-2x+7与直线y=x+1的交点坐标,可以解方程组 ,得到交点的坐标为 .?
6.已知方程组2x-y+3=0,ax-y+c=0的解为x=-1,y=1,则一次函数y=2x+3与y=ax+c的图象的交点坐标是( )
A.(-1,1) B.(1,-1)
C.(2,-2) D.(-2,2)
【能力提升】
7.利用图象法解关于x,y的方程组mx+y=1,4x-ny=3时,若表示两方程的直线重合,则m= ,n= ;若表示两方程的直线平行,则mn= 且n .?
8.[教材习题12.3第3题变式题] 在图6所示的同一平面直角坐标系内画出一次函数y1=-x+4和y2=2x-5的图象,根据图象回答下列问题:
(1)求方程组y=-x+4,y=2x-5的解;
(2)当x取何值时,y1>y2?当x取何值时,y1>0且y2<0?
图6
9.如图7,直线m:3x+3y=12与x轴交于点A,与y轴交于点B,直线n:ax+by=-5与x轴交于点C(-53,0),与直线m交于点P,若点P的横坐标为1.
(1)求A,B两点的坐标;
(2)直接写出方程组3x+3y=12,ax+by=-5的解;
(3)求a和b的值;
(4)求三角形PAC的面积.
图7
答案
第一课时
1.y=32x-6 y=32x-6
2.kx-y+b=0
3.C
4.C [解析] 由于点(4,2)不在函数y=kx+b的图象上,故x=4,y=2不是二元一次方程kx-y+b=0的解.
5.解:如图所示.
(1)当y=0时,-2x+7=0,解得x=3.5.
当x=0时,y=7.
所以点A,B的坐标分别为(3.5,0),(0,7).
(2)结合图象,方程2x+y-7=0的正整数解是x1=1,y1=5,x2=2,y2=3,x3=3,y3=1.
描点如图所示.
6.C [解析] 把方程的解代入方程中,得k=-2,则直线y=-2x+1不经过第三象限.
7.B [解析] 以二元一次方程x+2y-b=0的解为坐标的点(x,y)都在直线y=-12x+b-1上,化简二元一次方程,得y=-12x+12b,即12b=b-1,解得b=2.故选B.
8.解:设他买了x支水笔,y个练习本,则有y=10-3x.
(1)列表:
x
1
2
y
7
4
(2)描点,连线,在平面直角坐标系中画出函数的图象,图象略.
(3)观察图象,点(1,7),(2,4),(3,1)在函数的图象上,即3x+y=10的正整数解为
x1=1,y1=7,x2=2,y2=4,x3=3,y3=1.
答:他买了1支水笔、7个练习本,或2支水笔、4个练习本,或3支水笔、1个练习本.
9.解:(1)设直线l1的函数表达式为y=kx+b.把(2,3),(-1,-3)分别代入,
得2k+b=3,-k+b=-3,解得k=2,b=-1,
所以直线l1的函数表达式为y=2x-1.
当x=-2时,y=-4-1=-5,
即a=-5.
(2)设直线l2的函数表达式为y=k1x.
把(-2,-5)代入,得-5=-2k1,解得k1=52,
所以直线l2的函数表达式为y=52x.
所以(-2,-5)可以看成是二元一次方程2x-y=1与52x-y=0的公共解.
(3)如图,把x=0代入y=2x-1,得y=-1.
所以点A的坐标为(0,-1).
又因为P(-2,-5),
所以S三角形APO=12·OA·|-2|=12×|-1|×2=12×1×2=1.
第二课时
1.是
2.x=2,y=1 [解析] 因为一次函数y=k1x+b1与y=k2x+b2的图象的交点坐标是(2,1),所以关于x,y的方程组y-k1x=b1,y-k2x=b2的解是x=2,y=1.
3.C
4.B [解析] 由于两条直线平行,没有交点,所以对应的方程组2x-y=1,-2x+y=5无解.
5.2x+y=7,-x+y=1 (2,3)
6.A [解析] 一次函数的表达式y=2x+3,y=ax+c化成二元一次方程的形式分别为2x-y+3=0,ax-y+c=0,两个一次函数图象的交点坐标就是由两个二元一次方程组成的方程组的解.因为方程组的解是x=-1,y=1,故两函数图象的交点坐标为(-1,1).
故选A.
7.43 -3 -4 ≠-3 [解析] 将两个二元一次方程化为y=-mx+1,y=4nx-3n,若表示两方程的直线重合,则有-m=4n,1=-3n,所以m=43,n=-3;
若表示两方程的直线平行,则有-m=4n,1≠-3n,
所以mn=-4且n≠-3.
8.解:如图所示.
(1)由图象可知,直线y1=-x+4与直线y2=2x-5的交点坐标是(3,1),所以方程组y=-x+4,y=2x-5的解为x=3,y=1.
(2)由图可知,当x<3时,y1>y2;
当x<2.5时,y1>0且y2<0.
9.解:(1)令3x+3y=12中y=0,则3x=12,
解得x=4,所以点A的坐标为(4,0).
令3x+3y=12中x=0,则3y=12,
解得y=4,所以点B的坐标为(0,4).
(2)令3x+3y=12中x=1,则3+3y=12,
解得y=3,所以点P的坐标为(1,3).
所以方程组3x+3y=12,ax+by=-5的解是x=1,y=3.
(3)将C-53,0,P(1,3)代入ax+by=-5中,得-53a=-5,a+3b=-5,解得a=3,b=-83.
(4)AC=4--53=173,
所以S三角形PAC=12×173×3=8.5.
