15.2线段的垂直平分线练习题 2021——2022学年沪科版八年级数学上册(Word版 含答案)
文档属性
| 名称 | 15.2线段的垂直平分线练习题 2021——2022学年沪科版八年级数学上册(Word版 含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 147.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-30 14:38:25 | ||
图片预览



文档简介
15.2 线段的垂直平分线
【基础练习】
知识点 1 线段垂直平分线的画法
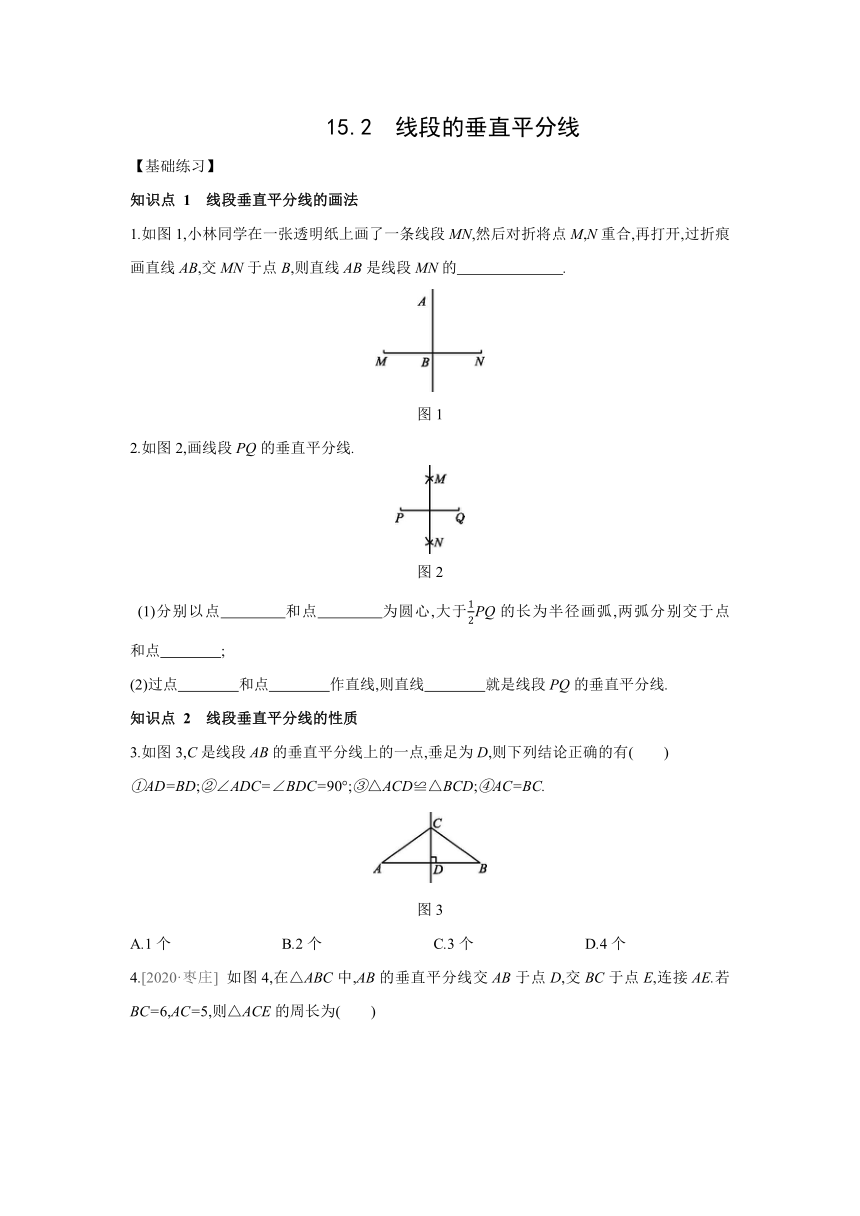
1.如图1,小林同学在一张透明纸上画了一条线段MN,然后对折将点M,N重合,再打开,过折痕画直线AB,交MN于点B,则直线AB是线段MN的 .?
图1
2.如图2,画线段PQ的垂直平分线.
图2
(1)分别以点 和点 为圆心,大于12PQ的长为半径画弧,两弧分别交于点 和点 ;?
(2)过点 和点 作直线,则直线 就是线段PQ的垂直平分线.?
知识点 2 线段垂直平分线的性质
3.如图3,C是线段AB的垂直平分线上的一点,垂足为D,则下列结论正确的有( )
①AD=BD;②∠ADC=∠BDC=90°;③△ACD≌△BCD;④AC=BC.
图3
A.1个 B.2个 C.3个 D.4个
4.[2020·枣庄] 如图4,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E,连接AE.若BC=6,AC=5,则△ACE的周长为( )
图4
A.8 B.11 C.16 D.17
5.如图5,在△ABC中,AC=4 cm,线段AB的垂直平分线交AC于点N,交AB于点M,△BCN的周长是7 cm,则BC的长为( )
图5
A.1 cm B.2 cm C.3 cm D.4 cm
6.[2020·合肥瑶海区期末] 如图6,在△ABC中,DE垂直平分AC,交AC于点E,交BC于点D,连接AD,AE=4 cm,则△ABC的周长与△ABD的周长的差为( )
图6
A.2 cm B.4 cm C.6 cm D.8 cm
知识点 3 线段垂直平分线的判定
7.已知线段AB外有两点M,N,且MA=MB,NA=NB,直线MN交线段AB于点O,则点O是线段AB的 ,直线MN是线段AB的 .若直线MN上另有一点P,则PA与PB的数量关系是 ,你的依据是 .?
8.如图7,AC=AD,BC=BD,则有( )
图7
A.AB垂直平分CD B.CD垂直平分AB
C.AB与CD互相垂直平分 D.CD平分∠ACB
9.下列条件不能判定直线MN是线段AB的垂直平分线的是( )
A.MA=MB,NA=NB B.MA=MB,MN⊥AB
C.MA=NA,MB=NB D.MA=MB,MN平分AB且点M不在AB上
10.如图8,AB=AC,MB=MC.求证:直线AM是线段BC的垂直平分线.
图8
【能力提升】
11.如图9,在△ABC中,D是AB的中点,且CD⊥AB,若∠A=45°,则∠B= °.?
图9
12.如图10所示,在△ABC中,AB=AC,AB的垂直平分线DE交BC的延长线于点E,交AC于点F,交AB于点D,∠A=50°,AB+BC=6,则△BCF的周长为 ,∠EFC= °.?
图10
13.如图11,AD垂直平分BC于点D,EF垂直平分AB于点F,点E在AC上,BE+CE=20 cm,则AB= cm.?
图11
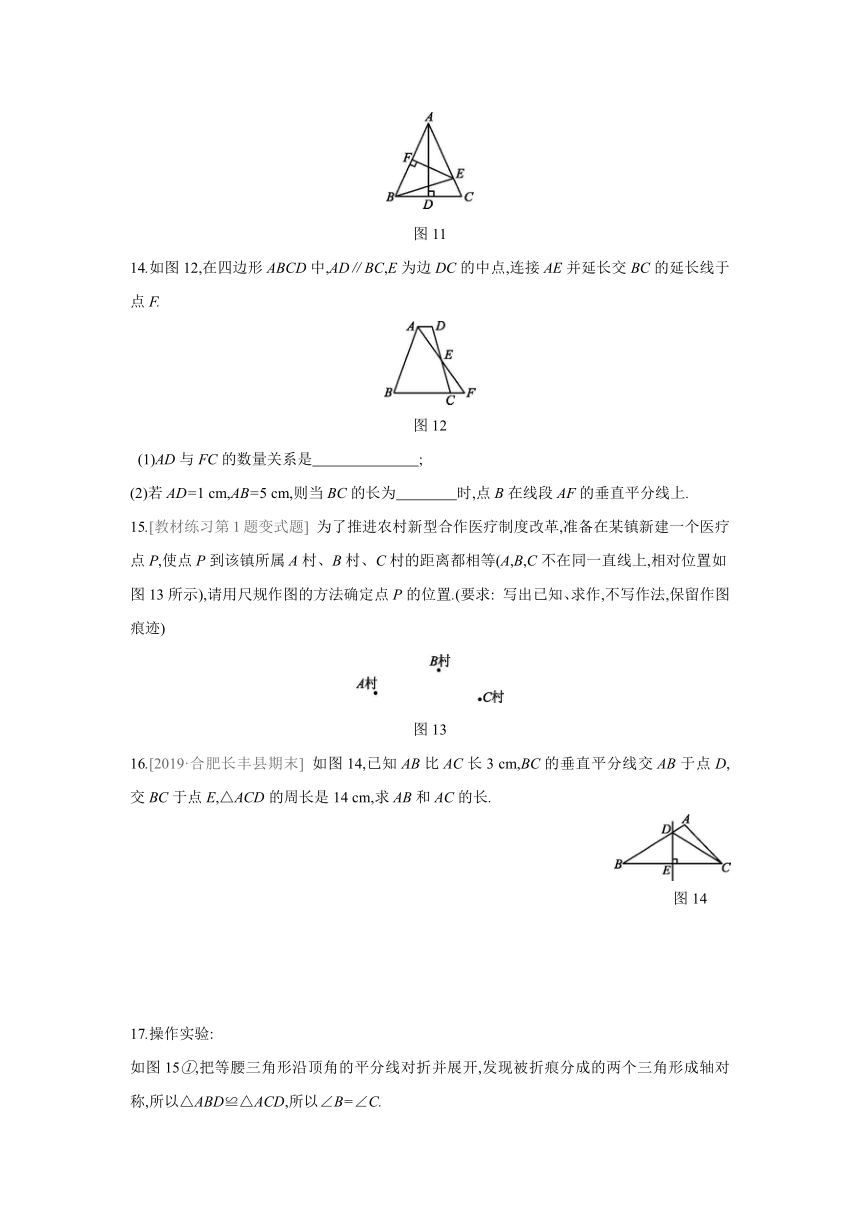
14.如图12,在四边形ABCD中,AD∥BC,E为边DC的中点,连接AE并延长交BC的延长线于点F.
图12
(1)AD与FC的数量关系是 ;?
(2)若AD=1 cm,AB=5 cm,则当BC的长为 时,点B在线段AF的垂直平分线上.?
15.[教材练习第1题变式题] 为了推进农村新型合作医疗制度改革,准备在某镇新建一个医疗点P,使点P到该镇所属A村、B村、C村的距离都相等(A,B,C不在同一直线上,相对位置如图13所示),请用尺规作图的方法确定点P的位置.(要求: 写出已知、求作,不写作法,保留作图痕迹)
图13
16.[2019·合肥长丰县期末] 如图14,已知AB比AC长3 cm,BC的垂直平分线交AB于点D,交BC于点E,△ACD的周长是14 cm,求AB和AC的长.
图14
17.操作实验:
如图15①,把等腰三角形沿顶角的平分线对折并展开,发现被折痕分成的两个三角形成轴对称,所以△ABD≌△ACD,所以∠B=∠C.
归纳结论:如果一个三角形有两条边相等,那么这两条边所对的角也相等(证明略).
探究应用:如图15②,CB⊥AB,垂足为B,DA⊥AB,垂足为A,E为AB的中点,AB=BC,
CE⊥BD.
(1)BE与AD是否相等,为什么?
(2)小明认为AC是线段DE的垂直平分线,你认为对吗?说说你的理由;
(3)∠DBC与∠DCB相等吗?试说明理由.
图15
答案
1.垂直平分线
2.(1)P Q M N (2)M N MN
3.D [解析] ∵CD是线段AB的垂直平分线,
∴AD=BD,∠ADC=∠BDC=90°,故①②正确;
又∵CD=CD(公共边),
∴△ACD≌△BCD,故③正确;
由③可得④正确(也可直接根据线段垂直平分线上的点到线段两端的距离相等,得出④正确).
4.B [解析] ∵DE垂直平分AB,∴AE=BE,
∴△ACE的周长=AC+CE+AE=AC+CE+BE=AC+BC=5+6=11.
5.C [解析] ∵MN是线段AB的垂直平分线,∴AN=BN.
∵△BCN的周长=BN+NC+BC=7 cm,
∴AN+NC+BC=7 cm,
∴AC+BC=7 cm,
∴BC=7-4=3(cm).
6.D [解析] ∵DE垂直平分AC,AE=4 cm,
∴AD=CD,AC=2AE=8 cm.
∵△ABC的周长=AB+AC+BC,△ABD的周长=AB+AD+BD=AB+BC,
∴△ABC的周长与△ABD的周长的差为AC=8 cm.
7.中点 垂直平分线 PA=PB 线段垂直平分线上的点到线段两端的距离相等
8.A 9.C
10.证明:∵AB=AC,
∴点A在线段BC的垂直平分线上.
∵MB=MC,
∴点M在线段BC的垂直平分线上.
∴直线AM是线段BC的垂直平分线.
11.45 [解析] ∵D是AB的中点,CD⊥AB,
∴CD是线段AB的垂直平分线,
∴AC=BC.易证Rt△ACD≌Rt△BCD,
∴∠B=∠A=45°.
12.6 40 [解析] 因为直线DE为边AB的垂直平分线,所以AF=BF.所以△BCF的周长=CF+BF+BC=CF+AF+BC=AC+BC=AB+BC=6.∠EFC=∠AFD=90°-∠A=90°-50°=40°.
13.20 [解析] ∵EF垂直平分AB于点F,
∴AE=BE.
∵BE+CE=20 cm,
∴AE+CE=20 cm,
即AC=20 cm.
∵AD垂直平分BC于点D,
∴AB=AC=20 cm.
14.(1)AD=FC (2)4 cm
[解析] (1)因为AD∥BC,
所以∠D=∠ECF.
因为E为边DC的中点,
所以DE=CE.
在△ADE和△FCE中,
因为∠D=∠ECF,DE=CE,∠AED=∠FEC,
所以△ADE≌△FCE.所以AD=FC.
(2)因为点B在线段AF的垂直平分线上,
所以AB=BF.
又因为AB=5 cm,FC=AD=1 cm,
所以BC=BF-FC=5-1=4(cm),
即当BC=4 cm时,点B在线段AF的垂直平分线上.
15.解:已知:A,B,C三点不在同一直线上.
求作:一点P,使PA=PB=PC.
如图所示,点P即为所求.
16.解:∵DE是BC的垂直平分线,
∴CD=BD,
∴△ACD的周长=AC+CD+AD=AC+BD+AD=AC+AB.
由题意得AB-AC=3,AB+AC=14,解得AC=5.5,AB=8.5,
∴AB和AC的长分别为8.5 cm,5.5 cm.
17.解:(1)BE=AD.理由:∵BD⊥EC,DA⊥AB,
∴∠BEC+∠ABD=90°,∠ADB+∠ABD=90°.
∴∠ADB=∠BEC.
在△ADB和△BEC中,
∵∠ADB=∠BEC,∠DAB=∠EBC=90°,AB=BC,
∴△ADB≌△BEC(AAS).
∴BE=AD.
(2)对.理由:∵E是AB的中点,∴AE=BE.
∵AD=BE,∴AE=AD.
在△ABC中,因为AB=BC,
∴∠BAC=∠BCA.
由题意易知AD∥BC,
∴∠DAC=∠BCA.
∴∠BAC=∠DAC.
在△ADC和△AEC中,
∵AD=AE,∠DAC=∠EAC,AC=AC,
∴△ADC≌△AEC(SAS).
∴DC=EC.
∴点C在线段DE的垂直平分线上.
∵AD=AE,
∴点A在线段DE的垂直平分线上.
∴AC是线段DE的垂直平分线.
(3)∠DBC=∠DCB.理由:
∵△ADB≌△BEC,
∴BD=EC.
又∵DC=EC,
∴DC=BD.
∴∠DBC=∠DCB.
【基础练习】
知识点 1 线段垂直平分线的画法
1.如图1,小林同学在一张透明纸上画了一条线段MN,然后对折将点M,N重合,再打开,过折痕画直线AB,交MN于点B,则直线AB是线段MN的 .?
图1
2.如图2,画线段PQ的垂直平分线.
图2
(1)分别以点 和点 为圆心,大于12PQ的长为半径画弧,两弧分别交于点 和点 ;?
(2)过点 和点 作直线,则直线 就是线段PQ的垂直平分线.?
知识点 2 线段垂直平分线的性质
3.如图3,C是线段AB的垂直平分线上的一点,垂足为D,则下列结论正确的有( )
①AD=BD;②∠ADC=∠BDC=90°;③△ACD≌△BCD;④AC=BC.
图3
A.1个 B.2个 C.3个 D.4个
4.[2020·枣庄] 如图4,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E,连接AE.若BC=6,AC=5,则△ACE的周长为( )
图4
A.8 B.11 C.16 D.17
5.如图5,在△ABC中,AC=4 cm,线段AB的垂直平分线交AC于点N,交AB于点M,△BCN的周长是7 cm,则BC的长为( )
图5
A.1 cm B.2 cm C.3 cm D.4 cm
6.[2020·合肥瑶海区期末] 如图6,在△ABC中,DE垂直平分AC,交AC于点E,交BC于点D,连接AD,AE=4 cm,则△ABC的周长与△ABD的周长的差为( )
图6
A.2 cm B.4 cm C.6 cm D.8 cm
知识点 3 线段垂直平分线的判定
7.已知线段AB外有两点M,N,且MA=MB,NA=NB,直线MN交线段AB于点O,则点O是线段AB的 ,直线MN是线段AB的 .若直线MN上另有一点P,则PA与PB的数量关系是 ,你的依据是 .?
8.如图7,AC=AD,BC=BD,则有( )
图7
A.AB垂直平分CD B.CD垂直平分AB
C.AB与CD互相垂直平分 D.CD平分∠ACB
9.下列条件不能判定直线MN是线段AB的垂直平分线的是( )
A.MA=MB,NA=NB B.MA=MB,MN⊥AB
C.MA=NA,MB=NB D.MA=MB,MN平分AB且点M不在AB上
10.如图8,AB=AC,MB=MC.求证:直线AM是线段BC的垂直平分线.
图8
【能力提升】
11.如图9,在△ABC中,D是AB的中点,且CD⊥AB,若∠A=45°,则∠B= °.?
图9
12.如图10所示,在△ABC中,AB=AC,AB的垂直平分线DE交BC的延长线于点E,交AC于点F,交AB于点D,∠A=50°,AB+BC=6,则△BCF的周长为 ,∠EFC= °.?
图10
13.如图11,AD垂直平分BC于点D,EF垂直平分AB于点F,点E在AC上,BE+CE=20 cm,则AB= cm.?
图11
14.如图12,在四边形ABCD中,AD∥BC,E为边DC的中点,连接AE并延长交BC的延长线于点F.
图12
(1)AD与FC的数量关系是 ;?
(2)若AD=1 cm,AB=5 cm,则当BC的长为 时,点B在线段AF的垂直平分线上.?
15.[教材练习第1题变式题] 为了推进农村新型合作医疗制度改革,准备在某镇新建一个医疗点P,使点P到该镇所属A村、B村、C村的距离都相等(A,B,C不在同一直线上,相对位置如图13所示),请用尺规作图的方法确定点P的位置.(要求: 写出已知、求作,不写作法,保留作图痕迹)
图13
16.[2019·合肥长丰县期末] 如图14,已知AB比AC长3 cm,BC的垂直平分线交AB于点D,交BC于点E,△ACD的周长是14 cm,求AB和AC的长.
图14
17.操作实验:
如图15①,把等腰三角形沿顶角的平分线对折并展开,发现被折痕分成的两个三角形成轴对称,所以△ABD≌△ACD,所以∠B=∠C.
归纳结论:如果一个三角形有两条边相等,那么这两条边所对的角也相等(证明略).
探究应用:如图15②,CB⊥AB,垂足为B,DA⊥AB,垂足为A,E为AB的中点,AB=BC,
CE⊥BD.
(1)BE与AD是否相等,为什么?
(2)小明认为AC是线段DE的垂直平分线,你认为对吗?说说你的理由;
(3)∠DBC与∠DCB相等吗?试说明理由.
图15
答案
1.垂直平分线
2.(1)P Q M N (2)M N MN
3.D [解析] ∵CD是线段AB的垂直平分线,
∴AD=BD,∠ADC=∠BDC=90°,故①②正确;
又∵CD=CD(公共边),
∴△ACD≌△BCD,故③正确;
由③可得④正确(也可直接根据线段垂直平分线上的点到线段两端的距离相等,得出④正确).
4.B [解析] ∵DE垂直平分AB,∴AE=BE,
∴△ACE的周长=AC+CE+AE=AC+CE+BE=AC+BC=5+6=11.
5.C [解析] ∵MN是线段AB的垂直平分线,∴AN=BN.
∵△BCN的周长=BN+NC+BC=7 cm,
∴AN+NC+BC=7 cm,
∴AC+BC=7 cm,
∴BC=7-4=3(cm).
6.D [解析] ∵DE垂直平分AC,AE=4 cm,
∴AD=CD,AC=2AE=8 cm.
∵△ABC的周长=AB+AC+BC,△ABD的周长=AB+AD+BD=AB+BC,
∴△ABC的周长与△ABD的周长的差为AC=8 cm.
7.中点 垂直平分线 PA=PB 线段垂直平分线上的点到线段两端的距离相等
8.A 9.C
10.证明:∵AB=AC,
∴点A在线段BC的垂直平分线上.
∵MB=MC,
∴点M在线段BC的垂直平分线上.
∴直线AM是线段BC的垂直平分线.
11.45 [解析] ∵D是AB的中点,CD⊥AB,
∴CD是线段AB的垂直平分线,
∴AC=BC.易证Rt△ACD≌Rt△BCD,
∴∠B=∠A=45°.
12.6 40 [解析] 因为直线DE为边AB的垂直平分线,所以AF=BF.所以△BCF的周长=CF+BF+BC=CF+AF+BC=AC+BC=AB+BC=6.∠EFC=∠AFD=90°-∠A=90°-50°=40°.
13.20 [解析] ∵EF垂直平分AB于点F,
∴AE=BE.
∵BE+CE=20 cm,
∴AE+CE=20 cm,
即AC=20 cm.
∵AD垂直平分BC于点D,
∴AB=AC=20 cm.
14.(1)AD=FC (2)4 cm
[解析] (1)因为AD∥BC,
所以∠D=∠ECF.
因为E为边DC的中点,
所以DE=CE.
在△ADE和△FCE中,
因为∠D=∠ECF,DE=CE,∠AED=∠FEC,
所以△ADE≌△FCE.所以AD=FC.
(2)因为点B在线段AF的垂直平分线上,
所以AB=BF.
又因为AB=5 cm,FC=AD=1 cm,
所以BC=BF-FC=5-1=4(cm),
即当BC=4 cm时,点B在线段AF的垂直平分线上.
15.解:已知:A,B,C三点不在同一直线上.
求作:一点P,使PA=PB=PC.
如图所示,点P即为所求.
16.解:∵DE是BC的垂直平分线,
∴CD=BD,
∴△ACD的周长=AC+CD+AD=AC+BD+AD=AC+AB.
由题意得AB-AC=3,AB+AC=14,解得AC=5.5,AB=8.5,
∴AB和AC的长分别为8.5 cm,5.5 cm.
17.解:(1)BE=AD.理由:∵BD⊥EC,DA⊥AB,
∴∠BEC+∠ABD=90°,∠ADB+∠ABD=90°.
∴∠ADB=∠BEC.
在△ADB和△BEC中,
∵∠ADB=∠BEC,∠DAB=∠EBC=90°,AB=BC,
∴△ADB≌△BEC(AAS).
∴BE=AD.
(2)对.理由:∵E是AB的中点,∴AE=BE.
∵AD=BE,∴AE=AD.
在△ABC中,因为AB=BC,
∴∠BAC=∠BCA.
由题意易知AD∥BC,
∴∠DAC=∠BCA.
∴∠BAC=∠DAC.
在△ADC和△AEC中,
∵AD=AE,∠DAC=∠EAC,AC=AC,
∴△ADC≌△AEC(SAS).
∴DC=EC.
∴点C在线段DE的垂直平分线上.
∵AD=AE,
∴点A在线段DE的垂直平分线上.
∴AC是线段DE的垂直平分线.
(3)∠DBC=∠DCB.理由:
∵△ADB≌△BEC,
∴BD=EC.
又∵DC=EC,
∴DC=BD.
∴∠DBC=∠DCB.
