21.3二次函数与一元二次方程-课时作业 2021-2022学年沪科版数学九年级上册(Word版 含答案)
文档属性
| 名称 | 21.3二次函数与一元二次方程-课时作业 2021-2022学年沪科版数学九年级上册(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 207.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-30 00:00:00 | ||
图片预览

文档简介
21.3 二次函数与一元二次方程
知识点 1 二次函数与一元二次方程的关系
1.对抛物线y=ax2+bx+c,当b2-4ac>0时,抛物线与x轴有 个交点;当b2-4ac=0时,抛物线与x轴有 个交点;当b2-4ac<0时,抛物线与x轴有 个交点.?
2.[2019·荆门] 抛物线y=-x2+4x-4与坐标轴的交点个数为 ( )
A.0 B.1 C.2 D.3
3.[2019·合肥四十八中月考] 函数y=kx2-6x+3的图象与x轴有交点,则k的取值范围是 ( )
A.k<3 B.k<3且k≠0 C.k≤3 D.k≤3且k≠0
4.[2020·大连改编] 抛物线y=ax2+bx+c(a<0)与x轴的一个交点坐标为(-1,0),对称轴是直线x=1,其部分图象如图1所示,则一元二次方程ax2+bx+c=0的解为 .?
图1
5.[教材习题21.3第5题变式] 已知抛物线y=(k-8)x2-6x+k的顶点在x轴上,则k= .?
6.已知抛物线y=x2-5x-6与x轴交于A,B两点(点B在点A的右侧),与y轴交于点C,求△ABC的面积.
知识点 2 用图象法求一元二次方程的近似解
7.观察下表:
x
1.2
1.3
1.4
1.5
1.6
1.7
1.8
y=x2-
x-1
-0.76
-0.61
-0.44
-0.25
-0.04
0.19
0.44
结合表格,你认为一元二次方程x2-x-1=0的一个近似解是 ( )
A.x≈1.2 B.x≈1.4 C.x≈1.6 D.x≈1.8
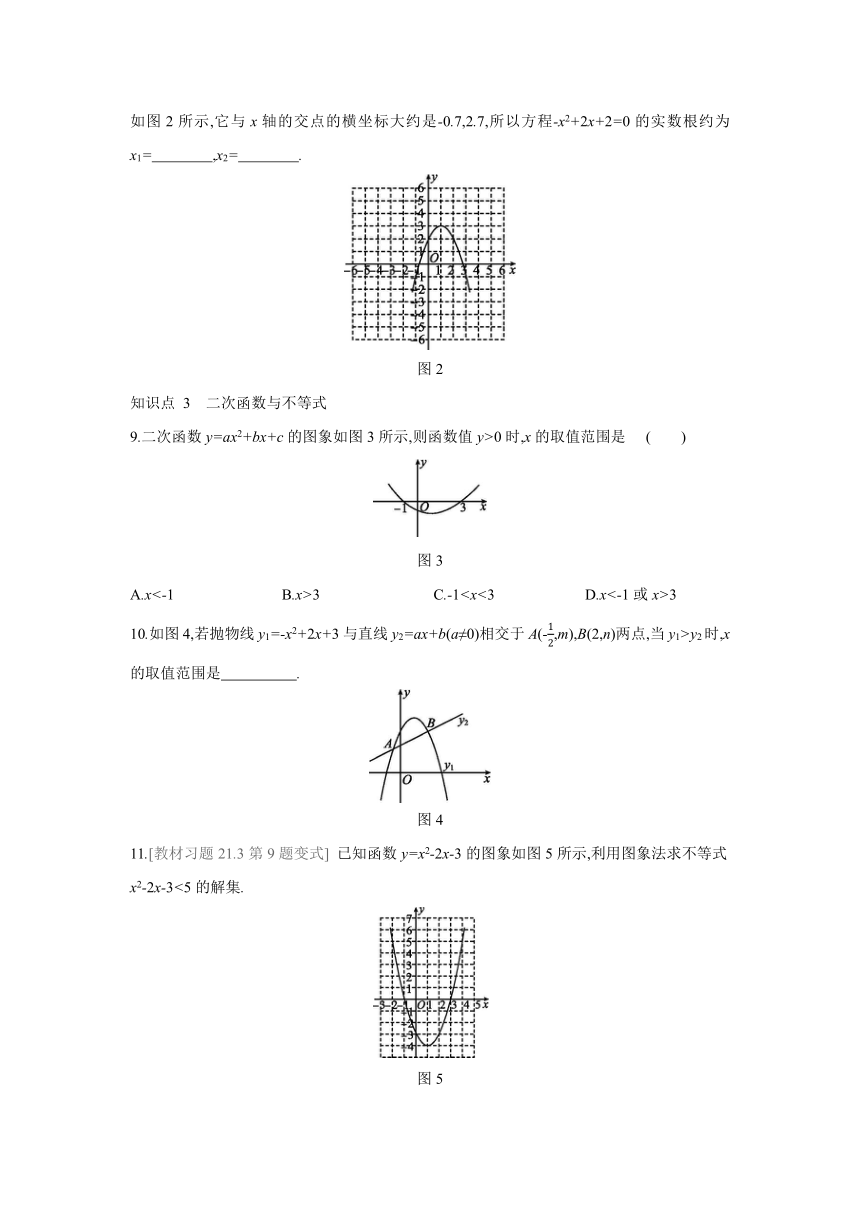
8.利用函数图象求方程-x2+2x+2=0的实数根(精确到0.1),要先作函数 的图象,如图2所示,它与x轴的交点的横坐标大约是-0.7,2.7,所以方程-x2+2x+2=0的实数根约为x1= ,x2= .?
图2
知识点 3 二次函数与不等式
9.二次函数y=ax2+bx+c的图象如图3所示,则函数值y>0时,x的取值范围是 ( )
图3
A.x<-1 B.x>3 C.-13
10.如图4,若抛物线y1=-x2+2x+3与直线y2=ax+b(a≠0)相交于A(-12,m),B(2,n)两点,当y1>y2时,x的取值范围是 .?
图4
11.[教材习题21.3第9题变式] 已知函数y=x2-2x-3的图象如图5所示,利用图象法求不等式x2-2x-3<5的解集.
图5
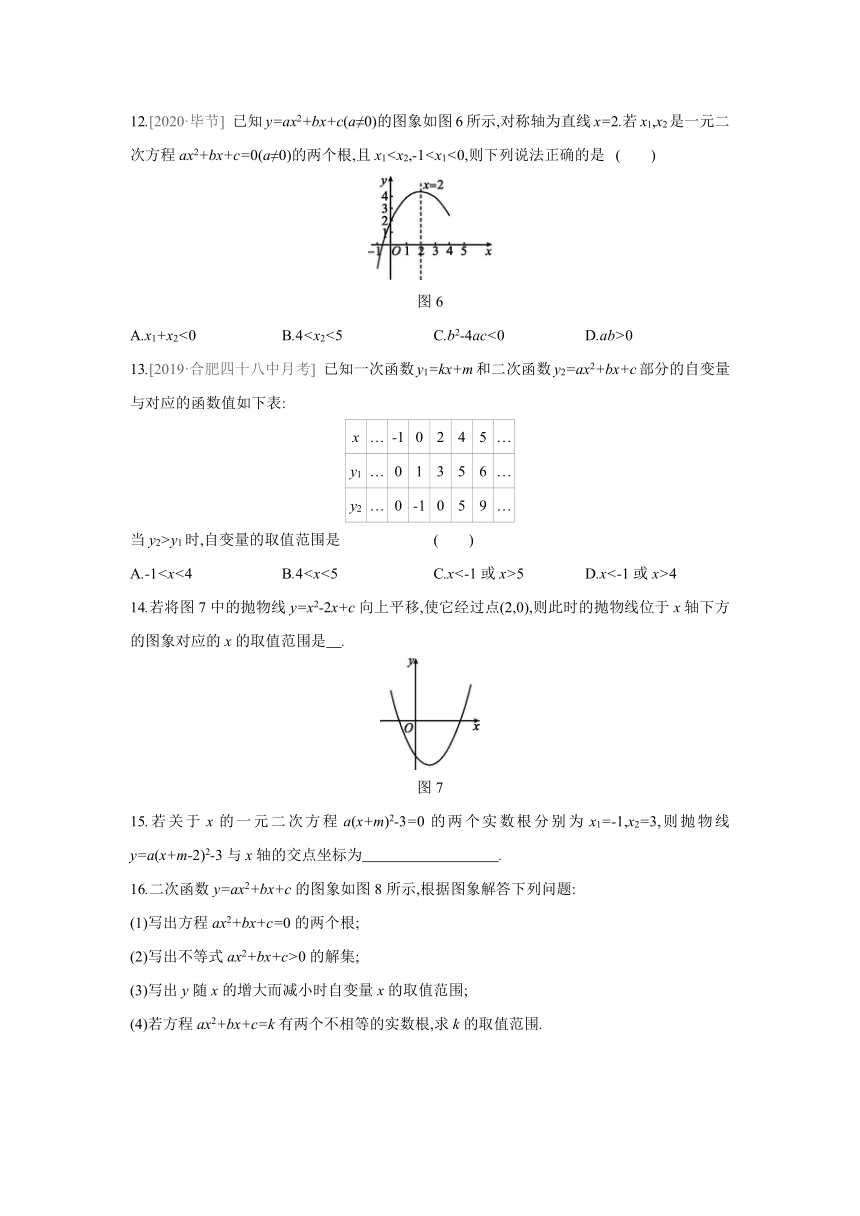
12.[2020·毕节] 已知y=ax2+bx+c(a≠0)的图象如图6所示,对称轴为直线x=2.若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两个根,且x1
图6
A.x1+x2<0 B.40
13.[2019·合肥四十八中月考] 已知一次函数y1=kx+m和二次函数y2=ax2+bx+c部分的自变量与对应的函数值如下表:
x
…
-1
0
2
4
5
…
y1
…
0
1
3
5
6
…
y2
…
0
-1
0
5
9
…
当y2>y1时,自变量的取值范围是 ( )
A.-15 D.x<-1或x>4
14.若将图7中的抛物线y=x2-2x+c向上平移,使它经过点(2,0),则此时的抛物线位于x轴下方的图象对应的x的取值范围是 .?
图7
15.若关于x的一元二次方程a(x+m)2-3=0的两个实数根分别为x1=-1,x2=3,则抛物线y=a(x+m-2)2-3与x轴的交点坐标为 .?
16.二次函数y=ax2+bx+c的图象如图8所示,根据图象解答下列问题:
(1)写出方程ax2+bx+c=0的两个根;
(2)写出不等式ax2+bx+c>0的解集;
(3)写出y随x的增大而减小时自变量x的取值范围;
(4)若方程ax2+bx+c=k有两个不相等的实数根,求k的取值范围.
图8
17.阅读下面的材料:
上课时李老师提出一个问题:对于任意实数x,关于x的不等式x2-2x-1-a>0恒成立,求a的取值范围.
小捷的思路是原不等式等价于x2-2x-1>a,设函数y1=x2-2x-1,y2=a,画出两个函数的图象的示意图,于是原问题转化为求函数y1的图象在y2的图象上方时a的取值范围.
(1)请结合小捷的思路回答:
对于任意实数x,关于x的不等式x2-2x-1-a>0恒成立,则a的取值范围是 ;?
(2)参考小捷思考问题的方法,解决问题:
关于x的方程x-4=a-3x在0教师详解详析
1.两 一 零
2.C [解析] 当x=0时,y=-x2+4x-4=-4,则抛物线与y轴的交点坐标为(0,-4).当y=0时,-x2+4x-4=0,解得x1=x2=2,抛物线与x轴的交点坐标为(2,0),所以抛物线与坐标轴有2个交点.故选C.
3.C [解析] 当k≠0时,抛物线与x轴有交点,则Δ=36-4k×3≥0,解得k≤3,且k≠0;当k=0时,一次函数y=-6x+3的图象与x轴有交点,因此k≤3.故选C.
4.x1=-1,x2=3 [解析] 由题意可知,抛物线与x轴的另一个交点坐标是(3,0),故该方程的两个解为x1=-1,x2=3.
5.9或-1 [解析] 抛物线的顶点在x轴上,则Δ=0,∴36-4k(k-8)=0,且k-8≠0,解得k1=9,k2=-1.故答案为9或-1.
6.[解析] 欲求△ABC的面积,必须先求出A,B,C三点的坐标.
解:令y=0,得一元二次方程x2-5x-6=0,解方程,得x1=6,x2=-1,
∴抛物线y=x2-5x-6与x轴的交点B,A的坐标分别为(6,0),(-1,0).
把x=0代入y=x2-5x-6,得y=-6,
∴点C的坐标为(0,-6).
∴S△ABC=12AB·OC=12×(6+1)×6=21.
7.C
8.y=-x2+2x+2 -0.7 2.7
9.D
10.-1211.解:如图,在平面直角坐标系中作出直线y=5,观察直线y=5与抛物线y=x2-2x-3的两个交点坐标为(-2,5)和(4,5),在直线y=5的下方,y=x2-2x-3的函数值都小于5,故不等式x2-2x-3<5的解集为-212.B [解析] ∵x1,x2是一元二次方程ax2+bx+c=0的两个根,
∴x1,x2是抛物线与x轴交点的横坐标.
∵抛物线的对称轴为直线x=2,
∴x1+x22=2,即x1+x2=4>0,故选项A错误;
∵x1∴-1<4-x2<0,
解得4∵抛物线与x轴有两个交点,
∴b2-4ac>0,故选项C错误;
∵抛物线开口向下,
∴a<0.
∵抛物线的对称轴为直线x=2,
∴-b2a=2,
∴b=-4a>0,
∴ab<0,故选项D错误.
故选B.
13.D [解析] ∵当x=-1时,y1=y2=0;当x=4时,y1=y2=5,∴直线与抛物线的交点为(-1,0)和(4,5),而-1y2,∴当y2>y1时,自变量x的取值范围是x<-1或x>4.
故选D.
14.015.(1,0),(5,0) [解析] 关于x的一元二次方程a(x+m)2-3=0的两个实数根分别为x1=-1,x2=3,即抛物线y=a(x+m)2-3与x轴的两个交点坐标是(-1,0),(3,0).抛物线y=a(x+m-2)2-3是将抛物线y=a(x+m)2-3向右平移2个单位得到的,故抛物线y=a(x+m-2)2-3与x轴的交点坐标是(1,0),(5,0).
16.解:(1)由图象可得,方程ax2+bx+c=0的两个根分别为x1=1,x2=3.
(2)由图象可知,当y=ax2+bx+c>0时,x的取值范围为1∴不等式ax2+bx+c>0的解集为1(3)由图象可知,当y随x的增大而减小时,自变量x的取值范围为x>2.
(4)方程ax2+bx+c=k有两个不相等的实数根,实际上就是二次函数y=ax2+bx+c的图象与直线y=k有两个交点,由图象可知,此时k的取值范围是k<2.
17.解:(1)a<-2
(2)将原方程转化为x2-4x+3=a,设y1=x2-4x+3,y2=a,记函数y1在0
知识点 1 二次函数与一元二次方程的关系
1.对抛物线y=ax2+bx+c,当b2-4ac>0时,抛物线与x轴有 个交点;当b2-4ac=0时,抛物线与x轴有 个交点;当b2-4ac<0时,抛物线与x轴有 个交点.?
2.[2019·荆门] 抛物线y=-x2+4x-4与坐标轴的交点个数为 ( )
A.0 B.1 C.2 D.3
3.[2019·合肥四十八中月考] 函数y=kx2-6x+3的图象与x轴有交点,则k的取值范围是 ( )
A.k<3 B.k<3且k≠0 C.k≤3 D.k≤3且k≠0
4.[2020·大连改编] 抛物线y=ax2+bx+c(a<0)与x轴的一个交点坐标为(-1,0),对称轴是直线x=1,其部分图象如图1所示,则一元二次方程ax2+bx+c=0的解为 .?
图1
5.[教材习题21.3第5题变式] 已知抛物线y=(k-8)x2-6x+k的顶点在x轴上,则k= .?
6.已知抛物线y=x2-5x-6与x轴交于A,B两点(点B在点A的右侧),与y轴交于点C,求△ABC的面积.
知识点 2 用图象法求一元二次方程的近似解
7.观察下表:
x
1.2
1.3
1.4
1.5
1.6
1.7
1.8
y=x2-
x-1
-0.76
-0.61
-0.44
-0.25
-0.04
0.19
0.44
结合表格,你认为一元二次方程x2-x-1=0的一个近似解是 ( )
A.x≈1.2 B.x≈1.4 C.x≈1.6 D.x≈1.8
8.利用函数图象求方程-x2+2x+2=0的实数根(精确到0.1),要先作函数 的图象,如图2所示,它与x轴的交点的横坐标大约是-0.7,2.7,所以方程-x2+2x+2=0的实数根约为x1= ,x2= .?
图2
知识点 3 二次函数与不等式
9.二次函数y=ax2+bx+c的图象如图3所示,则函数值y>0时,x的取值范围是 ( )
图3
A.x<-1 B.x>3 C.-1
10.如图4,若抛物线y1=-x2+2x+3与直线y2=ax+b(a≠0)相交于A(-12,m),B(2,n)两点,当y1>y2时,x的取值范围是 .?
图4
11.[教材习题21.3第9题变式] 已知函数y=x2-2x-3的图象如图5所示,利用图象法求不等式x2-2x-3<5的解集.
图5
12.[2020·毕节] 已知y=ax2+bx+c(a≠0)的图象如图6所示,对称轴为直线x=2.若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两个根,且x1
图6
A.x1+x2<0 B.4
13.[2019·合肥四十八中月考] 已知一次函数y1=kx+m和二次函数y2=ax2+bx+c部分的自变量与对应的函数值如下表:
x
…
-1
0
2
4
5
…
y1
…
0
1
3
5
6
…
y2
…
0
-1
0
5
9
…
当y2>y1时,自变量的取值范围是 ( )
A.-1
14.若将图7中的抛物线y=x2-2x+c向上平移,使它经过点(2,0),则此时的抛物线位于x轴下方的图象对应的x的取值范围是 .?
图7
15.若关于x的一元二次方程a(x+m)2-3=0的两个实数根分别为x1=-1,x2=3,则抛物线y=a(x+m-2)2-3与x轴的交点坐标为 .?
16.二次函数y=ax2+bx+c的图象如图8所示,根据图象解答下列问题:
(1)写出方程ax2+bx+c=0的两个根;
(2)写出不等式ax2+bx+c>0的解集;
(3)写出y随x的增大而减小时自变量x的取值范围;
(4)若方程ax2+bx+c=k有两个不相等的实数根,求k的取值范围.
图8
17.阅读下面的材料:
上课时李老师提出一个问题:对于任意实数x,关于x的不等式x2-2x-1-a>0恒成立,求a的取值范围.
小捷的思路是原不等式等价于x2-2x-1>a,设函数y1=x2-2x-1,y2=a,画出两个函数的图象的示意图,于是原问题转化为求函数y1的图象在y2的图象上方时a的取值范围.
(1)请结合小捷的思路回答:
对于任意实数x,关于x的不等式x2-2x-1-a>0恒成立,则a的取值范围是 ;?
(2)参考小捷思考问题的方法,解决问题:
关于x的方程x-4=a-3x在0
1.两 一 零
2.C [解析] 当x=0时,y=-x2+4x-4=-4,则抛物线与y轴的交点坐标为(0,-4).当y=0时,-x2+4x-4=0,解得x1=x2=2,抛物线与x轴的交点坐标为(2,0),所以抛物线与坐标轴有2个交点.故选C.
3.C [解析] 当k≠0时,抛物线与x轴有交点,则Δ=36-4k×3≥0,解得k≤3,且k≠0;当k=0时,一次函数y=-6x+3的图象与x轴有交点,因此k≤3.故选C.
4.x1=-1,x2=3 [解析] 由题意可知,抛物线与x轴的另一个交点坐标是(3,0),故该方程的两个解为x1=-1,x2=3.
5.9或-1 [解析] 抛物线的顶点在x轴上,则Δ=0,∴36-4k(k-8)=0,且k-8≠0,解得k1=9,k2=-1.故答案为9或-1.
6.[解析] 欲求△ABC的面积,必须先求出A,B,C三点的坐标.
解:令y=0,得一元二次方程x2-5x-6=0,解方程,得x1=6,x2=-1,
∴抛物线y=x2-5x-6与x轴的交点B,A的坐标分别为(6,0),(-1,0).
把x=0代入y=x2-5x-6,得y=-6,
∴点C的坐标为(0,-6).
∴S△ABC=12AB·OC=12×(6+1)×6=21.
7.C
8.y=-x2+2x+2 -0.7 2.7
9.D
10.-12
∴x1,x2是抛物线与x轴交点的横坐标.
∵抛物线的对称轴为直线x=2,
∴x1+x22=2,即x1+x2=4>0,故选项A错误;
∵x1
解得4
∴b2-4ac>0,故选项C错误;
∵抛物线开口向下,
∴a<0.
∵抛物线的对称轴为直线x=2,
∴-b2a=2,
∴b=-4a>0,
∴ab<0,故选项D错误.
故选B.
13.D [解析] ∵当x=-1时,y1=y2=0;当x=4时,y1=y2=5,∴直线与抛物线的交点为(-1,0)和(4,5),而-1
故选D.
14.0
16.解:(1)由图象可得,方程ax2+bx+c=0的两个根分别为x1=1,x2=3.
(2)由图象可知,当y=ax2+bx+c>0时,x的取值范围为1
(4)方程ax2+bx+c=k有两个不相等的实数根,实际上就是二次函数y=ax2+bx+c的图象与直线y=k有两个交点,由图象可知,此时k的取值范围是k<2.
17.解:(1)a<-2
(2)将原方程转化为x2-4x+3=a,设y1=x2-4x+3,y2=a,记函数y1在0
