第14章 全等三角形单元测试题 2021—2022学年沪科版八年级数学上册(word版含解析)
文档属性
| 名称 | 第14章 全等三角形单元测试题 2021—2022学年沪科版八年级数学上册(word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 215.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-29 00:00:00 | ||
图片预览



文档简介
第14章 全等三角形
一、选择题(每小题4分,共32分)
1.下列各组的两个图形属于全等图形的是( )
图1
2.如图2,AD,BC相交于点E.若△ABE≌△DCE,则下列结论中不正确的是( )
图2
A.AB=DC B.AB∥CD C.E为BC的中点 D.∠A=∠C
3.如图3,∠BDA=∠BDC,现添加以下哪个条件后,仍不能判定△ABD≌△CBD的是( )
图3
A.∠A=∠C B.∠ABD=∠CBD C.AB=CB D.AD=CD
4.下列条件中,不能作出唯一三角形的是( )
A.已知三角形两边的长度和两边夹角的度数
B.已知三角形两个角的度数以及两角夹边的长度
C.已知三角形两边的长度和其中一边的对角的度数
D.已知三角形三边的长度
5.有下列命题:(1)形状相同的两个三角形是全等三角形;(2)在两个三角形中,相等的角是对应角,相等的边是对应边;(3)全等三角形对应边上的高、中线及对应的角平分线分别相等.其中真命题有( )
A.3个 B.2个 C.1个 D.0个
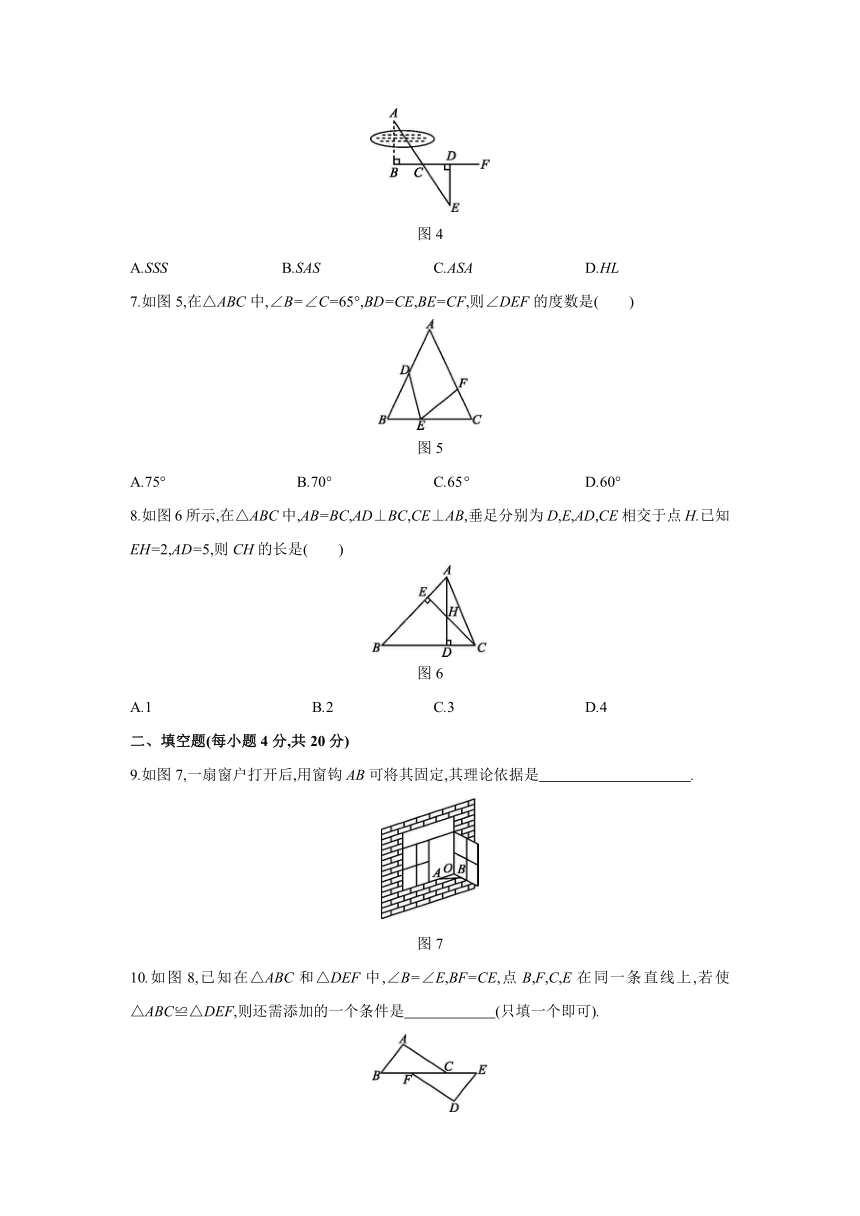
6.如图4,要在湖两岸A,B两点之间修建一座观赏桥,由于条件限制,无法直接测量A,B两点间的距离,于是小明想出来这样一种做法:在AB的垂线BF上取两点C,D,使BC=CD,再定出BF的垂线DE,使A,C,E三点在一条直线上,这时测得DE的长就是AB的长,依据是( )
图4
A.SSS B.SAS C.ASA D.HL
7.如图5,在△ABC中,∠B=∠C=65°,BD=CE,BE=CF,则∠DEF的度数是( )
图5
A.75° B.70° C.65 ° D.60°
8.如图6所示,在△ABC中,AB=BC,AD⊥BC,CE⊥AB,垂足分别为D,E,AD,CE相交于点H.已知EH=2,AD=5,则CH的长是( )
图6
A.1 B.2 C.3 D.4
二、填空题(每小题4分,共20分)
9.如图7,一扇窗户打开后,用窗钩AB可将其固定,其理论依据是 .?
图7
10.如图8,已知在△ABC和△DEF中,∠B=∠E,BF=CE,点B,F,C,E在同一条直线上,若使△ABC≌△DEF,则还需添加的一个条件是 (只填一个即可).?
图8
11.如图9,BD=CF,FD⊥BC于点D,DE⊥AB于点E,BE=CD,若∠AFD=140°,则∠EDF= °.?
图9
12.如图10,点A,D,C,B在同一条直线上,△ADF≌△BCE,DF与CE交于点M,∠B=32°,∠F=28°,则∠DMC的度数为 .?
图10
13.在△ABC中,AC=BC,l是过点C的直线,AD⊥l于点D,BE⊥l于点E,AD=CE.若AD=7,BE=2,则DE的长是 .?
三、解答题(共48分)
14.(14分)如图11,AD,BC相交于点O,AD=BC,∠C=∠D=90°.
(1)求证:△ACB≌△BDA;
(2)若∠ABC=36°,求∠CAO的度数.
图11
15.(16分)在数学课上,林老师在黑板上画出如图12所示的图形(其中点B,F,C,E在同一条直线上),并写出四个条件:①AB=DE;②BF=EC;③∠B=∠E;④∠1=∠2.
请你从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题,并给予证明.
题设: ;?
结论: .(均填写序号)?
证明:
图12
16.(18分)如图13,在△ABC和△EBD中,∠ABC=∠DBE=90°,AB=CB,BE=BD,连接AE,CD,AE与CD交于点M,AE与BC交于点N.
(1)求证:AE=CD.
(2)求证:AE⊥CD.
(3)连接BM,有以下两个结论:①BM平分∠CBE;②MB平分∠AMD.其中正确的是 .?
图13
答案
1.D [解析] 根据全等形是能够完全重合的两个图形进行分析判断:A项,两只眼睛下面的嘴巴不能完全重合,故本选项不符合题意.B项,两个正方形的边长不相等,不能完全重合,故本选项不符合题意.C项,圆内两条相交的线段不能完全重合,故本选项不符合题意.D项,两个图形能够完全重合,故本选项符合题意.
2.D [解析] ∵△ABE≌△DCE,
∴AB=CD,A选项说法正确,不符合题意;
∵△ABE≌△DCE,
∴∠A=∠D,
∴AB∥CD,B选项说法正确,不符合题意;
∵△ABE≌△DCE,
∴BE=EC,即E为BC的中点,C选项说法正确,不符合题意;
当△ABE≌△DCE时,∠A与∠C不一定相等,D选项说法错误,符合题意.
3.C [解析] ∵∠BDA=∠BDC,BD=BD,
∴当添加∠A=∠C时,可根据AAS判定△ABD≌△CBD;
当添加∠ABD=∠CBD时,可根据ASA判定△ABD≌△CBD;
当添加AD=CD时,可根据SAS判定△ABD≌△CBD;
当添加AB=CB时,不能判定△ABD≌△CBD.
4.C [解析] A项,根据SAS可得能作出唯一三角形;
B项,根据ASA可得能作出唯一三角形;
C项,根据条件不能作出唯一的三角形;
D项,根据SSS可得能作出唯一三角形.
故选C.
5.C
6.C [解析] 由题意可知∠ABC=∠EDC.
在△ABC和△EDC中,
∵∠ABC=∠EDC,BC=DC,∠ACB=∠ECD,
∴△ABC≌△EDC,(ASA)
∴DE=AB.
故选C.
7.C [解析] 在△DBE和△ECF中,
∵BD=CE,∠B=∠C,BE=CF,
∴△DBE≌△ECF.(SAS)
∴∠BDE=∠CEF.
∵∠BDE+∠BED=180°-65°=115°,
∴∠BED+∠CEF=115°.
∴∠DEF=180°-115°=65°.故选C.
8.C 9.三角形具有稳定性
10.答案不唯一,如:AB=DE
11.50 [解析] ∵∠AFD=140°,
∴∠DFC=40°.
∵DE⊥AB,DF⊥BC,
∴∠DEB=∠FDC=90°.
又∵BD=CF,BE=CD,
∴Rt△BDE≌Rt△CFD.(HL)
∴∠BDE=∠CFD=40°.
∴∠EDF=180°-∠FDC-∠BDE=50°.
故答案为50.
12.60° [解析] ∵△ADF≌△BCE,
∴∠A=∠B=32°,
∴∠MDC=∠A+∠F=32°+28°=60°.
同理可得∠MCD=60°,
∴∠DMC=180°-60°-60°=60°.
13.9或5 [解析] 有两种情况:
①如图(a),当点A,B位于直线l的同侧时,
∵AD⊥l,BE⊥l,
∴∠ADC=∠CEB=90°.
在Rt△ADC和Rt△CEB中,
∵AD=CE,AC=CB,
∴Rt△ADC≌Rt△CEB,
∴CE=AD=7,CD=BE=2,
∴DE=7+2=9.
②如图(b),当点A,B位于直线l的两侧时,
易证Rt△ADC≌Rt△CEB,
∴CE=AD=7,CD=BE=2,
∴DE=7-2=5.
综上,DE的长为9或5.
14.解:(1)证明:∵∠D=∠C=90°,
∴△ABC和△BAD都是直角三角形.
在Rt△ACB和Rt△BDA中,
∵BC=AD,AB=BA,
∴Rt△ACB≌Rt△BDA.(HL)
(2)∵Rt△ACB≌Rt△BDA,
∴∠ABC=∠BAD=36°.
又∵∠C=90°,
∴∠BAC=54°,
∴∠CAO=∠BAC-∠BAD=18°.
15.解:答案不唯一,如题设:①③④;结论:②.
证明:在△ABC和△DEF中,
∵∠1=∠2,∠B=∠E,AB=DE,
∴△ABC≌△DEF.
∴BC=EF.
∵BC=BF+CF,EF=EC+CF,
∴BF=EC.
16.解:(1)证明:∵∠ABC=∠DBE,
∴∠ABC+∠CBE=∠DBE+∠CBE,
即∠ABE=∠CBD.
在△ABE和△CBD中,∵AB=CB,∠ABE=∠CBD,BE=BD,
∴△ABE≌△CBD,∴AE=CD.
(2)证明:∵△ABE≌△CBD,
∴∠BAE=∠BCD.
∵∠NMC=180°-∠BCD-∠CNM,∠ABC=180°-∠BAE-∠ANB,∠CNM=∠ANB,∠ABC=90°,
∴∠NMC=90°,∴AE⊥CD.
(3)②
理由:如图,连接BM,作BK⊥AE于点K,BJ⊥CD于点J.
∵△ABE≌△CBD,
∴AE=CD,S△ABE=S△CBD,
∴12AE·BK=12CD·BJ,
∴BK=BJ.
在Rt△MBK和Rt△MBJ中,
∵BK=BJ,BM=BM,
∴Rt△MBK≌Rt△MBJ,
∴∠KMB=∠JMB,
即MB平分∠AMD,故②成立.
不妨设①成立,则△CBM≌△EBM,则BC=BE,故①错误.
故答案为②.
一、选择题(每小题4分,共32分)
1.下列各组的两个图形属于全等图形的是( )
图1
2.如图2,AD,BC相交于点E.若△ABE≌△DCE,则下列结论中不正确的是( )
图2
A.AB=DC B.AB∥CD C.E为BC的中点 D.∠A=∠C
3.如图3,∠BDA=∠BDC,现添加以下哪个条件后,仍不能判定△ABD≌△CBD的是( )
图3
A.∠A=∠C B.∠ABD=∠CBD C.AB=CB D.AD=CD
4.下列条件中,不能作出唯一三角形的是( )
A.已知三角形两边的长度和两边夹角的度数
B.已知三角形两个角的度数以及两角夹边的长度
C.已知三角形两边的长度和其中一边的对角的度数
D.已知三角形三边的长度
5.有下列命题:(1)形状相同的两个三角形是全等三角形;(2)在两个三角形中,相等的角是对应角,相等的边是对应边;(3)全等三角形对应边上的高、中线及对应的角平分线分别相等.其中真命题有( )
A.3个 B.2个 C.1个 D.0个
6.如图4,要在湖两岸A,B两点之间修建一座观赏桥,由于条件限制,无法直接测量A,B两点间的距离,于是小明想出来这样一种做法:在AB的垂线BF上取两点C,D,使BC=CD,再定出BF的垂线DE,使A,C,E三点在一条直线上,这时测得DE的长就是AB的长,依据是( )
图4
A.SSS B.SAS C.ASA D.HL
7.如图5,在△ABC中,∠B=∠C=65°,BD=CE,BE=CF,则∠DEF的度数是( )
图5
A.75° B.70° C.65 ° D.60°
8.如图6所示,在△ABC中,AB=BC,AD⊥BC,CE⊥AB,垂足分别为D,E,AD,CE相交于点H.已知EH=2,AD=5,则CH的长是( )
图6
A.1 B.2 C.3 D.4
二、填空题(每小题4分,共20分)
9.如图7,一扇窗户打开后,用窗钩AB可将其固定,其理论依据是 .?
图7
10.如图8,已知在△ABC和△DEF中,∠B=∠E,BF=CE,点B,F,C,E在同一条直线上,若使△ABC≌△DEF,则还需添加的一个条件是 (只填一个即可).?
图8
11.如图9,BD=CF,FD⊥BC于点D,DE⊥AB于点E,BE=CD,若∠AFD=140°,则∠EDF= °.?
图9
12.如图10,点A,D,C,B在同一条直线上,△ADF≌△BCE,DF与CE交于点M,∠B=32°,∠F=28°,则∠DMC的度数为 .?
图10
13.在△ABC中,AC=BC,l是过点C的直线,AD⊥l于点D,BE⊥l于点E,AD=CE.若AD=7,BE=2,则DE的长是 .?
三、解答题(共48分)
14.(14分)如图11,AD,BC相交于点O,AD=BC,∠C=∠D=90°.
(1)求证:△ACB≌△BDA;
(2)若∠ABC=36°,求∠CAO的度数.
图11
15.(16分)在数学课上,林老师在黑板上画出如图12所示的图形(其中点B,F,C,E在同一条直线上),并写出四个条件:①AB=DE;②BF=EC;③∠B=∠E;④∠1=∠2.
请你从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题,并给予证明.
题设: ;?
结论: .(均填写序号)?
证明:
图12
16.(18分)如图13,在△ABC和△EBD中,∠ABC=∠DBE=90°,AB=CB,BE=BD,连接AE,CD,AE与CD交于点M,AE与BC交于点N.
(1)求证:AE=CD.
(2)求证:AE⊥CD.
(3)连接BM,有以下两个结论:①BM平分∠CBE;②MB平分∠AMD.其中正确的是 .?
图13
答案
1.D [解析] 根据全等形是能够完全重合的两个图形进行分析判断:A项,两只眼睛下面的嘴巴不能完全重合,故本选项不符合题意.B项,两个正方形的边长不相等,不能完全重合,故本选项不符合题意.C项,圆内两条相交的线段不能完全重合,故本选项不符合题意.D项,两个图形能够完全重合,故本选项符合题意.
2.D [解析] ∵△ABE≌△DCE,
∴AB=CD,A选项说法正确,不符合题意;
∵△ABE≌△DCE,
∴∠A=∠D,
∴AB∥CD,B选项说法正确,不符合题意;
∵△ABE≌△DCE,
∴BE=EC,即E为BC的中点,C选项说法正确,不符合题意;
当△ABE≌△DCE时,∠A与∠C不一定相等,D选项说法错误,符合题意.
3.C [解析] ∵∠BDA=∠BDC,BD=BD,
∴当添加∠A=∠C时,可根据AAS判定△ABD≌△CBD;
当添加∠ABD=∠CBD时,可根据ASA判定△ABD≌△CBD;
当添加AD=CD时,可根据SAS判定△ABD≌△CBD;
当添加AB=CB时,不能判定△ABD≌△CBD.
4.C [解析] A项,根据SAS可得能作出唯一三角形;
B项,根据ASA可得能作出唯一三角形;
C项,根据条件不能作出唯一的三角形;
D项,根据SSS可得能作出唯一三角形.
故选C.
5.C
6.C [解析] 由题意可知∠ABC=∠EDC.
在△ABC和△EDC中,
∵∠ABC=∠EDC,BC=DC,∠ACB=∠ECD,
∴△ABC≌△EDC,(ASA)
∴DE=AB.
故选C.
7.C [解析] 在△DBE和△ECF中,
∵BD=CE,∠B=∠C,BE=CF,
∴△DBE≌△ECF.(SAS)
∴∠BDE=∠CEF.
∵∠BDE+∠BED=180°-65°=115°,
∴∠BED+∠CEF=115°.
∴∠DEF=180°-115°=65°.故选C.
8.C 9.三角形具有稳定性
10.答案不唯一,如:AB=DE
11.50 [解析] ∵∠AFD=140°,
∴∠DFC=40°.
∵DE⊥AB,DF⊥BC,
∴∠DEB=∠FDC=90°.
又∵BD=CF,BE=CD,
∴Rt△BDE≌Rt△CFD.(HL)
∴∠BDE=∠CFD=40°.
∴∠EDF=180°-∠FDC-∠BDE=50°.
故答案为50.
12.60° [解析] ∵△ADF≌△BCE,
∴∠A=∠B=32°,
∴∠MDC=∠A+∠F=32°+28°=60°.
同理可得∠MCD=60°,
∴∠DMC=180°-60°-60°=60°.
13.9或5 [解析] 有两种情况:
①如图(a),当点A,B位于直线l的同侧时,
∵AD⊥l,BE⊥l,
∴∠ADC=∠CEB=90°.
在Rt△ADC和Rt△CEB中,
∵AD=CE,AC=CB,
∴Rt△ADC≌Rt△CEB,
∴CE=AD=7,CD=BE=2,
∴DE=7+2=9.
②如图(b),当点A,B位于直线l的两侧时,
易证Rt△ADC≌Rt△CEB,
∴CE=AD=7,CD=BE=2,
∴DE=7-2=5.
综上,DE的长为9或5.
14.解:(1)证明:∵∠D=∠C=90°,
∴△ABC和△BAD都是直角三角形.
在Rt△ACB和Rt△BDA中,
∵BC=AD,AB=BA,
∴Rt△ACB≌Rt△BDA.(HL)
(2)∵Rt△ACB≌Rt△BDA,
∴∠ABC=∠BAD=36°.
又∵∠C=90°,
∴∠BAC=54°,
∴∠CAO=∠BAC-∠BAD=18°.
15.解:答案不唯一,如题设:①③④;结论:②.
证明:在△ABC和△DEF中,
∵∠1=∠2,∠B=∠E,AB=DE,
∴△ABC≌△DEF.
∴BC=EF.
∵BC=BF+CF,EF=EC+CF,
∴BF=EC.
16.解:(1)证明:∵∠ABC=∠DBE,
∴∠ABC+∠CBE=∠DBE+∠CBE,
即∠ABE=∠CBD.
在△ABE和△CBD中,∵AB=CB,∠ABE=∠CBD,BE=BD,
∴△ABE≌△CBD,∴AE=CD.
(2)证明:∵△ABE≌△CBD,
∴∠BAE=∠BCD.
∵∠NMC=180°-∠BCD-∠CNM,∠ABC=180°-∠BAE-∠ANB,∠CNM=∠ANB,∠ABC=90°,
∴∠NMC=90°,∴AE⊥CD.
(3)②
理由:如图,连接BM,作BK⊥AE于点K,BJ⊥CD于点J.
∵△ABE≌△CBD,
∴AE=CD,S△ABE=S△CBD,
∴12AE·BK=12CD·BJ,
∴BK=BJ.
在Rt△MBK和Rt△MBJ中,
∵BK=BJ,BM=BM,
∴Rt△MBK≌Rt△MBJ,
∴∠KMB=∠JMB,
即MB平分∠AMD,故②成立.
不妨设①成立,则△CBM≌△EBM,则BC=BE,故①错误.
故答案为②.
