第15章 轴对称图形与等腰三角形单元测试题 2021—2022学年沪科版八年级数学上册(word版含答案)
文档属性
| 名称 | 第15章 轴对称图形与等腰三角形单元测试题 2021—2022学年沪科版八年级数学上册(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 197.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-29 09:07:33 | ||
图片预览


文档简介
第15章 轴对称图形与等腰三角形
一、选择题(每小题4分,共32分)
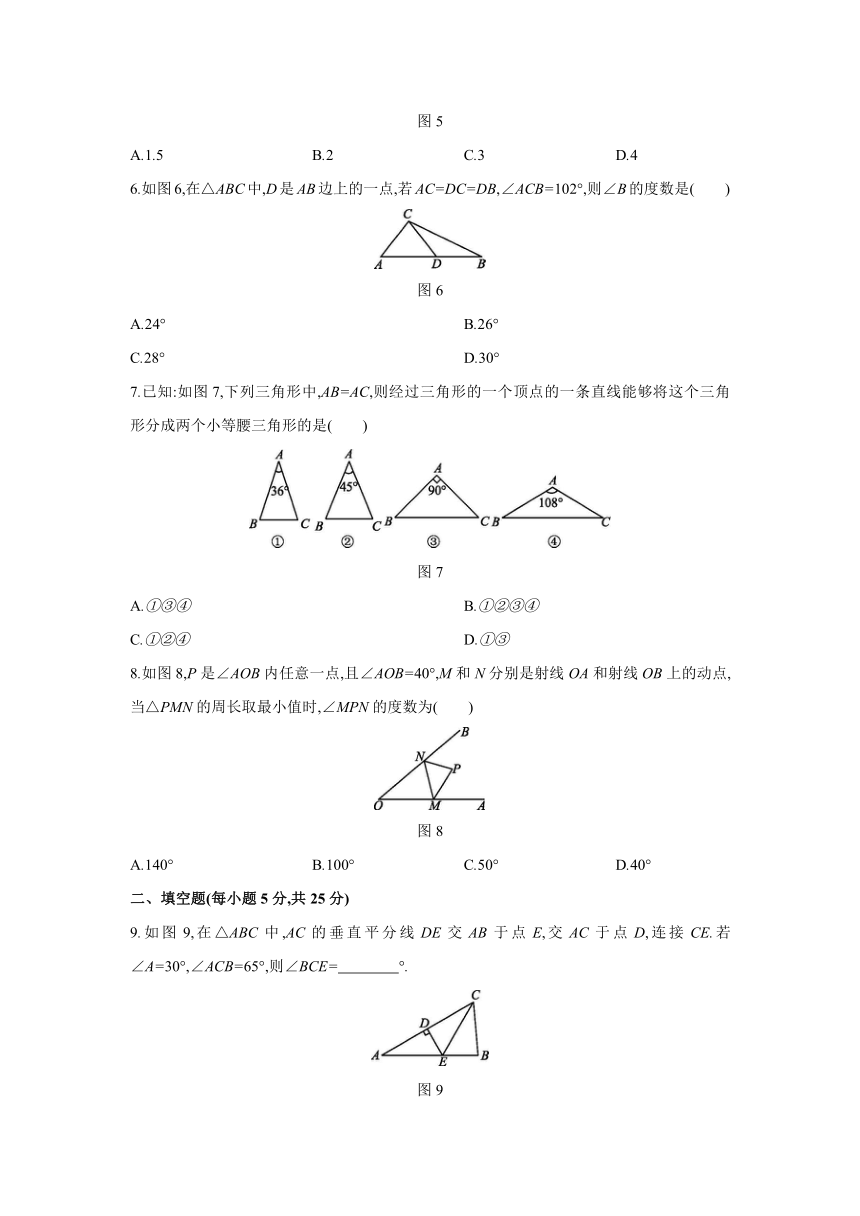
1.下列图形不是轴对称图形的是( )
图1
2.如图2,在△ABC中,DE垂直平分AC,若BC=22 cm,AB=14 cm,则△ABD的周长为( )
图2
A.24 cm B.25 cm
C.30 cm D.36 cm
3.已知点M(1-2m,m-1)关于x轴对称的点在第一象限,则m的取值范围在数轴上表示正确的是( )
图3
4.如图4所示,在等边三角形ABC中,AD⊥BC于点D,E为AD上一点,∠CED=50°,则∠ABE的度数为( )
图4
A.10° B.15°
C.20° D.25°
5.如图5,在△ABC中,D为AC上一点,∠C=90°,∠A=15°,∠DBC=60°,BC=1,则AD的长为( )
图5
A.1.5 B.2 C.3 D.4
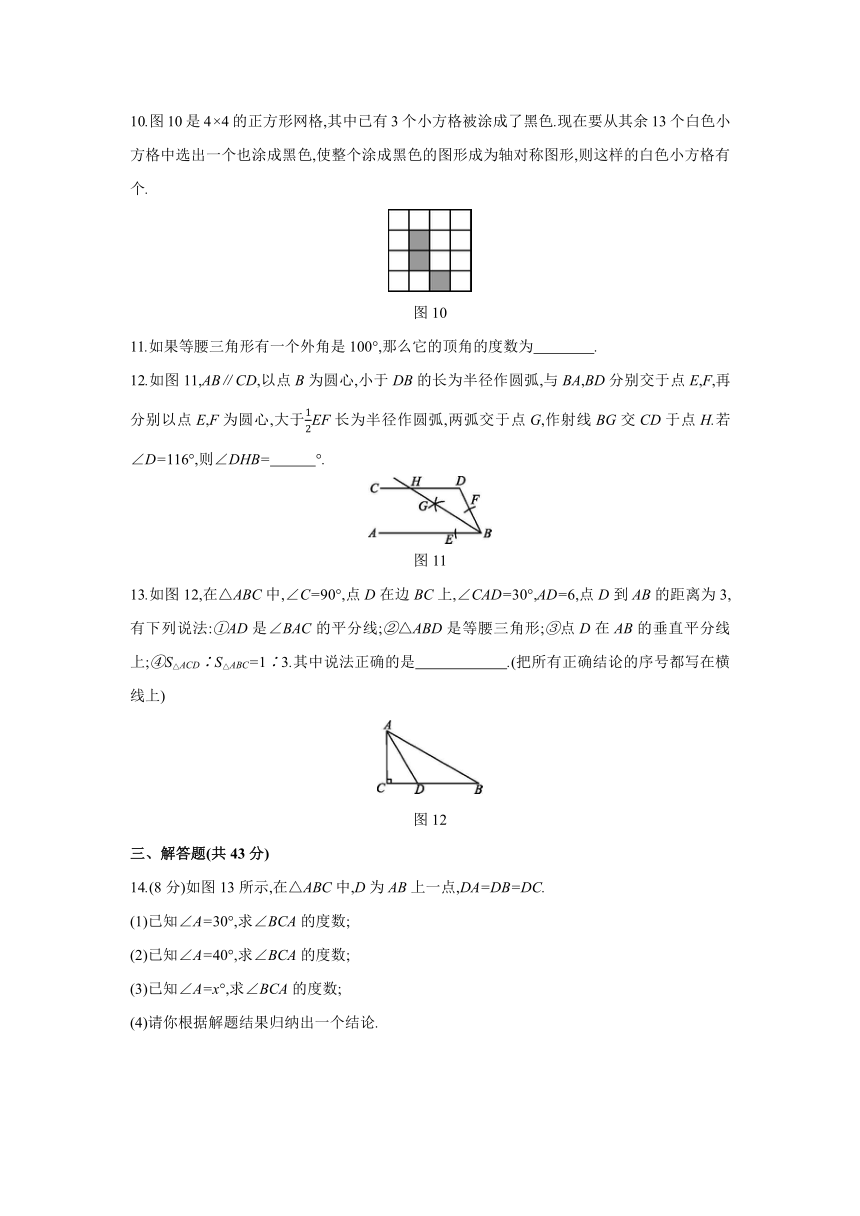
6.如图6,在△ABC中,D是AB边上的一点,若AC=DC=DB,∠ACB=102°,则∠B的度数是( )
图6
A.24° B.26°
C.28° D.30°
7.已知:如图7,下列三角形中,AB=AC,则经过三角形的一个顶点的一条直线能够将这个三角形分成两个小等腰三角形的是( )
图7
A.①③④ B.①②③④
C.①②④ D.①③
8.如图8,P是∠AOB内任意一点,且∠AOB=40°,M和N分别是射线OA和射线OB上的动点,当△PMN的周长取最小值时,∠MPN的度数为( )
图8
A.140° B.100° C.50° D.40°
二、填空题(每小题5分,共25分)
9.如图9,在△ABC中,AC的垂直平分线DE交AB于点E,交AC于点D,连接CE.若∠A=30°,∠ACB=65°,则∠BCE= °.?
图9
10.图10是4×4的正方形网格,其中已有3个小方格被涂成了黑色.现在要从其余13个白色小方格中选出一个也涂成黑色,使整个涂成黑色的图形成为轴对称图形,则这样的白色小方格有 个.?
图10
11.如果等腰三角形有一个外角是100°,那么它的顶角的度数为 .?
12.如图11,AB∥CD,以点B为圆心,小于DB的长为半径作圆弧,与BA,BD分别交于点E,F,再分别以点E,F为圆心,大于12EF长为半径作圆弧,两弧交于点G,作射线BG交CD于点H.若∠D=116°,则∠DHB= °.?
图11
13.如图12,在△ABC中,∠C=90°,点D在边BC上,∠CAD=30°,AD=6,点D到AB的距离为3,有下列说法:①AD是∠BAC的平分线;②△ABD是等腰三角形;③点D在AB的垂直平分线上;④S△ACD∶S△ABC=1∶3.其中说法正确的是 .(把所有正确结论的序号都写在横线上)?
图12
三、解答题(共43分)
14.(8分)如图13所示,在△ABC中,D为AB上一点,DA=DB=DC.
(1)已知∠A=30°,求∠BCA的度数;
(2)已知∠A=40°,求∠BCA的度数;
(3)已知∠A=x°,求∠BCA的度数;
(4)请你根据解题结果归纳出一个结论.
图13
15.(8分)如图14,P,Q是∠AOB内部的两个定点,M是∠AOB内部的一点,且点M到OA,OB的距离相等,到点P,点Q的距离也相等,请利用直尺和圆规作出点M.(不写作法,保留作图痕迹)
图14
16.(12分)已知:如图15,△ABC是等边三角形,D是AC边上一点,DE∥AB交BC于点E.
(1)求证:△CDE是等边三角形;
(2)连接BD,延长BC至点F,使得FD=BD,求证:AD=CF.
图15
17.(15分)如图16,O是等边三角形ABC内一点,∠AOC=100°,∠AOB=α.以OB为边作等边三角形BOD,连接CD.
(1)求证:△ABO≌△CBD;
(2)当α=150°时,试判断△COD的形状,并说明理由;
(3)探究:当α为多少度时,△COD是等腰三角形(直接写出结论)?
图16
答案
1.C
2.D [解析] ∵DE垂直平分AC,∴DA=DC,
∴△ABD的周长=AB+BD+DA=AB+BD+DC=AB+BC=14+22=36(cm).
故选D.
3.A [解析] 依题意,得1-2m>0,m-1<0,
即m<12,m<1.
∴m<12.
用数轴表示如选项A.
4.C [解析] ∵在等边三角形ABC中,AD⊥BC,
∴AD是BC的垂直平分线,且AD平分∠BAC.
∵E是AD上一点,∴EB=EC.
又∵AD⊥BC,∴∠BED=∠CED=50°.
又∵∠BAC=60°,AD平分∠BAC,
∴∠BAE=30°,
∴∠ABE=50°-30°=20°.
故选C.
5.B [解析] ∵∠DBC=60°,∠C=90°,
∴∠BDC=90°-60°=30°,
∴BD=2BC=2×1=2.
∵∠BDC=30°,∠A=15°,
∴∠ABD=∠BDC-∠A=15°,
∴∠ABD=∠A,
∴AD=BD=2.
故选B.
6.B [解析] 设∠B=x,∵AC=DC=DB,
∴∠CAD=∠CDA=2x,
∴∠ACB=180°-2x-x=102°,
解得x=26°,∴∠B=26°.故选B.
7.A
8.B
9.35
10.4 [解析] 如图所示,有4个位置可以使涂成黑色的图形成为轴对称图形.
11.20°或80°
12.32
13.①②③④ [解析] 过点D作DE⊥AB,垂足为E,则DE=3.在Rt△ACD中,∵∠CAD=30°,AD=6,∴CD=3,∠ADC=60°.∵DE=CD=3,DE⊥AB,DC⊥AC.∴AD是∠BAC的平分线.故①正确;
∴∠CAD=∠BAD=30°.又∵∠ADC=60°,∴∠B=30°=∠BAD.∴AD=BD=6.∴△ABD是等腰三角形.故②正确;∵DA=DB,DE⊥AB,∴DE是AB的垂直平分线.∴点D在AB的垂直平分线上.故③正确;∵CB=CD+DB=3+6=9,∴S△ACD∶S△ABC=CD∶BC=3∶9=1∶3.故④正确.故答案为①②③④.
14.解:(1)∠BCA=90°.
(2)∠BCA=90°.
(3)∠BCA=90°.
(4)若三角形一边上的中线等于该边的一半,则这个三角形是直角三角形,且该边为斜边.
15.解:如图,点M即为所求.
16.证明:(1)∵△ABC是等边三角形,
∴∠A=∠ABC=∠ACB=60°.
∵DE∥AB,
∴∠CDE=∠A,∠CED=∠ABC,
∴∠ACB=∠CDE=∠CED=60°,
故△CDE是等边三角形.
(2)∵△CDE是等边三角形,
∴DC=DE.
∵DB=DF,
∴∠DBC=∠DFE.
在△DBC和△DFE中,
∵∠DBC=∠DFE,∠DCB=∠DEF,DC=DE,
∴△DBC≌△DFE(AAS),
∴BC=FE,
∴BC-EC=FE-EC,
即BE=CF.
又∵BC=CA,CE=CD,
∴BE=AD,
∴AD=CF.
17.解:(1)证明:∵△ABC和△BOD都是等边三角形,
∴BA=BC,BO=BD,∠ABC=∠OBD=60°.
∴∠ABC-∠OBC=∠OBD-∠OBC,
即∠ABO=∠CBD.
在△ABO和△CBD中,
∵BA=BC,∠ABO=∠CBD,BO=BD,
∴△ABO≌△CBD(SAS).
(2)△COD是直角三角形.
理由:∵△ABO≌△CBD,
∴∠BDC=∠BOA=150°.
又∵∠ODB=∠BOD=60°,
∴∠CDO=150°-60°=90°,∠COD=360°-100°-150°-60°=50°.
∴△COD是直角三角形.
(3)易得∠ODC=∠BDC-∠BDO=α-60°,
∠DOC=360°-∠AOC-∠AOB-∠BOD=200°-α,
∴∠OCD=180°-∠ODC-∠DOC=180°-(α-60°)-(200°-α)=40°.
①若OC=CD,则∠DOC=∠ODC,
∴200°-α=α-60°.
∴α=130°;
②若OC=OD,则∠OCD=∠ODC,
∴40°=α-60°.
∴α=100°;
③若OD=CD,则∠DOC=∠OCD,
∴200°-α=40°.
∴α=160°.
综上所述,当α为100°,130°,160°时,△COD是等腰三角形.
一、选择题(每小题4分,共32分)
1.下列图形不是轴对称图形的是( )
图1
2.如图2,在△ABC中,DE垂直平分AC,若BC=22 cm,AB=14 cm,则△ABD的周长为( )
图2
A.24 cm B.25 cm
C.30 cm D.36 cm
3.已知点M(1-2m,m-1)关于x轴对称的点在第一象限,则m的取值范围在数轴上表示正确的是( )
图3
4.如图4所示,在等边三角形ABC中,AD⊥BC于点D,E为AD上一点,∠CED=50°,则∠ABE的度数为( )
图4
A.10° B.15°
C.20° D.25°
5.如图5,在△ABC中,D为AC上一点,∠C=90°,∠A=15°,∠DBC=60°,BC=1,则AD的长为( )
图5
A.1.5 B.2 C.3 D.4
6.如图6,在△ABC中,D是AB边上的一点,若AC=DC=DB,∠ACB=102°,则∠B的度数是( )
图6
A.24° B.26°
C.28° D.30°
7.已知:如图7,下列三角形中,AB=AC,则经过三角形的一个顶点的一条直线能够将这个三角形分成两个小等腰三角形的是( )
图7
A.①③④ B.①②③④
C.①②④ D.①③
8.如图8,P是∠AOB内任意一点,且∠AOB=40°,M和N分别是射线OA和射线OB上的动点,当△PMN的周长取最小值时,∠MPN的度数为( )
图8
A.140° B.100° C.50° D.40°
二、填空题(每小题5分,共25分)
9.如图9,在△ABC中,AC的垂直平分线DE交AB于点E,交AC于点D,连接CE.若∠A=30°,∠ACB=65°,则∠BCE= °.?
图9
10.图10是4×4的正方形网格,其中已有3个小方格被涂成了黑色.现在要从其余13个白色小方格中选出一个也涂成黑色,使整个涂成黑色的图形成为轴对称图形,则这样的白色小方格有 个.?
图10
11.如果等腰三角形有一个外角是100°,那么它的顶角的度数为 .?
12.如图11,AB∥CD,以点B为圆心,小于DB的长为半径作圆弧,与BA,BD分别交于点E,F,再分别以点E,F为圆心,大于12EF长为半径作圆弧,两弧交于点G,作射线BG交CD于点H.若∠D=116°,则∠DHB= °.?
图11
13.如图12,在△ABC中,∠C=90°,点D在边BC上,∠CAD=30°,AD=6,点D到AB的距离为3,有下列说法:①AD是∠BAC的平分线;②△ABD是等腰三角形;③点D在AB的垂直平分线上;④S△ACD∶S△ABC=1∶3.其中说法正确的是 .(把所有正确结论的序号都写在横线上)?
图12
三、解答题(共43分)
14.(8分)如图13所示,在△ABC中,D为AB上一点,DA=DB=DC.
(1)已知∠A=30°,求∠BCA的度数;
(2)已知∠A=40°,求∠BCA的度数;
(3)已知∠A=x°,求∠BCA的度数;
(4)请你根据解题结果归纳出一个结论.
图13
15.(8分)如图14,P,Q是∠AOB内部的两个定点,M是∠AOB内部的一点,且点M到OA,OB的距离相等,到点P,点Q的距离也相等,请利用直尺和圆规作出点M.(不写作法,保留作图痕迹)
图14
16.(12分)已知:如图15,△ABC是等边三角形,D是AC边上一点,DE∥AB交BC于点E.
(1)求证:△CDE是等边三角形;
(2)连接BD,延长BC至点F,使得FD=BD,求证:AD=CF.
图15
17.(15分)如图16,O是等边三角形ABC内一点,∠AOC=100°,∠AOB=α.以OB为边作等边三角形BOD,连接CD.
(1)求证:△ABO≌△CBD;
(2)当α=150°时,试判断△COD的形状,并说明理由;
(3)探究:当α为多少度时,△COD是等腰三角形(直接写出结论)?
图16
答案
1.C
2.D [解析] ∵DE垂直平分AC,∴DA=DC,
∴△ABD的周长=AB+BD+DA=AB+BD+DC=AB+BC=14+22=36(cm).
故选D.
3.A [解析] 依题意,得1-2m>0,m-1<0,
即m<12,m<1.
∴m<12.
用数轴表示如选项A.
4.C [解析] ∵在等边三角形ABC中,AD⊥BC,
∴AD是BC的垂直平分线,且AD平分∠BAC.
∵E是AD上一点,∴EB=EC.
又∵AD⊥BC,∴∠BED=∠CED=50°.
又∵∠BAC=60°,AD平分∠BAC,
∴∠BAE=30°,
∴∠ABE=50°-30°=20°.
故选C.
5.B [解析] ∵∠DBC=60°,∠C=90°,
∴∠BDC=90°-60°=30°,
∴BD=2BC=2×1=2.
∵∠BDC=30°,∠A=15°,
∴∠ABD=∠BDC-∠A=15°,
∴∠ABD=∠A,
∴AD=BD=2.
故选B.
6.B [解析] 设∠B=x,∵AC=DC=DB,
∴∠CAD=∠CDA=2x,
∴∠ACB=180°-2x-x=102°,
解得x=26°,∴∠B=26°.故选B.
7.A
8.B
9.35
10.4 [解析] 如图所示,有4个位置可以使涂成黑色的图形成为轴对称图形.
11.20°或80°
12.32
13.①②③④ [解析] 过点D作DE⊥AB,垂足为E,则DE=3.在Rt△ACD中,∵∠CAD=30°,AD=6,∴CD=3,∠ADC=60°.∵DE=CD=3,DE⊥AB,DC⊥AC.∴AD是∠BAC的平分线.故①正确;
∴∠CAD=∠BAD=30°.又∵∠ADC=60°,∴∠B=30°=∠BAD.∴AD=BD=6.∴△ABD是等腰三角形.故②正确;∵DA=DB,DE⊥AB,∴DE是AB的垂直平分线.∴点D在AB的垂直平分线上.故③正确;∵CB=CD+DB=3+6=9,∴S△ACD∶S△ABC=CD∶BC=3∶9=1∶3.故④正确.故答案为①②③④.
14.解:(1)∠BCA=90°.
(2)∠BCA=90°.
(3)∠BCA=90°.
(4)若三角形一边上的中线等于该边的一半,则这个三角形是直角三角形,且该边为斜边.
15.解:如图,点M即为所求.
16.证明:(1)∵△ABC是等边三角形,
∴∠A=∠ABC=∠ACB=60°.
∵DE∥AB,
∴∠CDE=∠A,∠CED=∠ABC,
∴∠ACB=∠CDE=∠CED=60°,
故△CDE是等边三角形.
(2)∵△CDE是等边三角形,
∴DC=DE.
∵DB=DF,
∴∠DBC=∠DFE.
在△DBC和△DFE中,
∵∠DBC=∠DFE,∠DCB=∠DEF,DC=DE,
∴△DBC≌△DFE(AAS),
∴BC=FE,
∴BC-EC=FE-EC,
即BE=CF.
又∵BC=CA,CE=CD,
∴BE=AD,
∴AD=CF.
17.解:(1)证明:∵△ABC和△BOD都是等边三角形,
∴BA=BC,BO=BD,∠ABC=∠OBD=60°.
∴∠ABC-∠OBC=∠OBD-∠OBC,
即∠ABO=∠CBD.
在△ABO和△CBD中,
∵BA=BC,∠ABO=∠CBD,BO=BD,
∴△ABO≌△CBD(SAS).
(2)△COD是直角三角形.
理由:∵△ABO≌△CBD,
∴∠BDC=∠BOA=150°.
又∵∠ODB=∠BOD=60°,
∴∠CDO=150°-60°=90°,∠COD=360°-100°-150°-60°=50°.
∴△COD是直角三角形.
(3)易得∠ODC=∠BDC-∠BDO=α-60°,
∠DOC=360°-∠AOC-∠AOB-∠BOD=200°-α,
∴∠OCD=180°-∠ODC-∠DOC=180°-(α-60°)-(200°-α)=40°.
①若OC=CD,则∠DOC=∠ODC,
∴200°-α=α-60°.
∴α=130°;
②若OC=OD,则∠OCD=∠ODC,
∴40°=α-60°.
∴α=100°;
③若OD=CD,则∠DOC=∠OCD,
∴200°-α=40°.
∴α=160°.
综上所述,当α为100°,130°,160°时,△COD是等腰三角形.
