人教版七年级数学上册试题 一课一练 4.1 《 几何图形》习题1(word版含答案)
文档属性
| 名称 | 人教版七年级数学上册试题 一课一练 4.1 《 几何图形》习题1(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 321.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-29 00:00:00 | ||
图片预览



文档简介
4.1
《
几何图形》习题1
一、选择题
1.下列各组图形中都是平面图形的是( )
A.三角形、圆、球、圆锥
B.点、线段、棱锥、棱柱
C.角、三角形、正方形、圆
D.点、角、线段、长方体
2.下列几何体中,属于柱体的有(
)
A.1个
B.2个
C.3个
D.4个
3.一个长方体每个角都被割去(相邻两个角之间还有一段原来的棱),得到的几何体有()条棱.
A.24
B.30
C.36
D.42
4.水平地面上的球和圆柱体如图摆放,其主视图是(
)
A.
B.
C.
D.
5.现在社会快递业发展迅速,各种精美安全的包装也深受大家的喜欢,下图是某快递公司使用的包装
盒平面图,能够折叠呈长方体纸盒的是(
)
A.①②
B.①③
C.②③
D.③④
6.某几何体的三视图如图所示,则下列说法错误的是(
)
A.该几何体是长方体
B.该几何体的高是3
C.底面有一边的长是1
D.该几何体的表面积为18平方单位
7.如图,某同学在制作正方体模型的时候,在方格纸上画出几个小正方形(图中阴影部分),但是由于疏忽少画了一个,请你给他补上一个,使之可以组合成正方体,你一共有(
)种画法.
A.2
B.3
C.4
D.5
8.如图,下列图形绕直线旋转一周后,能得到圆锥体的是(
)
A.
B.
C.
D.
9.用一个平面去截正方体,截面的形状不可能是( )
A.四边形
B.五边形
C.六边形
D.七边形
10.如图是一个正方体纸盒的表面展开图,若在其中三个正方形A、B、C内分别填入适当的数,使它折成正方体后相对的面上的两数互为相反数,则填在正方形A、B、C内的三个数依次为(
)
A.-2,1,0
B.1,-2,0
C.0,-2,1
D.-2,0,1
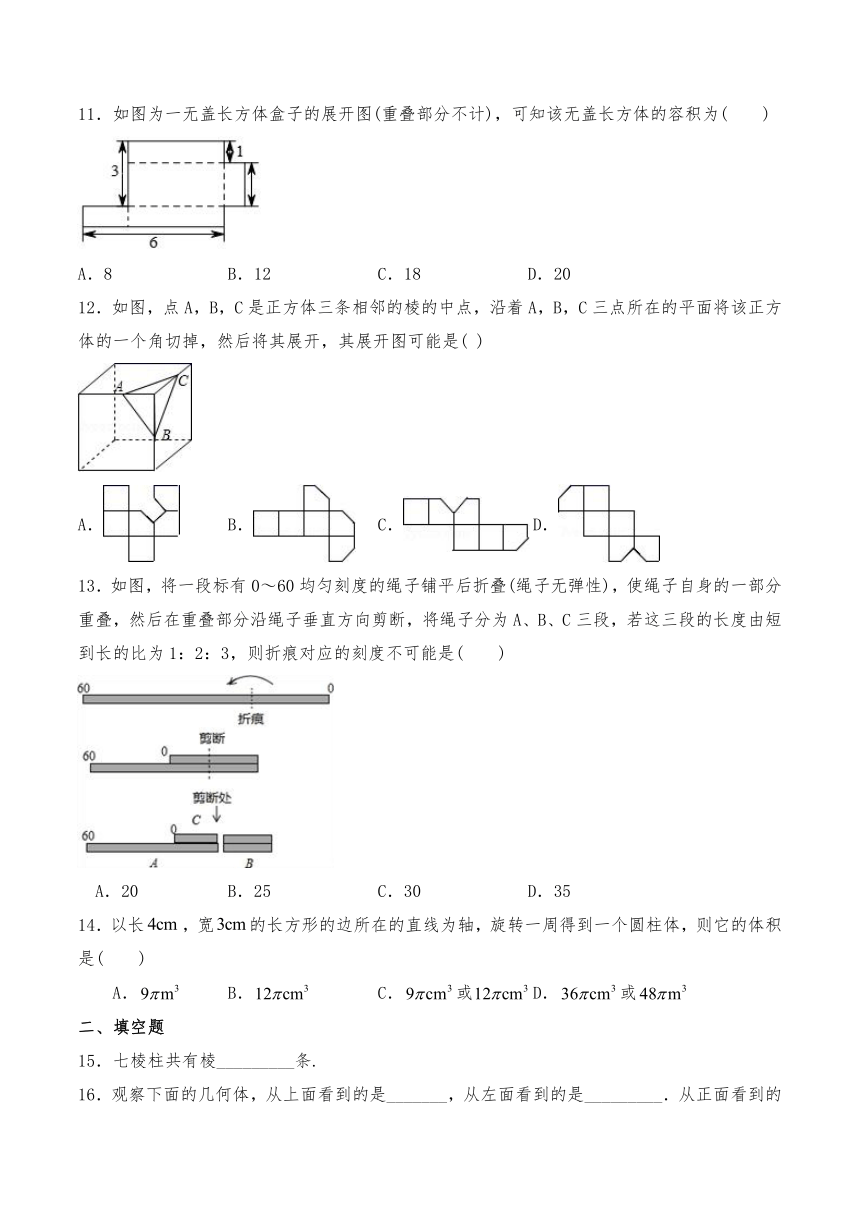
11.如图为一无盖长方体盒子的展开图(重叠部分不计),可知该无盖长方体的容积为( )
A.8
B.12
C.18
D.20
12.如图,点A,B,C是正方体三条相邻的棱的中点,沿着A,B,C三点所在的平面将该正方体的一个角切掉,然后将其展开,其展开图可能是(
)
A.
B.
C.
D.
13.如图,将一段标有0~60均匀刻度的绳子铺平后折叠(绳子无弹性),使绳子自身的一部分重叠,然后在重叠部分沿绳子垂直方向剪断,将绳子分为A、B、C三段,若这三段的长度由短到长的比为1:2:3,则折痕对应的刻度不可能是( )
A.20
B.25
C.30
D.35
14.以长,宽的长方形的边所在的直线为轴,旋转一周得到一个圆柱体,则它的体积是(
)
A.
B.
C.或
D.或
二、填空题
15.七棱柱共有棱_________条.
16.观察下面的几何体,从上面看到的是_______,从左面看到的是_________.从正面看到的是________.
17.在图中增加1个小正方形,使所得图形经过折叠能够围成一个正方体,在图中适合按要求加上小正方形的位置有_________个.
18.把小正方体的6个面分别涂上六种不同的颜色,并画上朵数不等的花,各面上的颜色和花的朵数情况如表:现将上述大小相等、颜色花朵分布完全一样的四个立方体拼成一个水平放置的长方体(如图),那么长方体下底面有________朵花.
三、解答题
19.下面是从不同方向观察某一个用小方块搭的立体图形时,看到的两个平面图形,判断两位同学用小方块搭的立体图形是否正确.
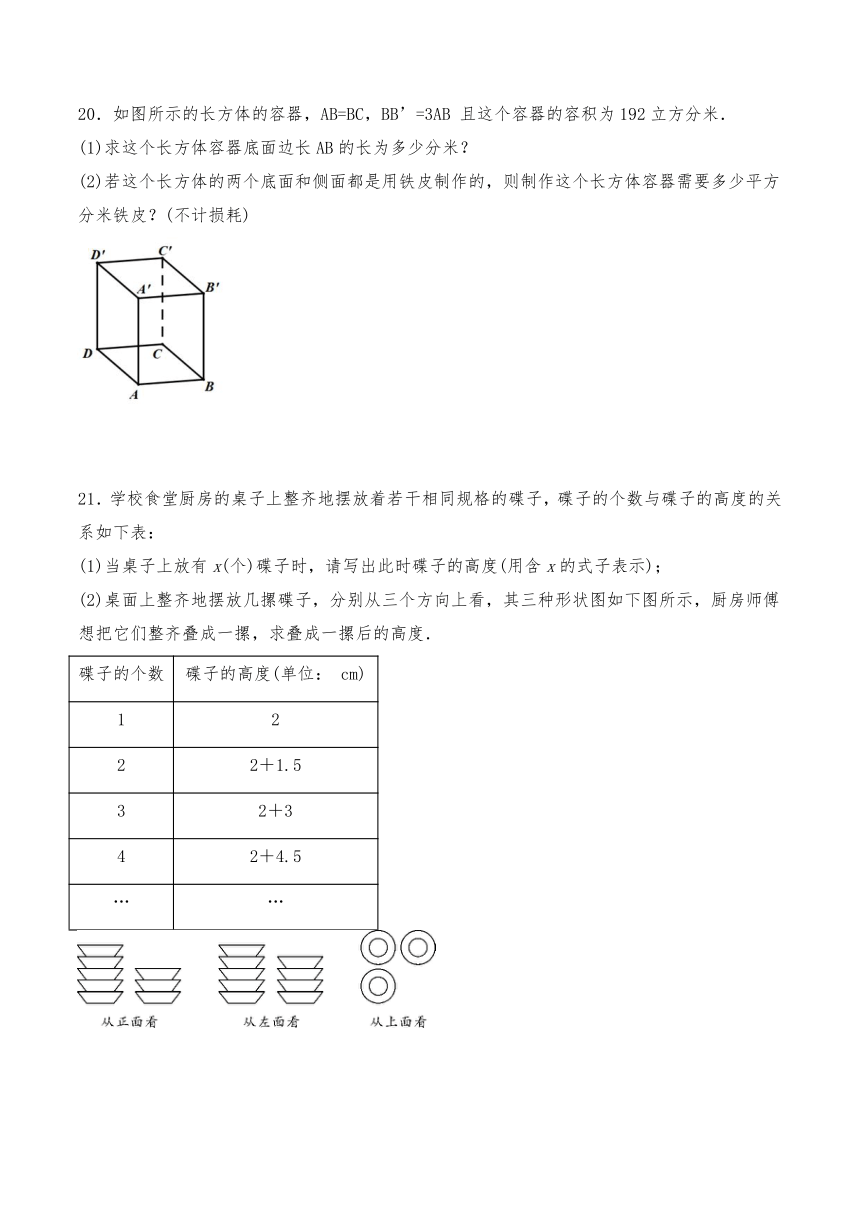
20.如图所示的长方体的容器,AB=BC,BB’=3AB
且这个容器的容积为192立方分米.
(1)求这个长方体容器底面边长AB的长为多少分米?
(2)若这个长方体的两个底面和侧面都是用铁皮制作的,则制作这个长方体容器需要多少平方分米铁皮?(不计损耗)
21.学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:
(1)当桌子上放有x(个)碟子时,请写出此时碟子的高度(用含x的式子表示);
(2)桌面上整齐地摆放几摞碟子,分别从三个方向上看,其三种形状图如下图所示,厨房师傅想把它们整齐叠成一摞,求叠成一摞后的高度.
碟子的个数
碟子的高度(单位:
cm)
1
2
2
2+1.5
3
2+3
4
2+4.5
…
…
22.将立方体纸盒沿某些棱剪开,且使六个面连在一起,然后铺平,可以得到其表面展开图的平面图形.
(1)以下两个方格图中的阴影部分能表示立方体表面展开图的是
(填A或B).
(2)在以下方格图中,画一个与(1)中呈现的阴影部分不相似(包括不全等)的立方体表面展开图.(用阴影表示)
(3)如图中的实线是立方体纸盒的剪裁线,请将其表面展开图画在右图的方格图中.(用阴影表示)
23.把棱长为1cm的若干个小正方体摆放成如图所示的几何体,然后在露出的表面上涂上颜色(不含底面)
(1)该几何体中有
小正方体?
(2)其中两面被涂到的有
个小正方体;没被涂到的有
个小正方体;
(3)求出涂上颜色部分的总面积.
24.如图是一张长方形纸片,长为,长为.
(1)若将此长方形纸片绕它的一边所在直线旋转一周,则形成的几何体是______;
(2)若将这个长方形纸片绕边所在直线旋转一周,则形成的几何体的体积是____(结果保留);
(3)若将这个长方形纸片绕它的一边所在直线旋转一周,求形成的几何体的表面积(结果保留).
25.十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在一个有趣的关系式,这个关系式被称为欧拉公式.请你观察下列几种简单的多面体模型,解答下列问题:
(1)完成表格:
多面体
顶点数(V)
面数(F)
棱数(E)
四面体
4
4
6
长方体
8
6
12
八面体
6
8
12
某多面体
20
30
你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是
F=
;(用
含
V、E
的式子表示)
(2)如果一个多面体每个顶点处都有a条棱,那么这个多面体的棱数(E)与顶点数(V)之间的关系式为
E=
a×V
.现有一个二十面体,有12个顶点,每个顶点处有
5
条棱,那么该二十面体有多少条棱?
(3)某个玻璃饰品的外形是简单多面体,它的外表面是由三角形和六边形两种多边形用含
n
的代数式表示)拼接而成,且有
18个顶点,每个顶点处都有4
条棱,设该多面体表面三角形的个数为
m,六边形的个数为
n,求m+n
的值.
26.如图所示,在一张正方形纸片的四个角上各剪去一个同样大小的正方形,然后把剩下的部分折成一个无盖的长方体盒子.请回答下列问题:
(1)剪去的小正方形的边长与折成的无盖长方体盒子的高之间的大小关系为
;
(2)如果设原来这张正方形纸片的边长为,所折成的无盖长方体盒子的高为,那么,这个无盖长方体盒子的容积可以表示为
;
(3)如果原正方形纸片的边长为,剪去的小正方形的边长按整数值依次变化,即分别取
时,计算折成
的无盖长方体盒子的容积得到下表,由此可以判断,当剪去的小正方形边长为
时,折成的无盖长方体盒子的容积最大
剪去的小正方
形的边长
1
2
3
4
5
6
7
8
9
10
折成的无盖长方体的容积
324
576
500
384
252
128
36
0
答案
一、选择题
1.C
2.B.
3.C
4.B.
5.A.
6.D
7.B
8.B.
9.D.
10.C
11.A.
12.D.
13.C
14.D.
二、填空题
15.21
16.③
②
①
17.4
18.17
三、解答题
19.观察图形可知,张度搭成的图形从正面看到的图形是,符合题意;
从上面看到的图形是,符合题意,
∴张度搭成的立体图形是正确的;
李磊搭成的图形从正面看到的图形是,符合题意;
从上面看到的图形是,不符合题意,
∴李磊搭成的立体图形是错误的.
20.解:(1)设
AB=BC,BB’=3AB,
由这个容器的容积为192立方分米,
(分米).
(2)
长方体的表面积为:
(平方分米),
制作这个长方体容器需要平方分米的铁皮.
21.(1)由图可知,每增加一个碟子高度增加1.5cm,桌子上放有x个碟子时,高度为2+1.5(x?1)=1.5x+0.5;
(2)由图可知,共有3摞,左前一摞有5个,左后一摞有4个,右边前面一摞有3个,
共有:3+4+5=12个,叠成一摞后的高度=1.5×12+0.5=18.5cm.
答:叠成一摞后的高度为18.5
cm.
22.解:(1)两个方格图中的阴影部分能表示立方体表面展开图的是A,
故答案为:A.
(2)立方体表面展开图如图所示:
(3)将其表面展开图画在方格图中如图所示:
23.(1)该几何体中正方体的个数为9+4+1=14个;
(2)根据图中小正方体的位置可知:最底层外边中间的小正方体被涂到2个面,共4个,只有最底层正中间的小正方体没被涂到,
故答案为4;1;
(3)先算侧面--底层12个小面;
中层8个小面;
上层4个小面;
再算上面--上层1个
中层3个(正方体是可以移动的,不管放在哪里,它压住的面积总是它的底面积,也就是一个,所以中层是4减1个)底层(9-4)=5个,
∴总共12+8+4+1+3+5=33个小面.
∴涂上颜色部分的总面积=1133=33cm2.
24.(1)圆柱;
(2)
绕AB旋转得到的圆柱的底面半径为,高为,体积;
(3)绕边所在直线旋转得到的圆柱的底面半径为,高为,
表面积是:;
绕边所在直线旋转得到的圆柱的底面半径为,高为,
表面积是:.
答:形成的几何体的表面积是或.
25.解:(1)
多面体
顶点数()
面数()
棱数()
四面体
4
4
6
长方体
8
6
12
正八面体
6
8
12
正十二面体
20
12
30
(2)∵(条)
∴该二十面体共有30条棱.
(3))∵有18个顶点,每个顶点处都有4条棱,两点确定一条直线;
∴共有18×4÷2=36(条棱),
∵F=E?V+2
∴18+F-36=2,
解得:F=20,
∴m+n=20;
26.解:(1)由折叠可知,
剪去的小正方形的边长与折成的无盖长方体盒子的高之间的大小关系为相等,
故答案为:相等;
(2)这个无盖长方体盒子的容积=h(a-2h)(a-2h)=h(a-2h)2(cm3);
故答案为:h(a-2h)2;
(3)当剪去的小正方形的边长取2时,m=2×(20-2×2)2=512,
当剪去的小正方形的边长取3时,n=3×(20-2×3)2=588,
当剪去的小正方形的边长的值逐渐增大时,所得到的无盖长方体纸盒的容积的值先增大后减小,
当剪去的小正方形的边长为3cm时,所得到的无盖长方体纸盒的容积最大.
《
几何图形》习题1
一、选择题
1.下列各组图形中都是平面图形的是( )
A.三角形、圆、球、圆锥
B.点、线段、棱锥、棱柱
C.角、三角形、正方形、圆
D.点、角、线段、长方体
2.下列几何体中,属于柱体的有(
)
A.1个
B.2个
C.3个
D.4个
3.一个长方体每个角都被割去(相邻两个角之间还有一段原来的棱),得到的几何体有()条棱.
A.24
B.30
C.36
D.42
4.水平地面上的球和圆柱体如图摆放,其主视图是(
)
A.
B.
C.
D.
5.现在社会快递业发展迅速,各种精美安全的包装也深受大家的喜欢,下图是某快递公司使用的包装
盒平面图,能够折叠呈长方体纸盒的是(
)
A.①②
B.①③
C.②③
D.③④
6.某几何体的三视图如图所示,则下列说法错误的是(
)
A.该几何体是长方体
B.该几何体的高是3
C.底面有一边的长是1
D.该几何体的表面积为18平方单位
7.如图,某同学在制作正方体模型的时候,在方格纸上画出几个小正方形(图中阴影部分),但是由于疏忽少画了一个,请你给他补上一个,使之可以组合成正方体,你一共有(
)种画法.
A.2
B.3
C.4
D.5
8.如图,下列图形绕直线旋转一周后,能得到圆锥体的是(
)
A.
B.
C.
D.
9.用一个平面去截正方体,截面的形状不可能是( )
A.四边形
B.五边形
C.六边形
D.七边形
10.如图是一个正方体纸盒的表面展开图,若在其中三个正方形A、B、C内分别填入适当的数,使它折成正方体后相对的面上的两数互为相反数,则填在正方形A、B、C内的三个数依次为(
)
A.-2,1,0
B.1,-2,0
C.0,-2,1
D.-2,0,1
11.如图为一无盖长方体盒子的展开图(重叠部分不计),可知该无盖长方体的容积为( )
A.8
B.12
C.18
D.20
12.如图,点A,B,C是正方体三条相邻的棱的中点,沿着A,B,C三点所在的平面将该正方体的一个角切掉,然后将其展开,其展开图可能是(
)
A.
B.
C.
D.
13.如图,将一段标有0~60均匀刻度的绳子铺平后折叠(绳子无弹性),使绳子自身的一部分重叠,然后在重叠部分沿绳子垂直方向剪断,将绳子分为A、B、C三段,若这三段的长度由短到长的比为1:2:3,则折痕对应的刻度不可能是( )
A.20
B.25
C.30
D.35
14.以长,宽的长方形的边所在的直线为轴,旋转一周得到一个圆柱体,则它的体积是(
)
A.
B.
C.或
D.或
二、填空题
15.七棱柱共有棱_________条.
16.观察下面的几何体,从上面看到的是_______,从左面看到的是_________.从正面看到的是________.
17.在图中增加1个小正方形,使所得图形经过折叠能够围成一个正方体,在图中适合按要求加上小正方形的位置有_________个.
18.把小正方体的6个面分别涂上六种不同的颜色,并画上朵数不等的花,各面上的颜色和花的朵数情况如表:现将上述大小相等、颜色花朵分布完全一样的四个立方体拼成一个水平放置的长方体(如图),那么长方体下底面有________朵花.
三、解答题
19.下面是从不同方向观察某一个用小方块搭的立体图形时,看到的两个平面图形,判断两位同学用小方块搭的立体图形是否正确.
20.如图所示的长方体的容器,AB=BC,BB’=3AB
且这个容器的容积为192立方分米.
(1)求这个长方体容器底面边长AB的长为多少分米?
(2)若这个长方体的两个底面和侧面都是用铁皮制作的,则制作这个长方体容器需要多少平方分米铁皮?(不计损耗)
21.学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:
(1)当桌子上放有x(个)碟子时,请写出此时碟子的高度(用含x的式子表示);
(2)桌面上整齐地摆放几摞碟子,分别从三个方向上看,其三种形状图如下图所示,厨房师傅想把它们整齐叠成一摞,求叠成一摞后的高度.
碟子的个数
碟子的高度(单位:
cm)
1
2
2
2+1.5
3
2+3
4
2+4.5
…
…
22.将立方体纸盒沿某些棱剪开,且使六个面连在一起,然后铺平,可以得到其表面展开图的平面图形.
(1)以下两个方格图中的阴影部分能表示立方体表面展开图的是
(填A或B).
(2)在以下方格图中,画一个与(1)中呈现的阴影部分不相似(包括不全等)的立方体表面展开图.(用阴影表示)
(3)如图中的实线是立方体纸盒的剪裁线,请将其表面展开图画在右图的方格图中.(用阴影表示)
23.把棱长为1cm的若干个小正方体摆放成如图所示的几何体,然后在露出的表面上涂上颜色(不含底面)
(1)该几何体中有
小正方体?
(2)其中两面被涂到的有
个小正方体;没被涂到的有
个小正方体;
(3)求出涂上颜色部分的总面积.
24.如图是一张长方形纸片,长为,长为.
(1)若将此长方形纸片绕它的一边所在直线旋转一周,则形成的几何体是______;
(2)若将这个长方形纸片绕边所在直线旋转一周,则形成的几何体的体积是____(结果保留);
(3)若将这个长方形纸片绕它的一边所在直线旋转一周,求形成的几何体的表面积(结果保留).
25.十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在一个有趣的关系式,这个关系式被称为欧拉公式.请你观察下列几种简单的多面体模型,解答下列问题:
(1)完成表格:
多面体
顶点数(V)
面数(F)
棱数(E)
四面体
4
4
6
长方体
8
6
12
八面体
6
8
12
某多面体
20
30
你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是
F=
;(用
含
V、E
的式子表示)
(2)如果一个多面体每个顶点处都有a条棱,那么这个多面体的棱数(E)与顶点数(V)之间的关系式为
E=
a×V
.现有一个二十面体,有12个顶点,每个顶点处有
5
条棱,那么该二十面体有多少条棱?
(3)某个玻璃饰品的外形是简单多面体,它的外表面是由三角形和六边形两种多边形用含
n
的代数式表示)拼接而成,且有
18个顶点,每个顶点处都有4
条棱,设该多面体表面三角形的个数为
m,六边形的个数为
n,求m+n
的值.
26.如图所示,在一张正方形纸片的四个角上各剪去一个同样大小的正方形,然后把剩下的部分折成一个无盖的长方体盒子.请回答下列问题:
(1)剪去的小正方形的边长与折成的无盖长方体盒子的高之间的大小关系为
;
(2)如果设原来这张正方形纸片的边长为,所折成的无盖长方体盒子的高为,那么,这个无盖长方体盒子的容积可以表示为
;
(3)如果原正方形纸片的边长为,剪去的小正方形的边长按整数值依次变化,即分别取
时,计算折成
的无盖长方体盒子的容积得到下表,由此可以判断,当剪去的小正方形边长为
时,折成的无盖长方体盒子的容积最大
剪去的小正方
形的边长
1
2
3
4
5
6
7
8
9
10
折成的无盖长方体的容积
324
576
500
384
252
128
36
0
答案
一、选择题
1.C
2.B.
3.C
4.B.
5.A.
6.D
7.B
8.B.
9.D.
10.C
11.A.
12.D.
13.C
14.D.
二、填空题
15.21
16.③
②
①
17.4
18.17
三、解答题
19.观察图形可知,张度搭成的图形从正面看到的图形是,符合题意;
从上面看到的图形是,符合题意,
∴张度搭成的立体图形是正确的;
李磊搭成的图形从正面看到的图形是,符合题意;
从上面看到的图形是,不符合题意,
∴李磊搭成的立体图形是错误的.
20.解:(1)设
AB=BC,BB’=3AB,
由这个容器的容积为192立方分米,
(分米).
(2)
长方体的表面积为:
(平方分米),
制作这个长方体容器需要平方分米的铁皮.
21.(1)由图可知,每增加一个碟子高度增加1.5cm,桌子上放有x个碟子时,高度为2+1.5(x?1)=1.5x+0.5;
(2)由图可知,共有3摞,左前一摞有5个,左后一摞有4个,右边前面一摞有3个,
共有:3+4+5=12个,叠成一摞后的高度=1.5×12+0.5=18.5cm.
答:叠成一摞后的高度为18.5
cm.
22.解:(1)两个方格图中的阴影部分能表示立方体表面展开图的是A,
故答案为:A.
(2)立方体表面展开图如图所示:
(3)将其表面展开图画在方格图中如图所示:
23.(1)该几何体中正方体的个数为9+4+1=14个;
(2)根据图中小正方体的位置可知:最底层外边中间的小正方体被涂到2个面,共4个,只有最底层正中间的小正方体没被涂到,
故答案为4;1;
(3)先算侧面--底层12个小面;
中层8个小面;
上层4个小面;
再算上面--上层1个
中层3个(正方体是可以移动的,不管放在哪里,它压住的面积总是它的底面积,也就是一个,所以中层是4减1个)底层(9-4)=5个,
∴总共12+8+4+1+3+5=33个小面.
∴涂上颜色部分的总面积=1133=33cm2.
24.(1)圆柱;
(2)
绕AB旋转得到的圆柱的底面半径为,高为,体积;
(3)绕边所在直线旋转得到的圆柱的底面半径为,高为,
表面积是:;
绕边所在直线旋转得到的圆柱的底面半径为,高为,
表面积是:.
答:形成的几何体的表面积是或.
25.解:(1)
多面体
顶点数()
面数()
棱数()
四面体
4
4
6
长方体
8
6
12
正八面体
6
8
12
正十二面体
20
12
30
(2)∵(条)
∴该二十面体共有30条棱.
(3))∵有18个顶点,每个顶点处都有4条棱,两点确定一条直线;
∴共有18×4÷2=36(条棱),
∵F=E?V+2
∴18+F-36=2,
解得:F=20,
∴m+n=20;
26.解:(1)由折叠可知,
剪去的小正方形的边长与折成的无盖长方体盒子的高之间的大小关系为相等,
故答案为:相等;
(2)这个无盖长方体盒子的容积=h(a-2h)(a-2h)=h(a-2h)2(cm3);
故答案为:h(a-2h)2;
(3)当剪去的小正方形的边长取2时,m=2×(20-2×2)2=512,
当剪去的小正方形的边长取3时,n=3×(20-2×3)2=588,
当剪去的小正方形的边长的值逐渐增大时,所得到的无盖长方体纸盒的容积的值先增大后减小,
当剪去的小正方形的边长为3cm时,所得到的无盖长方体纸盒的容积最大.
