人教版七年级数学上册试题 一课一练 4.1 《 几何图形》习题2(word版含答案)
文档属性
| 名称 | 人教版七年级数学上册试题 一课一练 4.1 《 几何图形》习题2(word版含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 311.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-29 00:00:00 | ||
图片预览



文档简介
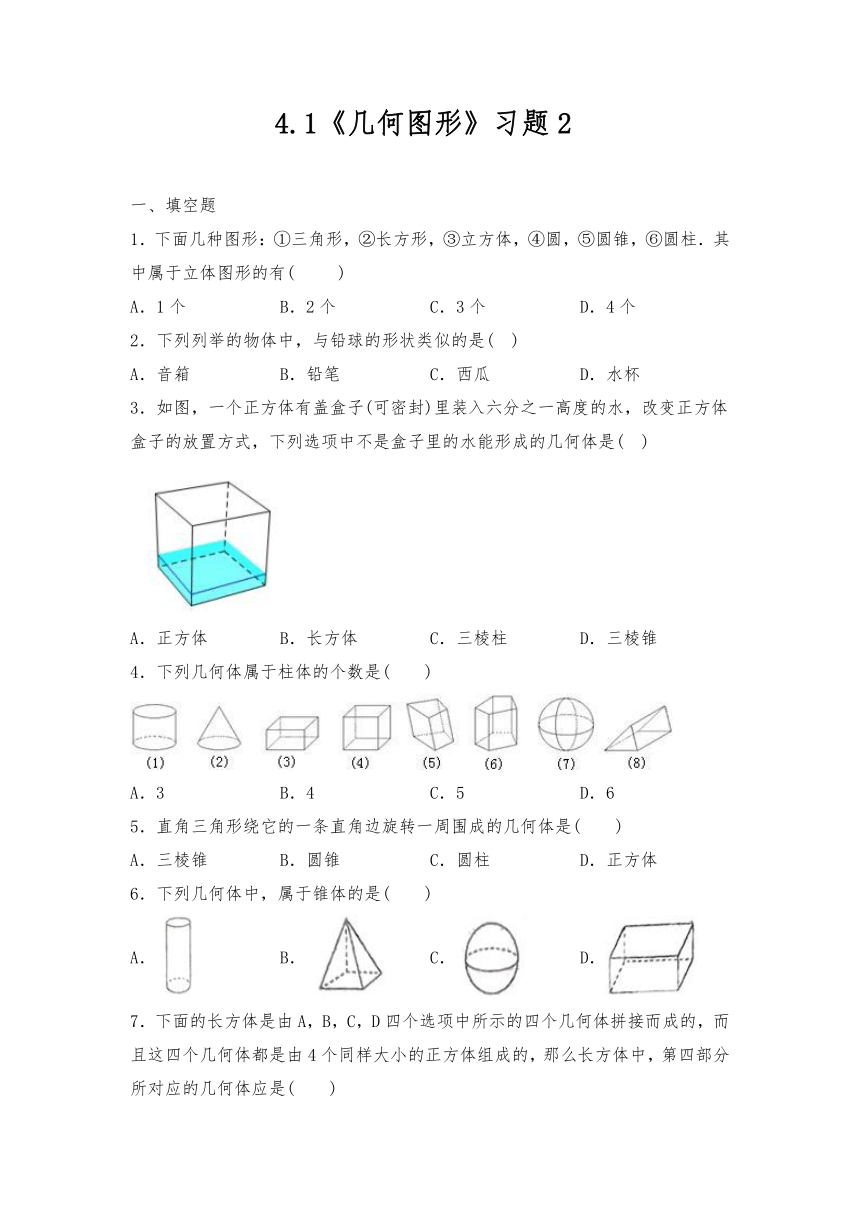
4.1《几何图形》习题2
一、填空题
1.下面几种图形:①三角形,②长方形,③立方体,④圆,⑤圆锥,⑥圆柱.其中属于立体图形的有(
)
A.1个
B.2个
C.3个
D.4个
2.下列列举的物体中,与铅球的形状类似的是(
)
A.音箱
B.铅笔
C.西瓜
D.水杯
3.如图,一个正方体有盖盒子(可密封)里装入六分之一高度的水,改变正方体盒子的放置方式,下列选项中不是盒子里的水能形成的几何体是(
)
A.正方体
B.长方体
C.三棱柱
D.三棱锥
4.下列几何体属于柱体的个数是(
)
A.3
B.4
C.5
D.6
5.直角三角形绕它的一条直角边旋转一周围成的几何体是( )
A.三棱锥
B.圆锥
C.圆柱
D.正方体
6.下列几何体中,属于锥体的是(
)
A.
B.
C.
D.
7.下面的长方体是由A,B,C,D四个选项中所示的四个几何体拼接而成的,而且这四个几何体都是由4个同样大小的正方体组成的,那么长方体中,第四部分所对应的几何体应是( )
A.
B.
C.
D.
8.如图,含有曲面的几何体编号是(
)
A.①②
B.①③
C.②③
D.②④
9.围成下列这些立体图形的各个面中,都是平的面为(
)
A.
B.
C.
D.
10.下图几何体面的个数为(
)
A.
B.
C.
D.
11.不透明袋子中装有一个几何体模型,两位同学摸该模型并描述它的特征.甲同学:它有4个面是三角形;乙同学:它有8条棱.该模型的形状对应的立体图形可能是( )
A.三棱柱
B.四棱柱
C.三棱锥
D.四棱锥
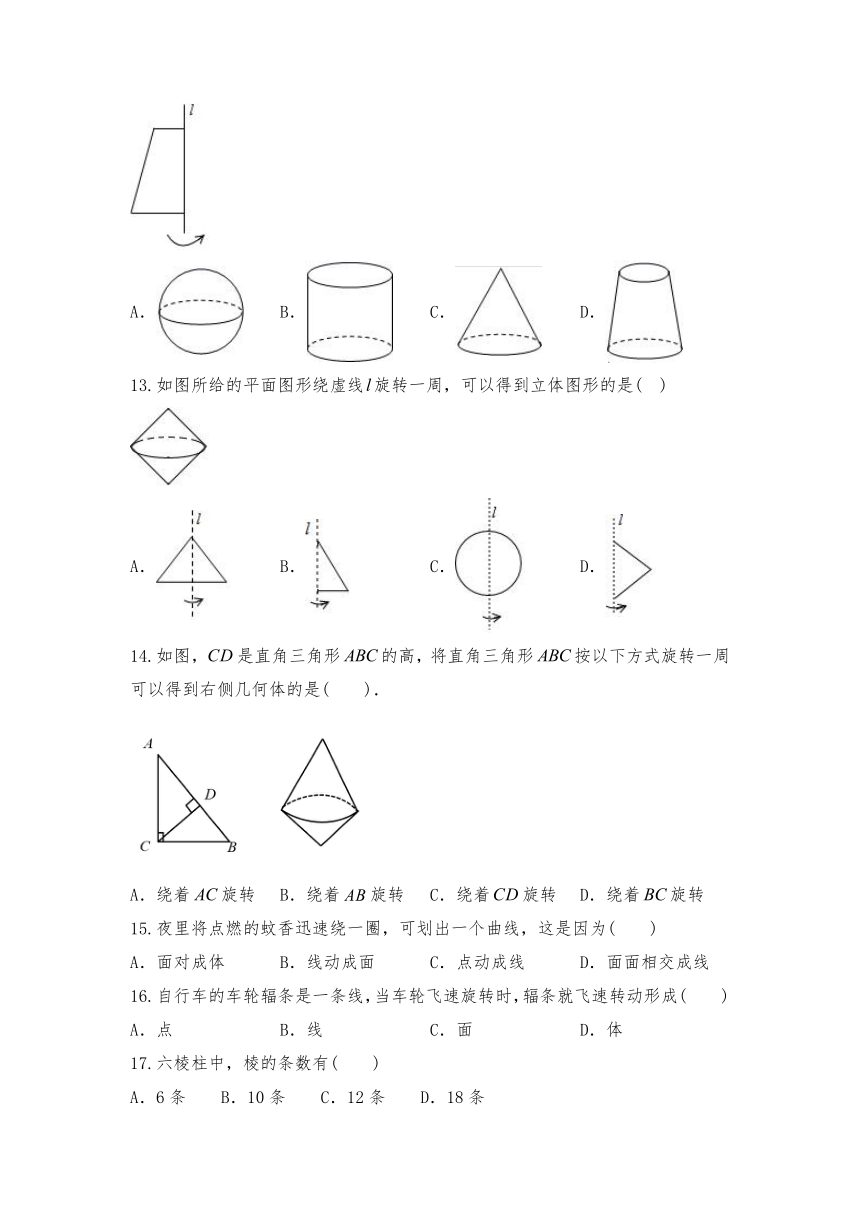
12.将下列如图的平面图形绕轴l旋转一周,可以得到的立体图形是( )
A.
B.
C.
D.
13.如图所给的平面图形绕虚线旋转一周,可以得到立体图形的是(
)
A.
B.
C.
D.
14.如图,是直角三角形的高,将直角三角形按以下方式旋转一周可以得到右侧几何体的是(
).
A.绕着旋转
B.绕着旋转
C.绕着旋转
D.绕着旋转
15.夜里将点燃的蚊香迅速绕一圈,可划出一个曲线,这是因为(
)
A.面对成体
B.线动成面
C.点动成线
D.面面相交成线
16.自行车的车轮辐条是一条线,当车轮飞速旋转时,辐条就飞速转动形成( )
A.点
B.线
C.面
D.体
17.六棱柱中,棱的条数有( )
A.6条
B.10条
C.12条
D.18条
18.观察下图,把左边的图形绕着给定的直线旋转一周后,可能形成的立体图形是(?
?)
A.
B.
C.
D.
19.下列四个图形中,不能作为正方体的展开图的是( )
A.
B.
C.
D.
20.下列各图中,可以是一个正方体的平面展开图的是(
)
A.
B.
C.
D.
21.下列图形中,是正方体表面展开图的是(
)
A.
B.
C.
D.
22.如图,将甲、乙、丙、丁四个小正方形中的一个剪掉,使余下的部分不能围成一个正方体,剪掉的这个小正方形是
A.甲
B.乙
C.丙
D.丁
23.图1和图2中所有的正方形都全等,将图1的正方形放在图2中的①②③④某一位置,所组成的图形不能围成正方体的位置是( )
A.①
B.②
C.③
D.④
24.下列四个图形中,不是正方体展开图的( )
A.
B.
C.
D.
25.下列图形中,经过折叠不能围成正方体的是( )
A.
B.
C.
D.
二、填空题
1.一个棱柱有12个面,它有__________个顶点,___________条棱.
2.这是一个_______体,它的长是_______
cm,宽是_______
cm,高是_______
cm.棱长总和是_______cm.
3.正方体有个6面,每个面都是_______形,面积都_______.
4.如图所示的几何体的名称是____,它由____个面组成,它有____个顶点,经过每个顶点有____条边.
5.一个圆柱和一个圆锥的底面圆的半径与高都分别相等,它们的体积差是24立方厘米,圆柱的体积是______立方厘米.
6.已知长方形的长为10cm,宽为4cm,将长方形绕边所在直线旋转后形成的立体图形的体积为______.
7.已知长方形长为5,宽为2,将其绕它的一条边所在的直线旋转一周,得到一个几何体,该几何体的体积为__________.(结果保留)
8.长为4,宽为2的矩形绕其一边旋转构成一个圆柱的最大体积为___
(结果保留π).
9.笔尖在纸上快速滑动写出英文字母C,这说明了_____.
三、解答题
1.我们曾学过圆柱的体积计算公式:(R是圆柱底面半径,h为圆柱的高),现有一个长方形,长为2cm,宽为1cm,以它的一边所在的直线为轴旋转一周,得到的几何体的体积是多少?
2.一个正方体的棱长是12厘米,这个正方体的体积是多少?
3.小名准备制作一个封闭的正方体盒子,他先用5个大小一样的正方形制成如图所示的拼接图形(实线部分),经折叠后发现还少一个面,你能在图中的拼接图形上再接一个正方形画出阴影,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子吗?请在下面的图①和图②中画出两种不同的补充方法.
4.如图是一个正方体的平面展开图,标注了A字母的是正方体的正面,如果正方体的左面与右面标注的式子相等.
(1)求x的值.
(2)求正方体的上面和底面的数字和.
答案
一、选择题
1.C.2.C.3.A.4.D.5.B.6.B.7.A.8.C.9.B.10.A.
11.D12.D.13.D.14.B15.C.16.C.17.D.18.C19.D20.C.
21.C.22.D23.A.24.D25.A.
二、填空题
1.20
30
2.长方;25;12;18
;220.
3.正方;相等.
4.五棱柱、7、10、3.
5.36
6.400πcm3或160πcm3
7.或
8.32π
9.点动成线
三、解答题
1.分两种情况:①绕长所在的直线为轴旋转一周,体积为;
②绕宽所在的直线为轴旋转一周,体积为;
故体积为或.
2.V=12?
=1728(cm?)
答:这个正方体的体积是1728cm?.
3.解:如图所示:
新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.
4.解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“A”与“-2”是相对面,
“3”与“1”是相对面,
“x”与“3x-2”是相对面,
(1)∵正方体的左面与右面标注的式子相等,
∴x=3x-2,
解得x=1;
(2)∵标注了A字母的是正方体的正面,左面与右面标注的式子相等,
∴上面和底面上的两个数字3和1,
∴3+1=4.
一、填空题
1.下面几种图形:①三角形,②长方形,③立方体,④圆,⑤圆锥,⑥圆柱.其中属于立体图形的有(
)
A.1个
B.2个
C.3个
D.4个
2.下列列举的物体中,与铅球的形状类似的是(
)
A.音箱
B.铅笔
C.西瓜
D.水杯
3.如图,一个正方体有盖盒子(可密封)里装入六分之一高度的水,改变正方体盒子的放置方式,下列选项中不是盒子里的水能形成的几何体是(
)
A.正方体
B.长方体
C.三棱柱
D.三棱锥
4.下列几何体属于柱体的个数是(
)
A.3
B.4
C.5
D.6
5.直角三角形绕它的一条直角边旋转一周围成的几何体是( )
A.三棱锥
B.圆锥
C.圆柱
D.正方体
6.下列几何体中,属于锥体的是(
)
A.
B.
C.
D.
7.下面的长方体是由A,B,C,D四个选项中所示的四个几何体拼接而成的,而且这四个几何体都是由4个同样大小的正方体组成的,那么长方体中,第四部分所对应的几何体应是( )
A.
B.
C.
D.
8.如图,含有曲面的几何体编号是(
)
A.①②
B.①③
C.②③
D.②④
9.围成下列这些立体图形的各个面中,都是平的面为(
)
A.
B.
C.
D.
10.下图几何体面的个数为(
)
A.
B.
C.
D.
11.不透明袋子中装有一个几何体模型,两位同学摸该模型并描述它的特征.甲同学:它有4个面是三角形;乙同学:它有8条棱.该模型的形状对应的立体图形可能是( )
A.三棱柱
B.四棱柱
C.三棱锥
D.四棱锥
12.将下列如图的平面图形绕轴l旋转一周,可以得到的立体图形是( )
A.
B.
C.
D.
13.如图所给的平面图形绕虚线旋转一周,可以得到立体图形的是(
)
A.
B.
C.
D.
14.如图,是直角三角形的高,将直角三角形按以下方式旋转一周可以得到右侧几何体的是(
).
A.绕着旋转
B.绕着旋转
C.绕着旋转
D.绕着旋转
15.夜里将点燃的蚊香迅速绕一圈,可划出一个曲线,这是因为(
)
A.面对成体
B.线动成面
C.点动成线
D.面面相交成线
16.自行车的车轮辐条是一条线,当车轮飞速旋转时,辐条就飞速转动形成( )
A.点
B.线
C.面
D.体
17.六棱柱中,棱的条数有( )
A.6条
B.10条
C.12条
D.18条
18.观察下图,把左边的图形绕着给定的直线旋转一周后,可能形成的立体图形是(?
?)
A.
B.
C.
D.
19.下列四个图形中,不能作为正方体的展开图的是( )
A.
B.
C.
D.
20.下列各图中,可以是一个正方体的平面展开图的是(
)
A.
B.
C.
D.
21.下列图形中,是正方体表面展开图的是(
)
A.
B.
C.
D.
22.如图,将甲、乙、丙、丁四个小正方形中的一个剪掉,使余下的部分不能围成一个正方体,剪掉的这个小正方形是
A.甲
B.乙
C.丙
D.丁
23.图1和图2中所有的正方形都全等,将图1的正方形放在图2中的①②③④某一位置,所组成的图形不能围成正方体的位置是( )
A.①
B.②
C.③
D.④
24.下列四个图形中,不是正方体展开图的( )
A.
B.
C.
D.
25.下列图形中,经过折叠不能围成正方体的是( )
A.
B.
C.
D.
二、填空题
1.一个棱柱有12个面,它有__________个顶点,___________条棱.
2.这是一个_______体,它的长是_______
cm,宽是_______
cm,高是_______
cm.棱长总和是_______cm.
3.正方体有个6面,每个面都是_______形,面积都_______.
4.如图所示的几何体的名称是____,它由____个面组成,它有____个顶点,经过每个顶点有____条边.
5.一个圆柱和一个圆锥的底面圆的半径与高都分别相等,它们的体积差是24立方厘米,圆柱的体积是______立方厘米.
6.已知长方形的长为10cm,宽为4cm,将长方形绕边所在直线旋转后形成的立体图形的体积为______.
7.已知长方形长为5,宽为2,将其绕它的一条边所在的直线旋转一周,得到一个几何体,该几何体的体积为__________.(结果保留)
8.长为4,宽为2的矩形绕其一边旋转构成一个圆柱的最大体积为___
(结果保留π).
9.笔尖在纸上快速滑动写出英文字母C,这说明了_____.
三、解答题
1.我们曾学过圆柱的体积计算公式:(R是圆柱底面半径,h为圆柱的高),现有一个长方形,长为2cm,宽为1cm,以它的一边所在的直线为轴旋转一周,得到的几何体的体积是多少?
2.一个正方体的棱长是12厘米,这个正方体的体积是多少?
3.小名准备制作一个封闭的正方体盒子,他先用5个大小一样的正方形制成如图所示的拼接图形(实线部分),经折叠后发现还少一个面,你能在图中的拼接图形上再接一个正方形画出阴影,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子吗?请在下面的图①和图②中画出两种不同的补充方法.
4.如图是一个正方体的平面展开图,标注了A字母的是正方体的正面,如果正方体的左面与右面标注的式子相等.
(1)求x的值.
(2)求正方体的上面和底面的数字和.
答案
一、选择题
1.C.2.C.3.A.4.D.5.B.6.B.7.A.8.C.9.B.10.A.
11.D12.D.13.D.14.B15.C.16.C.17.D.18.C19.D20.C.
21.C.22.D23.A.24.D25.A.
二、填空题
1.20
30
2.长方;25;12;18
;220.
3.正方;相等.
4.五棱柱、7、10、3.
5.36
6.400πcm3或160πcm3
7.或
8.32π
9.点动成线
三、解答题
1.分两种情况:①绕长所在的直线为轴旋转一周,体积为;
②绕宽所在的直线为轴旋转一周,体积为;
故体积为或.
2.V=12?
=1728(cm?)
答:这个正方体的体积是1728cm?.
3.解:如图所示:
新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.
4.解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“A”与“-2”是相对面,
“3”与“1”是相对面,
“x”与“3x-2”是相对面,
(1)∵正方体的左面与右面标注的式子相等,
∴x=3x-2,
解得x=1;
(2)∵标注了A字母的是正方体的正面,左面与右面标注的式子相等,
∴上面和底面上的两个数字3和1,
∴3+1=4.
