8.5.1直线与直线平行-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册练习(Word含答案解析)
文档属性
| 名称 | 8.5.1直线与直线平行-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册练习(Word含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 345.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-29 12:41:34 | ||
图片预览




文档简介
直线与直线平行练习
一、单选题
若OA//O'A',OB//O'B',且∠AOB=130?,则∠A'O'B'等于(????)
A. 130? B. 50? C. 130?或50? D. 不能确定
在三棱锥P?ABC中,PB⊥BC,E,D,F分别是AB,PA,AC的中点,则∠DEF=?(????)
A. 30° B. 45° C. 60° D. 90°
直线a与直线b相交,直线c也与直线b相交,则直线a与直线c的位置关系是(????)
A. 相交 B. 平行 C. 异面 D. 以上都有可能
已知AB//PQ,BC//QR,∠ABC=30°,则∠PQR=(????)
A. 30° B. 30°或150° C. 150° D. 30°或120°
在三棱台A1B1C1?ABC中,G,H分别是AB,AC的中点,则GH与B1C1? (??? )
A. 相交 B. 异面 C. 平行 D. 垂直
已知a,b,c为三条不重合的直线,α,β是两个不重合的平面,给出下列四个说法:①a?//b,b?//c?a?//c;②a?//α,b?//α?a?//b;③a?//α,β?//α?a?//β;④a?α,b?α,a?//b?a?//α.其中说法正确的是(????)
A. ①④ B. ①② C. ②③ D. ③④
在底面为正方形的四棱锥P??ABCD中,PA⊥底面ABCD,∠PDA=45°,则异面直线PB与AC所成的角为(? )
A. 90° B. 60° C. 45° D. 30°
如图,OA,OB,OC为不共面的三条线段,点A1,B1,C1分别是OA,OB,OC上的点(不含端点),且OA1OA=OB1OB=OC1OC,则△A1B1C1与△ABC? (??? )
A. 相似
B. 全等
C. 不相似
D. 仅有一角相等
如图所示,在正方体ABCD—A1B1C1D1中,E,F分别是AB1,BC1的中点,则异面直线EF与C1D所成的角为(? ?)
A. 30° B. 45° C. 60° D. 90°
已知正方体ABCD?A1B1C1D1的棱长为2,点P在棱AD上,过点P作该正方体的截面,当截面平行于平面B1D1C且面积为3时,线段AP的长为(??? )
A. 2 B. 1 C. 3 D. 32
已知直三棱柱ABC?A1B1C1的侧棱长为2,AB⊥BC,AB=BC=2.过AB,BB1的中点E,F作平面α与平面AA1C1C垂直,则所得截面周长为(????)
A. 22+6 B. 2+26 C. 32+6 D. 32+26
已知直三棱柱ABC?A1B1C1的侧棱长为2,AB⊥BC,AB=BC=2.过AB,BB1的中点E,F作平面α与平面AA1C1C垂直,则所得截面周长为
A. 22+6 B. 2+26 C. 32+6 D. 32+26
二、单空题
空间两个角α,β的两边分别对应平行,且α=60?,则β=??????????.
在四棱锥P?ABCD中,E,F,G,H分别是PA,PC,AB,BC的中点,若EF=2,则GH=________.
在空间四边形ABCD中,如图所示,AEAB=AHAD=12,CFCB=CGCD=23,则EH与FG的位置关系是________.
如图所示,在空间四边形ABCD中,E,H分别是AB,AD的中点,F,G分别是CB,CD上的点,且CFCB=CGCD=23,若BD?=6,四边形EFGH的面积为28,则直线EH,FG之间的距离为??????????.
三、解答题
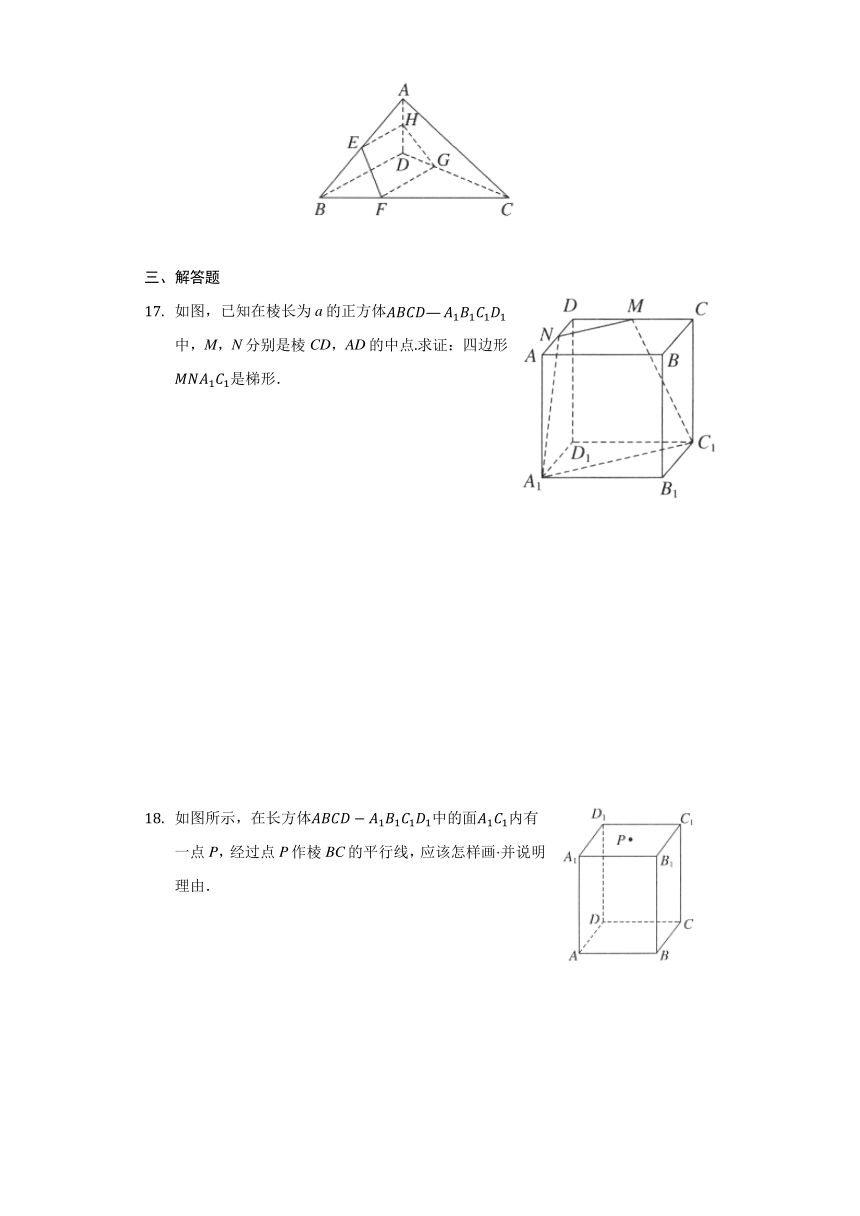
如图,已知在棱长为a的正方体ABCD—A1B1C1D1中,M,N分别是棱CD,AD的中点.求证:四边形MNA1C1是梯形.
如图所示,在长方体ABCD?A1B1C1D1中的面A1C1内有一点P,经过点P作棱BC的平行线,应该怎样画?并说明理由.
如图所示,在正方体AB?CD?A1B1C1D1中,E,E1分别是棱AD,A1D1的中点.求证:∠BEC=∠B1E1C1.
如图所示,四边形ABEF和ABCD都是直角梯形,∠BAD=∠FAB=90?,BC//AD,BC=12AD,BE//FA,BE=12FA,G,H分别为FA,FD的中点.
(1)证明:四边形BCHG是平行四边形;
(2)C,D,F,E四点是否共面?为什么?
答案和解析
1.【答案】C
【解答】
解:若∠AOB和∠A'O'B'的在同一平面内,
则根据两直线平行,内错角相等,
可得:∠AOB=∠A'MB=∠A'O'B',
∠COB=∠O'MB
,
则∠A'MB+∠O'MB=180°,
既有:∠COB+∠A'O'B'=180°,
即∠AOB和∠A'O'B'的关系为相等或互补.
所以∠A'O'B'等于130?或50?
若∠AOB和∠A'O'B'的不在同一平面内,
则根据平行直线的性质可知,结论同样成立.
2.【答案】D
【解析】
解:如图,
∵D,E分别为线段PA,AB的中点,
∴DE//PB,(中位线定理)
∠DEF即PB与异面直线EF的夹角,
∵F为线段AC的中点,
EF//BC,(中位线定理)
∠DEF即PB与BC的夹角,
∴∠DEF=∠PBC,
∵PB⊥BC,即∠PBC=90°,
∴∠DEF=90°.
故选:D.
3.【答案】D
【解答】
解:如图所示,在长方体ABCD?A1B1C1D1中,
AB与AA1相交,A1B1与AA1相交,
所以由图知AB//A1B1;
又AD与AA1相交,AB与AA1相交
所以由图知AB与AD相交;
又A1D1与AA1相交,AB与AA1相交,
所以由图知AB与A1D1异面.
4.【答案】B
【解析】【试题解析】
解:由题意知AB//PQ,BC//QR,∠ABC=30°,
根据空间平行公理知,一个角的两边分别平行于另一个角的两边,则这两个角相等或互补
所以∠PQR等于30°或150°
5.【答案】C
【解析】
解:因为G,H分别是AB,AC的中点,所以GH?//?BC,
又由三棱台的性质得BC?//?B1C1,
由平行公理推论,所以GH?//?B1C1.
故选C.
6.【答案】A
【解析】
【解答】
解:①由a//b,b//c,根据平行公理,可得a//c,故①正确;
②由a//α,b//α不一定有a//b,还可以是相交,故②错误;
③由a//α,β//α,可得a//β或a?β,故③错误;
④直接根据线面平行平行的判定定理可知④正确;
故选A.
7.【答案】B
【解答】
解:由题意底面ABCD为正方形,PA⊥平面ABCD,?
分别过P,D点作AD,AP的平行线交于M,连接CM,AM,
则PM//AD,PM=AD,
由底面ABCD为正方形,可得AD//BC,AD=BC,
所以PM//BC,PM=BC,所以四边形PBCM是平行四边形,
所以PB//CM.
故∠ACM或其补角就是异面直线PB与AC所成的角.
因为PA⊥平面ABCD,且AD?平面ABCD,所以PA⊥AD,
又因为∠PDA=45°,所以PA=AD.
设PA=AD=a,则ΔACM中,AM=2a,AC=2a,CM=2a,
所以ΔACM是等边三角形,即∠ACM=60°,
即异面直线PB与AC所成的角为60°.?
故选B.
8.【答案】A
【解答】
解:在△OAB中,因为OA1OA=OB1OB,所以A1B1?//?AB.
同理可得A1C1?//?AC,B1C1?//?BC,
所以∠C1A1B1=∠CAB,∠A1B1C1=∠ABC,
所以△A1B1C1∽△ABC,
9.【答案】C
【解答】
解:如下图:
连接A1C1,A1D.
取A1B1、B1C1的中点分别为G、H,
连接EG、GH、HF,则GH//A1C1.
因为E,F分别是AB1,BC1的中点,所以GE=?//12A1A,HF=?//12B1B,
而ABCD?A1B1C1D1是正方体,因此GE=?//HF,
即四边形GEFH是平行四边形,所以EF//GH,
因此EF//A1C1,
所以异面直线EF与C1D所成的角就是直线A1C1与C1D所成的角(或补角),即∠A1C1D.
又因为ABCD?A1B1C1D1是正方体,所以ΔA1C1D是正三角形,
因此∠A1C1D=60°,即异面直线EF与C1D所成的角为60°.
10.【答案】A
【解答】
解:如图,三角形B1D1C是边长为B1D1的正三角形,B1D1=22,
故SΔB1D1C=34×222=23,
由正方体的几何特征可知,B1C//A1D,B1C//平面A1D,B1C?平面B1D1C,
平面A1D与平面B1D1C有公共点D1,必存在过D1点的交线l,
故交线l//B1C//A1D,
过点P作该正方体的截面,当截面平行于平面B1D1C时,两个平行平面与平面A1D的交线平行,
如图,过点P作该正方体的截面与平面A1D的交线PH,PH//A1D,交A1A于H点,
同理过点P作该正方体的截面与平面BD的交线PE,PE//BD,交AB于E点,
同理过点P作该正方体的截面与平面A1B的交线HE,HE//A1B,
即PH//B1C,PE//B1D1,HE//D1C,
由等角定理知△PEH与B1D1C是相似三角形,且均为正三角形,
相似比为1:2,故△PEH的边长为2,
故三棱锥A?PEH为正三棱锥A?PEH,且三条侧棱两两垂直,
故PA=22×PH=22×2=2,
故选A.
11.【答案】C
【解答】
解:如图:
因为ABC?A1B1C1是直三棱柱,AB⊥BC,AB=BC=2,
所以取AC的中点G,连接BG,取AG的中点H,连接EH,而E是AB的中点,
则BG⊥平面AA1C1C,EH⊥平面AA1C1C,
且AH=EH=12BG=22,EH//BG.
连接AC1、CA1交于O,连接GO,延长交A1C1于G1,则G1是A1C1的中点.
因为ABC?A1B1C1是直三棱柱,所以BGG1B1是矩形且O是GG1的中点,
因此连接FO,由F是BB1的中点知:FO⊥平面AA1C1C.
因为EH⊥平面AA1C1C,FO⊥平面AA1C1C,所以EH//FO,
因此EH与FO确定一个平面EFOH,而FO?平面EFOH,
所以平面EFOH是与平面AA1C1C垂直的平面α.
延长HO,交A1C1于H1,则HH1是平面α与三棱柱ABC?A1B1C1侧面AA1C1C的交线.
在矩形AA1C1C中,因为O是AC1的中点,所以C1H1=AH=22.
又因为在矩形AA1C1C中,AA1=2,AC=22,所以HH1=6.
又因为ABC?A1B1C1是直三棱柱,所以平面ABC//平面A1B1C1,
而平面α与平面A1B1C1有一个交点H1,
因此平面α与平面A1B1C1必相交于过H1的一条直线l,
不妨设直线l与直线B1C1交于K,则EH//KH1.
又因为EH//BG,BGG1B1是矩形,所以KH1//B1G1.
又因为C1H1=22=12C1G1,所以K是B1C1的中点,因此KH1=22.
连接KF,因为四边形AA1B1B和BB1C1C都是边长为2的正方形,因此KF=FE=2.
又因为平面EHH1KF是平面α与直三棱柱ABC?A1B1C1的截面,
所以所得截面周长为:KF+FE+EH+HH1+H1K
=2+2+22+6+22=32+6.
故选C.
12.【答案】C
【解答】
解:如图:
因为ABC?A1B1C1是直三棱柱,AB⊥BC,AB=BC=2,
所以取AC的中点G,连接BG,取AG的中点H,连接EH,而E是AB的中点,
则BG⊥平面AA1C1C,EH⊥平面AA1C1C,
且AH=EH=12BG=22,EH//BG.
连接AC1、CA1交于O,连接GO,延长交A1C1于G1,则G1是A1C1的中点.
因为ABC?A1B1C1是直三棱柱,所以BGG1B1是矩形且O是GG1的中点,
因此连接FO,由F是BB1的中点知:FO⊥平面AA1C1C.
因为EH⊥平面AA1C1C,FO⊥平面AA1C1C,所以EH//FO,
因此EH与FO确定一个平面EFOH,而FO?平面EFOH,
所以平面EFOH是与平面AA1C1C垂直的平面α.
延长HO,交A1C1于H1,则HH1是平面α与三棱柱ABC?A1B1C1侧面AA1C1C的交线.
在矩形AA1C1C中,因为O是AC1的中点,所以C1H1=AH=22.
又因为在矩形AA1C1C中,AA1=2,AC=22,所以HH1=6.
又因为ABC?A1B1C1是直三棱柱,所以平面ABC//平面A1B1C1,
而平面α与平面A1B1C1有一个交点H1,
因此平面α与平面A1B1C1必相交于过H1的一条直线l,
不妨设直线l与直线B1C1交于K,则EH//KH1.
又因为EH//BG,BGG1B1是矩形,所以KH1//B1G1.
又因为C1H1=22=12C1G1,所以K是B1C1的中点,因此KH1=22.
连接KF,因为四边形AA1B1B和BB1C1C都是边长为2的正方形,因此KF=FE=2.
又因为平面EHH1KF是平面α与直三棱柱ABC?A1B1C1的截面,
所以所得截面周长为:KF+FE+EH+HH1+H1K
=2+2+22+6+22=32+6.
故选C.
13.【答案】600或1200
【解答】
解:根据等角定理定理如果两个角的两边分别对应平行,则这两个角相等或互补,
可知角β为60°或120°.
故答案为60°或120°.
14.【答案】2
【解析】
解:∵E,F分别是PA,PC的中点,
∴EF=?//12AC,
∵G,H分别是AB,BC的中点,
∴GH=?//12AC,
由平行线传递性,等量替换,
得EF=?//GH,
∵EF=2,∴GH=2.
15.【答案】平行
【解答】
解:连接BD,
如图示:在△ABD中∵AEAB=AHAD,
∴EH?//?BD.
在△CBD中同理可证FG?//?BD.
故EH?//?FG.
故答案为平行.
16.【答案】8
【解析】
【分析】
【解答】
解:因为E,H分别是AB,AD的中点,BD=6cm,所以EH//BD,且EH=12BD=3cm,
因为CFCB=CGCD=23,又∠GCF=∠DCB,所以△CGF∽△CDB,所以GF//BD,且GF=23BD=4cm,
所以EH//GF,于是四边形EHGF为梯形,
设平行线EH,FG间的距离为hcm,即梯形EHGF的高为hcm,其面积为12(EH+GF)?=28.
即12(3+4)?=28,解得?=8.
故平行线EH,FG间的距离为8cm.
17.【答案】证明:如图,连结AC,
在中,
∵M,N分别是CD,AD的中点,
∴MN是△ACD的中位线,
∴MN//AC,且|MN|=12|AC|,
由正方体的性质得AC//A1C1,且|AC|=|A1C1|,
∴MN//A1C1,且|MN|=12|A1C1|,
即|MN|≠|A1C1|,
∴四边形MNA1C1是梯形.
18.【答案】解:如图所示,在面A1C1内过点P作直线EF//B1C1,交A1B1于点E,交C1D1于点F,则直线EF即为所求.
理由:因为EF//B1C1,BC//B1C1,所以EF//BC.
19.【答案】证明:∵E,E1分别为正方体ABCD?A1B1C1D1的棱AD,A1D1的中点.
又CC1//DD1,EE1//DD1,
故CC?1//EE1,且CC1=EE1,
所以四边形CC1E1E为平行四边形,所以EC//E1C1?,
同理可证BE//B1E1,
∴∠BEC=∠B1E1C1.
20.【答案】解:(1)∵G,H分别为FA,FD的中点,
∴GH//AD,且GH=12AD,
又BC//AD,且BC=12AD,
∴GH//BC,且GH=BC,
∴四边形BCHG为平行四边形.
(2)∵BE//AF,且BE=12AF,G为FA的中点,
∴BE//FG,且BE=FG,
∴四边形BEFG为平行四边形,∴EF//BG.
由(1)知BG//CH,∴EF//CH,∴EF与CH共面.
又D∈FH,∴C,D,F,E四点共面.
一、单选题
若OA//O'A',OB//O'B',且∠AOB=130?,则∠A'O'B'等于(????)
A. 130? B. 50? C. 130?或50? D. 不能确定
在三棱锥P?ABC中,PB⊥BC,E,D,F分别是AB,PA,AC的中点,则∠DEF=?(????)
A. 30° B. 45° C. 60° D. 90°
直线a与直线b相交,直线c也与直线b相交,则直线a与直线c的位置关系是(????)
A. 相交 B. 平行 C. 异面 D. 以上都有可能
已知AB//PQ,BC//QR,∠ABC=30°,则∠PQR=(????)
A. 30° B. 30°或150° C. 150° D. 30°或120°
在三棱台A1B1C1?ABC中,G,H分别是AB,AC的中点,则GH与B1C1? (??? )
A. 相交 B. 异面 C. 平行 D. 垂直
已知a,b,c为三条不重合的直线,α,β是两个不重合的平面,给出下列四个说法:①a?//b,b?//c?a?//c;②a?//α,b?//α?a?//b;③a?//α,β?//α?a?//β;④a?α,b?α,a?//b?a?//α.其中说法正确的是(????)
A. ①④ B. ①② C. ②③ D. ③④
在底面为正方形的四棱锥P??ABCD中,PA⊥底面ABCD,∠PDA=45°,则异面直线PB与AC所成的角为(? )
A. 90° B. 60° C. 45° D. 30°
如图,OA,OB,OC为不共面的三条线段,点A1,B1,C1分别是OA,OB,OC上的点(不含端点),且OA1OA=OB1OB=OC1OC,则△A1B1C1与△ABC? (??? )
A. 相似
B. 全等
C. 不相似
D. 仅有一角相等
如图所示,在正方体ABCD—A1B1C1D1中,E,F分别是AB1,BC1的中点,则异面直线EF与C1D所成的角为(? ?)
A. 30° B. 45° C. 60° D. 90°
已知正方体ABCD?A1B1C1D1的棱长为2,点P在棱AD上,过点P作该正方体的截面,当截面平行于平面B1D1C且面积为3时,线段AP的长为(??? )
A. 2 B. 1 C. 3 D. 32
已知直三棱柱ABC?A1B1C1的侧棱长为2,AB⊥BC,AB=BC=2.过AB,BB1的中点E,F作平面α与平面AA1C1C垂直,则所得截面周长为(????)
A. 22+6 B. 2+26 C. 32+6 D. 32+26
已知直三棱柱ABC?A1B1C1的侧棱长为2,AB⊥BC,AB=BC=2.过AB,BB1的中点E,F作平面α与平面AA1C1C垂直,则所得截面周长为
A. 22+6 B. 2+26 C. 32+6 D. 32+26
二、单空题
空间两个角α,β的两边分别对应平行,且α=60?,则β=??????????.
在四棱锥P?ABCD中,E,F,G,H分别是PA,PC,AB,BC的中点,若EF=2,则GH=________.
在空间四边形ABCD中,如图所示,AEAB=AHAD=12,CFCB=CGCD=23,则EH与FG的位置关系是________.
如图所示,在空间四边形ABCD中,E,H分别是AB,AD的中点,F,G分别是CB,CD上的点,且CFCB=CGCD=23,若BD?=6,四边形EFGH的面积为28,则直线EH,FG之间的距离为??????????.
三、解答题
如图,已知在棱长为a的正方体ABCD—A1B1C1D1中,M,N分别是棱CD,AD的中点.求证:四边形MNA1C1是梯形.
如图所示,在长方体ABCD?A1B1C1D1中的面A1C1内有一点P,经过点P作棱BC的平行线,应该怎样画?并说明理由.
如图所示,在正方体AB?CD?A1B1C1D1中,E,E1分别是棱AD,A1D1的中点.求证:∠BEC=∠B1E1C1.
如图所示,四边形ABEF和ABCD都是直角梯形,∠BAD=∠FAB=90?,BC//AD,BC=12AD,BE//FA,BE=12FA,G,H分别为FA,FD的中点.
(1)证明:四边形BCHG是平行四边形;
(2)C,D,F,E四点是否共面?为什么?
答案和解析
1.【答案】C
【解答】
解:若∠AOB和∠A'O'B'的在同一平面内,
则根据两直线平行,内错角相等,
可得:∠AOB=∠A'MB=∠A'O'B',
∠COB=∠O'MB
,
则∠A'MB+∠O'MB=180°,
既有:∠COB+∠A'O'B'=180°,
即∠AOB和∠A'O'B'的关系为相等或互补.
所以∠A'O'B'等于130?或50?
若∠AOB和∠A'O'B'的不在同一平面内,
则根据平行直线的性质可知,结论同样成立.
2.【答案】D
【解析】
解:如图,
∵D,E分别为线段PA,AB的中点,
∴DE//PB,(中位线定理)
∠DEF即PB与异面直线EF的夹角,
∵F为线段AC的中点,
EF//BC,(中位线定理)
∠DEF即PB与BC的夹角,
∴∠DEF=∠PBC,
∵PB⊥BC,即∠PBC=90°,
∴∠DEF=90°.
故选:D.
3.【答案】D
【解答】
解:如图所示,在长方体ABCD?A1B1C1D1中,
AB与AA1相交,A1B1与AA1相交,
所以由图知AB//A1B1;
又AD与AA1相交,AB与AA1相交
所以由图知AB与AD相交;
又A1D1与AA1相交,AB与AA1相交,
所以由图知AB与A1D1异面.
4.【答案】B
【解析】【试题解析】
解:由题意知AB//PQ,BC//QR,∠ABC=30°,
根据空间平行公理知,一个角的两边分别平行于另一个角的两边,则这两个角相等或互补
所以∠PQR等于30°或150°
5.【答案】C
【解析】
解:因为G,H分别是AB,AC的中点,所以GH?//?BC,
又由三棱台的性质得BC?//?B1C1,
由平行公理推论,所以GH?//?B1C1.
故选C.
6.【答案】A
【解析】
【解答】
解:①由a//b,b//c,根据平行公理,可得a//c,故①正确;
②由a//α,b//α不一定有a//b,还可以是相交,故②错误;
③由a//α,β//α,可得a//β或a?β,故③错误;
④直接根据线面平行平行的判定定理可知④正确;
故选A.
7.【答案】B
【解答】
解:由题意底面ABCD为正方形,PA⊥平面ABCD,?
分别过P,D点作AD,AP的平行线交于M,连接CM,AM,
则PM//AD,PM=AD,
由底面ABCD为正方形,可得AD//BC,AD=BC,
所以PM//BC,PM=BC,所以四边形PBCM是平行四边形,
所以PB//CM.
故∠ACM或其补角就是异面直线PB与AC所成的角.
因为PA⊥平面ABCD,且AD?平面ABCD,所以PA⊥AD,
又因为∠PDA=45°,所以PA=AD.
设PA=AD=a,则ΔACM中,AM=2a,AC=2a,CM=2a,
所以ΔACM是等边三角形,即∠ACM=60°,
即异面直线PB与AC所成的角为60°.?
故选B.
8.【答案】A
【解答】
解:在△OAB中,因为OA1OA=OB1OB,所以A1B1?//?AB.
同理可得A1C1?//?AC,B1C1?//?BC,
所以∠C1A1B1=∠CAB,∠A1B1C1=∠ABC,
所以△A1B1C1∽△ABC,
9.【答案】C
【解答】
解:如下图:
连接A1C1,A1D.
取A1B1、B1C1的中点分别为G、H,
连接EG、GH、HF,则GH//A1C1.
因为E,F分别是AB1,BC1的中点,所以GE=?//12A1A,HF=?//12B1B,
而ABCD?A1B1C1D1是正方体,因此GE=?//HF,
即四边形GEFH是平行四边形,所以EF//GH,
因此EF//A1C1,
所以异面直线EF与C1D所成的角就是直线A1C1与C1D所成的角(或补角),即∠A1C1D.
又因为ABCD?A1B1C1D1是正方体,所以ΔA1C1D是正三角形,
因此∠A1C1D=60°,即异面直线EF与C1D所成的角为60°.
10.【答案】A
【解答】
解:如图,三角形B1D1C是边长为B1D1的正三角形,B1D1=22,
故SΔB1D1C=34×222=23,
由正方体的几何特征可知,B1C//A1D,B1C//平面A1D,B1C?平面B1D1C,
平面A1D与平面B1D1C有公共点D1,必存在过D1点的交线l,
故交线l//B1C//A1D,
过点P作该正方体的截面,当截面平行于平面B1D1C时,两个平行平面与平面A1D的交线平行,
如图,过点P作该正方体的截面与平面A1D的交线PH,PH//A1D,交A1A于H点,
同理过点P作该正方体的截面与平面BD的交线PE,PE//BD,交AB于E点,
同理过点P作该正方体的截面与平面A1B的交线HE,HE//A1B,
即PH//B1C,PE//B1D1,HE//D1C,
由等角定理知△PEH与B1D1C是相似三角形,且均为正三角形,
相似比为1:2,故△PEH的边长为2,
故三棱锥A?PEH为正三棱锥A?PEH,且三条侧棱两两垂直,
故PA=22×PH=22×2=2,
故选A.
11.【答案】C
【解答】
解:如图:
因为ABC?A1B1C1是直三棱柱,AB⊥BC,AB=BC=2,
所以取AC的中点G,连接BG,取AG的中点H,连接EH,而E是AB的中点,
则BG⊥平面AA1C1C,EH⊥平面AA1C1C,
且AH=EH=12BG=22,EH//BG.
连接AC1、CA1交于O,连接GO,延长交A1C1于G1,则G1是A1C1的中点.
因为ABC?A1B1C1是直三棱柱,所以BGG1B1是矩形且O是GG1的中点,
因此连接FO,由F是BB1的中点知:FO⊥平面AA1C1C.
因为EH⊥平面AA1C1C,FO⊥平面AA1C1C,所以EH//FO,
因此EH与FO确定一个平面EFOH,而FO?平面EFOH,
所以平面EFOH是与平面AA1C1C垂直的平面α.
延长HO,交A1C1于H1,则HH1是平面α与三棱柱ABC?A1B1C1侧面AA1C1C的交线.
在矩形AA1C1C中,因为O是AC1的中点,所以C1H1=AH=22.
又因为在矩形AA1C1C中,AA1=2,AC=22,所以HH1=6.
又因为ABC?A1B1C1是直三棱柱,所以平面ABC//平面A1B1C1,
而平面α与平面A1B1C1有一个交点H1,
因此平面α与平面A1B1C1必相交于过H1的一条直线l,
不妨设直线l与直线B1C1交于K,则EH//KH1.
又因为EH//BG,BGG1B1是矩形,所以KH1//B1G1.
又因为C1H1=22=12C1G1,所以K是B1C1的中点,因此KH1=22.
连接KF,因为四边形AA1B1B和BB1C1C都是边长为2的正方形,因此KF=FE=2.
又因为平面EHH1KF是平面α与直三棱柱ABC?A1B1C1的截面,
所以所得截面周长为:KF+FE+EH+HH1+H1K
=2+2+22+6+22=32+6.
故选C.
12.【答案】C
【解答】
解:如图:
因为ABC?A1B1C1是直三棱柱,AB⊥BC,AB=BC=2,
所以取AC的中点G,连接BG,取AG的中点H,连接EH,而E是AB的中点,
则BG⊥平面AA1C1C,EH⊥平面AA1C1C,
且AH=EH=12BG=22,EH//BG.
连接AC1、CA1交于O,连接GO,延长交A1C1于G1,则G1是A1C1的中点.
因为ABC?A1B1C1是直三棱柱,所以BGG1B1是矩形且O是GG1的中点,
因此连接FO,由F是BB1的中点知:FO⊥平面AA1C1C.
因为EH⊥平面AA1C1C,FO⊥平面AA1C1C,所以EH//FO,
因此EH与FO确定一个平面EFOH,而FO?平面EFOH,
所以平面EFOH是与平面AA1C1C垂直的平面α.
延长HO,交A1C1于H1,则HH1是平面α与三棱柱ABC?A1B1C1侧面AA1C1C的交线.
在矩形AA1C1C中,因为O是AC1的中点,所以C1H1=AH=22.
又因为在矩形AA1C1C中,AA1=2,AC=22,所以HH1=6.
又因为ABC?A1B1C1是直三棱柱,所以平面ABC//平面A1B1C1,
而平面α与平面A1B1C1有一个交点H1,
因此平面α与平面A1B1C1必相交于过H1的一条直线l,
不妨设直线l与直线B1C1交于K,则EH//KH1.
又因为EH//BG,BGG1B1是矩形,所以KH1//B1G1.
又因为C1H1=22=12C1G1,所以K是B1C1的中点,因此KH1=22.
连接KF,因为四边形AA1B1B和BB1C1C都是边长为2的正方形,因此KF=FE=2.
又因为平面EHH1KF是平面α与直三棱柱ABC?A1B1C1的截面,
所以所得截面周长为:KF+FE+EH+HH1+H1K
=2+2+22+6+22=32+6.
故选C.
13.【答案】600或1200
【解答】
解:根据等角定理定理如果两个角的两边分别对应平行,则这两个角相等或互补,
可知角β为60°或120°.
故答案为60°或120°.
14.【答案】2
【解析】
解:∵E,F分别是PA,PC的中点,
∴EF=?//12AC,
∵G,H分别是AB,BC的中点,
∴GH=?//12AC,
由平行线传递性,等量替换,
得EF=?//GH,
∵EF=2,∴GH=2.
15.【答案】平行
【解答】
解:连接BD,
如图示:在△ABD中∵AEAB=AHAD,
∴EH?//?BD.
在△CBD中同理可证FG?//?BD.
故EH?//?FG.
故答案为平行.
16.【答案】8
【解析】
【分析】
【解答】
解:因为E,H分别是AB,AD的中点,BD=6cm,所以EH//BD,且EH=12BD=3cm,
因为CFCB=CGCD=23,又∠GCF=∠DCB,所以△CGF∽△CDB,所以GF//BD,且GF=23BD=4cm,
所以EH//GF,于是四边形EHGF为梯形,
设平行线EH,FG间的距离为hcm,即梯形EHGF的高为hcm,其面积为12(EH+GF)?=28.
即12(3+4)?=28,解得?=8.
故平行线EH,FG间的距离为8cm.
17.【答案】证明:如图,连结AC,
在中,
∵M,N分别是CD,AD的中点,
∴MN是△ACD的中位线,
∴MN//AC,且|MN|=12|AC|,
由正方体的性质得AC//A1C1,且|AC|=|A1C1|,
∴MN//A1C1,且|MN|=12|A1C1|,
即|MN|≠|A1C1|,
∴四边形MNA1C1是梯形.
18.【答案】解:如图所示,在面A1C1内过点P作直线EF//B1C1,交A1B1于点E,交C1D1于点F,则直线EF即为所求.
理由:因为EF//B1C1,BC//B1C1,所以EF//BC.
19.【答案】证明:∵E,E1分别为正方体ABCD?A1B1C1D1的棱AD,A1D1的中点.
又CC1//DD1,EE1//DD1,
故CC?1//EE1,且CC1=EE1,
所以四边形CC1E1E为平行四边形,所以EC//E1C1?,
同理可证BE//B1E1,
∴∠BEC=∠B1E1C1.
20.【答案】解:(1)∵G,H分别为FA,FD的中点,
∴GH//AD,且GH=12AD,
又BC//AD,且BC=12AD,
∴GH//BC,且GH=BC,
∴四边形BCHG为平行四边形.
(2)∵BE//AF,且BE=12AF,G为FA的中点,
∴BE//FG,且BE=FG,
∴四边形BEFG为平行四边形,∴EF//BG.
由(1)知BG//CH,∴EF//CH,∴EF与CH共面.
又D∈FH,∴C,D,F,E四点共面.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
