9.2.3总体集中趋势的估计课件-2020-2021学年高一下学期数学人教A版(2019)必修第二册(共16张PPT)
文档属性
| 名称 | 9.2.3总体集中趋势的估计课件-2020-2021学年高一下学期数学人教A版(2019)必修第二册(共16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-29 13:29:24 | ||
图片预览





文档简介
(共16张PPT)
总体集中趋势的估计
安徽淮南第四中学
2021.6
考点
学习目标
核心素养
众数、中位数、平均数
会求样本的众数、中位数、平均数
数学抽象
总体集中趋势的估计
会用众数、中位数、平均数估计总体集中趋势
数据分析
你还记得平均数、中位数、众数是什么吗?这些统计量刻画了数据
的什么特点?
1.
众数、中位数、平均数的定义
⑴众数:在一组数据中,出现次数最多的数据叫做这组数据的众数.
⑵中位数:将一组数据按大小依次排列,把处在最中间位置的一个数据(或最中间两个数据的平均数)叫做这组数据的中位数.
⑶平均数:一组数据的算术平均数,即
?
x=
(x1+x2+…+xn)
1
n
如1
,2,3,3,3,5,5,8,8,8,9,9
如1
,2,3,3,3,5,5,8,8,8,9,9中位数是5
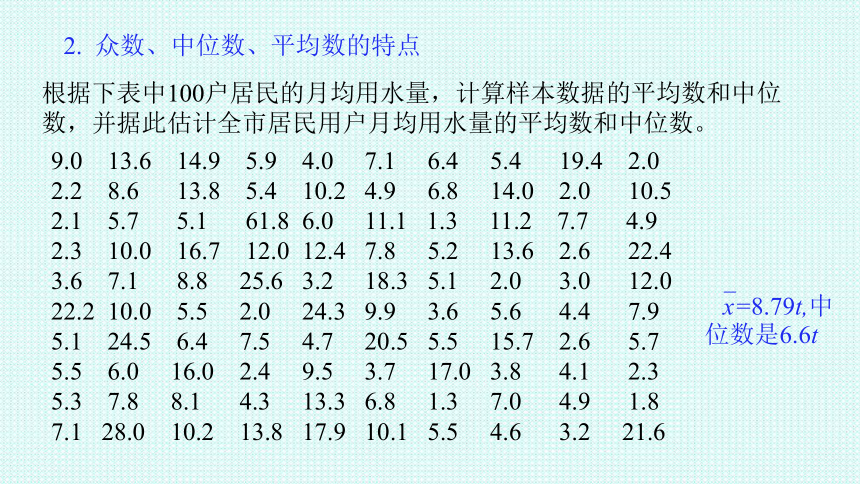
根据下表中100户居民的月均用水量,计算样本数据的平均数和中位数,并据此估计全市居民用户月均用水量的平均数和中位数。
9.0
13.6
14.9
5.9
4.0
7.1
6.4
5.4
19.4
2.0
2.2
8.6
13.8
5.4
10.2
4.9
6.8
14.0
2.0
10.5
2.1
5.7
5.1
61.8
6.0
11.1
1.3
11.2
7.7
4.9
2.3
10.0
16.7
12.0
12.4
7.8
5.2
13.6
2.6
22.4
3.6
7.1
8.8
25.6
3.2
18.3
5.1
2.0
3.0
12.0
22.2
10.0
5.5
2.0
24.3
9.9
3.6
5.6
4.4
7.9
5.1
24.5
6.4
7.5
4.7
20.5
5.5
15.7
2.6
5.7
5.5
6.0
16.0
2.4
9.5
3.7
17.0
3.8
4.1
2.3
5.3
7.8
8.1
4.3
13.3
6.8
1.3
7.0
4.9
1.8
7.1
28.0
10.2
13.8
17.9
10.1
5.5
4.6
3.2
21.6
?
x=8.79t,中
位数是6.6t
2.
众数、中位数、平均数的特点
(1).工作人员用统计软件计算了100户居民用水量的平均数和中位数。但在
录入数据时,不小心把一个数据7.7录成了77.请计算录入数据的平均数和
中位数。
通过简单计算发现,平均数由原来的8.79t变为9.483t,中位数没有变化,还是6.6t。
样本平均数与每一个样本数据有关,样本中的任何一个数据的改变都会引起平均数的改变.
中位数只利用了样本数据中间位置的一个或两个值,并未利用其他数据,所以不是任何一个样本数据的改变都会引起中位数的改变.
与中位数比较,平均数反映出样本数据中的更多信息,对样本中的极端值更加敏感.
众数只能告诉我们它比其他值出现的次数多,但并未告诉我们它比别的数值多的程度.
众数、中位数、平均数的意义
(1)样本的众数、中位数和平均数常用来表示样本数据的“中心值”,其中众数和中位数容易计算,不受少数几个极端值的影响,但只能表达样本数据中的少量信息,平均数代表了数据更多的信息,但受样本中每个数据的影响,越极端的数据对平均数的影响也越大;
(2)当一组数据中有不少数据重复出现时,其众数往往更能反映问题,当一组数据中个别数据较大时,可用中位数描述其集中趋势.
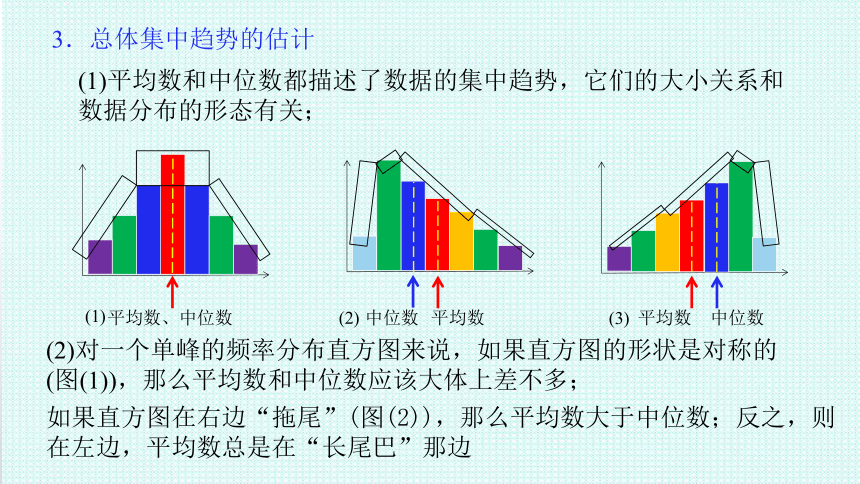
3.总体集中趋势的估计
(1)平均数和中位数都描述了数据的集中趋势,它们的大小关系和数据分布的形态有关;
平均数、中位数
中位数
平均数
平均数
中位数
(1)
(2)
(3)
(2)对一个单峰的频率分布直方图来说,如果直方图的形状是对称的(图(1)),那么平均数和中位数应该大体上差不多;
如果直方图在右边“拖尾”(图(2)),那么平均数大于中位数;反之,则
在左边,平均数总是在“长尾巴”那边
频率分布直方图中平均数、中位数、众数的求法
(1)平均数的估计
月均用水量/t
频率/组距
0.02
1.2
4.2
7.2
10.2
13.2
16.2
19.2
22.2
25.2
28.2
0
0.04
0.06
0.08
0.1
0.12
0.077
0.107
0.043
0.030
0.030
0.017
0.010
0.013
0.007
可以从频率分布直方图中估计平均数。平均数是频率分布直方图的“重心”等于频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之和。
小长方形面积
底边中点的横坐标
(2)中位数的估计
月均用水量/t
频率/组距
0.02
1.2
4.2
7.2
10.2
13.2
16.2
19.2
22.2
25.2
28.2
0
0.04
0.06
0.08
0.1
0.12
0.077
0.107
0.043
0.030
0.030
0.017
0.010
0.013
0.007
在频率分布直方图中,中位数左边和右边的直方图的面积各为0.5,
即在直方图中位数左右的面积相等.
(3)众数的估计
月均用水量/t
频率/组距
0.02
1.2
4.2
7.2
10.2
13.2
16.2
19.2
22.2
25.2
28.2
0
0.04
0.06
0.08
0.1
0.12
0.077
0.107
0.043
0.030
0.030
0.017
0.010
0.013
0.007
众数在样本数据的频率分布直方图中,
就是最高矩形的中点的横坐标.
用频率分布直方图估计众数、中位数、平均数
(1)众数:取最高小长方形底边中点的横坐标作为众数;
(2)中位数:在频率分布直方图中,把频率分布直方图划分
为左右两个面积相等的部分的分界线与x轴交点的横坐标称为中位数;
(3)平均数:平均数是频率分布直方图的“重心”,等于频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之和.
1.在一次体育测试中,某班的6名同学的成绩(单位:分)分别为66,83,87,
83,77,96.关于这组数据,下列说法错误的是
A.众数是83
B.中位数是83
C.极差是30
D.平均数是83
解析 由于83出现的次数最多,所以众数是83,故A说法正确;
把数据66,83,87,83,77,96按从小到大排列为66,77,83,83,87,96,中间两个数为83,83,所以中位数是83,故B说法正确;
极差是96-66=30,故C说法正确;
由于平均数为(66+83+87+83+77+96)÷6=82,故D说法错误,故选D.
2.下列关于平均数、中位数、众数的说法中正确的是
A.中位数可以准确地反映出总体的情况
B.平均数可以准确地反映出总体的情况
C.众数可以准确地反映出总体的情况
D.平均数、中位数、众数都有局限性,都不能准确地反映出总体的情况
3.某校高二年级有50人参加2020“希望杯”数学竞赛,他们竞赛的成绩制成了如下的频率分布表,根据该表估计该校学生数学竞赛成绩的平均分为( )
分组
[60,70)
[70,80)
[80,90)
[90,100]
频率
0.2
0.4
0.3
0.1
A.70
B.73
C.78
D.81.5
4.某工厂对一批新产品的长度(单位:mm)进行检测,如图是检测结果的频率分布直方图,据此估计这批产品的中位数为( )
A.20
B.25
C.22.5
D.22.75
10
15
20
25
长度/mm
频率/组距
30
35
0.02
0.03
0.04
0.08
自左至右各小矩形的面积依次为0.1,0.2,0.4,0.15,0.15,设中位数是x,则由0.1+0.2+0.08×(x-20)=0.5,得x=22.5.
5.(2021山东省泰安实验中学高一期中)在某次高中学科竞赛中,4000名考生的参赛成绩统计如图所示,60分以下视为不及格,若同一组中的数据用该组区间中点值为代表,则下列说法中不正确的是(
)
A.成绩在[70,80)分的考生人数最多
B.不及格的考生人数为1000
C.考生竞赛成绩的平均分约为70.5分
D.考生竞赛成绩的中位数为75分
40
50
60
70
成绩
频率/组距
80
90
100
0.010
0.015
0.020
0.030
[70,80)分频率最高,考生最多,
[40,60)为不及格,0.25×4000=1000,
45×0.1+55×0.15+65×0.2+75×0.3+85×0.15+95×0.1=70.5
6.已知一组数据丢失了其中一个,剩下的六个数据分别是3,3,5,3,6,11,若这组数据的平均数与众数的和是中位数的2倍,则丢失数据的所有可能值的和为( )
A.6
B.8
C.12
D.14
总体集中趋势的估计
安徽淮南第四中学
2021.6
考点
学习目标
核心素养
众数、中位数、平均数
会求样本的众数、中位数、平均数
数学抽象
总体集中趋势的估计
会用众数、中位数、平均数估计总体集中趋势
数据分析
你还记得平均数、中位数、众数是什么吗?这些统计量刻画了数据
的什么特点?
1.
众数、中位数、平均数的定义
⑴众数:在一组数据中,出现次数最多的数据叫做这组数据的众数.
⑵中位数:将一组数据按大小依次排列,把处在最中间位置的一个数据(或最中间两个数据的平均数)叫做这组数据的中位数.
⑶平均数:一组数据的算术平均数,即
?
x=
(x1+x2+…+xn)
1
n
如1
,2,3,3,3,5,5,8,8,8,9,9
如1
,2,3,3,3,5,5,8,8,8,9,9中位数是5
根据下表中100户居民的月均用水量,计算样本数据的平均数和中位数,并据此估计全市居民用户月均用水量的平均数和中位数。
9.0
13.6
14.9
5.9
4.0
7.1
6.4
5.4
19.4
2.0
2.2
8.6
13.8
5.4
10.2
4.9
6.8
14.0
2.0
10.5
2.1
5.7
5.1
61.8
6.0
11.1
1.3
11.2
7.7
4.9
2.3
10.0
16.7
12.0
12.4
7.8
5.2
13.6
2.6
22.4
3.6
7.1
8.8
25.6
3.2
18.3
5.1
2.0
3.0
12.0
22.2
10.0
5.5
2.0
24.3
9.9
3.6
5.6
4.4
7.9
5.1
24.5
6.4
7.5
4.7
20.5
5.5
15.7
2.6
5.7
5.5
6.0
16.0
2.4
9.5
3.7
17.0
3.8
4.1
2.3
5.3
7.8
8.1
4.3
13.3
6.8
1.3
7.0
4.9
1.8
7.1
28.0
10.2
13.8
17.9
10.1
5.5
4.6
3.2
21.6
?
x=8.79t,中
位数是6.6t
2.
众数、中位数、平均数的特点
(1).工作人员用统计软件计算了100户居民用水量的平均数和中位数。但在
录入数据时,不小心把一个数据7.7录成了77.请计算录入数据的平均数和
中位数。
通过简单计算发现,平均数由原来的8.79t变为9.483t,中位数没有变化,还是6.6t。
样本平均数与每一个样本数据有关,样本中的任何一个数据的改变都会引起平均数的改变.
中位数只利用了样本数据中间位置的一个或两个值,并未利用其他数据,所以不是任何一个样本数据的改变都会引起中位数的改变.
与中位数比较,平均数反映出样本数据中的更多信息,对样本中的极端值更加敏感.
众数只能告诉我们它比其他值出现的次数多,但并未告诉我们它比别的数值多的程度.
众数、中位数、平均数的意义
(1)样本的众数、中位数和平均数常用来表示样本数据的“中心值”,其中众数和中位数容易计算,不受少数几个极端值的影响,但只能表达样本数据中的少量信息,平均数代表了数据更多的信息,但受样本中每个数据的影响,越极端的数据对平均数的影响也越大;
(2)当一组数据中有不少数据重复出现时,其众数往往更能反映问题,当一组数据中个别数据较大时,可用中位数描述其集中趋势.
3.总体集中趋势的估计
(1)平均数和中位数都描述了数据的集中趋势,它们的大小关系和数据分布的形态有关;
平均数、中位数
中位数
平均数
平均数
中位数
(1)
(2)
(3)
(2)对一个单峰的频率分布直方图来说,如果直方图的形状是对称的(图(1)),那么平均数和中位数应该大体上差不多;
如果直方图在右边“拖尾”(图(2)),那么平均数大于中位数;反之,则
在左边,平均数总是在“长尾巴”那边
频率分布直方图中平均数、中位数、众数的求法
(1)平均数的估计
月均用水量/t
频率/组距
0.02
1.2
4.2
7.2
10.2
13.2
16.2
19.2
22.2
25.2
28.2
0
0.04
0.06
0.08
0.1
0.12
0.077
0.107
0.043
0.030
0.030
0.017
0.010
0.013
0.007
可以从频率分布直方图中估计平均数。平均数是频率分布直方图的“重心”等于频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之和。
小长方形面积
底边中点的横坐标
(2)中位数的估计
月均用水量/t
频率/组距
0.02
1.2
4.2
7.2
10.2
13.2
16.2
19.2
22.2
25.2
28.2
0
0.04
0.06
0.08
0.1
0.12
0.077
0.107
0.043
0.030
0.030
0.017
0.010
0.013
0.007
在频率分布直方图中,中位数左边和右边的直方图的面积各为0.5,
即在直方图中位数左右的面积相等.
(3)众数的估计
月均用水量/t
频率/组距
0.02
1.2
4.2
7.2
10.2
13.2
16.2
19.2
22.2
25.2
28.2
0
0.04
0.06
0.08
0.1
0.12
0.077
0.107
0.043
0.030
0.030
0.017
0.010
0.013
0.007
众数在样本数据的频率分布直方图中,
就是最高矩形的中点的横坐标.
用频率分布直方图估计众数、中位数、平均数
(1)众数:取最高小长方形底边中点的横坐标作为众数;
(2)中位数:在频率分布直方图中,把频率分布直方图划分
为左右两个面积相等的部分的分界线与x轴交点的横坐标称为中位数;
(3)平均数:平均数是频率分布直方图的“重心”,等于频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之和.
1.在一次体育测试中,某班的6名同学的成绩(单位:分)分别为66,83,87,
83,77,96.关于这组数据,下列说法错误的是
A.众数是83
B.中位数是83
C.极差是30
D.平均数是83
解析 由于83出现的次数最多,所以众数是83,故A说法正确;
把数据66,83,87,83,77,96按从小到大排列为66,77,83,83,87,96,中间两个数为83,83,所以中位数是83,故B说法正确;
极差是96-66=30,故C说法正确;
由于平均数为(66+83+87+83+77+96)÷6=82,故D说法错误,故选D.
2.下列关于平均数、中位数、众数的说法中正确的是
A.中位数可以准确地反映出总体的情况
B.平均数可以准确地反映出总体的情况
C.众数可以准确地反映出总体的情况
D.平均数、中位数、众数都有局限性,都不能准确地反映出总体的情况
3.某校高二年级有50人参加2020“希望杯”数学竞赛,他们竞赛的成绩制成了如下的频率分布表,根据该表估计该校学生数学竞赛成绩的平均分为( )
分组
[60,70)
[70,80)
[80,90)
[90,100]
频率
0.2
0.4
0.3
0.1
A.70
B.73
C.78
D.81.5
4.某工厂对一批新产品的长度(单位:mm)进行检测,如图是检测结果的频率分布直方图,据此估计这批产品的中位数为( )
A.20
B.25
C.22.5
D.22.75
10
15
20
25
长度/mm
频率/组距
30
35
0.02
0.03
0.04
0.08
自左至右各小矩形的面积依次为0.1,0.2,0.4,0.15,0.15,设中位数是x,则由0.1+0.2+0.08×(x-20)=0.5,得x=22.5.
5.(2021山东省泰安实验中学高一期中)在某次高中学科竞赛中,4000名考生的参赛成绩统计如图所示,60分以下视为不及格,若同一组中的数据用该组区间中点值为代表,则下列说法中不正确的是(
)
A.成绩在[70,80)分的考生人数最多
B.不及格的考生人数为1000
C.考生竞赛成绩的平均分约为70.5分
D.考生竞赛成绩的中位数为75分
40
50
60
70
成绩
频率/组距
80
90
100
0.010
0.015
0.020
0.030
[70,80)分频率最高,考生最多,
[40,60)为不及格,0.25×4000=1000,
45×0.1+55×0.15+65×0.2+75×0.3+85×0.15+95×0.1=70.5
6.已知一组数据丢失了其中一个,剩下的六个数据分别是3,3,5,3,6,11,若这组数据的平均数与众数的和是中位数的2倍,则丢失数据的所有可能值的和为( )
A.6
B.8
C.12
D.14
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
