2020-2021学年安徽省池州市东至县八年级(下)期末数学试卷 (word版含解析)
文档属性
| 名称 | 2020-2021学年安徽省池州市东至县八年级(下)期末数学试卷 (word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 972.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-29 07:04:34 | ||
图片预览




文档简介
2020-2021学年安徽省池州市东至县八年级(下)期末数学试卷
一、选择题(共10小题,每题3分,共30分).
1.计算×的结果是( )
A. B.4 C. D.2
2.与是同类二次根式的是( )
A. B. C. D.
3.若一个多边形的内角和等于1800度,则这个多边形是( )
A.十二边形 B.十边形 C.九边形 D.八边形
4.若关于x的一元二次方程x(x+1)+ax=0有两个相等的实数根,则实数a的值为( )
A.﹣1 B.1 C.﹣2或2 D.﹣3或1
5.某校初三66班学生毕业时,每个同学都要给其他同学写一份毕业留言作为纪念,全班学生共写了1640份留言,如果全班有x名学生,根据题意,列出方程为( )
A.=1640 B.=1640
C.x(x+1)=1640 D.x(x﹣1)=1640
6.某区“引进人才”招聘考试分笔试和面试.其中笔试按60%、面试按40%计算加权平均数作为总成绩.吴老师笔试成绩为90分.面试成绩为85分,那么吴老师的总成绩为( )分
A.85 B.86 C.87 D.88
7.?ABCD中,E,F是对角线BD上不同的两点.下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A.BE=DF B.AE=CF C.AF∥CE D.∠BAE=∠DCF
8.如图,△ABC中,DE∥BC,EF∥AB,要判定四边形DBFE是菱形,还需要添加的条件是( )
A.AB=AC B.AD=BD C.BE平分∠ABC D.BE⊥AC
9.如图,在四边形ABCD中,AC=BD=6,E、F、G、H分别是AB、BC、CD、DA的中点,则EG2+FH2的值为( )
A.9 B.18 C.36 D.48
10.如图,正方形ABCD的边长为4,点O是对角线BD的中点,点E、F分别在AB、AD边上运动,且保持BE=AF连接OE,OF,EF在此运动过程中,下列结论:①OE=OF;②∠EOF=90°;③四边形AEOF的面积保持不变;④当EF∥BD时,EF=2,其中正确的结论是( )
A.①② B.②③ C.①②④ D.①②③④
二、填空题(每小题3分,共24分)
11.要使有意义,则x的取值范围为 .
12.已知菱形ABCD的面积是12cm2,对角线AC=4cm,则菱形的边长是 cm.
13.在一次射击训练中,某位选手五次射击的环数分别为5,8,7,6,9,则这位选手五次射击环数的方差为 .
14.在实数范围内定义一种运算“*”,其规则为a*b=a2﹣b2,根据这个规则,方程(x+2)*5=0的解为 .
15.若关于x的方程(k﹣1)x2+4x+1=0有实数解,则k的取值范围是 .
16.如图所示,在平行四边形ABCD中,AB=5,BC=8,∠B=60°,E是BC的中点,EF⊥AB于点F,则△DEF的面积为 平方单位.
17.如图,已知菱形ABCD的周长为16,面积为8,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为 .
18.在平面直角坐标系中,点P(3,6),点O(0,0),点M在坐标轴上,当△POM是以PO为底的等腰三角形时,点M的坐标为 .
三、本题共4小趣,母小题8分,共16分
19.计算:﹣(+)(﹣).
20.解方程x2﹣1=4x.
四、本题共2小题,每小题8分,共16分
21.小明在解决问题,已知a=,求2a2﹣8a+1的值,他是这样分析与解答的:
∵a=;
∴a﹣2=﹣;
∴(a﹣2)2=3,即a2﹣4a+4=3;
∴a2﹣4a=﹣1;
∴2a2﹣8a+1=2(a2﹣4a)+1=2×(﹣1)+1=﹣1.
请你根据小明的分析过程,解决如下问题:
(1)计算:= ;
(2)若a=,求3a2﹣18a+5的值.
22.如图,正方形网格中的每个小正方形边长都为1,每个小正方形的顶点叫做格点,若Rt△DEF的三边长分别为m、n、d,满足=4n﹣n2﹣4,求三边长,若能画出以格点为顶点的三角形,请在图中画出该格点三角形.
五、本题满分10分
23.在“爱满扬州”慈善一日捐活动中,学校团总支为了了解本校学生的捐款情况,随机抽取了50名学生的捐款数进行了统计,并绘制成统计图.
(1)这50名同学捐款的众数为 元,中位数为 元;
(2)求这50名同学捐款的平均数;
(3)该校共有600名学生参与捐款,请估计该校学生的捐款总数.
六、本题满分12分
24.山清水秀的东至县三条岭已成为游客最喜欢的旅游地之一,其中“蔡岭”在2019年“五一”小长假期间,接待游客达2万人次,预计在2021年“五一”小长假期间,接待游客2.88万人次,在蔡岭,一家特色小面店希望在“五一”小长假期间获得好的收益,经测算知,该小面成本价为每碗10元,借鉴以往经验,若每碗卖15元,平均每天将销售120碗,若价格每提高0.5元,则平均每天少销售4碗,每天店面所需其他各种费用为168元.
(1)求出2019至2021年“五一”小长假期间游客人次的年平均增长率;
(2)为了更好地维护东至县形象,物价局规定每碗售价不得超过20元,则当每碗售价定为多少元时,店家才能实现每天净利润600元?(净利润=总收入﹣总成本﹣其它各种费用)
七、本题满分12分
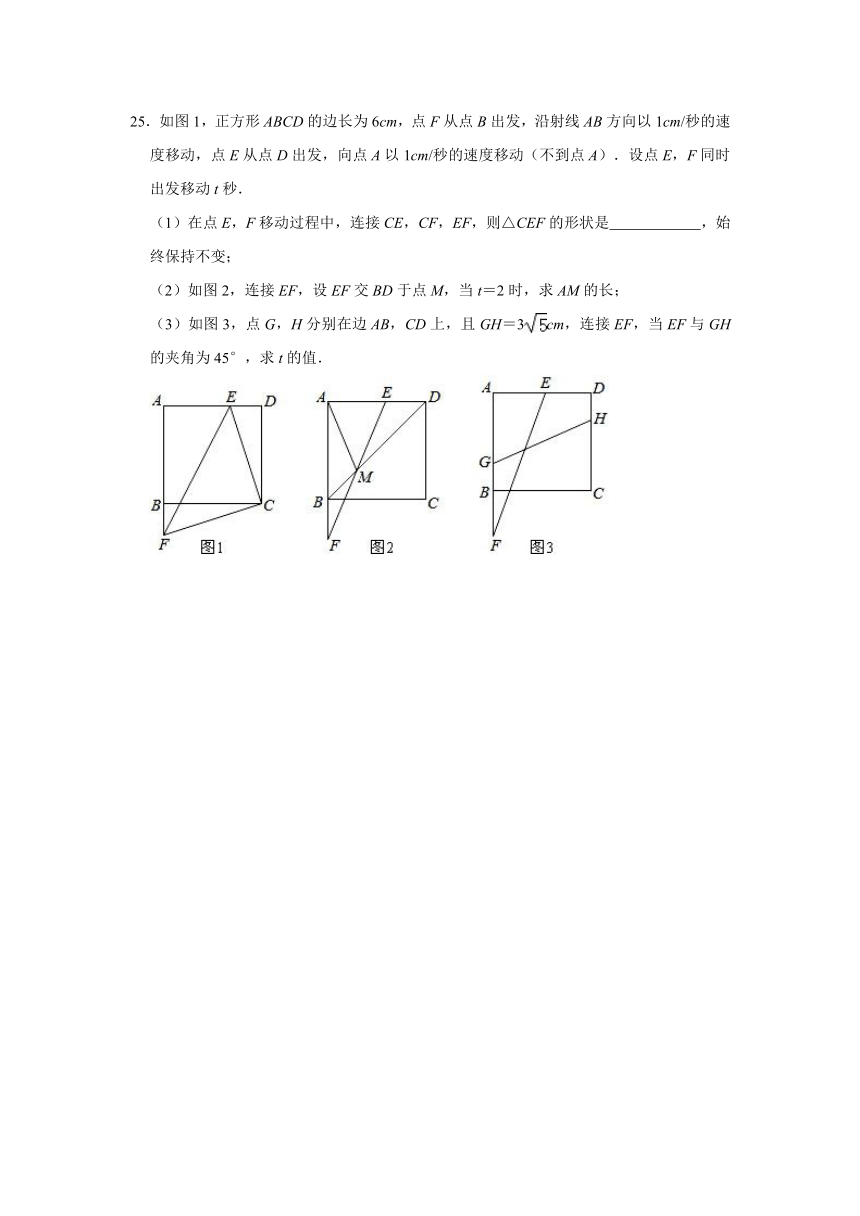
25.如图1,正方形ABCD的边长为6cm,点F从点B出发,沿射线AB方向以1cm/秒的速度移动,点E从点D出发,向点A以1cm/秒的速度移动(不到点A).设点E,F同时出发移动t秒.
(1)在点E,F移动过程中,连接CE,CF,EF,则△CEF的形状是 ,始终保持不变;
(2)如图2,连接EF,设EF交BD于点M,当t=2时,求AM的长;
(3)如图3,点G,H分别在边AB,CD上,且GH=3cm,连接EF,当EF与GH的夹角为45°,求t的值.
参考答案
一、选择题(每小题3分.共30分)
1.计算×的结果是( )
A. B.4 C. D.2
解:×==4.
故选:B.
2.与是同类二次根式的是( )
A. B. C. D.
解:=3,
A、=2,与不是同类二次根式;
B、=2,与不是同类二次根式;
C、=2,与是同类二次根式;
D、=3,与不是同类二次根式;
故选:C.
3.若一个多边形的内角和等于1800度,则这个多边形是( )
A.十二边形 B.十边形 C.九边形 D.八边形
解:设多边形的边数是n,则
(n﹣2)?180=1800,
解得n=12,
所以这个多边形是十二边形.
故选:A.
4.若关于x的一元二次方程x(x+1)+ax=0有两个相等的实数根,则实数a的值为( )
A.﹣1 B.1 C.﹣2或2 D.﹣3或1
解:原方程可变形为x2+(a+1)x=0.
∵该方程有两个相等的实数根,
∴△=(a+1)2﹣4×1×0=0,
解得:a=﹣1.
故选:A.
5.某校初三66班学生毕业时,每个同学都要给其他同学写一份毕业留言作为纪念,全班学生共写了1640份留言,如果全班有x名学生,根据题意,列出方程为( )
A.=1640 B.=1640
C.x(x+1)=1640 D.x(x﹣1)=1640
解:由题意可得,
x(x﹣1)=1640,
故选:D.
6.某区“引进人才”招聘考试分笔试和面试.其中笔试按60%、面试按40%计算加权平均数作为总成绩.吴老师笔试成绩为90分.面试成绩为85分,那么吴老师的总成绩为( )分
A.85 B.86 C.87 D.88
解:根据题意得,吴老师的综合成绩为90×60%+85×40%=88(分),
故选:D.
7.?ABCD中,E,F是对角线BD上不同的两点.下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A.BE=DF B.AE=CF C.AF∥CE D.∠BAE=∠DCF
解:如图,连接AC与BD相交于O,
在?ABCD中,OA=OC,OB=OD,
要使四边形AECF为平行四边形,只需证明得到OE=OF即可;
A、若BE=DF,则OB﹣BE=OD﹣DF,即OE=OF,故本选项不符合题意;
B、若AE=CF,则无法判断OE=OF,故本选项符合题意;
C、AF∥CE能够利用“角角边”证明△AOF和△COE全等,从而得到OE=OF,故本选项不符合题意;
D、∠BAE=∠DCF能够利用“角角边”证明△ABE和△CDF全等,从而得到DF=BE,然后同A,故本选项不符合题意;
故选:B.
8.如图,△ABC中,DE∥BC,EF∥AB,要判定四边形DBFE是菱形,还需要添加的条件是( )
A.AB=AC B.AD=BD C.BE平分∠ABC D.BE⊥AC
解:当BE平分∠ABC时,四边形DBFE是菱形,
理由:∵DE∥BC,
∴∠DEB=∠EBC,
∵∠EBC=∠EBD,
∴∠EBD=∠DEB,
∴BD=DE,
∵DE∥BC,EF∥AB,
∴四边形DBFE是平行四边形,
∵BD=DE,
∴四边形DBFE是菱形.
其余选项均无法判断四边形DBFE是菱形,
故选:C.
9.如图,在四边形ABCD中,AC=BD=6,E、F、G、H分别是AB、BC、CD、DA的中点,则EG2+FH2的值为( )
A.9 B.18 C.36 D.48
解:连接EF、FG、GH、EH,设EG和FH交于点O,
∵E、F、G、H分别是AB、BC、CD、DA的中点,
∴EF∥AC,HG∥AC,EF=AC,FG=BD,
∴EF∥HG,
同理EH∥FG,
∴四边形EFGH为平行四边形,
∵AC=BD,
∴EF=FG,
∴平行四边形EFGH为菱形,
∴EG⊥FH,EG=2OG,FH=2OH,
∴EG2+FH2=(2OE)2+(2OH)2=4(OE2+OH2)=4EH2=4×(BD)2=62=36;
故选:C.
10.如图,正方形ABCD的边长为4,点O是对角线BD的中点,点E、F分别在AB、AD边上运动,且保持BE=AF连接OE,OF,EF在此运动过程中,下列结论:①OE=OF;②∠EOF=90°;③四边形AEOF的面积保持不变;④当EF∥BD时,EF=2,其中正确的结论是( )
A.①② B.②③ C.①②④ D.①②③④
解:过O作OG⊥AB于G,OH⊥AD于H,
∵四边形ABCD是正方形,
∴∠A=∠OHA=∠OGA=90°,
OH∥AB,OG∥AD,
∵点O是对角线BD的中点,
∴AH=DH,AG=BG,
∴OH=AB,OG=AD,
∵AD=BA,
∴OG=OH,BG=AH,
∴四边形AGOH是正方形,
∴∠GOH=90°,
∵BE=AF,
∴GE=FH,
在△OFH与△OEG中,,
∴△OFH≌△OEG(SAS),
∴OE=OF,故①正确;∠EOG=∠FOH,
∴∠EOG+∠GOF=∠GOF+∠FOH=90°,
∴∠EOF=90°,故②正确;
∵△OFH≌△OEG,
∴四边形AEOF的面积=正方形AOGH的面积=2×2=4,
∴四边形AEOF的面积保持不变;故③正确;
∵EF∥BD,
∴∠AFE=∠ADB=45°,∠AEF=∠ABD=45°,
∴AE=AF,
∵BE=AF,
∴AE=BE,
∴AE=AF=AB=2,
∴EF=2,故④正确;
故选:D.
二、填空题(每小题3分,共24分)
11.要使有意义,则x的取值范围为 x≥3 .
解:由题意得,2x﹣6≥0,
解得x≥3.
故答案为:x≥3.
12.已知菱形ABCD的面积是12cm2,对角线AC=4cm,则菱形的边长是 cm.
解:由菱形的面积公式,可得另一对角线长12×2×=6,
∵菱形的对角线互相垂直平分,
根据勾股定理可得菱形的边长==cm.
故答案为.
13.在一次射击训练中,某位选手五次射击的环数分别为5,8,7,6,9,则这位选手五次射击环数的方差为 2 .
解:五次射击的平均成绩为=(5+7+8+6+9)=7,
方差S2=[(5﹣7)2+(8﹣7)2+(7﹣7)2+(6﹣7)2+(9﹣7)2]=2.
故答案为:2.
14.在实数范围内定义一种运算“*”,其规则为a*b=a2﹣b2,根据这个规则,方程(x+2)*5=0的解为 x=3或x=﹣7 .
解:据题意得,
∵(x+2)*5=(x+2)2﹣52
∴x2+4x﹣21=0,
∴(x﹣3)(x+7)=0,
∴x=3或x=﹣7.
故答案为:x=3或x=﹣7
15.若关于x的方程(k﹣1)x2+4x+1=0有实数解,则k的取值范围是 k≤5 .
解:当k﹣1=0时,方程为4x+1=0,显然有实数根;
当k﹣1≠0,即k≠1时,△=42﹣4×(k﹣1)×1≥0,
解得k≤5且k≠1;
综上,k≤5.
故答案为:k≤5.
16.如图所示,在平行四边形ABCD中,AB=5,BC=8,∠B=60°,E是BC的中点,EF⊥AB于点F,则△DEF的面积为 7 平方单位.
解:如图,延长DC和FE交于点G,
在平行四边形ABCD中,AB∥CD,
∴∠B=∠ECG,
∵E为BC的中点,
∴BE=CE=BC=×8=4,
在△BEF和△CEG中,
,
∴△BEF≌△CEG(ASA),
∴BF=CG,
∵∠B=60°,
∴∠FEB=30°,
∴BF=BE=2,
∴EF=2,
∵CG=BF=2,CD=AB=5,
∴DG=CD+CG=5+2=7,
∵EF⊥AB,AB∥CD,
∴DG⊥FG,
∴S△DEF=EF?DG=2×7=7,
故答案为:7.
17.如图,已知菱形ABCD的周长为16,面积为8,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为 2 .
解:如图,作CE′⊥AB于E′,交BD于P′,连接AC、AP′.
∵已知菱形ABCD的周长为16,面积为8,
∴AB=BC=4,AB?CE′=8,
∴CE′=2,
在Rt△BCE′中,BE′==2,
∵BE=EA=2,
∴E与E′重合,
∵四边形ABCD是菱形,
∴BD垂直平分AC,
∴A、C关于BD对称,
∴当P与P′重合时,P′A+P′E的值最小,最小值为CE=2,
故答案为:2.
18.在平面直角坐标系中,点P(3,6),点O(0,0),点M在坐标轴上,当△POM是以PO为底的等腰三角形时,点M的坐标为 (,0)或(0,) .
解:当M点在x轴上时,设M(a,0),
∵△POM是以PO为底的等腰三角形,
∴OM=PM,
∴a2=(a﹣3)2+62,
解得a=,
∴此时M为(,0),
当M点在x轴上时,设M(0,b),
∵△POM是以PO为底的等腰三角形,
∴OM=PM,
∴b2=32+(6﹣b)2,
解得b=,
∴此时M(0,),
综上,点M的坐标为(,0)或(0,),
故答案为(,0)或(0,).
三、本题共4小趣,母小题8分,共16分
19.计算:﹣(+)(﹣).
解:原式=2+2+3﹣(2﹣3)
=5+2+1
=6+2.
20.解方程x2﹣1=4x.
解:原方程化为一般式:x2﹣4x﹣1=0.
∵a=1,b=﹣4,c=﹣1,
∴△=b2﹣4ac=(﹣4)2﹣4×1×(﹣1)=20>0,
∴x===2±,
∴x1=2+,x2=2﹣.
四、本题共2小题,每小题8分,共16分
21.小明在解决问题,已知a=,求2a2﹣8a+1的值,他是这样分析与解答的:
∵a=;
∴a﹣2=﹣;
∴(a﹣2)2=3,即a2﹣4a+4=3;
∴a2﹣4a=﹣1;
∴2a2﹣8a+1=2(a2﹣4a)+1=2×(﹣1)+1=﹣1.
请你根据小明的分析过程,解决如下问题:
(1)计算:= ﹣ ;
(2)若a=,求3a2﹣18a+5的值.
解:(1)==﹣;
故答案为:﹣;
(2)∵a===+3,
∴3a2﹣18a+5
=3(a2﹣6a)+5
=3[(a﹣3)2﹣9]+5
=(a﹣3)2﹣22,
=(+3﹣3)2﹣22
=10﹣22
=﹣12.
22.如图,正方形网格中的每个小正方形边长都为1,每个小正方形的顶点叫做格点,若Rt△DEF的三边长分别为m、n、d,满足=4n﹣n2﹣4,求三边长,若能画出以格点为顶点的三角形,请在图中画出该格点三角形.
解:∵=4n﹣n2﹣4,
∴+(n﹣2)2=0,
∵≥0,(n﹣2)2≥0,
∴m=3,n=2,
∵Rt△DEF的三边长分别为m、n、d,
∴当m,n是直角边时,d==,
当m=3是斜边时,d==,
∴三边长为:2,3,或2,,3,
图形如图所示:
五、本题满分10分
23.在“爱满扬州”慈善一日捐活动中,学校团总支为了了解本校学生的捐款情况,随机抽取了50名学生的捐款数进行了统计,并绘制成统计图.
(1)这50名同学捐款的众数为 15 元,中位数为 15 元;
(2)求这50名同学捐款的平均数;
(3)该校共有600名学生参与捐款,请估计该校学生的捐款总数.
解:(1)数据15元出现了20次,出现次数最多,所以众数是15元;
数据总数为50,所以中位数是第25、26位数的平均数,即(15+15)÷2=15(元).
故答案为15,15;
(2)50名同学捐款的平均数=(5×8+10×14+15×20+20×6+25×2)÷50=13(元);
(3)估计这个中学的捐款总数=600×13=7800(元).
六、本题满分12分
24.山清水秀的东至县三条岭已成为游客最喜欢的旅游地之一,其中“蔡岭”在2019年“五一”小长假期间,接待游客达2万人次,预计在2021年“五一”小长假期间,接待游客2.88万人次,在蔡岭,一家特色小面店希望在“五一”小长假期间获得好的收益,经测算知,该小面成本价为每碗10元,借鉴以往经验,若每碗卖15元,平均每天将销售120碗,若价格每提高0.5元,则平均每天少销售4碗,每天店面所需其他各种费用为168元.
(1)求出2019至2021年“五一”小长假期间游客人次的年平均增长率;
(2)为了更好地维护东至县形象,物价局规定每碗售价不得超过20元,则当每碗售价定为多少元时,店家才能实现每天净利润600元?(净利润=总收入﹣总成本﹣其它各种费用)
解:(1)可设年平均增长率为x,依题意有
2(1+x)2=2.88,
解得x1=0.2=20%,x2=﹣2.2(舍去).
答:年平均增长率为20%;
(2)设每碗售价定为y元时,店家才能实现每天利润600元,依题意得:
(y﹣10)[120﹣(y﹣15)]﹣168=600,
解得y1=18,y2=22,
∵每碗售价不得超过20元,
∴y=18.
答:当每碗售价定为18元时,店家才能实现每天利润600元.
七、本题满分12分
25.如图1,正方形ABCD的边长为6cm,点F从点B出发,沿射线AB方向以1cm/秒的速度移动,点E从点D出发,向点A以1cm/秒的速度移动(不到点A).设点E,F同时出发移动t秒.
(1)在点E,F移动过程中,连接CE,CF,EF,则△CEF的形状是 等腰直角三角形 ,始终保持不变;
(2)如图2,连接EF,设EF交BD于点M,当t=2时,求AM的长;
(3)如图3,点G,H分别在边AB,CD上,且GH=3cm,连接EF,当EF与GH的夹角为45°,求t的值.
解:(1)等腰直角三角形.理由如下:
如图1,在正方形ABCD中,DC=BC,∠D=∠ABC=90°.
依题意得:DE=BF=t.
在△CDE与△CBF中,
,
∴△CDE≌△CBF(SAS),
∴CF=CE,∠DCE=∠BCF,
∴∠ECF=∠BCF+∠BCE=∠DCE+∠BCE=∠BCD=90°,
∴△CEF是等腰直角三角形.
故答案是:等腰直角三角形.
(2)如图2,过点E作EN∥AB,交BD于点N,则∠NEM=∠BFM.
∴∠END=∠ABD=∠EDN=45°,
∴EN=ED=BF.
在△EMN与△FMB中,
,
∴△EMN≌△FMB(AAS),
∴EM=FM.
∵Rt△AEF中,AE=4,AF=8,
∴=EF==4,
∴AM=EF=2;
(3)如图3,连接CE,CF,EF与GH交于P.
由(1)得∠CFE=45°,又∠EPQ=45°,
∴GH∥CF,
又∵AF∥DC,
∴四边形GFCH是平行四边形,
∴CF=GH=3,
在Rt△CBF中,得BF===3,
∴t=3.
一、选择题(共10小题,每题3分,共30分).
1.计算×的结果是( )
A. B.4 C. D.2
2.与是同类二次根式的是( )
A. B. C. D.
3.若一个多边形的内角和等于1800度,则这个多边形是( )
A.十二边形 B.十边形 C.九边形 D.八边形
4.若关于x的一元二次方程x(x+1)+ax=0有两个相等的实数根,则实数a的值为( )
A.﹣1 B.1 C.﹣2或2 D.﹣3或1
5.某校初三66班学生毕业时,每个同学都要给其他同学写一份毕业留言作为纪念,全班学生共写了1640份留言,如果全班有x名学生,根据题意,列出方程为( )
A.=1640 B.=1640
C.x(x+1)=1640 D.x(x﹣1)=1640
6.某区“引进人才”招聘考试分笔试和面试.其中笔试按60%、面试按40%计算加权平均数作为总成绩.吴老师笔试成绩为90分.面试成绩为85分,那么吴老师的总成绩为( )分
A.85 B.86 C.87 D.88
7.?ABCD中,E,F是对角线BD上不同的两点.下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A.BE=DF B.AE=CF C.AF∥CE D.∠BAE=∠DCF
8.如图,△ABC中,DE∥BC,EF∥AB,要判定四边形DBFE是菱形,还需要添加的条件是( )
A.AB=AC B.AD=BD C.BE平分∠ABC D.BE⊥AC
9.如图,在四边形ABCD中,AC=BD=6,E、F、G、H分别是AB、BC、CD、DA的中点,则EG2+FH2的值为( )
A.9 B.18 C.36 D.48
10.如图,正方形ABCD的边长为4,点O是对角线BD的中点,点E、F分别在AB、AD边上运动,且保持BE=AF连接OE,OF,EF在此运动过程中,下列结论:①OE=OF;②∠EOF=90°;③四边形AEOF的面积保持不变;④当EF∥BD时,EF=2,其中正确的结论是( )
A.①② B.②③ C.①②④ D.①②③④
二、填空题(每小题3分,共24分)
11.要使有意义,则x的取值范围为 .
12.已知菱形ABCD的面积是12cm2,对角线AC=4cm,则菱形的边长是 cm.
13.在一次射击训练中,某位选手五次射击的环数分别为5,8,7,6,9,则这位选手五次射击环数的方差为 .
14.在实数范围内定义一种运算“*”,其规则为a*b=a2﹣b2,根据这个规则,方程(x+2)*5=0的解为 .
15.若关于x的方程(k﹣1)x2+4x+1=0有实数解,则k的取值范围是 .
16.如图所示,在平行四边形ABCD中,AB=5,BC=8,∠B=60°,E是BC的中点,EF⊥AB于点F,则△DEF的面积为 平方单位.
17.如图,已知菱形ABCD的周长为16,面积为8,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为 .
18.在平面直角坐标系中,点P(3,6),点O(0,0),点M在坐标轴上,当△POM是以PO为底的等腰三角形时,点M的坐标为 .
三、本题共4小趣,母小题8分,共16分
19.计算:﹣(+)(﹣).
20.解方程x2﹣1=4x.
四、本题共2小题,每小题8分,共16分
21.小明在解决问题,已知a=,求2a2﹣8a+1的值,他是这样分析与解答的:
∵a=;
∴a﹣2=﹣;
∴(a﹣2)2=3,即a2﹣4a+4=3;
∴a2﹣4a=﹣1;
∴2a2﹣8a+1=2(a2﹣4a)+1=2×(﹣1)+1=﹣1.
请你根据小明的分析过程,解决如下问题:
(1)计算:= ;
(2)若a=,求3a2﹣18a+5的值.
22.如图,正方形网格中的每个小正方形边长都为1,每个小正方形的顶点叫做格点,若Rt△DEF的三边长分别为m、n、d,满足=4n﹣n2﹣4,求三边长,若能画出以格点为顶点的三角形,请在图中画出该格点三角形.
五、本题满分10分
23.在“爱满扬州”慈善一日捐活动中,学校团总支为了了解本校学生的捐款情况,随机抽取了50名学生的捐款数进行了统计,并绘制成统计图.
(1)这50名同学捐款的众数为 元,中位数为 元;
(2)求这50名同学捐款的平均数;
(3)该校共有600名学生参与捐款,请估计该校学生的捐款总数.
六、本题满分12分
24.山清水秀的东至县三条岭已成为游客最喜欢的旅游地之一,其中“蔡岭”在2019年“五一”小长假期间,接待游客达2万人次,预计在2021年“五一”小长假期间,接待游客2.88万人次,在蔡岭,一家特色小面店希望在“五一”小长假期间获得好的收益,经测算知,该小面成本价为每碗10元,借鉴以往经验,若每碗卖15元,平均每天将销售120碗,若价格每提高0.5元,则平均每天少销售4碗,每天店面所需其他各种费用为168元.
(1)求出2019至2021年“五一”小长假期间游客人次的年平均增长率;
(2)为了更好地维护东至县形象,物价局规定每碗售价不得超过20元,则当每碗售价定为多少元时,店家才能实现每天净利润600元?(净利润=总收入﹣总成本﹣其它各种费用)
七、本题满分12分
25.如图1,正方形ABCD的边长为6cm,点F从点B出发,沿射线AB方向以1cm/秒的速度移动,点E从点D出发,向点A以1cm/秒的速度移动(不到点A).设点E,F同时出发移动t秒.
(1)在点E,F移动过程中,连接CE,CF,EF,则△CEF的形状是 ,始终保持不变;
(2)如图2,连接EF,设EF交BD于点M,当t=2时,求AM的长;
(3)如图3,点G,H分别在边AB,CD上,且GH=3cm,连接EF,当EF与GH的夹角为45°,求t的值.
参考答案
一、选择题(每小题3分.共30分)
1.计算×的结果是( )
A. B.4 C. D.2
解:×==4.
故选:B.
2.与是同类二次根式的是( )
A. B. C. D.
解:=3,
A、=2,与不是同类二次根式;
B、=2,与不是同类二次根式;
C、=2,与是同类二次根式;
D、=3,与不是同类二次根式;
故选:C.
3.若一个多边形的内角和等于1800度,则这个多边形是( )
A.十二边形 B.十边形 C.九边形 D.八边形
解:设多边形的边数是n,则
(n﹣2)?180=1800,
解得n=12,
所以这个多边形是十二边形.
故选:A.
4.若关于x的一元二次方程x(x+1)+ax=0有两个相等的实数根,则实数a的值为( )
A.﹣1 B.1 C.﹣2或2 D.﹣3或1
解:原方程可变形为x2+(a+1)x=0.
∵该方程有两个相等的实数根,
∴△=(a+1)2﹣4×1×0=0,
解得:a=﹣1.
故选:A.
5.某校初三66班学生毕业时,每个同学都要给其他同学写一份毕业留言作为纪念,全班学生共写了1640份留言,如果全班有x名学生,根据题意,列出方程为( )
A.=1640 B.=1640
C.x(x+1)=1640 D.x(x﹣1)=1640
解:由题意可得,
x(x﹣1)=1640,
故选:D.
6.某区“引进人才”招聘考试分笔试和面试.其中笔试按60%、面试按40%计算加权平均数作为总成绩.吴老师笔试成绩为90分.面试成绩为85分,那么吴老师的总成绩为( )分
A.85 B.86 C.87 D.88
解:根据题意得,吴老师的综合成绩为90×60%+85×40%=88(分),
故选:D.
7.?ABCD中,E,F是对角线BD上不同的两点.下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A.BE=DF B.AE=CF C.AF∥CE D.∠BAE=∠DCF
解:如图,连接AC与BD相交于O,
在?ABCD中,OA=OC,OB=OD,
要使四边形AECF为平行四边形,只需证明得到OE=OF即可;
A、若BE=DF,则OB﹣BE=OD﹣DF,即OE=OF,故本选项不符合题意;
B、若AE=CF,则无法判断OE=OF,故本选项符合题意;
C、AF∥CE能够利用“角角边”证明△AOF和△COE全等,从而得到OE=OF,故本选项不符合题意;
D、∠BAE=∠DCF能够利用“角角边”证明△ABE和△CDF全等,从而得到DF=BE,然后同A,故本选项不符合题意;
故选:B.
8.如图,△ABC中,DE∥BC,EF∥AB,要判定四边形DBFE是菱形,还需要添加的条件是( )
A.AB=AC B.AD=BD C.BE平分∠ABC D.BE⊥AC
解:当BE平分∠ABC时,四边形DBFE是菱形,
理由:∵DE∥BC,
∴∠DEB=∠EBC,
∵∠EBC=∠EBD,
∴∠EBD=∠DEB,
∴BD=DE,
∵DE∥BC,EF∥AB,
∴四边形DBFE是平行四边形,
∵BD=DE,
∴四边形DBFE是菱形.
其余选项均无法判断四边形DBFE是菱形,
故选:C.
9.如图,在四边形ABCD中,AC=BD=6,E、F、G、H分别是AB、BC、CD、DA的中点,则EG2+FH2的值为( )
A.9 B.18 C.36 D.48
解:连接EF、FG、GH、EH,设EG和FH交于点O,
∵E、F、G、H分别是AB、BC、CD、DA的中点,
∴EF∥AC,HG∥AC,EF=AC,FG=BD,
∴EF∥HG,
同理EH∥FG,
∴四边形EFGH为平行四边形,
∵AC=BD,
∴EF=FG,
∴平行四边形EFGH为菱形,
∴EG⊥FH,EG=2OG,FH=2OH,
∴EG2+FH2=(2OE)2+(2OH)2=4(OE2+OH2)=4EH2=4×(BD)2=62=36;
故选:C.
10.如图,正方形ABCD的边长为4,点O是对角线BD的中点,点E、F分别在AB、AD边上运动,且保持BE=AF连接OE,OF,EF在此运动过程中,下列结论:①OE=OF;②∠EOF=90°;③四边形AEOF的面积保持不变;④当EF∥BD时,EF=2,其中正确的结论是( )
A.①② B.②③ C.①②④ D.①②③④
解:过O作OG⊥AB于G,OH⊥AD于H,
∵四边形ABCD是正方形,
∴∠A=∠OHA=∠OGA=90°,
OH∥AB,OG∥AD,
∵点O是对角线BD的中点,
∴AH=DH,AG=BG,
∴OH=AB,OG=AD,
∵AD=BA,
∴OG=OH,BG=AH,
∴四边形AGOH是正方形,
∴∠GOH=90°,
∵BE=AF,
∴GE=FH,
在△OFH与△OEG中,,
∴△OFH≌△OEG(SAS),
∴OE=OF,故①正确;∠EOG=∠FOH,
∴∠EOG+∠GOF=∠GOF+∠FOH=90°,
∴∠EOF=90°,故②正确;
∵△OFH≌△OEG,
∴四边形AEOF的面积=正方形AOGH的面积=2×2=4,
∴四边形AEOF的面积保持不变;故③正确;
∵EF∥BD,
∴∠AFE=∠ADB=45°,∠AEF=∠ABD=45°,
∴AE=AF,
∵BE=AF,
∴AE=BE,
∴AE=AF=AB=2,
∴EF=2,故④正确;
故选:D.
二、填空题(每小题3分,共24分)
11.要使有意义,则x的取值范围为 x≥3 .
解:由题意得,2x﹣6≥0,
解得x≥3.
故答案为:x≥3.
12.已知菱形ABCD的面积是12cm2,对角线AC=4cm,则菱形的边长是 cm.
解:由菱形的面积公式,可得另一对角线长12×2×=6,
∵菱形的对角线互相垂直平分,
根据勾股定理可得菱形的边长==cm.
故答案为.
13.在一次射击训练中,某位选手五次射击的环数分别为5,8,7,6,9,则这位选手五次射击环数的方差为 2 .
解:五次射击的平均成绩为=(5+7+8+6+9)=7,
方差S2=[(5﹣7)2+(8﹣7)2+(7﹣7)2+(6﹣7)2+(9﹣7)2]=2.
故答案为:2.
14.在实数范围内定义一种运算“*”,其规则为a*b=a2﹣b2,根据这个规则,方程(x+2)*5=0的解为 x=3或x=﹣7 .
解:据题意得,
∵(x+2)*5=(x+2)2﹣52
∴x2+4x﹣21=0,
∴(x﹣3)(x+7)=0,
∴x=3或x=﹣7.
故答案为:x=3或x=﹣7
15.若关于x的方程(k﹣1)x2+4x+1=0有实数解,则k的取值范围是 k≤5 .
解:当k﹣1=0时,方程为4x+1=0,显然有实数根;
当k﹣1≠0,即k≠1时,△=42﹣4×(k﹣1)×1≥0,
解得k≤5且k≠1;
综上,k≤5.
故答案为:k≤5.
16.如图所示,在平行四边形ABCD中,AB=5,BC=8,∠B=60°,E是BC的中点,EF⊥AB于点F,则△DEF的面积为 7 平方单位.
解:如图,延长DC和FE交于点G,
在平行四边形ABCD中,AB∥CD,
∴∠B=∠ECG,
∵E为BC的中点,
∴BE=CE=BC=×8=4,
在△BEF和△CEG中,
,
∴△BEF≌△CEG(ASA),
∴BF=CG,
∵∠B=60°,
∴∠FEB=30°,
∴BF=BE=2,
∴EF=2,
∵CG=BF=2,CD=AB=5,
∴DG=CD+CG=5+2=7,
∵EF⊥AB,AB∥CD,
∴DG⊥FG,
∴S△DEF=EF?DG=2×7=7,
故答案为:7.
17.如图,已知菱形ABCD的周长为16,面积为8,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为 2 .
解:如图,作CE′⊥AB于E′,交BD于P′,连接AC、AP′.
∵已知菱形ABCD的周长为16,面积为8,
∴AB=BC=4,AB?CE′=8,
∴CE′=2,
在Rt△BCE′中,BE′==2,
∵BE=EA=2,
∴E与E′重合,
∵四边形ABCD是菱形,
∴BD垂直平分AC,
∴A、C关于BD对称,
∴当P与P′重合时,P′A+P′E的值最小,最小值为CE=2,
故答案为:2.
18.在平面直角坐标系中,点P(3,6),点O(0,0),点M在坐标轴上,当△POM是以PO为底的等腰三角形时,点M的坐标为 (,0)或(0,) .
解:当M点在x轴上时,设M(a,0),
∵△POM是以PO为底的等腰三角形,
∴OM=PM,
∴a2=(a﹣3)2+62,
解得a=,
∴此时M为(,0),
当M点在x轴上时,设M(0,b),
∵△POM是以PO为底的等腰三角形,
∴OM=PM,
∴b2=32+(6﹣b)2,
解得b=,
∴此时M(0,),
综上,点M的坐标为(,0)或(0,),
故答案为(,0)或(0,).
三、本题共4小趣,母小题8分,共16分
19.计算:﹣(+)(﹣).
解:原式=2+2+3﹣(2﹣3)
=5+2+1
=6+2.
20.解方程x2﹣1=4x.
解:原方程化为一般式:x2﹣4x﹣1=0.
∵a=1,b=﹣4,c=﹣1,
∴△=b2﹣4ac=(﹣4)2﹣4×1×(﹣1)=20>0,
∴x===2±,
∴x1=2+,x2=2﹣.
四、本题共2小题,每小题8分,共16分
21.小明在解决问题,已知a=,求2a2﹣8a+1的值,他是这样分析与解答的:
∵a=;
∴a﹣2=﹣;
∴(a﹣2)2=3,即a2﹣4a+4=3;
∴a2﹣4a=﹣1;
∴2a2﹣8a+1=2(a2﹣4a)+1=2×(﹣1)+1=﹣1.
请你根据小明的分析过程,解决如下问题:
(1)计算:= ﹣ ;
(2)若a=,求3a2﹣18a+5的值.
解:(1)==﹣;
故答案为:﹣;
(2)∵a===+3,
∴3a2﹣18a+5
=3(a2﹣6a)+5
=3[(a﹣3)2﹣9]+5
=(a﹣3)2﹣22,
=(+3﹣3)2﹣22
=10﹣22
=﹣12.
22.如图,正方形网格中的每个小正方形边长都为1,每个小正方形的顶点叫做格点,若Rt△DEF的三边长分别为m、n、d,满足=4n﹣n2﹣4,求三边长,若能画出以格点为顶点的三角形,请在图中画出该格点三角形.
解:∵=4n﹣n2﹣4,
∴+(n﹣2)2=0,
∵≥0,(n﹣2)2≥0,
∴m=3,n=2,
∵Rt△DEF的三边长分别为m、n、d,
∴当m,n是直角边时,d==,
当m=3是斜边时,d==,
∴三边长为:2,3,或2,,3,
图形如图所示:
五、本题满分10分
23.在“爱满扬州”慈善一日捐活动中,学校团总支为了了解本校学生的捐款情况,随机抽取了50名学生的捐款数进行了统计,并绘制成统计图.
(1)这50名同学捐款的众数为 15 元,中位数为 15 元;
(2)求这50名同学捐款的平均数;
(3)该校共有600名学生参与捐款,请估计该校学生的捐款总数.
解:(1)数据15元出现了20次,出现次数最多,所以众数是15元;
数据总数为50,所以中位数是第25、26位数的平均数,即(15+15)÷2=15(元).
故答案为15,15;
(2)50名同学捐款的平均数=(5×8+10×14+15×20+20×6+25×2)÷50=13(元);
(3)估计这个中学的捐款总数=600×13=7800(元).
六、本题满分12分
24.山清水秀的东至县三条岭已成为游客最喜欢的旅游地之一,其中“蔡岭”在2019年“五一”小长假期间,接待游客达2万人次,预计在2021年“五一”小长假期间,接待游客2.88万人次,在蔡岭,一家特色小面店希望在“五一”小长假期间获得好的收益,经测算知,该小面成本价为每碗10元,借鉴以往经验,若每碗卖15元,平均每天将销售120碗,若价格每提高0.5元,则平均每天少销售4碗,每天店面所需其他各种费用为168元.
(1)求出2019至2021年“五一”小长假期间游客人次的年平均增长率;
(2)为了更好地维护东至县形象,物价局规定每碗售价不得超过20元,则当每碗售价定为多少元时,店家才能实现每天净利润600元?(净利润=总收入﹣总成本﹣其它各种费用)
解:(1)可设年平均增长率为x,依题意有
2(1+x)2=2.88,
解得x1=0.2=20%,x2=﹣2.2(舍去).
答:年平均增长率为20%;
(2)设每碗售价定为y元时,店家才能实现每天利润600元,依题意得:
(y﹣10)[120﹣(y﹣15)]﹣168=600,
解得y1=18,y2=22,
∵每碗售价不得超过20元,
∴y=18.
答:当每碗售价定为18元时,店家才能实现每天利润600元.
七、本题满分12分
25.如图1,正方形ABCD的边长为6cm,点F从点B出发,沿射线AB方向以1cm/秒的速度移动,点E从点D出发,向点A以1cm/秒的速度移动(不到点A).设点E,F同时出发移动t秒.
(1)在点E,F移动过程中,连接CE,CF,EF,则△CEF的形状是 等腰直角三角形 ,始终保持不变;
(2)如图2,连接EF,设EF交BD于点M,当t=2时,求AM的长;
(3)如图3,点G,H分别在边AB,CD上,且GH=3cm,连接EF,当EF与GH的夹角为45°,求t的值.
解:(1)等腰直角三角形.理由如下:
如图1,在正方形ABCD中,DC=BC,∠D=∠ABC=90°.
依题意得:DE=BF=t.
在△CDE与△CBF中,
,
∴△CDE≌△CBF(SAS),
∴CF=CE,∠DCE=∠BCF,
∴∠ECF=∠BCF+∠BCE=∠DCE+∠BCE=∠BCD=90°,
∴△CEF是等腰直角三角形.
故答案是:等腰直角三角形.
(2)如图2,过点E作EN∥AB,交BD于点N,则∠NEM=∠BFM.
∴∠END=∠ABD=∠EDN=45°,
∴EN=ED=BF.
在△EMN与△FMB中,
,
∴△EMN≌△FMB(AAS),
∴EM=FM.
∵Rt△AEF中,AE=4,AF=8,
∴=EF==4,
∴AM=EF=2;
(3)如图3,连接CE,CF,EF与GH交于P.
由(1)得∠CFE=45°,又∠EPQ=45°,
∴GH∥CF,
又∵AF∥DC,
∴四边形GFCH是平行四边形,
∴CF=GH=3,
在Rt△CBF中,得BF===3,
∴t=3.
同课章节目录
