甘肃省金昌市第一中学2011-2012学年高二下学期期中考试数学(理)试题
文档属性
| 名称 | 甘肃省金昌市第一中学2011-2012学年高二下学期期中考试数学(理)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 196.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-23 13:45:18 | ||
图片预览




文档简介
本试卷共8页,22小题,满分150分.考试用时120分钟.
题号 一 二 三 总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号、座位号等信息;
2.请将答案正确填写在答题卡上.
第I卷(选择题)
评卷人 得分
一、选择题(本大题共12小题,每小题5分,满分60分,在每小题给出的四个选项中,只有一项是符合题目要求的.)
1、复数的虚部是·····································( )
A.1 B.-1 C.0 D.
2、函数的导数为····························( )
A. B.
C. D.
3、定积分的值为·······························( )
A.0 B. C. D.-2
4、(x-)9的展开式的第8项······························( )
A. B. C. D.
5、火车上有10名乘客,沿途有5个车站,乘客下车的可能方式有( )
A.50种 B.种 C.种 D.520种
6、若,则的值为·············( )
A. B. C. D.
7、用反证法证明命题“,可被5整除,那么中至少有一个能被5整除”时,假设的内容应为······································( )
A.都能被5整除 B.都不能被5整除
C.至多有一个不能被5整除 D.至多有一个能被5整除
8、设随即变量服从正态分布,,则等于 ( )
A. B. C. D.
9、若,则等于·····································( )
A.5 B.6 C.7 D.8
10、在一次英语考试中,考试成绩服从正态分布,那么考试成绩在区间(88,112)内的概率是··········································( )
A.0.683 B.0.371 C.0.954 D.0.997
11、现用4种不同颜色要对如图所示的四个部分进行着色,要求有公共边界的两块不能用同一种颜色,则不同的着色方法共有···························( )
A.24种 B.30种 C.36种 D.48种
12、已知函数的导函数的图象如图,则···········( )
A.函数有2个极大值点,3个极小值点
B.函数有1个极大值点,1个极小值点
C.函数有3个极大值点,1个极小值点
D.函数有1个极大值点,3个极小值点
第II卷(非选择题)
评卷人 得分
二、填空题(本大题共4小题,每小题5分,共20分.)
13、已知则
14、一离散型随机变量的概率分布列如下,且则
0 1 2 3
0.1 0.1
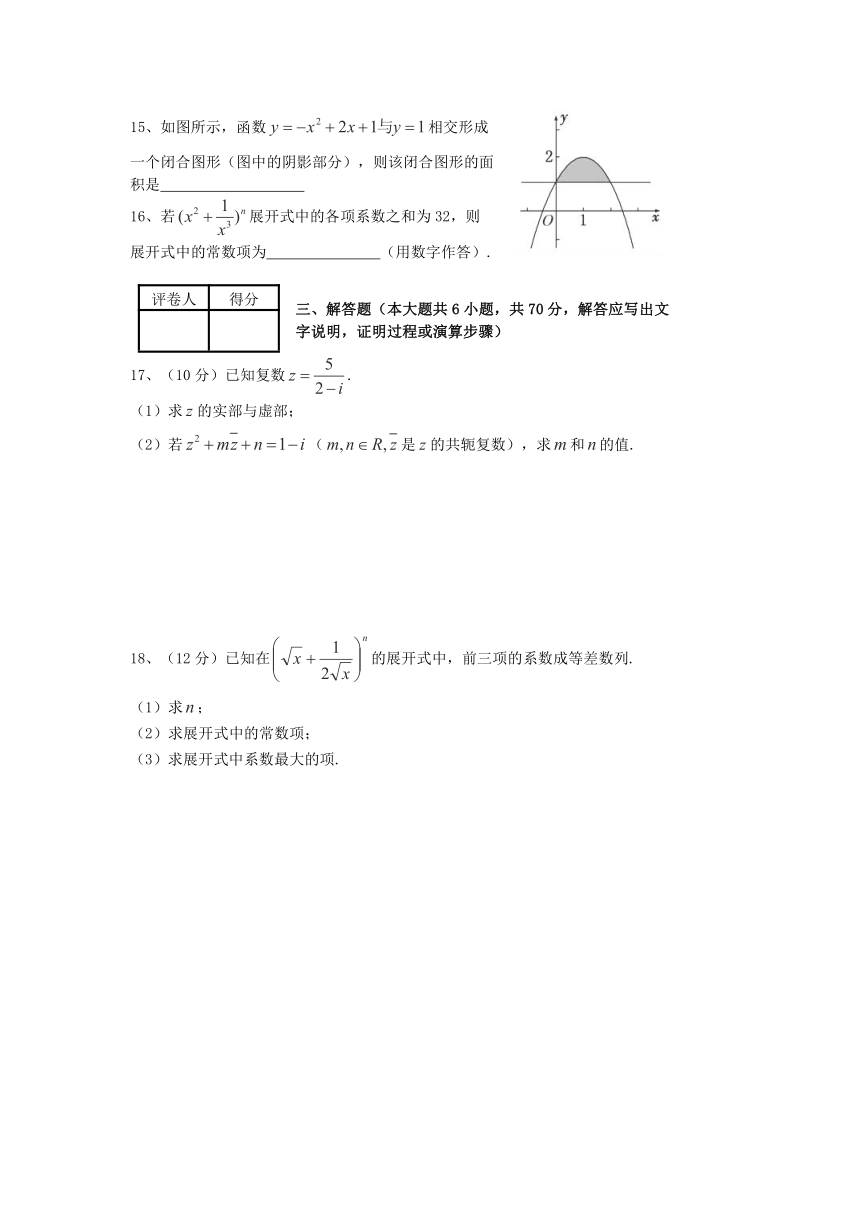
15、如图所示,函数相交形成
一个闭合图形(图中的阴影部分),则该闭合图形的面
积是
16、若展开式中的各项系数之和为32,则
展开式中的常数项为 (用数字作答).
评卷人 得分
三、解答题(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤)
17、(10分)已知复数.
(1)求的实部与虚部;
(2)若(是的共轭复数),求和的值.
18、(12分)已知在的展开式中,前三项的系数成等差数列.
(1)求;
(2)求展开式中的常数项;
(3)求展开式中系数最大的项.
19、(12分)7名师生站成一排照相留念,其中老师1人,男生4人,女生2人,在下列情况下,各有不同站法多少种?
(1)两名女生必须相邻而站;
(2)4名男生互不相邻;
(3)若4名男生身高都不等,按从高到低的顺序站;
(4)老师不站中间,女生不站两端.
20、(12分)函数,已知是奇函数.
(1)求的值;
(2)求的单调区间;
(3)求的极值.
21、(12分)已知箱子中有10个球,期中8个是正品,2个是次品,若每次取出1个球,取出后不放回,求:
(1)取两次就能取到2个正品的概率;
(2)取三次才能取到2个正品的概率;
(3)取四次才能取到2个正品的概率.
22、(12分)乒乓球单打比赛在甲、乙两名运动员间进行,比赛采用局胜制(即先胜局者获胜,比赛结束),假设两人在每一局比赛中获胜的可能性相同.
(1)求甲以比获胜的概率;
(2)求乙获胜且比赛局数多于局的概率;
(3)求比赛局数的分布列,并求.
高二数学理科答案
一、选择题答案:
1-5 BBDCC 6-10 CBDCC 11-12 DB
二、填空题:
13、103 14、0 15、 16、10
三、解答题:
17、 (1)实部:2 虚部:1 (2)
18、(1) (2)常数项:
(3)由题意,得:,∵r∈N,∴r=2或3
∴展开式中系数最大的项为.
19、(1) (2)
(3) (4)
20、(1)= ……2分
,可得:
=
……6分
(2), ……7分
如下图所示:
所以g(x)的增区间为和,减区间为
当时,g(x)取得极大值为;
当时,g(x)取得极小值为
21、 (1) (2)
(3)
22、(1)解:由已知,甲、乙两名运动员在每一局比赛中获胜的概率都是.
记“甲以比获胜”为事件,
则.
(2)解:记“乙获胜且比赛局数多于局”为事件.
因为,乙以比获胜的概率为,
乙以比获胜的概率为,
所以 .
(3)解:设比赛的局数为,则的可能取值为.
, ,
, .
比赛局数的分布列为:
题号 一 二 三 总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号、座位号等信息;
2.请将答案正确填写在答题卡上.
第I卷(选择题)
评卷人 得分
一、选择题(本大题共12小题,每小题5分,满分60分,在每小题给出的四个选项中,只有一项是符合题目要求的.)
1、复数的虚部是·····································( )
A.1 B.-1 C.0 D.
2、函数的导数为····························( )
A. B.
C. D.
3、定积分的值为·······························( )
A.0 B. C. D.-2
4、(x-)9的展开式的第8项······························( )
A. B. C. D.
5、火车上有10名乘客,沿途有5个车站,乘客下车的可能方式有( )
A.50种 B.种 C.种 D.520种
6、若,则的值为·············( )
A. B. C. D.
7、用反证法证明命题“,可被5整除,那么中至少有一个能被5整除”时,假设的内容应为······································( )
A.都能被5整除 B.都不能被5整除
C.至多有一个不能被5整除 D.至多有一个能被5整除
8、设随即变量服从正态分布,,则等于 ( )
A. B. C. D.
9、若,则等于·····································( )
A.5 B.6 C.7 D.8
10、在一次英语考试中,考试成绩服从正态分布,那么考试成绩在区间(88,112)内的概率是··········································( )
A.0.683 B.0.371 C.0.954 D.0.997
11、现用4种不同颜色要对如图所示的四个部分进行着色,要求有公共边界的两块不能用同一种颜色,则不同的着色方法共有···························( )
A.24种 B.30种 C.36种 D.48种
12、已知函数的导函数的图象如图,则···········( )
A.函数有2个极大值点,3个极小值点
B.函数有1个极大值点,1个极小值点
C.函数有3个极大值点,1个极小值点
D.函数有1个极大值点,3个极小值点
第II卷(非选择题)
评卷人 得分
二、填空题(本大题共4小题,每小题5分,共20分.)
13、已知则
14、一离散型随机变量的概率分布列如下,且则
0 1 2 3
0.1 0.1
15、如图所示,函数相交形成
一个闭合图形(图中的阴影部分),则该闭合图形的面
积是
16、若展开式中的各项系数之和为32,则
展开式中的常数项为 (用数字作答).
评卷人 得分
三、解答题(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤)
17、(10分)已知复数.
(1)求的实部与虚部;
(2)若(是的共轭复数),求和的值.
18、(12分)已知在的展开式中,前三项的系数成等差数列.
(1)求;
(2)求展开式中的常数项;
(3)求展开式中系数最大的项.
19、(12分)7名师生站成一排照相留念,其中老师1人,男生4人,女生2人,在下列情况下,各有不同站法多少种?
(1)两名女生必须相邻而站;
(2)4名男生互不相邻;
(3)若4名男生身高都不等,按从高到低的顺序站;
(4)老师不站中间,女生不站两端.
20、(12分)函数,已知是奇函数.
(1)求的值;
(2)求的单调区间;
(3)求的极值.
21、(12分)已知箱子中有10个球,期中8个是正品,2个是次品,若每次取出1个球,取出后不放回,求:
(1)取两次就能取到2个正品的概率;
(2)取三次才能取到2个正品的概率;
(3)取四次才能取到2个正品的概率.
22、(12分)乒乓球单打比赛在甲、乙两名运动员间进行,比赛采用局胜制(即先胜局者获胜,比赛结束),假设两人在每一局比赛中获胜的可能性相同.
(1)求甲以比获胜的概率;
(2)求乙获胜且比赛局数多于局的概率;
(3)求比赛局数的分布列,并求.
高二数学理科答案
一、选择题答案:
1-5 BBDCC 6-10 CBDCC 11-12 DB
二、填空题:
13、103 14、0 15、 16、10
三、解答题:
17、 (1)实部:2 虚部:1 (2)
18、(1) (2)常数项:
(3)由题意,得:,∵r∈N,∴r=2或3
∴展开式中系数最大的项为.
19、(1) (2)
(3) (4)
20、(1)= ……2分
,可得:
=
……6分
(2), ……7分
如下图所示:
所以g(x)的增区间为和,减区间为
当时,g(x)取得极大值为;
当时,g(x)取得极小值为
21、 (1) (2)
(3)
22、(1)解:由已知,甲、乙两名运动员在每一局比赛中获胜的概率都是.
记“甲以比获胜”为事件,
则.
(2)解:记“乙获胜且比赛局数多于局”为事件.
因为,乙以比获胜的概率为,
乙以比获胜的概率为,
所以 .
(3)解:设比赛的局数为,则的可能取值为.
, ,
, .
比赛局数的分布列为:
同课章节目录
