《第1章全等三角形》单元综合能力提升训练202-2022学年苏科版八年级数学上册(word版含解析)
文档属性
| 名称 | 《第1章全等三角形》单元综合能力提升训练202-2022学年苏科版八年级数学上册(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-29 09:28:52 | ||
图片预览


文档简介
2021年苏科版八年级数学上册《第1章全等三角形》单元综合能力提升训练(附答案)
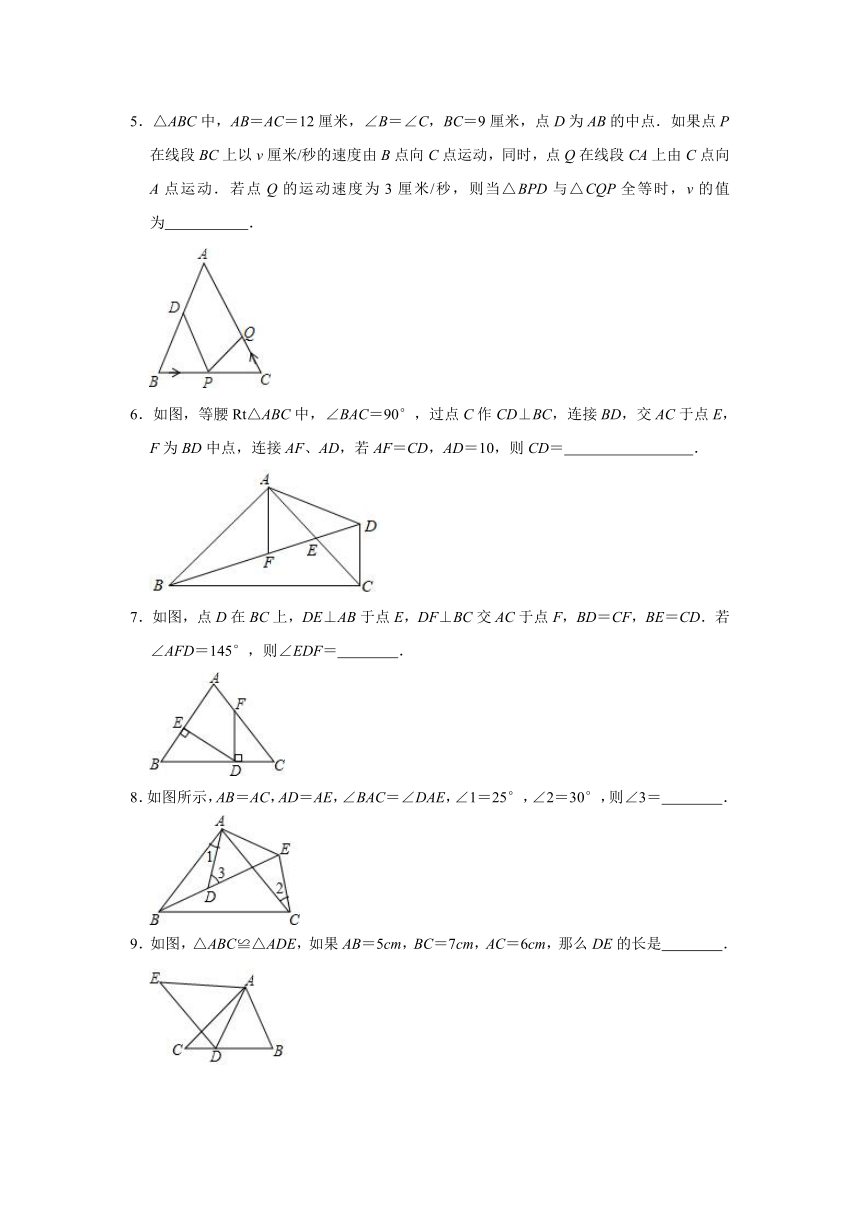
1.如图,△ABC≌△DEC,点A和点D是对应顶点,点B和点E是对应顶点,过点A作AF⊥CD,垂足为点F,若∠BCE=65°,则∠CAF的度数为( )
A.30°
B.25°
C.35°
D.65°
2.如图,AB⊥CD,且AB=CD,E,F是AD上两点,CE⊥AD,BF⊥AD.若CE=4,BF=3,EF=2,则AD的长为( )
A.3
B.5
C.6
D.7
3.如图,△ABC中,点D、点E分别在边AB、BC上,连结AE、DE,若△ADE≌△BDE,AC:AB:BC=2:3:4,且△ABC的周长比△AEC的周长大6.则△AEC的周长为
.
4.如图所示,△BKC≌△BKE≌△DKC,BE与KD交于点G,KE与CD交于点P,BE与CD交于点A,∠BKC=134°,∠E=22°,则∠KPD=
.
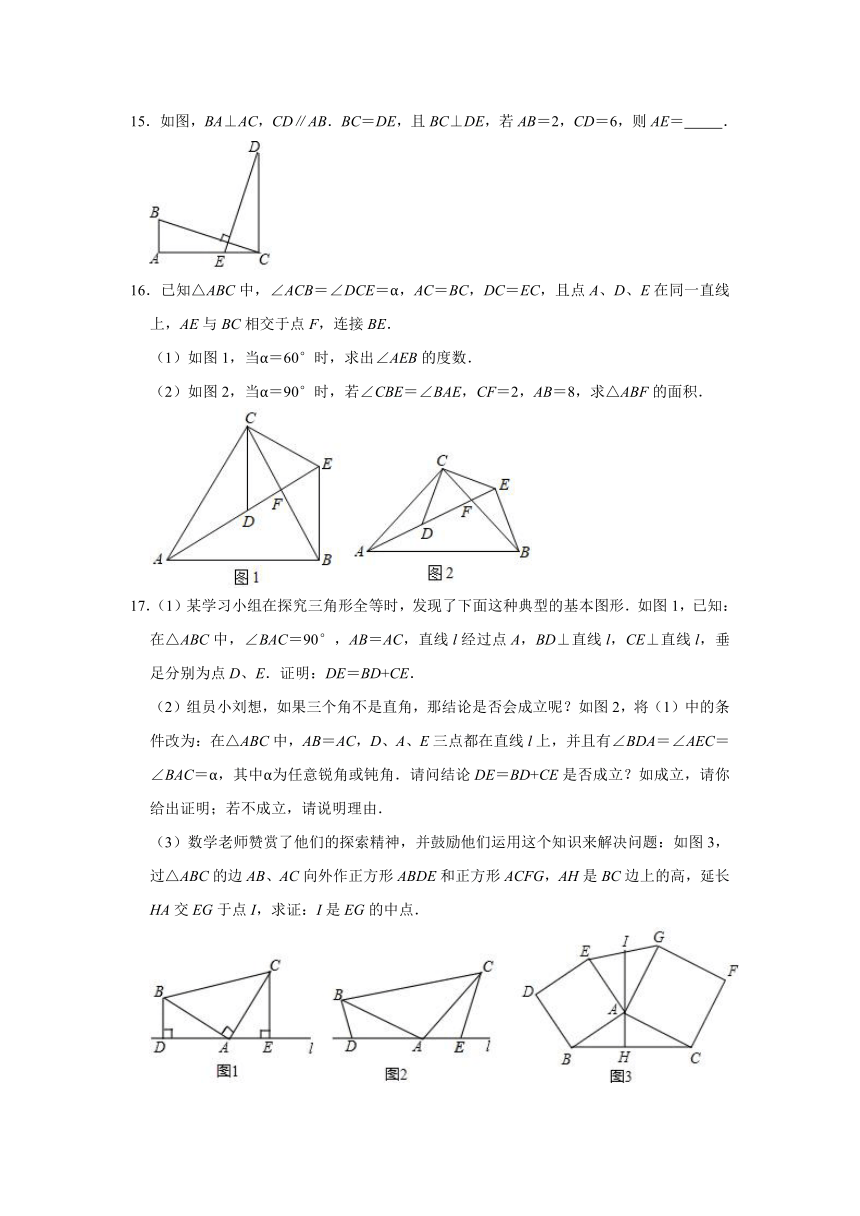
5.△ABC中,AB=AC=12厘米,∠B=∠C,BC=9厘米,点D为AB的中点.如果点P在线段BC上以v厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为3厘米/秒,则当△BPD与△CQP全等时,v的值为
.
6.如图,等腰Rt△ABC中,∠BAC=90°,过点C作CD⊥BC,连接BD,交AC于点E,F为BD中点,连接AF、AD,若AF=CD,AD=10,则CD=
.
7.如图,点D在BC上,DE⊥AB于点E,DF⊥BC交AC于点F,BD=CF,BE=CD.若∠AFD=145°,则∠EDF=
.
8.如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=
.
9.如图,△ABC≌△ADE,如果AB=5cm,BC=7cm,AC=6cm,那么DE的长是
.
10.如图所示的网格是正方形网格,图形的各个顶点均为格点,则∠1+∠2=
.
11.如图,△ABC中,∠C=60°,取BC上一点D,连接AD,使AD=BD,延长CA至E,连接ED,且∠DAE=2∠AED,若BC=4AE,AC=3,则BC的长度为
.
12.如图,在△ABC中,∠ABC=45°,AC=9cm,F是高AD和BE的交点,则BF的长是
.
13.如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为
.
14.如图,在△ABC中,∠A=90°,AB=AC,∠ABC的平分线BD交AC于点D,CE⊥BD,交BD的延长线于点E,若BD=8,则CE=
.
15.如图,BA⊥AC,CD∥AB.BC=DE,且BC⊥DE,若AB=2,CD=6,则AE=
.
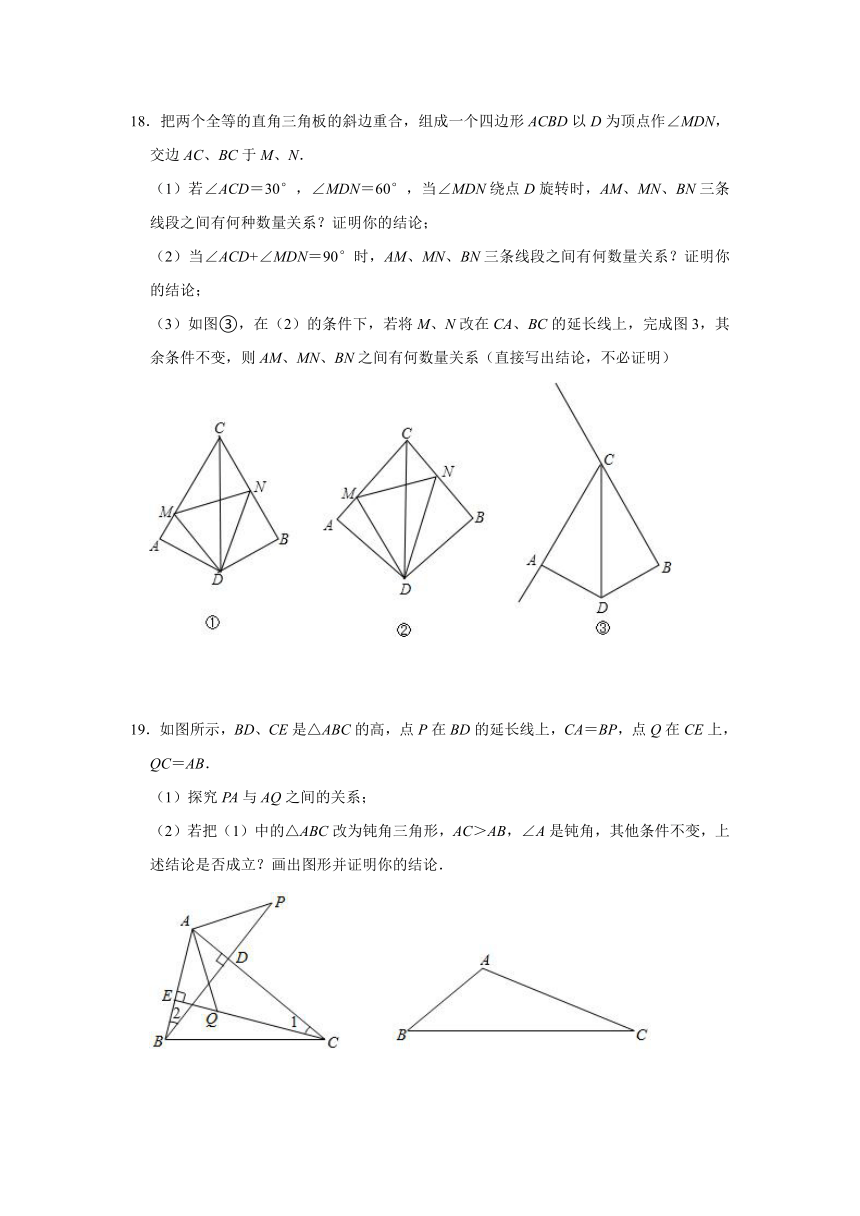
16.已知△ABC中,∠ACB=∠DCE=α,AC=BC,DC=EC,且点A、D、E在同一直线上,AE与BC相交于点F,连接BE.
(1)如图1,当α=60°时,求出∠AEB的度数.
(2)如图2,当α=90°时,若∠CBE=∠BAE,CF=2,AB=8,求△ABF的面积.
17.(1)某学习小组在探究三角形全等时,发现了下面这种典型的基本图形.如图1,已知:在△ABC中,∠BAC=90°,AB=AC,直线l经过点A,BD⊥直线l,CE⊥直线l,垂足分别为点D、E.证明:DE=BD+CE.
(2)组员小刘想,如果三个角不是直角,那结论是否会成立呢?如图2,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线l上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:如图3,过△ABC的边AB、AC向外作正方形ABDE和正方形ACFG,AH是BC边上的高,延长HA交EG于点I,求证:I是EG的中点.
18.把两个全等的直角三角板的斜边重合,组成一个四边形ACBD以D为顶点作∠MDN,交边AC、BC于M、N.
(1)若∠ACD=30°,∠MDN=60°,当∠MDN绕点D旋转时,AM、MN、BN三条线段之间有何种数量关系?证明你的结论;
(2)当∠ACD+∠MDN=90°时,AM、MN、BN三条线段之间有何数量关系?证明你的结论;
(3)如图③,在(2)的条件下,若将M、N改在CA、BC的延长线上,完成图3,其余条件不变,则AM、MN、BN之间有何数量关系(直接写出结论,不必证明)
19.如图所示,BD、CE是△ABC的高,点P在BD的延长线上,CA=BP,点Q在CE上,QC=AB.
(1)探究PA与AQ之间的关系;
(2)若把(1)中的△ABC改为钝角三角形,AC>AB,∠A是钝角,其他条件不变,上述结论是否成立?画出图形并证明你的结论.
20.如图1,在△ABC中,AE⊥BC于点E,AE=BE,D是AE上的一点,且DE=CE,连接BD,CD.
(1)试判断BD与AC的位置关系和数量关系,并说明理由;
(2)如图2,若将△DCE绕点E旋转一定的角度后,试判断BD与AC的位置关系和数量关系是否发生变化,并说明理由.
21.已知△ABC和△ADE均为等腰三角形,且∠BAC=∠DAE,AB=AC,AD=AE.
(1)如图1,点E在BC上,求证:BC=BD+BE;
(2)如图2,点E在CB的延长线上,(1)的结论是否成立?若成立,给出证明;若不成立,写出成立的式子并证明.
参考答案
1.解:∵△ABC≌△DEC,
∴∠ACB=∠DCE,
∵∠BCE=65°,
∴∠ACD=∠BCE=65°,
∵AF⊥CD,
∴∠AFC=90°,
∴∠CAF+∠ACD=90°,
∴∠CAF=90°﹣65°=25°,
故选:B.
2.解:∵AB⊥CD,CE⊥AD,BF⊥AD,
∴∠AFB=∠CED=90°,∠A+∠D=90°,∠C+∠D=90°,
∴∠A=∠C,∵AB=CD,
∴△ABF≌△CDE(AAS),
∴AF=CE=4,BF=DE=3,
∵EF=2,
∴AD=AF+DF=4+(3﹣2)=5,
故选:B.
3.解:∵△ADE≌△BDE,
∴BE=AE.
∴C△AEC=AE+EC+AC=BE+EC+AC=BC+AC.
∵AC:AB:BC=2:3:4,
∴设AC=2x,AB=3x,BC=4x.
∵△ABC的周长比△AEC的周长大6,
∴C△ABC﹣C△AEC=6.
∴(AB+BC+AC)﹣(BC+AC)=6.
∴AB=3x=6.
∴x=2.
∴AC=2x=4,BC=4x=8.
∴C△AEC=BC+AC=8+4=12.
故答案为:12.
4.解:∵△BKC≌△BKE,∠BKC=134°,
∴∠BKE=∠BKC=134°,
∴∠PKC=360°﹣134°﹣134°=92°,
∵△BKE≌△DKC,∠E=22°,
∴∠DCK=∠E=22°,
∴∠KPD=∠PKC+∠DCK=92°+22°=114°,
故答案为:114°.
5.解:∵△ABC中,AB=AC=12厘米,点D为AB的中点,
∴BD=6厘米,
若△BPD≌△CPQ,则需BD=CQ=6厘米,BP=CP=BC=×9=4.5(厘米),
∵点Q的运动速度为3厘米/秒,
∴点Q的运动时间为:6÷3=2(s),
∴v=4.5÷2=2.25(厘米/秒);
若△BPD≌△CQP,则需CP=BD=6厘米,BP=CQ,
∴,
解得:v=3;
∴v的值为:2.25或3,
故答案为:2.25或3
6.解:
延长AF交BC于点M,连接FC,
∵DC⊥BC,点F为BD的中点,
∴FC=BD=FB,
∴点F在线段BC的垂直平分线上,
∵△ABC是等腰直角三角形,
∴AB=AC,即点A是线段BC垂直平分线上的点,
∴AM是线段BC的垂直平分线,
∴AM⊥BC,BM=CM=AM,
∵DC⊥BC,AM⊥BC,
∴AM||DC,
∴FM=DC,
∵AF=DC,AM=AF+FM,
∴FM=AM=MC,
∵AM||DC,AF=DC,
∴四边形AFCD是平行四边形,
又∵AD=10,
∴FC=AD=10,
设FM=x,MC=3x,
在Rt△FMC中,∵FM2+MC2=FC2,
∴x2+(3x)2=102,解得x=,
∴FM=,
∴CD=2FM=.
故答案是,
7.解:如图,∵∠DFC+∠AFD=180°,∠AFD=145°,
∴∠CFD=35°.
又∵DE⊥AB,DF⊥BC,
∴∠BED=∠CDF=90°,
在Rt△BDE与△Rt△CFD中,
,
∴Rt△BDE≌△Rt△CFD(HL),
∴∠BDE=∠CFD=35°,
∴∠EDF+∠BDE=∠EDF+∠CFD=90°,
∴∠EDF=55°.
故答案是:55°.
8.解:∵∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠1=∠EAC,
在△BAD和△CAE中,
∴△BAD≌△CAE(SAS),
∴∠2=∠ABD=30°,
∵∠1=25°,
∴∠3=∠1+∠ABD=25°+30°=55°,
故答案为:55°.
9.解:∵△ABC≌△ADE,BC=7,
∴DE=BC=7(cm),
故答案为:7cm.
10.解:如图所示:
由题意可得:∠1=∠3,
则∠1+∠2=∠2+∠3=45°.
故答案为:45°.
11.解:延长CE至H,使CH=CB,连接BH,作DG∥CH交BH于G,延长AC至F,使AF=AD,连接DF、EG,如图所示:
则∠ADF=∠AFD,∠EDG=∠AED,∠DGB=∠H,
设∠AED=x,
∵∠DAE=2∠AED=2x,
∴∠ADF=∠AFD=∠DAE=x=∠AED=∠DEG,
∴DE=DF,
∵∠ACB=60°,AH=CB,
∴△BCH是等边三角形,
∴CB=BH,∠CBH=∠H=60°,
∴∠DGB=∠CBH=60°,
∴△BDG是等边三角形,
∴BD=GD=BG=AD=AF,
∴GH=BG,
在△ADF和△GED中,,
∴△ADF≌△GED(SAS),
∴AF=AD=GE=DG,∠ADF=∠GED=x,
∴∠AEG=2x=∠EAD,
∴∠GEH=∠DAC,
在△HEG和△CAD中,,
∴△HEG≌△CAD(AAS),
∴EH=AC=3,
∵BC=CH=3+AE+3,BC=4AE,
∴6+AE=4AE,
解得:AE=2,
∴BC=8;
故答案为:8.
12.解:∵AD⊥BC,BE⊥AC,
∴∠ADC=∠ADB=90°,∠BEA=90°,
又∵∠FBD+∠BDF+∠BFD=180°,∠FAE+∠FEA+∠AFE=180°,且∠BFD=∠AFE,
∴∠FBD=∠FAE,
又∵∠ABC=45°,∠ABD+∠BAD=90°,
∴∠BAD=45°,
∴BD=AD,且∠ADC=∠BDF=90°,∠FBD=∠FAE,
∴△ADC≌△BDF(ASA)
∴BF=AC=9cm,
故答案为:9cm.
13.解:由平移的性质知,BE=6,DE=AB=10,
∴OE=DE﹣DO=10﹣4=6,
∴S四边形ODFC=S梯形ABEO=(AB+OE)?BE=(10+6)×6=48.
故答案为48.
14.解:如图,延长BA、CE相交于点F,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
在△BCE和△BFE中,
,
∴△BCE≌△BFE(ASA),
∴CE=EF,
∵∠BAC=90°,CE⊥BD,
∴∠ACF+∠F=90°,∠ABD+∠F=90°,
∴∠ABD=∠ACF,
在△ABD和△ACF中,
,
∴△ABD≌△ACF(ASA),
∴BD=CF,
∵CF=CE+EF=2CE,
∴BD=2CE=8,
∴CE=4.
故答案为:4.
15.解:∵BA⊥AC,
∴∠A=90°,
∵CD∥AB,
∴∠DCE=90°,
∵BC⊥DE,
∴∠DCB+∠D=90°,
∵∠DCB+∠BCA=90°,
∴∠BCA=∠D,
在△ABC和△CED中
,
∴△ABC≌△CED(AAS),
∴AB=CE=2,AC=CD=6,
∴AE=AC﹣CE=6﹣2=4.
故答案为4.
16.解:(1)∵∠ACB=∠DCE=60°,CA=CB,CD=CE,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS),
∴∠CAD=∠CBE,
∵∠CFA=∠BFE,
∴∠AEB=∠ACF=60°.
(2)同理可证△ACD≌△BCE,
∴∠CAF=∠CBE,
∵∠CBE=∠BAE,
∴∠CAF=∠BAE,
∴AF平分∠CAB,
∵FC⊥AC,CF=2,
∴点F到AB的距离=CF=2,
∴S△ABF=?AB?CF=×8×2=8.
17.解:(1)如图1,
∵BD⊥直线l,CE⊥直线l,
∴∠BDA=∠CEA=90°,
∵∠BAC=90°,
∴∠BAD+∠CAE=90°
∵∠BAD+∠ABD=90°,
∴∠CAE=∠ABD
在△ADB和△CEA中,
,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE;
(2)DE=BD+CE.
如图2,
证明如下:
∵∠BDA=∠BAC=α,
∴∠DBA+∠BAD=∠BAD+∠CAE=180°﹣α,
∴∠DBA=∠CAE,
在△ADB和△CEA中.
.
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE
(3)如图3,
过E作EM⊥HI于M,GN⊥HI的延长线于N.
∴∠EMI=GNI=90°
由(1)和(2)的结论可知EM=AH=GN
∴EM=GN
在△EMI和△GNI中,
,
∴△EMI≌△GNI(AAS),
∴EI=GI,
∴I是EG的中点.
18.
(1)AM+BN=MN,
证明:延长CB到E,使BE=AM,
∵∠A=∠CBD=90°,
∴∠A=∠EBD=90°,
在△DAM和△DBE中
,
∴△DAM≌△DBE,
∴∠BDE=∠MDA,DM=DE,
∵∠MDN=∠ADC=60°,
∴∠ADM=∠NDC,
∴∠BDE=∠NDC,
∴∠MDN=∠NDE,
在△MDN和△EDN中
,
∴△MDN≌△EDN,
∴MN=NE,
∵NE=BE+BN=AM+BN,
∴AM+BN=MN.
(2)AM+BN=MN,
证明:延长CB到E,使BE=AM,连接DE,
∵∠A=∠CBD=90°,
∴∠A=∠DBE=90°,
∵∠CDA+∠ACD=90°,∠MDN+∠ACD=90°,
∴∠MDN=∠CDA,
∵∠MDN=∠BDC,
∴∠MDA=∠CDN,∠CDM=∠NDB,
在△DAM和△DBE中
,
∴△DAM≌△DBE,
∴∠BDE=∠MDA=∠CDN,DM=DE,
∵∠MDN+∠ACD=90°,∠ACD+∠ADC=90°,
∴∠NDM=∠ADC=∠CDB,
∴∠ADM=∠CDN=∠BDE,
∵∠CDM=∠NDB
∴∠MDN=∠NDE,
在△MDN和△EDN中
,
∴△MDN≌△EDN,
∴MN=NE,
∵NE=BE+BN=AM+BN,
∴AM+BN=MN.
(3)BN﹣AM=MN,
证明:在CB截取BE=AM,连接DE,
∵∠CDA+∠ACD=90°,∠MDN+∠ACD=90°,
∴∠MDN=∠CDA,
∵∠ADN=∠ADN,
∴∠MDA=∠CDN,
∵∠B=∠CAD=90°,
∴∠B=∠DAM=90°,
在△DAM和△DBE中
,
∴△DAM≌△DBE,
∴∠BDE=∠ADM=∠CDN,DM=DE,
∵∠ADC=∠BDC=∠MDN,
∴∠MDN=∠EDN,
在△MDN和△EDN中
,
∴△MDN≌△EDN,
∴MN=NE,
∵NE=BN﹣BE=BN﹣AM,
∴BN﹣AM=MN.
19.(1)结论:AP=AQ,AP⊥AQ
证明:∵BD、CE是△ABC的高,
∴BD⊥AC,CE⊥AB,
∴∠1+∠CAB=90°,∠2+∠CAB=90°,
∴∠1=∠2,
在△QAC和△APB中,
,
∴△QAC≌△APB(SAS),
∴AQ=AP,∠QAC=∠P,
而∠DAP+∠P=90°,
∴∠DAP+∠QAC=90°,
即∠QAP=90°,
∴AQ⊥AP;
即AP=AQ,AP⊥AQ;
(2)上述结论成立,理由如下:
如图所示:
∵BD、CE是△ABC的高,
∴BD⊥AC,CE⊥AB,
∴∠1+∠CAE=90°,∠2+∠DAB=90°,
∵∠CAE=∠DAB,
∴∠1=∠2,
在△QAC和△APB中,
,
∴△QAC≌△APB(SAS),
∴AQ=AP,∠QAC=∠P,
∵∠PDA=90°,
∴∠P+∠PAD=90°,
∴∠QAC+∠PAD=90°,
∴∠QAP=90°,
∴AQ⊥AP,
即AP=AQ,AP⊥AQ.
20.解:(1)BD=AC,BD⊥AC,
理由:延长BD交AC于F.
∵AE⊥BC,
∴∠AEB=∠AEC=90°,
在△BED和△AEC中,
,
∴△BED≌△AEC(SAS),
∴BD=AC,∠DBE=∠CAE,
∵∠BED=90°,
∴∠EBD+∠BDE=90°,
∵∠BDE=∠ADF,
∴∠ADF+∠CAE=90°,
∴∠AFD=180°﹣90°=90°,
∴BD⊥AC;
(2)结论不发生变化,
理由是:设AC与DE相交于点O,
∵∠BEA=∠DEC=90°,
∴∠BEA+∠AED=∠DEC+∠AED,
∴∠BED=∠AEC,
在△BED和△AEC中,
,
∴△BED≌△AEC(SAS),
∴BD=AC,∠BDE=∠ACE,
∵∠DEC=90°,
∴∠ACE+∠EOC=90°,
∵∠EOC=∠DOF,
∴∠BDE+∠DOF=90°,
∴∠DFO=180°﹣90°=90°,
∴BD⊥AC.
21.(1)证明:∵∠BAC=∠DAE,
∴∠BAC﹣∠BAE=∠DAE﹣∠BAE,
即∠DAB=∠EAC,
又∵AB=AC,AD=AE,
∴△DAB≌△EAC(SAS),
∴BD=CE,
∴BC=BE+CE=BD+BE;
(2)解:(1)的结论不成立,成立的结论是BC=BD﹣BE.
证明:∵∠BAC=∠DAE,
∴∠BAC+∠EAB=∠DAE+∠EAB,
即∠DAB=∠EAC,
又∵AB=AC,AD=AE,
∴△DAB≌△EAC(SAS),
∴BD=CE,
∴BC=CE﹣BE=BD﹣BE.
1.如图,△ABC≌△DEC,点A和点D是对应顶点,点B和点E是对应顶点,过点A作AF⊥CD,垂足为点F,若∠BCE=65°,则∠CAF的度数为( )
A.30°
B.25°
C.35°
D.65°
2.如图,AB⊥CD,且AB=CD,E,F是AD上两点,CE⊥AD,BF⊥AD.若CE=4,BF=3,EF=2,则AD的长为( )
A.3
B.5
C.6
D.7
3.如图,△ABC中,点D、点E分别在边AB、BC上,连结AE、DE,若△ADE≌△BDE,AC:AB:BC=2:3:4,且△ABC的周长比△AEC的周长大6.则△AEC的周长为
.
4.如图所示,△BKC≌△BKE≌△DKC,BE与KD交于点G,KE与CD交于点P,BE与CD交于点A,∠BKC=134°,∠E=22°,则∠KPD=
.
5.△ABC中,AB=AC=12厘米,∠B=∠C,BC=9厘米,点D为AB的中点.如果点P在线段BC上以v厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为3厘米/秒,则当△BPD与△CQP全等时,v的值为
.
6.如图,等腰Rt△ABC中,∠BAC=90°,过点C作CD⊥BC,连接BD,交AC于点E,F为BD中点,连接AF、AD,若AF=CD,AD=10,则CD=
.
7.如图,点D在BC上,DE⊥AB于点E,DF⊥BC交AC于点F,BD=CF,BE=CD.若∠AFD=145°,则∠EDF=
.
8.如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=
.
9.如图,△ABC≌△ADE,如果AB=5cm,BC=7cm,AC=6cm,那么DE的长是
.
10.如图所示的网格是正方形网格,图形的各个顶点均为格点,则∠1+∠2=
.
11.如图,△ABC中,∠C=60°,取BC上一点D,连接AD,使AD=BD,延长CA至E,连接ED,且∠DAE=2∠AED,若BC=4AE,AC=3,则BC的长度为
.
12.如图,在△ABC中,∠ABC=45°,AC=9cm,F是高AD和BE的交点,则BF的长是
.
13.如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为
.
14.如图,在△ABC中,∠A=90°,AB=AC,∠ABC的平分线BD交AC于点D,CE⊥BD,交BD的延长线于点E,若BD=8,则CE=
.
15.如图,BA⊥AC,CD∥AB.BC=DE,且BC⊥DE,若AB=2,CD=6,则AE=
.
16.已知△ABC中,∠ACB=∠DCE=α,AC=BC,DC=EC,且点A、D、E在同一直线上,AE与BC相交于点F,连接BE.
(1)如图1,当α=60°时,求出∠AEB的度数.
(2)如图2,当α=90°时,若∠CBE=∠BAE,CF=2,AB=8,求△ABF的面积.
17.(1)某学习小组在探究三角形全等时,发现了下面这种典型的基本图形.如图1,已知:在△ABC中,∠BAC=90°,AB=AC,直线l经过点A,BD⊥直线l,CE⊥直线l,垂足分别为点D、E.证明:DE=BD+CE.
(2)组员小刘想,如果三个角不是直角,那结论是否会成立呢?如图2,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线l上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:如图3,过△ABC的边AB、AC向外作正方形ABDE和正方形ACFG,AH是BC边上的高,延长HA交EG于点I,求证:I是EG的中点.
18.把两个全等的直角三角板的斜边重合,组成一个四边形ACBD以D为顶点作∠MDN,交边AC、BC于M、N.
(1)若∠ACD=30°,∠MDN=60°,当∠MDN绕点D旋转时,AM、MN、BN三条线段之间有何种数量关系?证明你的结论;
(2)当∠ACD+∠MDN=90°时,AM、MN、BN三条线段之间有何数量关系?证明你的结论;
(3)如图③,在(2)的条件下,若将M、N改在CA、BC的延长线上,完成图3,其余条件不变,则AM、MN、BN之间有何数量关系(直接写出结论,不必证明)
19.如图所示,BD、CE是△ABC的高,点P在BD的延长线上,CA=BP,点Q在CE上,QC=AB.
(1)探究PA与AQ之间的关系;
(2)若把(1)中的△ABC改为钝角三角形,AC>AB,∠A是钝角,其他条件不变,上述结论是否成立?画出图形并证明你的结论.
20.如图1,在△ABC中,AE⊥BC于点E,AE=BE,D是AE上的一点,且DE=CE,连接BD,CD.
(1)试判断BD与AC的位置关系和数量关系,并说明理由;
(2)如图2,若将△DCE绕点E旋转一定的角度后,试判断BD与AC的位置关系和数量关系是否发生变化,并说明理由.
21.已知△ABC和△ADE均为等腰三角形,且∠BAC=∠DAE,AB=AC,AD=AE.
(1)如图1,点E在BC上,求证:BC=BD+BE;
(2)如图2,点E在CB的延长线上,(1)的结论是否成立?若成立,给出证明;若不成立,写出成立的式子并证明.
参考答案
1.解:∵△ABC≌△DEC,
∴∠ACB=∠DCE,
∵∠BCE=65°,
∴∠ACD=∠BCE=65°,
∵AF⊥CD,
∴∠AFC=90°,
∴∠CAF+∠ACD=90°,
∴∠CAF=90°﹣65°=25°,
故选:B.
2.解:∵AB⊥CD,CE⊥AD,BF⊥AD,
∴∠AFB=∠CED=90°,∠A+∠D=90°,∠C+∠D=90°,
∴∠A=∠C,∵AB=CD,
∴△ABF≌△CDE(AAS),
∴AF=CE=4,BF=DE=3,
∵EF=2,
∴AD=AF+DF=4+(3﹣2)=5,
故选:B.
3.解:∵△ADE≌△BDE,
∴BE=AE.
∴C△AEC=AE+EC+AC=BE+EC+AC=BC+AC.
∵AC:AB:BC=2:3:4,
∴设AC=2x,AB=3x,BC=4x.
∵△ABC的周长比△AEC的周长大6,
∴C△ABC﹣C△AEC=6.
∴(AB+BC+AC)﹣(BC+AC)=6.
∴AB=3x=6.
∴x=2.
∴AC=2x=4,BC=4x=8.
∴C△AEC=BC+AC=8+4=12.
故答案为:12.
4.解:∵△BKC≌△BKE,∠BKC=134°,
∴∠BKE=∠BKC=134°,
∴∠PKC=360°﹣134°﹣134°=92°,
∵△BKE≌△DKC,∠E=22°,
∴∠DCK=∠E=22°,
∴∠KPD=∠PKC+∠DCK=92°+22°=114°,
故答案为:114°.
5.解:∵△ABC中,AB=AC=12厘米,点D为AB的中点,
∴BD=6厘米,
若△BPD≌△CPQ,则需BD=CQ=6厘米,BP=CP=BC=×9=4.5(厘米),
∵点Q的运动速度为3厘米/秒,
∴点Q的运动时间为:6÷3=2(s),
∴v=4.5÷2=2.25(厘米/秒);
若△BPD≌△CQP,则需CP=BD=6厘米,BP=CQ,
∴,
解得:v=3;
∴v的值为:2.25或3,
故答案为:2.25或3
6.解:
延长AF交BC于点M,连接FC,
∵DC⊥BC,点F为BD的中点,
∴FC=BD=FB,
∴点F在线段BC的垂直平分线上,
∵△ABC是等腰直角三角形,
∴AB=AC,即点A是线段BC垂直平分线上的点,
∴AM是线段BC的垂直平分线,
∴AM⊥BC,BM=CM=AM,
∵DC⊥BC,AM⊥BC,
∴AM||DC,
∴FM=DC,
∵AF=DC,AM=AF+FM,
∴FM=AM=MC,
∵AM||DC,AF=DC,
∴四边形AFCD是平行四边形,
又∵AD=10,
∴FC=AD=10,
设FM=x,MC=3x,
在Rt△FMC中,∵FM2+MC2=FC2,
∴x2+(3x)2=102,解得x=,
∴FM=,
∴CD=2FM=.
故答案是,
7.解:如图,∵∠DFC+∠AFD=180°,∠AFD=145°,
∴∠CFD=35°.
又∵DE⊥AB,DF⊥BC,
∴∠BED=∠CDF=90°,
在Rt△BDE与△Rt△CFD中,
,
∴Rt△BDE≌△Rt△CFD(HL),
∴∠BDE=∠CFD=35°,
∴∠EDF+∠BDE=∠EDF+∠CFD=90°,
∴∠EDF=55°.
故答案是:55°.
8.解:∵∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠1=∠EAC,
在△BAD和△CAE中,
∴△BAD≌△CAE(SAS),
∴∠2=∠ABD=30°,
∵∠1=25°,
∴∠3=∠1+∠ABD=25°+30°=55°,
故答案为:55°.
9.解:∵△ABC≌△ADE,BC=7,
∴DE=BC=7(cm),
故答案为:7cm.
10.解:如图所示:
由题意可得:∠1=∠3,
则∠1+∠2=∠2+∠3=45°.
故答案为:45°.
11.解:延长CE至H,使CH=CB,连接BH,作DG∥CH交BH于G,延长AC至F,使AF=AD,连接DF、EG,如图所示:
则∠ADF=∠AFD,∠EDG=∠AED,∠DGB=∠H,
设∠AED=x,
∵∠DAE=2∠AED=2x,
∴∠ADF=∠AFD=∠DAE=x=∠AED=∠DEG,
∴DE=DF,
∵∠ACB=60°,AH=CB,
∴△BCH是等边三角形,
∴CB=BH,∠CBH=∠H=60°,
∴∠DGB=∠CBH=60°,
∴△BDG是等边三角形,
∴BD=GD=BG=AD=AF,
∴GH=BG,
在△ADF和△GED中,,
∴△ADF≌△GED(SAS),
∴AF=AD=GE=DG,∠ADF=∠GED=x,
∴∠AEG=2x=∠EAD,
∴∠GEH=∠DAC,
在△HEG和△CAD中,,
∴△HEG≌△CAD(AAS),
∴EH=AC=3,
∵BC=CH=3+AE+3,BC=4AE,
∴6+AE=4AE,
解得:AE=2,
∴BC=8;
故答案为:8.
12.解:∵AD⊥BC,BE⊥AC,
∴∠ADC=∠ADB=90°,∠BEA=90°,
又∵∠FBD+∠BDF+∠BFD=180°,∠FAE+∠FEA+∠AFE=180°,且∠BFD=∠AFE,
∴∠FBD=∠FAE,
又∵∠ABC=45°,∠ABD+∠BAD=90°,
∴∠BAD=45°,
∴BD=AD,且∠ADC=∠BDF=90°,∠FBD=∠FAE,
∴△ADC≌△BDF(ASA)
∴BF=AC=9cm,
故答案为:9cm.
13.解:由平移的性质知,BE=6,DE=AB=10,
∴OE=DE﹣DO=10﹣4=6,
∴S四边形ODFC=S梯形ABEO=(AB+OE)?BE=(10+6)×6=48.
故答案为48.
14.解:如图,延长BA、CE相交于点F,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
在△BCE和△BFE中,
,
∴△BCE≌△BFE(ASA),
∴CE=EF,
∵∠BAC=90°,CE⊥BD,
∴∠ACF+∠F=90°,∠ABD+∠F=90°,
∴∠ABD=∠ACF,
在△ABD和△ACF中,
,
∴△ABD≌△ACF(ASA),
∴BD=CF,
∵CF=CE+EF=2CE,
∴BD=2CE=8,
∴CE=4.
故答案为:4.
15.解:∵BA⊥AC,
∴∠A=90°,
∵CD∥AB,
∴∠DCE=90°,
∵BC⊥DE,
∴∠DCB+∠D=90°,
∵∠DCB+∠BCA=90°,
∴∠BCA=∠D,
在△ABC和△CED中
,
∴△ABC≌△CED(AAS),
∴AB=CE=2,AC=CD=6,
∴AE=AC﹣CE=6﹣2=4.
故答案为4.
16.解:(1)∵∠ACB=∠DCE=60°,CA=CB,CD=CE,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS),
∴∠CAD=∠CBE,
∵∠CFA=∠BFE,
∴∠AEB=∠ACF=60°.
(2)同理可证△ACD≌△BCE,
∴∠CAF=∠CBE,
∵∠CBE=∠BAE,
∴∠CAF=∠BAE,
∴AF平分∠CAB,
∵FC⊥AC,CF=2,
∴点F到AB的距离=CF=2,
∴S△ABF=?AB?CF=×8×2=8.
17.解:(1)如图1,
∵BD⊥直线l,CE⊥直线l,
∴∠BDA=∠CEA=90°,
∵∠BAC=90°,
∴∠BAD+∠CAE=90°
∵∠BAD+∠ABD=90°,
∴∠CAE=∠ABD
在△ADB和△CEA中,
,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE;
(2)DE=BD+CE.
如图2,
证明如下:
∵∠BDA=∠BAC=α,
∴∠DBA+∠BAD=∠BAD+∠CAE=180°﹣α,
∴∠DBA=∠CAE,
在△ADB和△CEA中.
.
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE
(3)如图3,
过E作EM⊥HI于M,GN⊥HI的延长线于N.
∴∠EMI=GNI=90°
由(1)和(2)的结论可知EM=AH=GN
∴EM=GN
在△EMI和△GNI中,
,
∴△EMI≌△GNI(AAS),
∴EI=GI,
∴I是EG的中点.
18.
(1)AM+BN=MN,
证明:延长CB到E,使BE=AM,
∵∠A=∠CBD=90°,
∴∠A=∠EBD=90°,
在△DAM和△DBE中
,
∴△DAM≌△DBE,
∴∠BDE=∠MDA,DM=DE,
∵∠MDN=∠ADC=60°,
∴∠ADM=∠NDC,
∴∠BDE=∠NDC,
∴∠MDN=∠NDE,
在△MDN和△EDN中
,
∴△MDN≌△EDN,
∴MN=NE,
∵NE=BE+BN=AM+BN,
∴AM+BN=MN.
(2)AM+BN=MN,
证明:延长CB到E,使BE=AM,连接DE,
∵∠A=∠CBD=90°,
∴∠A=∠DBE=90°,
∵∠CDA+∠ACD=90°,∠MDN+∠ACD=90°,
∴∠MDN=∠CDA,
∵∠MDN=∠BDC,
∴∠MDA=∠CDN,∠CDM=∠NDB,
在△DAM和△DBE中
,
∴△DAM≌△DBE,
∴∠BDE=∠MDA=∠CDN,DM=DE,
∵∠MDN+∠ACD=90°,∠ACD+∠ADC=90°,
∴∠NDM=∠ADC=∠CDB,
∴∠ADM=∠CDN=∠BDE,
∵∠CDM=∠NDB
∴∠MDN=∠NDE,
在△MDN和△EDN中
,
∴△MDN≌△EDN,
∴MN=NE,
∵NE=BE+BN=AM+BN,
∴AM+BN=MN.
(3)BN﹣AM=MN,
证明:在CB截取BE=AM,连接DE,
∵∠CDA+∠ACD=90°,∠MDN+∠ACD=90°,
∴∠MDN=∠CDA,
∵∠ADN=∠ADN,
∴∠MDA=∠CDN,
∵∠B=∠CAD=90°,
∴∠B=∠DAM=90°,
在△DAM和△DBE中
,
∴△DAM≌△DBE,
∴∠BDE=∠ADM=∠CDN,DM=DE,
∵∠ADC=∠BDC=∠MDN,
∴∠MDN=∠EDN,
在△MDN和△EDN中
,
∴△MDN≌△EDN,
∴MN=NE,
∵NE=BN﹣BE=BN﹣AM,
∴BN﹣AM=MN.
19.(1)结论:AP=AQ,AP⊥AQ
证明:∵BD、CE是△ABC的高,
∴BD⊥AC,CE⊥AB,
∴∠1+∠CAB=90°,∠2+∠CAB=90°,
∴∠1=∠2,
在△QAC和△APB中,
,
∴△QAC≌△APB(SAS),
∴AQ=AP,∠QAC=∠P,
而∠DAP+∠P=90°,
∴∠DAP+∠QAC=90°,
即∠QAP=90°,
∴AQ⊥AP;
即AP=AQ,AP⊥AQ;
(2)上述结论成立,理由如下:
如图所示:
∵BD、CE是△ABC的高,
∴BD⊥AC,CE⊥AB,
∴∠1+∠CAE=90°,∠2+∠DAB=90°,
∵∠CAE=∠DAB,
∴∠1=∠2,
在△QAC和△APB中,
,
∴△QAC≌△APB(SAS),
∴AQ=AP,∠QAC=∠P,
∵∠PDA=90°,
∴∠P+∠PAD=90°,
∴∠QAC+∠PAD=90°,
∴∠QAP=90°,
∴AQ⊥AP,
即AP=AQ,AP⊥AQ.
20.解:(1)BD=AC,BD⊥AC,
理由:延长BD交AC于F.
∵AE⊥BC,
∴∠AEB=∠AEC=90°,
在△BED和△AEC中,
,
∴△BED≌△AEC(SAS),
∴BD=AC,∠DBE=∠CAE,
∵∠BED=90°,
∴∠EBD+∠BDE=90°,
∵∠BDE=∠ADF,
∴∠ADF+∠CAE=90°,
∴∠AFD=180°﹣90°=90°,
∴BD⊥AC;
(2)结论不发生变化,
理由是:设AC与DE相交于点O,
∵∠BEA=∠DEC=90°,
∴∠BEA+∠AED=∠DEC+∠AED,
∴∠BED=∠AEC,
在△BED和△AEC中,
,
∴△BED≌△AEC(SAS),
∴BD=AC,∠BDE=∠ACE,
∵∠DEC=90°,
∴∠ACE+∠EOC=90°,
∵∠EOC=∠DOF,
∴∠BDE+∠DOF=90°,
∴∠DFO=180°﹣90°=90°,
∴BD⊥AC.
21.(1)证明:∵∠BAC=∠DAE,
∴∠BAC﹣∠BAE=∠DAE﹣∠BAE,
即∠DAB=∠EAC,
又∵AB=AC,AD=AE,
∴△DAB≌△EAC(SAS),
∴BD=CE,
∴BC=BE+CE=BD+BE;
(2)解:(1)的结论不成立,成立的结论是BC=BD﹣BE.
证明:∵∠BAC=∠DAE,
∴∠BAC+∠EAB=∠DAE+∠EAB,
即∠DAB=∠EAC,
又∵AB=AC,AD=AE,
∴△DAB≌△EAC(SAS),
∴BD=CE,
∴BC=CE﹣BE=BD﹣BE.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
