人教版数学八年级上册12.3 角的平分线的性质课后培优(word解析版)
文档属性
| 名称 | 人教版数学八年级上册12.3 角的平分线的性质课后培优(word解析版) |  | |
| 格式 | docx | ||
| 文件大小 | 624.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-30 19:01:07 | ||
图片预览



文档简介
12.3 角的平分线的性质
一、单选题
1.false内一点false到三边距离相等,则点false一定是false( )
A.三条角平分线的交点 B.三边垂直平分线的交点
C.三条高的交点 D.三条中线的交点
2.如图,点false是false内一点,PD⊥BC,PE⊥AC,PF⊥AB,且false,则点false是( )
A.false三边垂直平分线的交点 B.false三条角平分线的交点
C.false三条高所在直线的交点 D.false三条中线的交点
3.如图,AD是△ABC的角平分线,DF⊥AB于点F,且DE=DG,S△ADG=24,S△AED=18,则△DEF的面积为( )
A.2 B.3 C.4 D.6
4.如图,false中,false,false平分false,交false于点false,false,false,则false的长为( )
A.4 B.8 C.3 D.6
5.如图,四边形false中,false,与false、false相邻的两外角平分线交于点E,若false,则false的度数为( )
A.45° B.60° C.40° D.50°
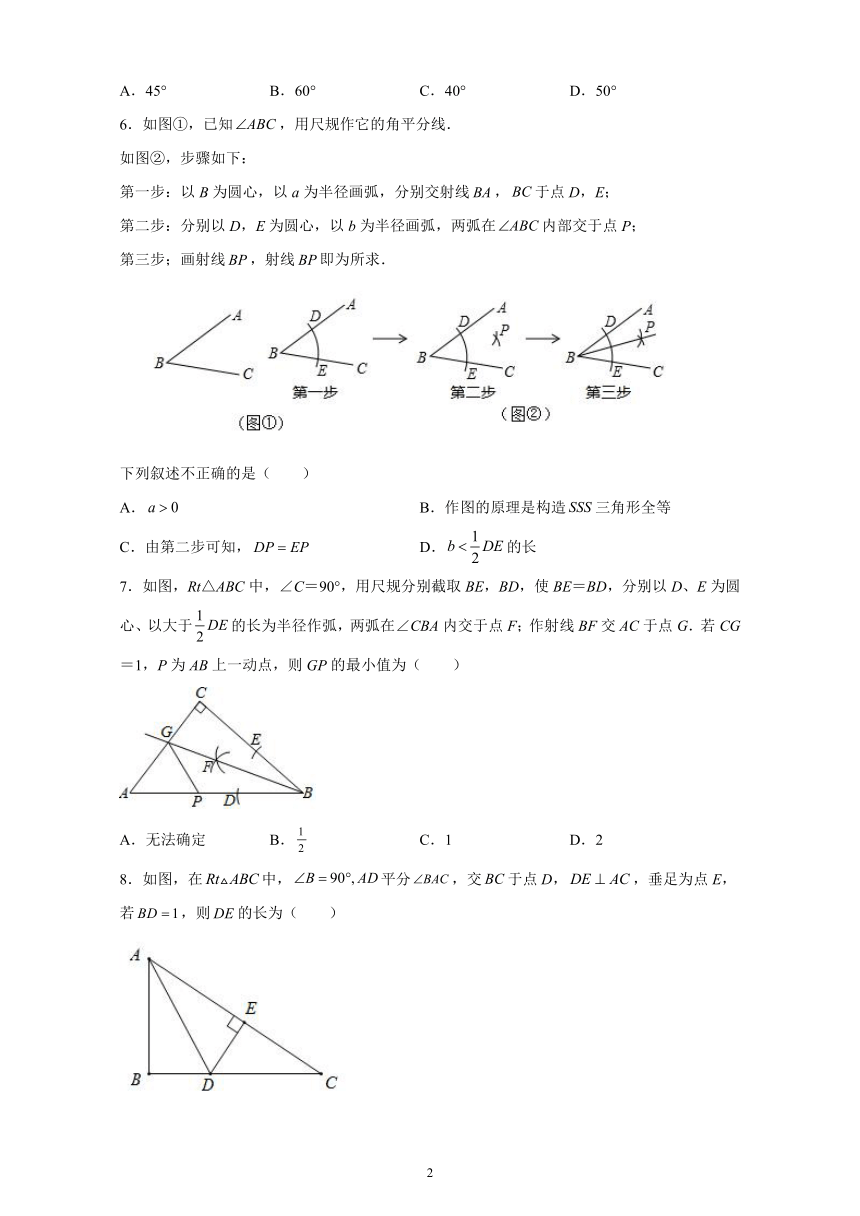
6.如图①,已知false,用尺规作它的角平分线.
如图②,步骤如下:
第一步:以B为圆心,以a为半径画弧,分别交射线false,false于点D,E;
第二步:分别以D,E为圆心,以b为半径画弧,两弧在false内部交于点P;
第三步;画射线false,射线false即为所求.
下列叙述不正确的是( )
A.false B.作图的原理是构造false三角形全等
C.由第二步可知,false D.false的长
7.如图,Rt△ABC中,∠C=90°,用尺规分别截取BE,BD,使BE=BD,分别以D、E为圆心、以大于false的长为半径作弧,两弧在∠CBA内交于点F;作射线BF交AC于点G.若CG=1,P为AB上一动点,则GP的最小值为( )
A.无法确定 B.false C.1 D.2
8.如图,在false中,false平分false,交false于点D,false,垂足为点E,若false,则false的长为( )
A.false B.1 C.2 D.6
9.如图,四边形ABCD中,对角线AD平分∠BAC,false,false,则∠ADB的度数为( )
A.54° B.50° C.48° D.46°
10.如图,直线l1、l2、l3表示三条相互交叉的公路,现要建一个货物中转站,要求它的三条公路的距离相等,则可供选择的地址有( )
A.一处 B.二处 C.三处 D.四处
11.如图,在false中,false的外角平分线与false的外角平分线相交于点false.则下列结论正确的是( )
A.false平分false B.false平分false C.false平分false D.false
12.如图,用一把长方形直尺的一边压住射线OB,再用另一把完全相同的长方形直尺的一边压住射线OA,两把直尺的另一边交于点P,则射线OP就是∠BOA的平分线的依据是( )
A.等腰三角形中线、角平分线、高线三线合一
B.三角形三条角平分线的交点到三条边的距离相等
C.角平分线上的点到这个角的两边的距离相等
D.在角的内部,到角两边距离相等的点在这个角的平分线上
二、填空题
13.如图,false平分false,false在false上,false于false,false于false.若false,则false____false.
14.如图,在false中,false,利用尺规在false,false上分别截取false;分别以点false,false为圆心,以大于false的长为半径作弧,两弧在false内部交于点false;作射线false交false于点false.若false,点false为线段false上的一动点,则false的最小值是______.
15.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于falseMN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是_______.
16.如图,在false中,false和false的平分线交于点false,得false;false和false的平分线交于点false,得false;……false和false的平分线交于点false,则false________度.
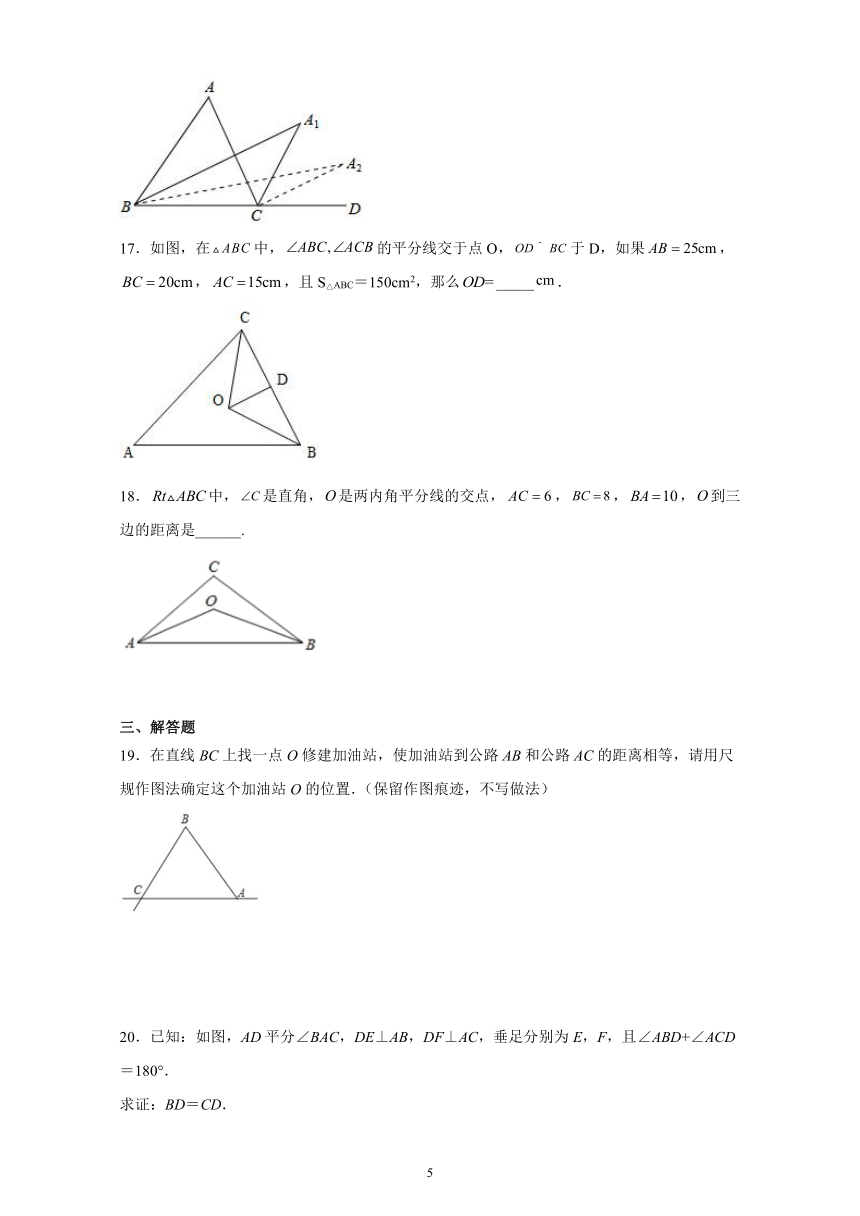
17.如图,在false中,false的平分线交于点O,false于D,如果false,false,false,且S△ABC=150cm2,那么false_____false.
18.false中,false是直角,false是两内角平分线的交点,false,false,false,false到三边的距离是______.
三、解答题
19.在直线BC上找一点O修建加油站,使加油站到公路AB和公路AC的距离相等,请用尺规作图法确定这个加油站O的位置.(保留作图痕迹,不写做法)
20.已知:如图,AD平分∠BAC,DE⊥AB,DF⊥AC,垂足分别为E,F,且∠ABD+∠ACD=180°.
求证:BD=CD.
21.如图所示,已知BE⊥AC于E,CF⊥AB于F,BE、CF相交于点D,若BF=CE,求证:AD平分∠BAC.
22.如图,在false中,false平分false,false,false于点false,点false在false上,false.
(1)求证:false;
(2)若false,false,求false的长.
23.如图,CA平分∠BCD,AB=AD,AE⊥BC,AF⊥CD,垂足分别为E、F.
(1)若∠ABE=60°,求∠CDA的大小;
(2)若AE=2,BE=1,CD=3,求四边形AECD的面积.
参考答案
1.A
解:∵点P到三边距离相等,
∴点P一定在三条角平分线的交点上,
故选:A.
2.B
解:连接PA、PB、PC.
∵PD=PF,
∴PB是∠ABC的角平分线,
同理PA、PC分别是∠BAC,∠ACB的角平分线,
故P是△ABC角平分线交点,
故选:B.
3.B
解:过点D作DH⊥AC于H,
∵AD是△ABC的角平分线,DF⊥AB,DH⊥AC,
∴DH=DF,
在Rt△DEF和Rt△DGH中,
false,
∴Rt△DEF≌Rt△DGH(HL),
∴△DEF的面积=△DGH的面积,
设△DEF的面积=△DGH的面积=S,
同理可证,Rt△ADF≌Rt△ADH,
∴△ADF的面积=△ADH的面积,
∴24-S=18+S,
解得,S=3,
故选:B.
4.C
解:如图,过点D作DE⊥AB于E,
∵∠C=90°,AD平分∠BAC,
∴DE=CD,
∴S△ABD=falseAB?DE=false×18?DE=27,
解得:DE=3,
∴CD=3.
故选:C.
5.C
解:如图,连接false并延长,
∵false,false,
∴false,
∵false、false相邻的两外角平分线交于点false,
∴false,
∵false,false,
即false
∴false.
故选:false.
6.D
解:A、∵以a为半径画弧,∴false,故正确
B、根据作图步骤可知BD=BE,PD=PE,BP=BP,∴△BDP≌△BEP(SSS),故正确
C、∵分别以D,E为圆心,以b为半径画弧,两弧在false内部交于点P,∴false,故正确
D、分别以D,E为圆心,以b为半径画弧,其中false,否则两个圆弧没有交点,故错误
故选:D
7.C
解:如图,过点G作GH⊥AB于H.
由作图可知,GB平分∠ABC,
∵GH⊥BA,GC⊥BC,
∴GH=GC=1,
根据垂线段最短可知,GP的最小值为1,
故选:C.
8.B
解:∵false,∴false,又∵false平分false,false,∴由角平分线的性质得false.
故选:B
9.C
解:如图所示,过false作false于false,false于false,false于false,
false平分false,false于false,false于false,
false,
,
,
false平分false,
又false于false,false于false,
false,
false,
false平分false,
,
false平分false,
false,
,
故选:C.
10.D
解:如图,作直线l1、l2、l3所围成的三角形的外角平分线和内角平分线,外角平分线相交于点P2、P3、P4,内角平分线相交于点P1,根据角平分线的性质可得到这4个点到三条公路的距离分别相等.
故选:D.
11.B
解:过false点分别作false、false、false的垂线,垂足分别为false、false、false,
false、false外角的平分线相交于点false,
false,false,
false,
false平分false.
故选:false.
12.D
解:如图所示:过两把直尺的交点P作PE⊥BO,PF⊥AO,
∵两把完全相同的长方形直尺的宽度相等,
∴PE=PF,
∴OP平分∠AOB(在角的内部,到角的两边的距离相等的点在这个角的平分线上),
故选:D.
13.3
解:∵OC平分∠AOB,点P在OC上,且PD⊥OA于D,PE⊥OB于E,PD=3cm,
∴PE=PD=3.
故答案为:3.
14.2
解:如图,过点F作FG⊥AB于G.
由作图可知,FB平分∠ABC,
∵GF⊥BA,FC⊥BC,
∴GF=FC=2,
根据垂线段最短可知,HF的最小值为2,
故答案为:2.
15.30
解:作false于E,如图,
由作法得AP平分∠BAC,
∴false,
∴△ABD的面积=false.
故答案为:30.
16.false
解:∵false和false的平分线交于点false,
∴false,
又∵false,
∴false,
∵false,
∴false;
同理:false;
false;
……
按照这个规律可得:false,
故答案为:false.
17.5
解:连接OA,过点O分别作AC,AB的垂线,垂足分别为E、F,
∵∠ABC,∠ACB的平分线交于点O,OD⊥BC于D,
∴OD=OE=OF,
∴S△ABC=S△AOB+S△BOC+S△AOC=falseAB?OF+falseBC?OD+falseAC?OE=falseOD(AB+BC+AC)=false×OD×(25+20+15)=150,解得:OD=5cm.
故答案为:5.
18.2
解:过O作OD⊥AC于D,OE⊥BC于E,OF⊥AB于F,连接OC,
∵O为∠A、∠B的平分线的交点,
∴OD=OF,OE=OF,
∴OD=OE=OF,
设OD=OE=OF=R,
∵S△ACB=S△AOC+S△BCO+S△ABO,
则false×6×8=false×6R+false×8R+false×10R,
解得R=2,
即OD=OE=OF=2,
∴点O到三边的距离为2,
故答案为:2.
19.见解析
解:∵公路AB和公路AC是∠BAC的两边,
∴根据∠BAC平分线上点性质,使加油站到公路AB和公路AC的距离相等, 可得加油站在∠BAC平分线上,
又∵在直线BC上找一点O修建加油站,
∴∠BAC的平分线与BC的交点满足条件,
以点A为圆心,任意长为半径,与角的两边交于两点,再以这两点为圆心,大于这两点距离的一半为半径画弧,两弧交于一点,过A与这点作射线,交BC于O,
则点O为所求.
20.见解析.
∵AD平分∠BAC,且DE⊥AB,DF⊥AC,
∴DE=DF,∠BED=∠CFD=90° ,
∵∠ABD+∠ACD=180°,且∠ABD+∠EBD=180° ,
∴∠EBD=∠ACD ,
在△BED和△CFD中
false
∴△BED≌△CFD(AAS) ,
∴BD=CD.
21.见解析
解:证明:false,false,
false,
在false和false中
false
false,
false,
false,false,
false平分false.
22.(1)见解析;(2)3
解:(1)证明:∵AD平分∠BAC,∠C=90°,DE⊥AB于E,
∴DE=DC.
在Rt△CDF与Rt△EDB中,
false,
∴Rt△CDF≌Rt△EDB(HL),
∴CF=EB.
(2)设CF=x,则AE=14-x,
∵AD平分∠BAC,DE⊥AB,
∴CD=DE.
在Rt△ACD与Rt△AED中,
false,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,即8+x=14-x,
解得x=3,即CF=3.
23.(1)120°;(2)7
解:(1)false平分false,false,false,false
false,false,
在Rt△AFD和Rt△AEB中,
false,
∴Rt△AFD≌Rt△AEB(HL),
false,
false,
false;
(2)∵Rt△AFD≌Rt△AEB,
false,false,
false,
false平分false,
false,
false,false,
false,
在Rt△AFC和Rt△AEC中,
false,
∴Rt△AFC≌Rt△AEC(HL),
false,
false四边形false的面积false.
一、单选题
1.false内一点false到三边距离相等,则点false一定是false( )
A.三条角平分线的交点 B.三边垂直平分线的交点
C.三条高的交点 D.三条中线的交点
2.如图,点false是false内一点,PD⊥BC,PE⊥AC,PF⊥AB,且false,则点false是( )
A.false三边垂直平分线的交点 B.false三条角平分线的交点
C.false三条高所在直线的交点 D.false三条中线的交点
3.如图,AD是△ABC的角平分线,DF⊥AB于点F,且DE=DG,S△ADG=24,S△AED=18,则△DEF的面积为( )
A.2 B.3 C.4 D.6
4.如图,false中,false,false平分false,交false于点false,false,false,则false的长为( )
A.4 B.8 C.3 D.6
5.如图,四边形false中,false,与false、false相邻的两外角平分线交于点E,若false,则false的度数为( )
A.45° B.60° C.40° D.50°
6.如图①,已知false,用尺规作它的角平分线.
如图②,步骤如下:
第一步:以B为圆心,以a为半径画弧,分别交射线false,false于点D,E;
第二步:分别以D,E为圆心,以b为半径画弧,两弧在false内部交于点P;
第三步;画射线false,射线false即为所求.
下列叙述不正确的是( )
A.false B.作图的原理是构造false三角形全等
C.由第二步可知,false D.false的长
7.如图,Rt△ABC中,∠C=90°,用尺规分别截取BE,BD,使BE=BD,分别以D、E为圆心、以大于false的长为半径作弧,两弧在∠CBA内交于点F;作射线BF交AC于点G.若CG=1,P为AB上一动点,则GP的最小值为( )
A.无法确定 B.false C.1 D.2
8.如图,在false中,false平分false,交false于点D,false,垂足为点E,若false,则false的长为( )
A.false B.1 C.2 D.6
9.如图,四边形ABCD中,对角线AD平分∠BAC,false,false,则∠ADB的度数为( )
A.54° B.50° C.48° D.46°
10.如图,直线l1、l2、l3表示三条相互交叉的公路,现要建一个货物中转站,要求它的三条公路的距离相等,则可供选择的地址有( )
A.一处 B.二处 C.三处 D.四处
11.如图,在false中,false的外角平分线与false的外角平分线相交于点false.则下列结论正确的是( )
A.false平分false B.false平分false C.false平分false D.false
12.如图,用一把长方形直尺的一边压住射线OB,再用另一把完全相同的长方形直尺的一边压住射线OA,两把直尺的另一边交于点P,则射线OP就是∠BOA的平分线的依据是( )
A.等腰三角形中线、角平分线、高线三线合一
B.三角形三条角平分线的交点到三条边的距离相等
C.角平分线上的点到这个角的两边的距离相等
D.在角的内部,到角两边距离相等的点在这个角的平分线上
二、填空题
13.如图,false平分false,false在false上,false于false,false于false.若false,则false____false.
14.如图,在false中,false,利用尺规在false,false上分别截取false;分别以点false,false为圆心,以大于false的长为半径作弧,两弧在false内部交于点false;作射线false交false于点false.若false,点false为线段false上的一动点,则false的最小值是______.
15.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于falseMN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是_______.
16.如图,在false中,false和false的平分线交于点false,得false;false和false的平分线交于点false,得false;……false和false的平分线交于点false,则false________度.
17.如图,在false中,false的平分线交于点O,false于D,如果false,false,false,且S△ABC=150cm2,那么false_____false.
18.false中,false是直角,false是两内角平分线的交点,false,false,false,false到三边的距离是______.
三、解答题
19.在直线BC上找一点O修建加油站,使加油站到公路AB和公路AC的距离相等,请用尺规作图法确定这个加油站O的位置.(保留作图痕迹,不写做法)
20.已知:如图,AD平分∠BAC,DE⊥AB,DF⊥AC,垂足分别为E,F,且∠ABD+∠ACD=180°.
求证:BD=CD.
21.如图所示,已知BE⊥AC于E,CF⊥AB于F,BE、CF相交于点D,若BF=CE,求证:AD平分∠BAC.
22.如图,在false中,false平分false,false,false于点false,点false在false上,false.
(1)求证:false;
(2)若false,false,求false的长.
23.如图,CA平分∠BCD,AB=AD,AE⊥BC,AF⊥CD,垂足分别为E、F.
(1)若∠ABE=60°,求∠CDA的大小;
(2)若AE=2,BE=1,CD=3,求四边形AECD的面积.
参考答案
1.A
解:∵点P到三边距离相等,
∴点P一定在三条角平分线的交点上,
故选:A.
2.B
解:连接PA、PB、PC.
∵PD=PF,
∴PB是∠ABC的角平分线,
同理PA、PC分别是∠BAC,∠ACB的角平分线,
故P是△ABC角平分线交点,
故选:B.
3.B
解:过点D作DH⊥AC于H,
∵AD是△ABC的角平分线,DF⊥AB,DH⊥AC,
∴DH=DF,
在Rt△DEF和Rt△DGH中,
false,
∴Rt△DEF≌Rt△DGH(HL),
∴△DEF的面积=△DGH的面积,
设△DEF的面积=△DGH的面积=S,
同理可证,Rt△ADF≌Rt△ADH,
∴△ADF的面积=△ADH的面积,
∴24-S=18+S,
解得,S=3,
故选:B.
4.C
解:如图,过点D作DE⊥AB于E,
∵∠C=90°,AD平分∠BAC,
∴DE=CD,
∴S△ABD=falseAB?DE=false×18?DE=27,
解得:DE=3,
∴CD=3.
故选:C.
5.C
解:如图,连接false并延长,
∵false,false,
∴false,
∵false、false相邻的两外角平分线交于点false,
∴false,
∵false,false,
即false
∴false.
故选:false.
6.D
解:A、∵以a为半径画弧,∴false,故正确
B、根据作图步骤可知BD=BE,PD=PE,BP=BP,∴△BDP≌△BEP(SSS),故正确
C、∵分别以D,E为圆心,以b为半径画弧,两弧在false内部交于点P,∴false,故正确
D、分别以D,E为圆心,以b为半径画弧,其中false,否则两个圆弧没有交点,故错误
故选:D
7.C
解:如图,过点G作GH⊥AB于H.
由作图可知,GB平分∠ABC,
∵GH⊥BA,GC⊥BC,
∴GH=GC=1,
根据垂线段最短可知,GP的最小值为1,
故选:C.
8.B
解:∵false,∴false,又∵false平分false,false,∴由角平分线的性质得false.
故选:B
9.C
解:如图所示,过false作false于false,false于false,false于false,
false平分false,false于false,false于false,
false,
,
,
false平分false,
又false于false,false于false,
false,
false,
false平分false,
,
false平分false,
false,
,
故选:C.
10.D
解:如图,作直线l1、l2、l3所围成的三角形的外角平分线和内角平分线,外角平分线相交于点P2、P3、P4,内角平分线相交于点P1,根据角平分线的性质可得到这4个点到三条公路的距离分别相等.
故选:D.
11.B
解:过false点分别作false、false、false的垂线,垂足分别为false、false、false,
false、false外角的平分线相交于点false,
false,false,
false,
false平分false.
故选:false.
12.D
解:如图所示:过两把直尺的交点P作PE⊥BO,PF⊥AO,
∵两把完全相同的长方形直尺的宽度相等,
∴PE=PF,
∴OP平分∠AOB(在角的内部,到角的两边的距离相等的点在这个角的平分线上),
故选:D.
13.3
解:∵OC平分∠AOB,点P在OC上,且PD⊥OA于D,PE⊥OB于E,PD=3cm,
∴PE=PD=3.
故答案为:3.
14.2
解:如图,过点F作FG⊥AB于G.
由作图可知,FB平分∠ABC,
∵GF⊥BA,FC⊥BC,
∴GF=FC=2,
根据垂线段最短可知,HF的最小值为2,
故答案为:2.
15.30
解:作false于E,如图,
由作法得AP平分∠BAC,
∴false,
∴△ABD的面积=false.
故答案为:30.
16.false
解:∵false和false的平分线交于点false,
∴false,
又∵false,
∴false,
∵false,
∴false;
同理:false;
false;
……
按照这个规律可得:false,
故答案为:false.
17.5
解:连接OA,过点O分别作AC,AB的垂线,垂足分别为E、F,
∵∠ABC,∠ACB的平分线交于点O,OD⊥BC于D,
∴OD=OE=OF,
∴S△ABC=S△AOB+S△BOC+S△AOC=falseAB?OF+falseBC?OD+falseAC?OE=falseOD(AB+BC+AC)=false×OD×(25+20+15)=150,解得:OD=5cm.
故答案为:5.
18.2
解:过O作OD⊥AC于D,OE⊥BC于E,OF⊥AB于F,连接OC,
∵O为∠A、∠B的平分线的交点,
∴OD=OF,OE=OF,
∴OD=OE=OF,
设OD=OE=OF=R,
∵S△ACB=S△AOC+S△BCO+S△ABO,
则false×6×8=false×6R+false×8R+false×10R,
解得R=2,
即OD=OE=OF=2,
∴点O到三边的距离为2,
故答案为:2.
19.见解析
解:∵公路AB和公路AC是∠BAC的两边,
∴根据∠BAC平分线上点性质,使加油站到公路AB和公路AC的距离相等, 可得加油站在∠BAC平分线上,
又∵在直线BC上找一点O修建加油站,
∴∠BAC的平分线与BC的交点满足条件,
以点A为圆心,任意长为半径,与角的两边交于两点,再以这两点为圆心,大于这两点距离的一半为半径画弧,两弧交于一点,过A与这点作射线,交BC于O,
则点O为所求.
20.见解析.
∵AD平分∠BAC,且DE⊥AB,DF⊥AC,
∴DE=DF,∠BED=∠CFD=90° ,
∵∠ABD+∠ACD=180°,且∠ABD+∠EBD=180° ,
∴∠EBD=∠ACD ,
在△BED和△CFD中
false
∴△BED≌△CFD(AAS) ,
∴BD=CD.
21.见解析
解:证明:false,false,
false,
在false和false中
false
false,
false,
false,false,
false平分false.
22.(1)见解析;(2)3
解:(1)证明:∵AD平分∠BAC,∠C=90°,DE⊥AB于E,
∴DE=DC.
在Rt△CDF与Rt△EDB中,
false,
∴Rt△CDF≌Rt△EDB(HL),
∴CF=EB.
(2)设CF=x,则AE=14-x,
∵AD平分∠BAC,DE⊥AB,
∴CD=DE.
在Rt△ACD与Rt△AED中,
false,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,即8+x=14-x,
解得x=3,即CF=3.
23.(1)120°;(2)7
解:(1)false平分false,false,false,false
false,false,
在Rt△AFD和Rt△AEB中,
false,
∴Rt△AFD≌Rt△AEB(HL),
false,
false,
false;
(2)∵Rt△AFD≌Rt△AEB,
false,false,
false,
false平分false,
false,
false,false,
false,
在Rt△AFC和Rt△AEC中,
false,
∴Rt△AFC≌Rt△AEC(HL),
false,
false四边形false的面积false.
