湖北省安陆一中2012届高三数学第三次综合试题(文科)
文档属性
| 名称 | 湖北省安陆一中2012届高三数学第三次综合试题(文科) |  | |
| 格式 | zip | ||
| 文件大小 | 297.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-23 16:25:31 | ||
图片预览



文档简介
2012届高三数学第三次综合试题(文科)
第Ⅰ卷 (选择题 共50分)
一、选择题(本大题共10小题,每小题5分,共50分. 在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.若= ( )
A. B. C. D.
2.“a=1”是“函数的最小正周期为π”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不是必要条件
3.已知f(x)是定义在R上的奇函数,它的最小正周期为T,则的值为( )
A.0 B. C.T D.-
4.下列命题既是全称命题,又是真命题的个数是( )
(1)对数函数都是单调函数;(2)至少有一个整数,它既是能被2整除,又能被5整除;(3)对于任意的无理数x,x2是无理数;(4)存在一整数x,使得
A.1 B.2 C.3 D.4
5.已知a、b为两条不同的直线,α、β为两个不同的平面,且,则下列命题中的
假命题是( )
A.若a∥b,则α∥β B.若α⊥β,则a⊥b
C.若a、b相交,则α、β相交 D.若α、β相交,则a、b相交
6、若函数的部分图象如图所示,则的取值是 ( )
A.
B.
C.
D.
7.设x,y满足则x+y的取值范围为 ( )
A. B. C. D.
8.定义在R上的函数满足(其中是函数的导数),又则 ( )
A. B. C. D.
9.已知抛物线=2px(p>1)的焦点F恰为双曲线(a>0,b>0)的右焦点,且两曲线的交点连线过点F,则双曲线的离心率为 ( )
A. B.+1 C.2 D.2+
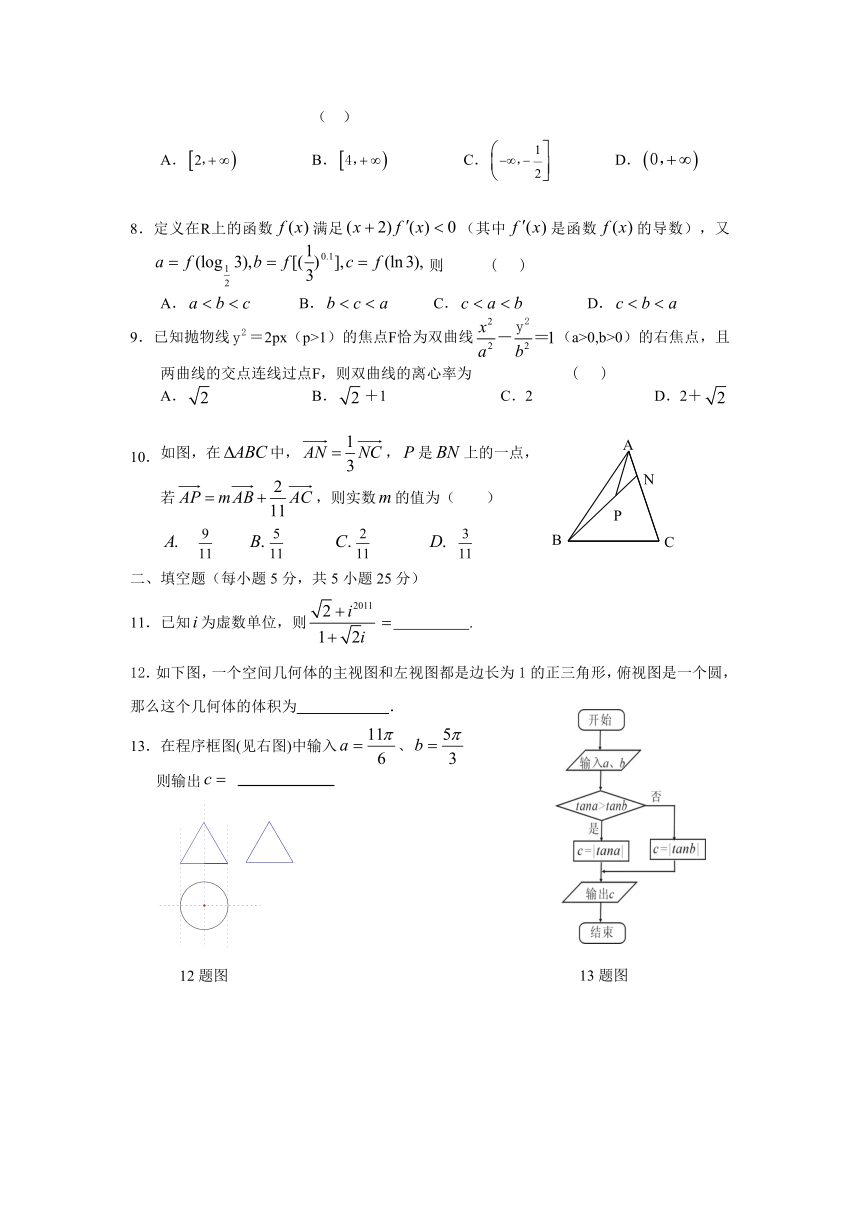
10.如图,在中,,是上的一点,
若,则实数的值为( )
二、填空题(每小题5分,共5小题25分)
11.已知为虚数单位,则 .
12.如下图,一个空间几何体的主视图和左视图都是边长为1的正三角形,俯视图是一个圆,
那么这个几何体的体积为 .
13.在程序框图(见右图)中输入、
则输出
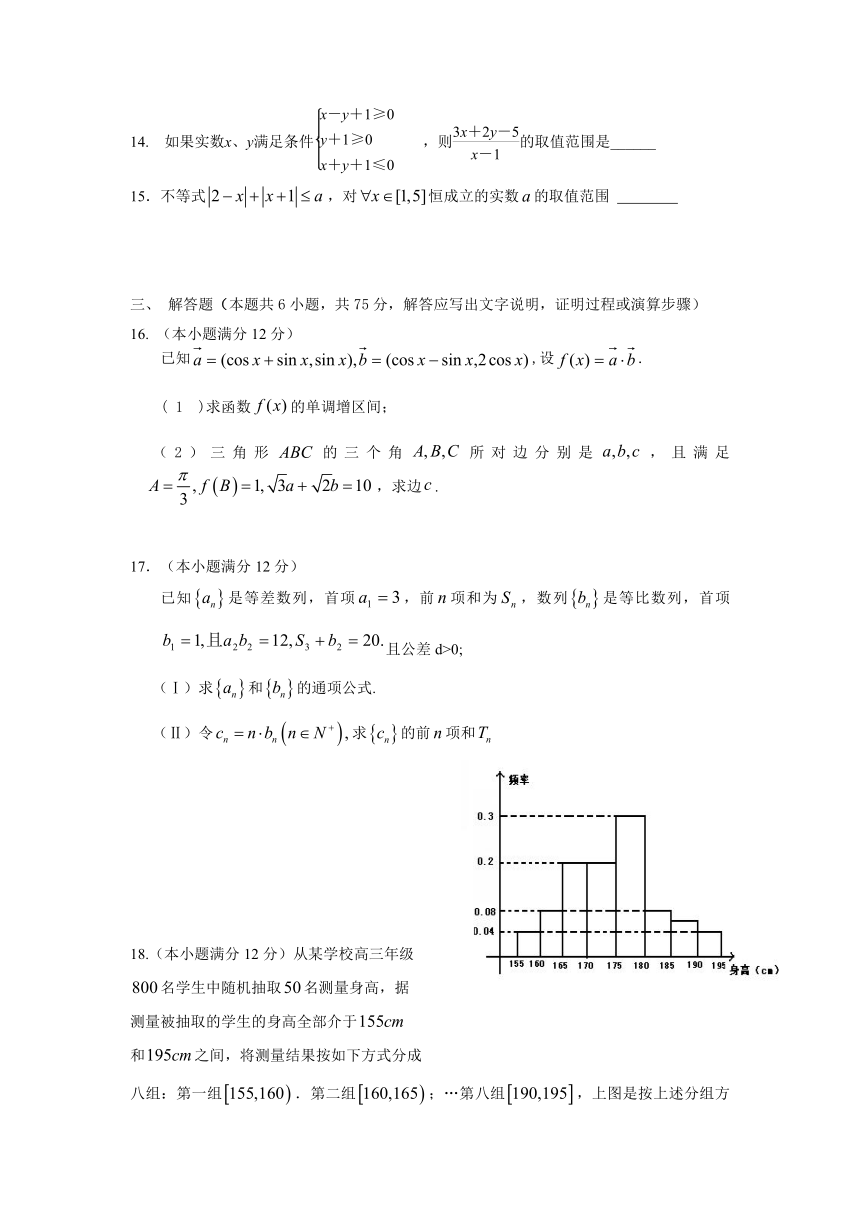
14. 如果实数x、y满足条件,则的取值范围是______
15.不等式,对恒成立的实数的取值范围
三、 解答题(本题共6小题,共75分,解答应写出文字说明,证明过程或演算步骤)
16. (本小题满分12分)
已知,设.
( 1 )求函数的单调增区间;
(2)三角形的三个角所对边分别是,且满足,求边.
17.(本小题满分12分)
已知是等差数列,首项,前项和为,数列是等比数列,首项且公差d>0;
(Ⅰ)求和的通项公式.
(Ⅱ)令求的前项和
18.(本小题满分12分)从某学校高三年级
名学生中随机抽取名测量身高,据
测量被抽取的学生的身高全部介于
和之间,将测量结果按如下方式分成
八组:第一组.第二组;…第八组,上图是按上述分组方法得到的条形图. (1)根据已知条件填写下面表格:
组别 1 2 3 4 5 6 7 8
样本数 2 4 10 10 15 4
(2)估计这所学校高三年级名学生中身高在以上(含)的人数;
(3)在样本中,若第二组有人为男生,其余为女生,第七组有人为女生,其余为男生,在第二组和第七组中各选一名同学组成实验小组,问:实验小组中恰为一男一女的概率是多少?
19. (本小题满分12分)
如图,多面体中,面为正方形,均垂直平面,
且分别为的中点.
(Ⅰ)若为的中点,证明∥平面;
(Ⅱ)求三棱锥的体积.
.
20.(本小题满分13分)
已知椭圆的中心在原点,焦点在轴上,离心率为,且经过点,直线交椭圆于不同的两点A,B.
(Ⅰ)求椭圆的方程;
(Ⅱ)求的取值范围;
(Ⅲ)若直线不过点M,试问是否为定值?
21.(本小题满分14分)
已知函数 .
(Ⅰ)当时,求证:函数在上单调递增;
(Ⅱ)若函数有三个零点,求的值.
2012届高三数学第三次综合试题(文科)
答题卡
一、选择题:本大题共有12小题,共50分)
二、填空题(共5小题,每小题5分,共25分)
11.___________________ 12.________________
13.__________________ 14.___________________
15.___________________
三、解答题(本大题共6小题,共75分,解答时应写出文字说明、证明过程或演算步骤。)
16题:(12分)
17题:(12分)
18题:(12分) (1)
组别 1 2 3 4 5 6 7 8
样本数 2 4 10 10 15 4
19题:(12分)
20题:(13分)
21题:(14分)
2012届高三数学第三次综合试题(文科)
答案
一、选择题:本大题共有12小题,共50分)
二、填空题(共5小题,每小题5分,共25分)
11.________ ___________ 12.________________
13._______ ____________ 14._______[4,7]______________
15.____ _______________
16. 解: (1) =
= ==
== ………………………………3分
由递增得:即
∴的递增区间是 。 ……………………6分
(2)由及得, ……………………8分
设,则 ……10分
所以。………12分
17:解:(Ⅰ)设公差为公比为,依题意可得:
,解得:
6分
(Ⅱ),
又,
两式作差可得:
12分
18. 解:(1)由条形图得第七组频率为.
∴第七组的人数为3人. 第八组的人数为2人,即
组别 1 2 3 4 5 6 7 8
样本数 2 4 10 10 15 4 3 2
--------4分
(2)由条形图得后三组频率为(0.08+0.06+0.04)=0.18,估计这所学校高三年级身高在180cm以上(含180cm)的人数800×0.18=144(人). ---------8分
(3)基本事件有12个,恰为一男一女的事件有共7个,因此实验小组中,恰为一男一女的概率是.---12分
19:解:(Ⅰ)取的中点,由题意知, ∥,∥,
面∥面,∥∥.
又PN∥, ∥.
∥面. 6分
(Ⅱ)由(Ⅰ)PN∥面,
,
又面,∥,
. 12分
20:解:(Ⅰ),
依题意设椭圆方程为:把点代入,得
椭圆方程为 5分
(Ⅱ)把代入椭圆方程得:,
由△可得 (8分)
(Ⅲ)设,A,B与M不重合,,
为定值0. 12分
21.解:(Ⅰ)
由于,故当时,,所以,
故函数在上单调递增 。。。。。。。。。。。。。。。。6分
(Ⅱ)当时,因为,且在R上单调递增,
故有唯一解 (10分),
所以的变化情况如下表所示:
x 0
- 0 +
递减 极小值 递增
又函数有三个零点,所以方程有三个根,
而,所以,解得 。。。。。。。。。。14分
C
A
B
N
P
13题图
12题图
题 号 1 2 3 4 5 6 7 8 9 10
答 案
题 号 1 2 3 4 5 6 7 8 9 10
答 案 A A A A D C A D B D
第Ⅰ卷 (选择题 共50分)
一、选择题(本大题共10小题,每小题5分,共50分. 在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.若= ( )
A. B. C. D.
2.“a=1”是“函数的最小正周期为π”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不是必要条件
3.已知f(x)是定义在R上的奇函数,它的最小正周期为T,则的值为( )
A.0 B. C.T D.-
4.下列命题既是全称命题,又是真命题的个数是( )
(1)对数函数都是单调函数;(2)至少有一个整数,它既是能被2整除,又能被5整除;(3)对于任意的无理数x,x2是无理数;(4)存在一整数x,使得
A.1 B.2 C.3 D.4
5.已知a、b为两条不同的直线,α、β为两个不同的平面,且,则下列命题中的
假命题是( )
A.若a∥b,则α∥β B.若α⊥β,则a⊥b
C.若a、b相交,则α、β相交 D.若α、β相交,则a、b相交
6、若函数的部分图象如图所示,则的取值是 ( )
A.
B.
C.
D.
7.设x,y满足则x+y的取值范围为 ( )
A. B. C. D.
8.定义在R上的函数满足(其中是函数的导数),又则 ( )
A. B. C. D.
9.已知抛物线=2px(p>1)的焦点F恰为双曲线(a>0,b>0)的右焦点,且两曲线的交点连线过点F,则双曲线的离心率为 ( )
A. B.+1 C.2 D.2+
10.如图,在中,,是上的一点,
若,则实数的值为( )
二、填空题(每小题5分,共5小题25分)
11.已知为虚数单位,则 .
12.如下图,一个空间几何体的主视图和左视图都是边长为1的正三角形,俯视图是一个圆,
那么这个几何体的体积为 .
13.在程序框图(见右图)中输入、
则输出
14. 如果实数x、y满足条件,则的取值范围是______
15.不等式,对恒成立的实数的取值范围
三、 解答题(本题共6小题,共75分,解答应写出文字说明,证明过程或演算步骤)
16. (本小题满分12分)
已知,设.
( 1 )求函数的单调增区间;
(2)三角形的三个角所对边分别是,且满足,求边.
17.(本小题满分12分)
已知是等差数列,首项,前项和为,数列是等比数列,首项且公差d>0;
(Ⅰ)求和的通项公式.
(Ⅱ)令求的前项和
18.(本小题满分12分)从某学校高三年级
名学生中随机抽取名测量身高,据
测量被抽取的学生的身高全部介于
和之间,将测量结果按如下方式分成
八组:第一组.第二组;…第八组,上图是按上述分组方法得到的条形图. (1)根据已知条件填写下面表格:
组别 1 2 3 4 5 6 7 8
样本数 2 4 10 10 15 4
(2)估计这所学校高三年级名学生中身高在以上(含)的人数;
(3)在样本中,若第二组有人为男生,其余为女生,第七组有人为女生,其余为男生,在第二组和第七组中各选一名同学组成实验小组,问:实验小组中恰为一男一女的概率是多少?
19. (本小题满分12分)
如图,多面体中,面为正方形,均垂直平面,
且分别为的中点.
(Ⅰ)若为的中点,证明∥平面;
(Ⅱ)求三棱锥的体积.
.
20.(本小题满分13分)
已知椭圆的中心在原点,焦点在轴上,离心率为,且经过点,直线交椭圆于不同的两点A,B.
(Ⅰ)求椭圆的方程;
(Ⅱ)求的取值范围;
(Ⅲ)若直线不过点M,试问是否为定值?
21.(本小题满分14分)
已知函数 .
(Ⅰ)当时,求证:函数在上单调递增;
(Ⅱ)若函数有三个零点,求的值.
2012届高三数学第三次综合试题(文科)
答题卡
一、选择题:本大题共有12小题,共50分)
二、填空题(共5小题,每小题5分,共25分)
11.___________________ 12.________________
13.__________________ 14.___________________
15.___________________
三、解答题(本大题共6小题,共75分,解答时应写出文字说明、证明过程或演算步骤。)
16题:(12分)
17题:(12分)
18题:(12分) (1)
组别 1 2 3 4 5 6 7 8
样本数 2 4 10 10 15 4
19题:(12分)
20题:(13分)
21题:(14分)
2012届高三数学第三次综合试题(文科)
答案
一、选择题:本大题共有12小题,共50分)
二、填空题(共5小题,每小题5分,共25分)
11.________ ___________ 12.________________
13._______ ____________ 14._______[4,7]______________
15.____ _______________
16. 解: (1) =
= ==
== ………………………………3分
由递增得:即
∴的递增区间是 。 ……………………6分
(2)由及得, ……………………8分
设,则 ……10分
所以。………12分
17:解:(Ⅰ)设公差为公比为,依题意可得:
,解得:
6分
(Ⅱ),
又,
两式作差可得:
12分
18. 解:(1)由条形图得第七组频率为.
∴第七组的人数为3人. 第八组的人数为2人,即
组别 1 2 3 4 5 6 7 8
样本数 2 4 10 10 15 4 3 2
--------4分
(2)由条形图得后三组频率为(0.08+0.06+0.04)=0.18,估计这所学校高三年级身高在180cm以上(含180cm)的人数800×0.18=144(人). ---------8分
(3)基本事件有12个,恰为一男一女的事件有共7个,因此实验小组中,恰为一男一女的概率是.---12分
19:解:(Ⅰ)取的中点,由题意知, ∥,∥,
面∥面,∥∥.
又PN∥, ∥.
∥面. 6分
(Ⅱ)由(Ⅰ)PN∥面,
,
又面,∥,
. 12分
20:解:(Ⅰ),
依题意设椭圆方程为:把点代入,得
椭圆方程为 5分
(Ⅱ)把代入椭圆方程得:,
由△可得 (8分)
(Ⅲ)设,A,B与M不重合,,
为定值0. 12分
21.解:(Ⅰ)
由于,故当时,,所以,
故函数在上单调递增 。。。。。。。。。。。。。。。。6分
(Ⅱ)当时,因为,且在R上单调递增,
故有唯一解 (10分),
所以的变化情况如下表所示:
x 0
- 0 +
递减 极小值 递增
又函数有三个零点,所以方程有三个根,
而,所以,解得 。。。。。。。。。。14分
C
A
B
N
P
13题图
12题图
题 号 1 2 3 4 5 6 7 8 9 10
答 案
题 号 1 2 3 4 5 6 7 8 9 10
答 案 A A A A D C A D B D
同课章节目录
