科学命题同步练习之23.2中心对称(含解析)
文档属性
| 名称 | 科学命题同步练习之23.2中心对称(含解析) | 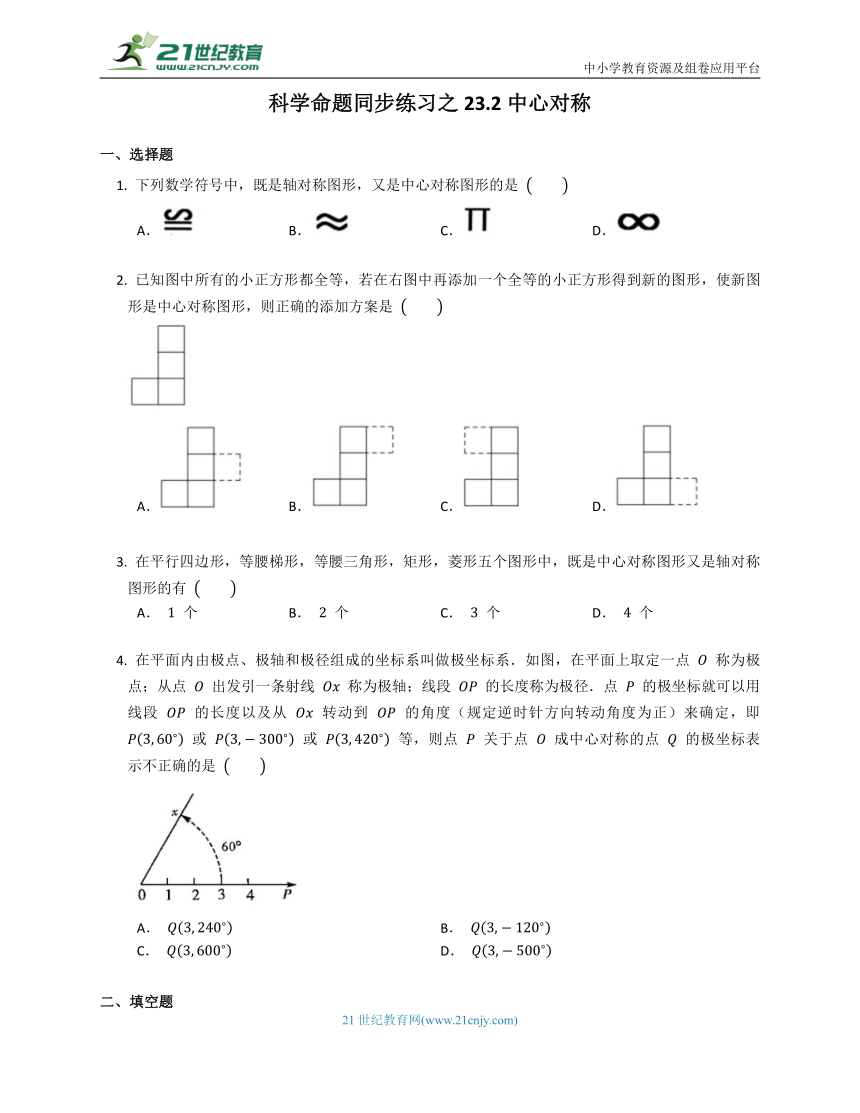 | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-30 08:52:39 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
科学命题同步练习之23.2中心对称
一、选择题
下列数学符号中,既是轴对称图形,又是中心对称图形的是
A.
B.
C.
D.
已知图中所有的小正方形都全等,若在右图中再添加一个全等的小正方形得到新的图形,使新图形是中心对称图形,则正确的添加方案是
A.
B.
C.
D.
在平行四边形,等腰梯形,等腰三角形,矩形,菱形五个图形中,既是中心对称图形又是轴对称图形的有
A.
个
B.
个
C.
个
D.
个
在平面内由极点、极轴和极径组成的坐标系叫做极坐标系.如图,在平面上取定一点
称为极点;从点
出发引一条射线
称为极轴;线段
的长度称为极径.点
的极坐标就可以用线段
的长度以及从
转动到
的角度(规定逆时针方向转动角度为正)来确定,即
或
或
等,则点
关于点
成中心对称的点
的极坐标表示不正确的是
A.
B.
C.
D.
二、填空题
如图,平行四边形
的对角线
,
交于点
,则图中成中心对称的三角形共有
对.
在一次数学社团活动上,小明设计了一个社团标识,如图所示,正方形
与折线
构成了中心对称图形,且
,
长
,
比
长
,那么
的长是
.
如图,已知
,,,
与
关于点
成中心对称,则
的长是
.
如图,是
正方形网格,把其中一个标有数字的白色小正方形涂黑,就可以使图中的黑色部分构成一个中心对称图形,则这个白色小正方形内的数字是
.
如图,数轴上表示
,
的对应点分别为
,,
点关于点
的对称点为点
,则点
所对应的数为
.
等边三角形绕它的中心至少旋转
度,才能和原图形重合.
三、解答题
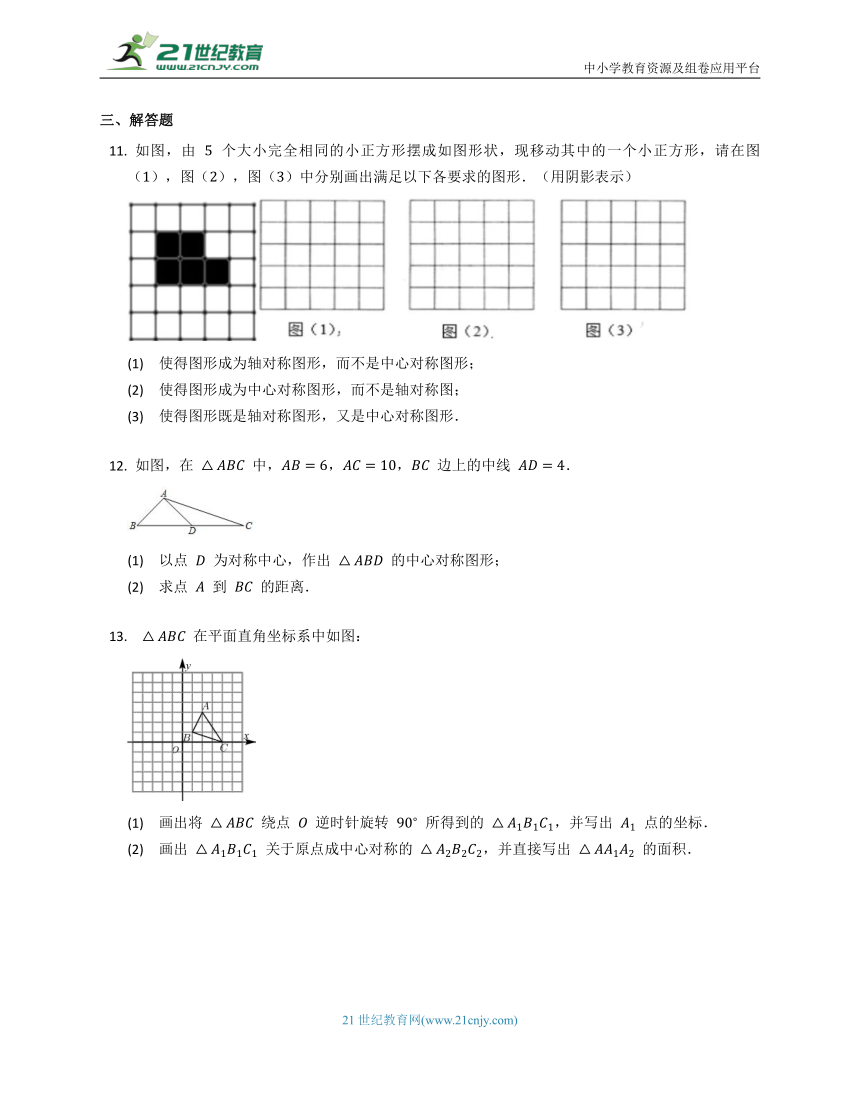
如图,由
个大小完全相同的小正方形摆成如图形状,现移动其中的一个小正方形,请在图(),图(),图()中分别画出满足以下各要求的图形.(用阴影表示)
(1)
使得图形成为轴对称图形,而不是中心对称图形;
(2)
使得图形成为中心对称图形,而不是轴对称图;
(3)
使得图形既是轴对称图形,又是中心对称图形.
如图,在
中,,,
边上的中线
.
(1)
以点
为对称中心,作出
的中心对称图形;
(2)
求点
到
的距离.
在平面直角坐标系中如图:
(1)
画出将
绕点
逆时针旋转
所得到的
,并写出
点的坐标.
(2)
画出
关于原点成中心对称的
,并直接写出
的面积.
答案
一、选择题
1.
【答案】D
【解析】A既不是轴对称图形也不是中心对称图形;
B是中心对称图形,但不是轴对称图形;
C是轴对称图形,但不是中心对称图形;
D既是轴对称图形,又是中心对称图形.
【知识点】中心对称及其性质
2.
【答案】B
【解析】A、新图形不是中心对称图形,故此选项错误;
B、新图形是中心对称图形,故此选项正确;
C、新图形不是中心对称图形,故此选项错误;
D、新图形不是中心对称图形,故此选项错误;
故选:B.
【知识点】中心对称及其性质
3.
【答案】B
【知识点】中心对称及其性质、轴对称图形
4.
【答案】D
【知识点】平面直角坐标系及点的坐标、中心对称及其性质
二、填空题
5.
【答案】
【解析】平行四边形
是中心对称图形,
根据中心对称图形的性质,对称点的连线到对称中心的距离相等,
即对称中心是对称点连线的中点,
并且中心对称图形被经过对称中心的直线平分成两个全等的图形,
据此即可判断,图中成中心对称的三角形有
和
,
与
,
与
,
和
共
对.
【知识点】中心对称及其性质
6.
【答案】
【解析】连接
,与
交于点
.
正方形
与折线
构成了中心对称图形,
,,
,
,
.
设
,则
,.
在
中,,
解得
或
(舍去),
.
【知识点】中心对称及其性质
7.
【答案】
【解析】
与
关于点
成中心对称,
,,
在
中,
的长是:.
故答案为:.
【知识点】中心对称及其性质
8.
【答案】
【解析】
【知识点】中心对称及其性质
9.
【答案】
【解析】
数轴上表示
,
对应点分别为
,,
,
设
点关于点
的对称点为点
为
,
则有
,解可得
,
故点
所对应的数为
.
【知识点】在数轴上表示实数、中心对称及其性质
10.
【答案】
【解析】由于等边三角形三角完全相同,
旋转时,只要使下一个角对准原角,就能重合,
一圈
度,除以
,就得到
度.
【知识点】中心对称及其性质
三、解答题
11.
【答案】
(1)
本题是图案设计问题,用轴对称和中心对称知识画图,设计图案,要按照题目要求,展开丰富的想象力,答案不唯一.
(2)
本题是图案设计问题,用轴对称和中心对称知识画图,设计图案,要按照题目要求,展开丰富的想象力,答案不唯一.
(3)
本题是图案设计问题,用轴对称和中心对称知识画图,设计图案,要按照题目要求,展开丰富的想象力,答案不唯一.
【知识点】中心对称及其性质、轴对称图形
12.
【答案】
(1)
如图,
为所作.
(2)
作
于
,如图.
为中线,
,而
,,
.
,.
在
中,
,,,
.
为直角三角形,.
.
在
中,.
,
,即点
到
的距离为
.
【知识点】勾股定理、中心对称及其性质
13.
【答案】
(1)
将
绕点
逆时针旋转
所得到的
如图所示;
点的坐标为
.
(2)
关于原点成中心对称的
如图所示.
.
【解析】
(2)
,
,
,
,
是等腰直角三角形,
.
【知识点】坐标平面内图形的面积、坐标平面内图形的旋转变换、中心对称及其性质
21世纪教育网(www.21cnjy.com)
科学命题同步练习之23.2中心对称
一、选择题
下列数学符号中,既是轴对称图形,又是中心对称图形的是
A.
B.
C.
D.
已知图中所有的小正方形都全等,若在右图中再添加一个全等的小正方形得到新的图形,使新图形是中心对称图形,则正确的添加方案是
A.
B.
C.
D.
在平行四边形,等腰梯形,等腰三角形,矩形,菱形五个图形中,既是中心对称图形又是轴对称图形的有
A.
个
B.
个
C.
个
D.
个
在平面内由极点、极轴和极径组成的坐标系叫做极坐标系.如图,在平面上取定一点
称为极点;从点
出发引一条射线
称为极轴;线段
的长度称为极径.点
的极坐标就可以用线段
的长度以及从
转动到
的角度(规定逆时针方向转动角度为正)来确定,即
或
或
等,则点
关于点
成中心对称的点
的极坐标表示不正确的是
A.
B.
C.
D.
二、填空题
如图,平行四边形
的对角线
,
交于点
,则图中成中心对称的三角形共有
对.
在一次数学社团活动上,小明设计了一个社团标识,如图所示,正方形
与折线
构成了中心对称图形,且
,
长
,
比
长
,那么
的长是
.
如图,已知
,,,
与
关于点
成中心对称,则
的长是
.
如图,是
正方形网格,把其中一个标有数字的白色小正方形涂黑,就可以使图中的黑色部分构成一个中心对称图形,则这个白色小正方形内的数字是
.
如图,数轴上表示
,
的对应点分别为
,,
点关于点
的对称点为点
,则点
所对应的数为
.
等边三角形绕它的中心至少旋转
度,才能和原图形重合.
三、解答题
如图,由
个大小完全相同的小正方形摆成如图形状,现移动其中的一个小正方形,请在图(),图(),图()中分别画出满足以下各要求的图形.(用阴影表示)
(1)
使得图形成为轴对称图形,而不是中心对称图形;
(2)
使得图形成为中心对称图形,而不是轴对称图;
(3)
使得图形既是轴对称图形,又是中心对称图形.
如图,在
中,,,
边上的中线
.
(1)
以点
为对称中心,作出
的中心对称图形;
(2)
求点
到
的距离.
在平面直角坐标系中如图:
(1)
画出将
绕点
逆时针旋转
所得到的
,并写出
点的坐标.
(2)
画出
关于原点成中心对称的
,并直接写出
的面积.
答案
一、选择题
1.
【答案】D
【解析】A既不是轴对称图形也不是中心对称图形;
B是中心对称图形,但不是轴对称图形;
C是轴对称图形,但不是中心对称图形;
D既是轴对称图形,又是中心对称图形.
【知识点】中心对称及其性质
2.
【答案】B
【解析】A、新图形不是中心对称图形,故此选项错误;
B、新图形是中心对称图形,故此选项正确;
C、新图形不是中心对称图形,故此选项错误;
D、新图形不是中心对称图形,故此选项错误;
故选:B.
【知识点】中心对称及其性质
3.
【答案】B
【知识点】中心对称及其性质、轴对称图形
4.
【答案】D
【知识点】平面直角坐标系及点的坐标、中心对称及其性质
二、填空题
5.
【答案】
【解析】平行四边形
是中心对称图形,
根据中心对称图形的性质,对称点的连线到对称中心的距离相等,
即对称中心是对称点连线的中点,
并且中心对称图形被经过对称中心的直线平分成两个全等的图形,
据此即可判断,图中成中心对称的三角形有
和
,
与
,
与
,
和
共
对.
【知识点】中心对称及其性质
6.
【答案】
【解析】连接
,与
交于点
.
正方形
与折线
构成了中心对称图形,
,,
,
,
.
设
,则
,.
在
中,,
解得
或
(舍去),
.
【知识点】中心对称及其性质
7.
【答案】
【解析】
与
关于点
成中心对称,
,,
在
中,
的长是:.
故答案为:.
【知识点】中心对称及其性质
8.
【答案】
【解析】
【知识点】中心对称及其性质
9.
【答案】
【解析】
数轴上表示
,
对应点分别为
,,
,
设
点关于点
的对称点为点
为
,
则有
,解可得
,
故点
所对应的数为
.
【知识点】在数轴上表示实数、中心对称及其性质
10.
【答案】
【解析】由于等边三角形三角完全相同,
旋转时,只要使下一个角对准原角,就能重合,
一圈
度,除以
,就得到
度.
【知识点】中心对称及其性质
三、解答题
11.
【答案】
(1)
本题是图案设计问题,用轴对称和中心对称知识画图,设计图案,要按照题目要求,展开丰富的想象力,答案不唯一.
(2)
本题是图案设计问题,用轴对称和中心对称知识画图,设计图案,要按照题目要求,展开丰富的想象力,答案不唯一.
(3)
本题是图案设计问题,用轴对称和中心对称知识画图,设计图案,要按照题目要求,展开丰富的想象力,答案不唯一.
【知识点】中心对称及其性质、轴对称图形
12.
【答案】
(1)
如图,
为所作.
(2)
作
于
,如图.
为中线,
,而
,,
.
,.
在
中,
,,,
.
为直角三角形,.
.
在
中,.
,
,即点
到
的距离为
.
【知识点】勾股定理、中心对称及其性质
13.
【答案】
(1)
将
绕点
逆时针旋转
所得到的
如图所示;
点的坐标为
.
(2)
关于原点成中心对称的
如图所示.
.
【解析】
(2)
,
,
,
,
是等腰直角三角形,
.
【知识点】坐标平面内图形的面积、坐标平面内图形的旋转变换、中心对称及其性质
21世纪教育网(www.21cnjy.com)
同课章节目录
