2021-2022学年 人教版(五四制)七年级数学上册 《第12章 相交线与平行线》单元练习卷(word版含解析)
文档属性
| 名称 | 2021-2022学年 人教版(五四制)七年级数学上册 《第12章 相交线与平行线》单元练习卷(word版含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 260.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-30 06:22:22 | ||
图片预览





文档简介
第12章
相交线与平行线
一.选择题
1.三条直线相交,交点最多有( )
A.1个
B.2个
C.3个
D.4个
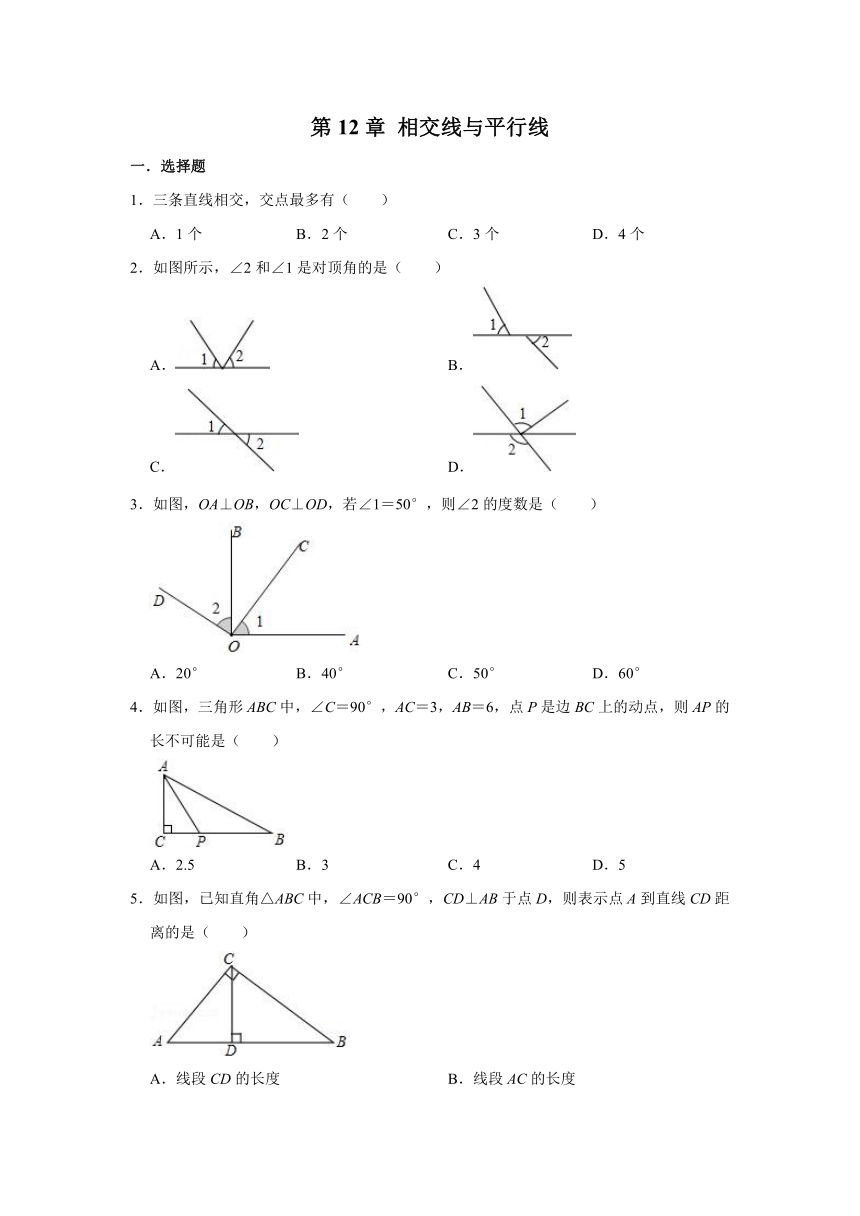
2.如图所示,∠2和∠1是对顶角的是( )
A.
B.
C.
D.
3.如图,OA⊥OB,OC⊥OD,若∠1=50°,则∠2的度数是( )
A.20°
B.40°
C.50°
D.60°
4.如图,三角形ABC中,∠C=90°,AC=3,AB=6,点P是边BC上的动点,则AP的长不可能是( )
A.2.5
B.3
C.4
D.5
5.如图,已知直角△ABC中,∠ACB=90°,CD⊥AB于点D,则表示点A到直线CD距离的是( )
A.线段CD的长度
B.线段AC的长度
C.线段AD的长度
D.线段BC的长度
6.如图,∠1和∠2不是同位角的是( )
A.
B.
C.
D.
7.如图,直线b、c被直线a所截,则∠1与∠2是( )
A.内错角
B.同位角
C.同旁内角
D.对顶角
8.同一平面内两条直线的位置关系有( )
A.相交、垂直
B.相交、平行
C.垂直、平行
D.相交、垂直、平行
9.下列结论:①平面内3条直线两两相交,共有3个交点;②在平面内,若∠AOB=40°,∠AOC=∠BOC,则∠AOC的度数为20°;③若线段AB=3,BC=2,则线段AC的长为1或5;④若∠α+∠β=180°,且∠α<∠β,则∠α的余角为(∠β﹣∠α).其中正确结论的个数有( )
A.1个
B.2个
C.3个
D.4个
10.观察图形,并阅读相关的文字:那么8条直线相交,最多可形成交点的个数是( )
A.21
B.28
C.36
D.45
二.填空题
11.如图,直线AB,CD相交于点O,OA平分∠EOC.若∠AOE=36°,则∠DOE=
°.
12.如图直线AB,CD相交于O,直线FE⊥AB于O,∠BOD=75°,则∠COF的度数为
度.
13.如图,∠1与∠2是直线
和
被直线
所截的一对
角.
14.三条直线相交,最多有
个交点.
15.如图所示,在铁路旁边有一李庄,现要建一火车站,为了使李庄人乘火车最方便(即距离最近),请你在铁路旁选一点来建火车站(位置已选好),说明理由:
.
16.若平面上4条直线两两相交且无三线共点,则共有同旁内角
对.
17.平面内有四条不同的直线两两相交,若最多有m个交点,最少有n个交点,那么(﹣n)m=
.
18.如图,在△ABC中,∠ACB=90°,CD⊥AD,垂足为点D,那么点B到直线CD的距离是线段
的长.
19.平面上不重合的四条直线,可能产生交点的个数为
个.
20.在一平面中,两条直线相交有一个交点;三条直线两两相交最多有3个交点;四条直线两两相交最多有6个交点……当相交直线的条数从2至n变化时,最多可有的交点数P与直线条数n之间的关系如下表:
直线条数n/条
2
3
4
5
6
7
8
…
最多交点个数p/个
1
3
6
10
…
…
…
…
则n与p的关系式为:
.
三.解答题
21.如图,在直角三角形ABC中,∠C=90°.
(1)画出点C到AB的最短路径CD;
(2)请指出B到AC的距离是线段
的长度.
22.如图,两直线AB,CD相交于点O,OE平分∠BOD,且∠AOC:∠AOD=3:7
(1)求∠DOE的度数;
(2)若∠EOF是直角,求∠COF的度数.
23.如图,直线AB、CD交于O点,且∠BOC=80°,OE平分∠BOC,OF为OE的反向延长线.
(1)求∠2和∠3的度数;
(2)OF平分∠AOD吗?为什么?
24.如图,点O是直线AB上一点,∠AOC=40°,OD平分∠AOC,∠COE=70°.
(1)请你说明DO⊥OE;
(2)OE平分∠BOC吗?为什么?
25.如图,点P,点Q分别代表两个村庄,直线l代表两个村庄中间的一条公路.根据居民出行的需要,计划在公路l上的某处设置一个公交站.
(1)若考虑到村庄P居住的老年人较多,计划建一个离村庄P最近的车站,请在公路l上画出车站的位置(用点M表示),依据是
;
(2)若考虑到修路的费用问题,希望车站的位置到村庄P和村庄Q的距离之和最小,请在公路l上画出车站的位置(用点N表示),依据是
.
26.平面内有不重合的4条直线,请指出这4条直线交点个数的所有情况,并画出相应的草图.
参考答案与试题解析
一.选择题(共10小题)
1.三条直线相交,交点最多有( )
A.1个
B.2个
C.3个
D.4个
【分析】根据题意画出图形可得答案.
【解答】解:如图:
,
交点最多3个,
故选:C.
2.如图所示,∠2和∠1是对顶角的是( )
A.
B.
C.
D.
【分析】根据对顶角的定义对各图形判断即可.
【解答】解:A.∠1和∠2不是对顶角,
B.∠1和∠2不是对顶角,
C.∠1和∠2是对顶角,
D.∠1和∠2不是对顶角.
3.如图,OA⊥OB,OC⊥OD,若∠1=50°,则∠2的度数是( )
A.20°
B.40°
C.50°
D.60°
【分析】先求出∠BOC,即可求出∠2.
【解答】解:∵OA⊥OB,OC⊥OD,∴∠AOB=∠COD=90°.
∠BOC=∠AOB﹣∠1=90°﹣50°=40°,
∠2=∠COD﹣∠BOC=90°﹣40°=50°.
故选:C.
4.如图,三角形ABC中,∠C=90°,AC=3,AB=6,点P是边BC上的动点,则AP的长不可能是( )
A.2.5
B.3
C.4
D.5
【分析】根据垂线段最短,可得答案.
【解答】解:由垂线段最短,得
AP≥AC=3,
故选:A.
5.如图,已知直角△ABC中,∠ACB=90°,CD⊥AB于点D,则表示点A到直线CD距离的是( )
A.线段CD的长度
B.线段AC的长度
C.线段AD的长度
D.线段BC的长度
【分析】根据点到直线的距离的概念:直线外一点到这条直线的垂线段的长度即为该点到这条直线的距离作答.
【解答】解:点A到CD的距离是线段AD的长度.
故选:C.
6.如图,∠1和∠2不是同位角的是( )
A.
B.
C.
D.
【分析】利用同位角的定义,直接分析得出即可.
【解答】解:A、∠1和∠2是同位角,故此选项不符合题意;
B、∠1和∠2是同位角,故此选项不符合题意;
C、∠1和∠2是同位角,故此选项不符合题意;
D、∠1和∠2不是同位角,故此选项符合题意;
故选:D.
7.如图,直线b、c被直线a所截,则∠1与∠2是( )
A.内错角
B.同位角
C.同旁内角
D.对顶角
【分析】根据同位角定义可得答案.
【解答】解:直线b、c被直线a所截,则∠1与∠2是同位角,
故选:B.
8.同一平面内两条直线的位置关系有( )
A.相交、垂直
B.相交、平行
C.垂直、平行
D.相交、垂直、平行
【分析】根据同一平面内的直线有相交与平行两种位置关系即可解答.
【解答】解:同一平面内的两直线只有相交与平行两种位置关系.
故选:B.
9.下列结论:①平面内3条直线两两相交,共有3个交点;②在平面内,若∠AOB=40°,∠AOC=∠BOC,则∠AOC的度数为20°;③若线段AB=3,BC=2,则线段AC的长为1或5;④若∠α+∠β=180°,且∠α<∠β,则∠α的余角为(∠β﹣∠α).其中正确结论的个数有( )
A.1个
B.2个
C.3个
D.4个
【分析】根据线段的和差,相交线的定义,角平分线的定义,余角和补角的定义进行判断找到正确的答案即可.
【解答】解:①平面内3条直线两两相交,有1个或3个交点;故错误;
②在平面内,若∠AOB=40°,∠AOC=∠BOC,则∠AOC的度数为20°或160°;故错误;
③若线段AB=3,BC=2,则线段AC的长为1或5;点C不一定在直线AB上,故错误;
④若∠α+∠β=180°,且∠α<∠β,则∠α的余角为(∠β﹣∠α),故正确.
故选:A.
10.观察图形,并阅读相关的文字:那么8条直线相交,最多可形成交点的个数是( )
A.21
B.28
C.36
D.45
【分析】解答此题的关键是观察图形找出规律,如果8条直线相交,那么每条直线最多可形成7个交点.然后即可得出答案.
【解答】解:观察图形可得:
n条直线相交最多可形成的交点个数为,
∴8条直线相交,最多可形成交点的个数为====28.
故选:B.
二.填空题(共10小题)
11.如图,直线AB,CD相交于点O,OA平分∠EOC.若∠AOE=36°,则∠DOE= 108 °.
【分析】根据角平分线的定义可得∠COE=2∠AOE,再根据补角的定义解答即可.
【解答】解:∠DOE=∠COD﹣∠COE
=180°﹣36°×2
=180°﹣72°
=108°.
故答案为:108.
12.如图直线AB,CD相交于O,直线FE⊥AB于O,∠BOD=75°,则∠COF的度数为 15 度.
【分析】利用图中角与角的关系即可求得,即∠COF=∠DOE=90°﹣∠BOD.
【解答】解:∵直线FE⊥AB于O,
∴∠BOE=90°,
∵∠DOE=∠BOE﹣∠BOD,∠BOD=75°,
∴∠DOE=15°,
∴∠COF=∠DOE=15°.
故答案为:15.
13.如图,∠1与∠2是直线 a 和
被直线 c 所截的一对 内错 角.
【分析】利用内错角定义进行解答即可.
【解答】解:∠1与∠2是直线a和b被直线c所截的一对内错角.
故答案为:a;b;c;内错.
14.三条直线相交,最多有 3 个交点.
【分析】三条直线相交,有三种情况,即:两条直线平行,被第三条直线所截,有两个交点;三条直线经过同一个点,有一个交点;三条直线两两相交且不经过同一点,有三个交点.故可得答案.
【解答】解:三条直线相交时,位置关系如图所示:
判断可知:最多有3个交点.
15.如图所示,在铁路旁边有一李庄,现要建一火车站,为了使李庄人乘火车最方便(即距离最近),请你在铁路旁选一点来建火车站(位置已选好),说明理由: 垂线段最短 .
【分析】根据从直线外一点到这条直线上各点所连的线段中,垂线段最短可知,要选垂线段.
【解答】解:为了使李庄人乘火车最方便(即距离最近),过李庄向铁路画垂线段,根据是垂线段最短.
故答案为:垂线段最短.
16.若平面上4条直线两两相交且无三线共点,则共有同旁内角 24 对.
【分析】一条直线与另3条直线相交(不交于一点),有3个交点.每2个交点决定一条线段,共有3条线段.4条直线两两相交且无三线共点,共有3×4=12条线段.每条线段两侧各有一对同旁内角,可知同旁内角的总对数.
【解答】解:∵平面上4条直线两两相交且无三线共点,
∴共有3×4=12条线段.
又∵每条线段两侧各有一对同旁内角,
∴共有同旁内角
12×2=24对.
故答案为:24.
17.平面内有四条不同的直线两两相交,若最多有m个交点,最少有n个交点,那么(﹣n)m= 1 .
【分析】根据每三条不交于同一点,可得m,根据都交于同一点,可得n,根据乘方的意义,可得答案.
【解答】解:每三条不交于同一点,得
m==6,
都交于同一点,得n=1,
(﹣1)6=1,
故答案为:1.
18.如图,在△ABC中,∠ACB=90°,CD⊥AD,垂足为点D,那么点B到直线CD的距离是线段 BD 的长.
【分析】根据点到直线的距离,即可解答.
【解答】解:∵CD⊥AD,垂足为点D,
∴点B到直线CD的距离是线段BD的长,
故答案为:BD.
19.平面上不重合的四条直线,可能产生交点的个数为 0,1,3,4,5,6 个.
【分析】从平行线的角度考虑,先考虑四条直线都平行,再考虑三条、两条直至都不平行,作出草图即可看出.
【解答】解:(1)当四条直线平行时,无交点;
(2)当三条平行,另一条与这三条不平行时,有三个交点;
(3)当两两直线平行时,有4个交点;
(4)当有两条直线平行,而另两条不平行时,有5个交点;
(5)当四条直线同交于一点时,只有一个交点;
(6)当四条直线两两相交,且不过同一点时,有6个交点;
(7)当有两条直线平行,而另两条不平行并且交点在平行线上时,有3个交点.
故答案为:0,1,3,4,5,6.
20.在一平面中,两条直线相交有一个交点;三条直线两两相交最多有3个交点;四条直线两两相交最多有6个交点……当相交直线的条数从2至n变化时,最多可有的交点数P与直线条数n之间的关系如下表:
直线条数n/条
2
3
4
5
6
7
8
…
最多交点个数p/个
1
3
6
10
…
…
…
…
则n与p的关系式为: p=n(n﹣1) .
【分析】根据题意,3条直线相交最多有3个交点,4条直线相交最多有6个交点,5条直线相交最多有10个交点.而3=1+2,6=1+2+3,10=1+2+3+4,故可猜想,n条直线相交,最多有1+2+3+…+(n﹣1)=n(n﹣1)个交点.
【解答】解:∵3条直线相交最多有3个交点,4条直线相交最多有6个交点.
而3=1+2,6=1+2+3,10=1+2+3+4,
∴可猜想,n条直线相交,最多有1+2+3+…+(n﹣1)=n(n﹣1)个交点.
即p=n(n﹣1),
故答案为:p=n(n﹣1).
三.解答题(共6小题)
21.如图,在直角三角形ABC中,∠C=90°.
(1)画出点C到AB的最短路径CD;
(2)请指出B到AC的距离是线段 BC 的长度.
【分析】根据点到直线的距离垂线段最短,即可得出答案.
【解答】解:(1)根据题意,如图所示,
(2)B到AC的距离是线段BC的长度,
故答案为:BC.
22.如图,两直线AB,CD相交于点O,OE平分∠BOD,且∠AOC:∠AOD=3:7
(1)求∠DOE的度数;
(2)若∠EOF是直角,求∠COF的度数.
【分析】(1)求出∠AOC=54°,∠AOD=126°,根据对顶角相等得出∠BOD=∠AOC=54°,根据角平分线定义求出即可;
(2)求出∠DOF=63°,代入∠AOF=∠AOD﹣∠DOF求出∠AOF,代入∠COF=∠AOC+∠AOF求出即可.
【解答】解:(1)
∵∠AOC:∠AOD=3:7,
∴∠AOC=54°,∠AOD=126°,
∴∠BOD=∠AOC=54°,
∵OE平分∠BOD,
∴∠DOE=∠BOD=×54°=27°;
(2)∵∠EOF是直角,∠DOE=27°,
∴∠DOF=90°﹣27°=63°,
∵∠AOD=126°,
∴∠AOF=∠AOD﹣∠DOF=126°﹣63°=63°,
∴∠COF=∠AOC+∠AOF=54°°+63°=117°.
23.如图,直线AB、CD交于O点,且∠BOC=80°,OE平分∠BOC,OF为OE的反向延长线.
(1)求∠2和∠3的度数;
(2)OF平分∠AOD吗?为什么?
【分析】(1)根据邻补角的定义,即可求得∠2的度数,根据角平分线的定义和平角的定义即可求得∠3的度数;
(2)根据OF分∠AOD的两部分角的度数即可说明.
【解答】解:(1)∵∠BOC+∠2=180°,∠BOC=80°,
∴∠2=180°﹣80°=100°;
∵OE是∠BOC的角平分线,
∴∠1=40°.
∵∠1+∠2+∠3=180°,
∴∠3=180°﹣∠1﹣∠2=180°﹣40°﹣100°=40°.
(2)平分
理由:∵∠2+∠3+∠AOF=180°,
∴∠AOF=180°﹣∠2﹣∠3=180°﹣100°﹣40°=40°.
∴∠AOF=∠3=40°,
∴OF平分∠AOD.
24.如图,点O是直线AB上一点,∠AOC=40°,OD平分∠AOC,∠COE=70°.
(1)请你说明DO⊥OE;
(2)OE平分∠BOC吗?为什么?
【分析】(1)根据角平分线的定义求得∠COD=20°,再根据垂线的定义证明;
(2)求得∠BOC的度数,根据角平分线的定义即可求得OE平分∠BOC.
【解答】解:(1)∵OD平分∠AOC,
∴∠DOC=∠AOC=20.
∵∠COE=70°,
∴∠DOE=90°,
∴DO⊥OE.
(2)OE平分∠BOC.
理由:∵∠AOC+∠COE+∠BOE=180°,
又∵∠AOC=40°,∠COE=70°,
∴∠BOE=70°,
∴∠BOE=∠COE,
∴OE平分∠BOC.
25.如图,点P,点Q分别代表两个村庄,直线l代表两个村庄中间的一条公路.根据居民出行的需要,计划在公路l上的某处设置一个公交站.
(1)若考虑到村庄P居住的老年人较多,计划建一个离村庄P最近的车站,请在公路l上画出车站的位置(用点M表示),依据是 直线外一点与直线上各点连接的所有线段中垂线段最短 ;
(2)若考虑到修路的费用问题,希望车站的位置到村庄P和村庄Q的距离之和最小,请在公路l上画出车站的位置(用点N表示),依据是 两点之间线段最短 .
【分析】(1)直接利用点到直线的距离的定义得出答案;
(2)利用线段的性质得出答案.
【解答】解:(1)如图,点M即为所示.依据是直线外一点与直线上各点连接的所有线段中垂线段最短
(2)如图,点N即为所示.依据是两点之间线段最短;
故答案为:直线外一点与直线上各点连接的所有线段中垂线段最短;两点之间线段最短.
26.平面内有不重合的4条直线,请指出这4条直线交点个数的所有情况,并画出相应的草图.
【分析】从平行线的角度考虑,先考虑四条直线都平行,再考虑三条、两条直至都不平行,作出草图即可看出.
【解答】解:(1)当四条直线平行时,无交点,
(2)当三条平行,另一条与这三条不平行时,有3个交点,
(3)当两两直线平行时,有4个交点,
(4)当有两条直线平行,而另两条不平行时,有5个交点,
(5)当四条直线同交于一点时,只有1个交点,
(6)当四条直线两两相交,且不过同一点时,有6个交点,
(7)当有两条直线平行,而另两条不平行并且交点在平行线上时,有3个交点,
(8)当三条直线交于一点,第四条直线与其它三条直线有三个交点时,共有4个交点,
故4条直线交点个数为:0或1或3或4或5或6.
相交线与平行线
一.选择题
1.三条直线相交,交点最多有( )
A.1个
B.2个
C.3个
D.4个
2.如图所示,∠2和∠1是对顶角的是( )
A.
B.
C.
D.
3.如图,OA⊥OB,OC⊥OD,若∠1=50°,则∠2的度数是( )
A.20°
B.40°
C.50°
D.60°
4.如图,三角形ABC中,∠C=90°,AC=3,AB=6,点P是边BC上的动点,则AP的长不可能是( )
A.2.5
B.3
C.4
D.5
5.如图,已知直角△ABC中,∠ACB=90°,CD⊥AB于点D,则表示点A到直线CD距离的是( )
A.线段CD的长度
B.线段AC的长度
C.线段AD的长度
D.线段BC的长度
6.如图,∠1和∠2不是同位角的是( )
A.
B.
C.
D.
7.如图,直线b、c被直线a所截,则∠1与∠2是( )
A.内错角
B.同位角
C.同旁内角
D.对顶角
8.同一平面内两条直线的位置关系有( )
A.相交、垂直
B.相交、平行
C.垂直、平行
D.相交、垂直、平行
9.下列结论:①平面内3条直线两两相交,共有3个交点;②在平面内,若∠AOB=40°,∠AOC=∠BOC,则∠AOC的度数为20°;③若线段AB=3,BC=2,则线段AC的长为1或5;④若∠α+∠β=180°,且∠α<∠β,则∠α的余角为(∠β﹣∠α).其中正确结论的个数有( )
A.1个
B.2个
C.3个
D.4个
10.观察图形,并阅读相关的文字:那么8条直线相交,最多可形成交点的个数是( )
A.21
B.28
C.36
D.45
二.填空题
11.如图,直线AB,CD相交于点O,OA平分∠EOC.若∠AOE=36°,则∠DOE=
°.
12.如图直线AB,CD相交于O,直线FE⊥AB于O,∠BOD=75°,则∠COF的度数为
度.
13.如图,∠1与∠2是直线
和
被直线
所截的一对
角.
14.三条直线相交,最多有
个交点.
15.如图所示,在铁路旁边有一李庄,现要建一火车站,为了使李庄人乘火车最方便(即距离最近),请你在铁路旁选一点来建火车站(位置已选好),说明理由:
.
16.若平面上4条直线两两相交且无三线共点,则共有同旁内角
对.
17.平面内有四条不同的直线两两相交,若最多有m个交点,最少有n个交点,那么(﹣n)m=
.
18.如图,在△ABC中,∠ACB=90°,CD⊥AD,垂足为点D,那么点B到直线CD的距离是线段
的长.
19.平面上不重合的四条直线,可能产生交点的个数为
个.
20.在一平面中,两条直线相交有一个交点;三条直线两两相交最多有3个交点;四条直线两两相交最多有6个交点……当相交直线的条数从2至n变化时,最多可有的交点数P与直线条数n之间的关系如下表:
直线条数n/条
2
3
4
5
6
7
8
…
最多交点个数p/个
1
3
6
10
…
…
…
…
则n与p的关系式为:
.
三.解答题
21.如图,在直角三角形ABC中,∠C=90°.
(1)画出点C到AB的最短路径CD;
(2)请指出B到AC的距离是线段
的长度.
22.如图,两直线AB,CD相交于点O,OE平分∠BOD,且∠AOC:∠AOD=3:7
(1)求∠DOE的度数;
(2)若∠EOF是直角,求∠COF的度数.
23.如图,直线AB、CD交于O点,且∠BOC=80°,OE平分∠BOC,OF为OE的反向延长线.
(1)求∠2和∠3的度数;
(2)OF平分∠AOD吗?为什么?
24.如图,点O是直线AB上一点,∠AOC=40°,OD平分∠AOC,∠COE=70°.
(1)请你说明DO⊥OE;
(2)OE平分∠BOC吗?为什么?
25.如图,点P,点Q分别代表两个村庄,直线l代表两个村庄中间的一条公路.根据居民出行的需要,计划在公路l上的某处设置一个公交站.
(1)若考虑到村庄P居住的老年人较多,计划建一个离村庄P最近的车站,请在公路l上画出车站的位置(用点M表示),依据是
;
(2)若考虑到修路的费用问题,希望车站的位置到村庄P和村庄Q的距离之和最小,请在公路l上画出车站的位置(用点N表示),依据是
.
26.平面内有不重合的4条直线,请指出这4条直线交点个数的所有情况,并画出相应的草图.
参考答案与试题解析
一.选择题(共10小题)
1.三条直线相交,交点最多有( )
A.1个
B.2个
C.3个
D.4个
【分析】根据题意画出图形可得答案.
【解答】解:如图:
,
交点最多3个,
故选:C.
2.如图所示,∠2和∠1是对顶角的是( )
A.
B.
C.
D.
【分析】根据对顶角的定义对各图形判断即可.
【解答】解:A.∠1和∠2不是对顶角,
B.∠1和∠2不是对顶角,
C.∠1和∠2是对顶角,
D.∠1和∠2不是对顶角.
3.如图,OA⊥OB,OC⊥OD,若∠1=50°,则∠2的度数是( )
A.20°
B.40°
C.50°
D.60°
【分析】先求出∠BOC,即可求出∠2.
【解答】解:∵OA⊥OB,OC⊥OD,∴∠AOB=∠COD=90°.
∠BOC=∠AOB﹣∠1=90°﹣50°=40°,
∠2=∠COD﹣∠BOC=90°﹣40°=50°.
故选:C.
4.如图,三角形ABC中,∠C=90°,AC=3,AB=6,点P是边BC上的动点,则AP的长不可能是( )
A.2.5
B.3
C.4
D.5
【分析】根据垂线段最短,可得答案.
【解答】解:由垂线段最短,得
AP≥AC=3,
故选:A.
5.如图,已知直角△ABC中,∠ACB=90°,CD⊥AB于点D,则表示点A到直线CD距离的是( )
A.线段CD的长度
B.线段AC的长度
C.线段AD的长度
D.线段BC的长度
【分析】根据点到直线的距离的概念:直线外一点到这条直线的垂线段的长度即为该点到这条直线的距离作答.
【解答】解:点A到CD的距离是线段AD的长度.
故选:C.
6.如图,∠1和∠2不是同位角的是( )
A.
B.
C.
D.
【分析】利用同位角的定义,直接分析得出即可.
【解答】解:A、∠1和∠2是同位角,故此选项不符合题意;
B、∠1和∠2是同位角,故此选项不符合题意;
C、∠1和∠2是同位角,故此选项不符合题意;
D、∠1和∠2不是同位角,故此选项符合题意;
故选:D.
7.如图,直线b、c被直线a所截,则∠1与∠2是( )
A.内错角
B.同位角
C.同旁内角
D.对顶角
【分析】根据同位角定义可得答案.
【解答】解:直线b、c被直线a所截,则∠1与∠2是同位角,
故选:B.
8.同一平面内两条直线的位置关系有( )
A.相交、垂直
B.相交、平行
C.垂直、平行
D.相交、垂直、平行
【分析】根据同一平面内的直线有相交与平行两种位置关系即可解答.
【解答】解:同一平面内的两直线只有相交与平行两种位置关系.
故选:B.
9.下列结论:①平面内3条直线两两相交,共有3个交点;②在平面内,若∠AOB=40°,∠AOC=∠BOC,则∠AOC的度数为20°;③若线段AB=3,BC=2,则线段AC的长为1或5;④若∠α+∠β=180°,且∠α<∠β,则∠α的余角为(∠β﹣∠α).其中正确结论的个数有( )
A.1个
B.2个
C.3个
D.4个
【分析】根据线段的和差,相交线的定义,角平分线的定义,余角和补角的定义进行判断找到正确的答案即可.
【解答】解:①平面内3条直线两两相交,有1个或3个交点;故错误;
②在平面内,若∠AOB=40°,∠AOC=∠BOC,则∠AOC的度数为20°或160°;故错误;
③若线段AB=3,BC=2,则线段AC的长为1或5;点C不一定在直线AB上,故错误;
④若∠α+∠β=180°,且∠α<∠β,则∠α的余角为(∠β﹣∠α),故正确.
故选:A.
10.观察图形,并阅读相关的文字:那么8条直线相交,最多可形成交点的个数是( )
A.21
B.28
C.36
D.45
【分析】解答此题的关键是观察图形找出规律,如果8条直线相交,那么每条直线最多可形成7个交点.然后即可得出答案.
【解答】解:观察图形可得:
n条直线相交最多可形成的交点个数为,
∴8条直线相交,最多可形成交点的个数为====28.
故选:B.
二.填空题(共10小题)
11.如图,直线AB,CD相交于点O,OA平分∠EOC.若∠AOE=36°,则∠DOE= 108 °.
【分析】根据角平分线的定义可得∠COE=2∠AOE,再根据补角的定义解答即可.
【解答】解:∠DOE=∠COD﹣∠COE
=180°﹣36°×2
=180°﹣72°
=108°.
故答案为:108.
12.如图直线AB,CD相交于O,直线FE⊥AB于O,∠BOD=75°,则∠COF的度数为 15 度.
【分析】利用图中角与角的关系即可求得,即∠COF=∠DOE=90°﹣∠BOD.
【解答】解:∵直线FE⊥AB于O,
∴∠BOE=90°,
∵∠DOE=∠BOE﹣∠BOD,∠BOD=75°,
∴∠DOE=15°,
∴∠COF=∠DOE=15°.
故答案为:15.
13.如图,∠1与∠2是直线 a 和
被直线 c 所截的一对 内错 角.
【分析】利用内错角定义进行解答即可.
【解答】解:∠1与∠2是直线a和b被直线c所截的一对内错角.
故答案为:a;b;c;内错.
14.三条直线相交,最多有 3 个交点.
【分析】三条直线相交,有三种情况,即:两条直线平行,被第三条直线所截,有两个交点;三条直线经过同一个点,有一个交点;三条直线两两相交且不经过同一点,有三个交点.故可得答案.
【解答】解:三条直线相交时,位置关系如图所示:
判断可知:最多有3个交点.
15.如图所示,在铁路旁边有一李庄,现要建一火车站,为了使李庄人乘火车最方便(即距离最近),请你在铁路旁选一点来建火车站(位置已选好),说明理由: 垂线段最短 .
【分析】根据从直线外一点到这条直线上各点所连的线段中,垂线段最短可知,要选垂线段.
【解答】解:为了使李庄人乘火车最方便(即距离最近),过李庄向铁路画垂线段,根据是垂线段最短.
故答案为:垂线段最短.
16.若平面上4条直线两两相交且无三线共点,则共有同旁内角 24 对.
【分析】一条直线与另3条直线相交(不交于一点),有3个交点.每2个交点决定一条线段,共有3条线段.4条直线两两相交且无三线共点,共有3×4=12条线段.每条线段两侧各有一对同旁内角,可知同旁内角的总对数.
【解答】解:∵平面上4条直线两两相交且无三线共点,
∴共有3×4=12条线段.
又∵每条线段两侧各有一对同旁内角,
∴共有同旁内角
12×2=24对.
故答案为:24.
17.平面内有四条不同的直线两两相交,若最多有m个交点,最少有n个交点,那么(﹣n)m= 1 .
【分析】根据每三条不交于同一点,可得m,根据都交于同一点,可得n,根据乘方的意义,可得答案.
【解答】解:每三条不交于同一点,得
m==6,
都交于同一点,得n=1,
(﹣1)6=1,
故答案为:1.
18.如图,在△ABC中,∠ACB=90°,CD⊥AD,垂足为点D,那么点B到直线CD的距离是线段 BD 的长.
【分析】根据点到直线的距离,即可解答.
【解答】解:∵CD⊥AD,垂足为点D,
∴点B到直线CD的距离是线段BD的长,
故答案为:BD.
19.平面上不重合的四条直线,可能产生交点的个数为 0,1,3,4,5,6 个.
【分析】从平行线的角度考虑,先考虑四条直线都平行,再考虑三条、两条直至都不平行,作出草图即可看出.
【解答】解:(1)当四条直线平行时,无交点;
(2)当三条平行,另一条与这三条不平行时,有三个交点;
(3)当两两直线平行时,有4个交点;
(4)当有两条直线平行,而另两条不平行时,有5个交点;
(5)当四条直线同交于一点时,只有一个交点;
(6)当四条直线两两相交,且不过同一点时,有6个交点;
(7)当有两条直线平行,而另两条不平行并且交点在平行线上时,有3个交点.
故答案为:0,1,3,4,5,6.
20.在一平面中,两条直线相交有一个交点;三条直线两两相交最多有3个交点;四条直线两两相交最多有6个交点……当相交直线的条数从2至n变化时,最多可有的交点数P与直线条数n之间的关系如下表:
直线条数n/条
2
3
4
5
6
7
8
…
最多交点个数p/个
1
3
6
10
…
…
…
…
则n与p的关系式为: p=n(n﹣1) .
【分析】根据题意,3条直线相交最多有3个交点,4条直线相交最多有6个交点,5条直线相交最多有10个交点.而3=1+2,6=1+2+3,10=1+2+3+4,故可猜想,n条直线相交,最多有1+2+3+…+(n﹣1)=n(n﹣1)个交点.
【解答】解:∵3条直线相交最多有3个交点,4条直线相交最多有6个交点.
而3=1+2,6=1+2+3,10=1+2+3+4,
∴可猜想,n条直线相交,最多有1+2+3+…+(n﹣1)=n(n﹣1)个交点.
即p=n(n﹣1),
故答案为:p=n(n﹣1).
三.解答题(共6小题)
21.如图,在直角三角形ABC中,∠C=90°.
(1)画出点C到AB的最短路径CD;
(2)请指出B到AC的距离是线段 BC 的长度.
【分析】根据点到直线的距离垂线段最短,即可得出答案.
【解答】解:(1)根据题意,如图所示,
(2)B到AC的距离是线段BC的长度,
故答案为:BC.
22.如图,两直线AB,CD相交于点O,OE平分∠BOD,且∠AOC:∠AOD=3:7
(1)求∠DOE的度数;
(2)若∠EOF是直角,求∠COF的度数.
【分析】(1)求出∠AOC=54°,∠AOD=126°,根据对顶角相等得出∠BOD=∠AOC=54°,根据角平分线定义求出即可;
(2)求出∠DOF=63°,代入∠AOF=∠AOD﹣∠DOF求出∠AOF,代入∠COF=∠AOC+∠AOF求出即可.
【解答】解:(1)
∵∠AOC:∠AOD=3:7,
∴∠AOC=54°,∠AOD=126°,
∴∠BOD=∠AOC=54°,
∵OE平分∠BOD,
∴∠DOE=∠BOD=×54°=27°;
(2)∵∠EOF是直角,∠DOE=27°,
∴∠DOF=90°﹣27°=63°,
∵∠AOD=126°,
∴∠AOF=∠AOD﹣∠DOF=126°﹣63°=63°,
∴∠COF=∠AOC+∠AOF=54°°+63°=117°.
23.如图,直线AB、CD交于O点,且∠BOC=80°,OE平分∠BOC,OF为OE的反向延长线.
(1)求∠2和∠3的度数;
(2)OF平分∠AOD吗?为什么?
【分析】(1)根据邻补角的定义,即可求得∠2的度数,根据角平分线的定义和平角的定义即可求得∠3的度数;
(2)根据OF分∠AOD的两部分角的度数即可说明.
【解答】解:(1)∵∠BOC+∠2=180°,∠BOC=80°,
∴∠2=180°﹣80°=100°;
∵OE是∠BOC的角平分线,
∴∠1=40°.
∵∠1+∠2+∠3=180°,
∴∠3=180°﹣∠1﹣∠2=180°﹣40°﹣100°=40°.
(2)平分
理由:∵∠2+∠3+∠AOF=180°,
∴∠AOF=180°﹣∠2﹣∠3=180°﹣100°﹣40°=40°.
∴∠AOF=∠3=40°,
∴OF平分∠AOD.
24.如图,点O是直线AB上一点,∠AOC=40°,OD平分∠AOC,∠COE=70°.
(1)请你说明DO⊥OE;
(2)OE平分∠BOC吗?为什么?
【分析】(1)根据角平分线的定义求得∠COD=20°,再根据垂线的定义证明;
(2)求得∠BOC的度数,根据角平分线的定义即可求得OE平分∠BOC.
【解答】解:(1)∵OD平分∠AOC,
∴∠DOC=∠AOC=20.
∵∠COE=70°,
∴∠DOE=90°,
∴DO⊥OE.
(2)OE平分∠BOC.
理由:∵∠AOC+∠COE+∠BOE=180°,
又∵∠AOC=40°,∠COE=70°,
∴∠BOE=70°,
∴∠BOE=∠COE,
∴OE平分∠BOC.
25.如图,点P,点Q分别代表两个村庄,直线l代表两个村庄中间的一条公路.根据居民出行的需要,计划在公路l上的某处设置一个公交站.
(1)若考虑到村庄P居住的老年人较多,计划建一个离村庄P最近的车站,请在公路l上画出车站的位置(用点M表示),依据是 直线外一点与直线上各点连接的所有线段中垂线段最短 ;
(2)若考虑到修路的费用问题,希望车站的位置到村庄P和村庄Q的距离之和最小,请在公路l上画出车站的位置(用点N表示),依据是 两点之间线段最短 .
【分析】(1)直接利用点到直线的距离的定义得出答案;
(2)利用线段的性质得出答案.
【解答】解:(1)如图,点M即为所示.依据是直线外一点与直线上各点连接的所有线段中垂线段最短
(2)如图,点N即为所示.依据是两点之间线段最短;
故答案为:直线外一点与直线上各点连接的所有线段中垂线段最短;两点之间线段最短.
26.平面内有不重合的4条直线,请指出这4条直线交点个数的所有情况,并画出相应的草图.
【分析】从平行线的角度考虑,先考虑四条直线都平行,再考虑三条、两条直至都不平行,作出草图即可看出.
【解答】解:(1)当四条直线平行时,无交点,
(2)当三条平行,另一条与这三条不平行时,有3个交点,
(3)当两两直线平行时,有4个交点,
(4)当有两条直线平行,而另两条不平行时,有5个交点,
(5)当四条直线同交于一点时,只有1个交点,
(6)当四条直线两两相交,且不过同一点时,有6个交点,
(7)当有两条直线平行,而另两条不平行并且交点在平行线上时,有3个交点,
(8)当三条直线交于一点,第四条直线与其它三条直线有三个交点时,共有4个交点,
故4条直线交点个数为:0或1或3或4或5或6.
