2021——2022学年冀教版八年级数学上册第十四章 实数单元测试题(word版含答案)
文档属性
| 名称 | 2021——2022学年冀教版八年级数学上册第十四章 实数单元测试题(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 101.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-30 06:32:50 | ||
图片预览



文档简介
第十四章 实数
一、选择题(本大题有12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.在下列各数:,0,,0.,,,3.131131113…(每两个3之间依次多一个1),1-中,无理数有
( )
A.
2个
B.
3个
C.
4个
D.
5个
2.下列说法中,正确的是
( )
A.-4的算术平方根是2
B.-是5的一个平方根
C.(-1)2的立方根是-1
D.的立方根是4
3.下列各组数中互为相反数的是
( )
A.-2与
B.|-|与
C.-2与(-)2
D.2与
4.下列有关平方根的叙述,正确的个数是
( )
①如果a存在平方根,那么a>0;
②如果a有两个不相等的平方根,那么a>0;
③如果a没有平方根,那么a<0;
④如果a>0,那么a的平方根也大于0.
A.1
B.2
C.3
D.4
5.在某次数学小测中,老师给出了5道判断题.如图1为张晓亮的答卷,每个小题判断正确得20分,他的得分应是
( )
图1
A.100分
B.80分
C.60分
D.40分
6.下列说法错误的是
( )
A.近似数16.8与16.80表示的意义不同
B.近似数0.2900精确到0.0001
C.3.14159精确到百分位的近似数是3.14
D.0.01249精确到0.001的近似数是0.0125
7.估计+2的值在
( )
A.2和3之间
B.3和4之间
C.4和5之间
D.5和6之间
8.若+|y+3|=0,则的值为
( )
A.
B.-
C.
D.-
9.若2a-4与3a-1是同一个数的平方根,则a的值为
( )
A.1
B.3
C.-1
D.1或-3
10.用计算器计算,,,,…,根据你发现的规律,判断P=与Q=(n为大于1的整数)的大小关系为
( )
A.PB.P=Q
C.P>Q
D.与n的取值有关
11.如果(0( )
A.3个
B.4个
C.5个
D.6个
12.如图2,正方形的周长为8个单位长度,在该正方形的4个顶点处分别标上0,2,4,6,先让正方形上表示数字6的点与数轴上表示-3的点重合,再将数轴按顺时针方向环绕在该正方形上,则数轴上表示99的点与正方形上表示数字 的点重合
( )?
图2
A.0
B.2
C.4
D.6
二、填空题(本大题有4个小题,共15分.13—15小题,每小题3分,16小题有两个空,每空3分)
13.0.125的立方根是 .?
14.比较大小: ?.
15.若某数的两个平方根分别是a+1与a-3,则这个数是 .?
16.我们用符号[x]表示一个不大于实数x的最大整数,如:[3.69]=3,[-0.56]=-1,则按这个规律,[]= ,[--1]= .?
三、解答题(本大题有6个小题,共49分.解答应写出文字说明、证明过程或演算步骤)
17.(6分)计算:
(1)++;
(2)++.
18.(8分)已知2a+4的立方根是2,3a+b-1的算术平方根是3,的整数部分是c,求3a-b+c的值.
19.(8分)如图3,将数轴上标有字母的各点与下列实数对应起来:-,π,0,,2,-.
(1)点A表示的数是 ,点B表示的数是 ,点O表示的数是 ,点C表示的数是 ,点D表示的数是 ,点E表示的数是 ;?
(2)将-,π,0,,2,-用“<”号连接起来.
图3
20.(8分)嘉嘉用两张同样大小的长方形硬纸片拼接成一个面积为900
cm2的正方形硬纸片,如图4所示,按要求完成下列各题.
(1)求长方形硬纸片的长和宽.
(2)嘉嘉想用该正方形硬纸片制作一个体积为512
cm3的正方体无盖笔筒,请你判断该硬纸片是否够用.若够用,求剩余的硬纸片的面积;若不够用,求缺少的硬纸片的面积.
图4
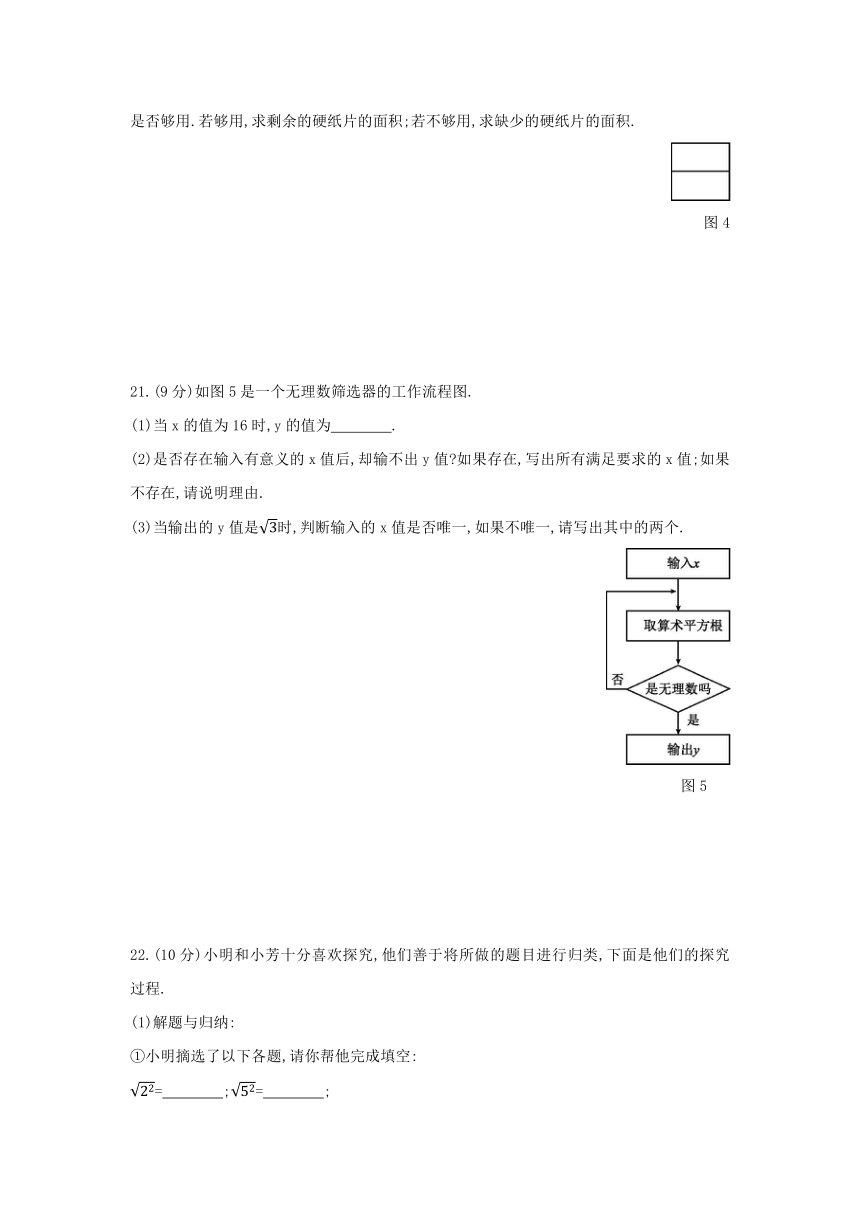
21.(9分)如图5是一个无理数筛选器的工作流程图.
(1)当x的值为16时,y的值为 .?
(2)是否存在输入有意义的x值后,却输不出y值?如果存在,写出所有满足要求的x值;如果不存在,请说明理由.
(3)当输出的y值是时,判断输入的x值是否唯一,如果不唯一,请写出其中的两个.
图5
22.(10分)小明和小芳十分喜欢探究,他们善于将所做的题目进行归类,下面是他们的探究过程.
(1)解题与归纳:
①小明摘选了以下各题,请你帮他完成填空:
= ;= ;?
= ;= ;?
= ;= .?
②归纳:对于任意数a,有= .?
③小芳摘选了以下各题,请你帮她完成填空:
= ;= ;= ;?
= ;= ;= .?
④归纳:对于任意非负数a,有= .?
(2)应用:
根据他们归纳得出的结论,解答问题:
数a,b在数轴上的对应点的位置如图6所示,化简:-+-.
图6
答案
1.C [解析]
,,3.131131113…(每两个3之间依次多一个1),1-是无理数,共4个.故选C.
2.B 3.C
4.B [解析]
①如果a存在平方根,那么a≥0,故①错误;
②如果a有两个不相等的平方根,那么a>0,故②正确;
③如果a没有平方根,那么a<0,故③正确;
④如果a>0,那么a的平方根不一定大于0,故④错误.
5.B [解析]
负数有立方根,故第1题判断正确;
是有理数,不是无理数,故第2题判断正确;
-=-,故第3题判断错误;
-1<2,故第4题判断正确;
数轴上有无理数,故第5题判断正确.
在张晓亮的答卷中判断正确的有4个,得80分,
故选B.
6.D
7.C [解析]
因为2<<3,
所以4<+2<5.
故选C.
8.C 9.D
10.C [解析]
利用计算器计算可知式子的结果分别约是1.732,1.414,1.291,1.225,…,发现结果逐渐减小,故P>Q.故选C.
11.B [解析]
因为=,
而(0所以5×5×2×3x一定可以写成平方的形式,
所以x可以是6,24,54,96,共4个.
故选B.
12.C [解析]
数轴上从表示-1的点到表示99的点共100个单位长度,正方形的周长为8个单位长度,100÷8=12……4,故数轴上表示99的点与正方形上表示数字4的点重合.
13.0.5 [解析]
∵0.53=0.125,∴0.125的立方根是0.5.
14.> [解析]
∵25<26<36,∴5<<6,∴1<-4<2,∴<<1,即>.
15.4 [解析]
因为一个数的两个平方根分别是a+1与a-3,
所以a+1+(a-3)=0,
解得a=1,
则a+1=2,
所以这个数是4.
故答案为4.
16.3 -4 [解析]
因为3<<4,所以[]=3;因为2<<3,所以-4<--1<-3,所以[--1]=-4.
17.解:(1)原式=+0+2=.
(2)原式=5+1-3=3.
18.解:因为2a+4的立方根是2,3a+b-1的算术平方根是3,
所以2a+4=8,3a+b-1=9,所以a=2,b=4.
因为c是的整数部分,所以c=3,
所以3a-b+c=3×2-4+3=5.
19.解:(1)- - 0 2 π
(2)-<-<0<<2<π.
20.解:(1)设长方形硬纸片的长为x
cm,宽为y
cm,则x=2y,且x2=900.
因为x>0,所以x=30,所以y=15.
即长方形硬纸片的长和宽分别为30
cm,15
cm.
(2)新制作的正方体无盖笔筒的棱长为=8(cm),正方体无盖笔筒的表面积为5×82=320(cm2).
因为320<900,
所以该硬纸片够用,剩余的硬纸片的面积为900-320=580(cm2).
21.解:(1) [解析]
当x=16时,=4,=2,是无理数,故y的值为.
(2)存在.当x=0,1时,始终输不出y值.因为0,1的算术平方根分别是0和1,一定是有理数.
(3)输入的x值不唯一.如x=3或x=9.
22.解:(1)①=2;
=5;=6;=0;=|-3|=3;=|-6|=6.
故答案为2,5,6,0,3,6.
②对于任意数a,有=|a|.
故答案为|a|.
③=4;=9;=25;=36;=49;
=0.
故答案为4,9,25,36,49,0.
④对于任意非负数a,有=a.
故答案为a.
(2)由数轴,得a<0,b>0,b>a,
所以a-b<0,b-a>0,
所以-+-
=|a|-|b|+|a-b|-(b-a)
=-a-b+b-a-b+a
=-a-b.
一、选择题(本大题有12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.在下列各数:,0,,0.,,,3.131131113…(每两个3之间依次多一个1),1-中,无理数有
( )
A.
2个
B.
3个
C.
4个
D.
5个
2.下列说法中,正确的是
( )
A.-4的算术平方根是2
B.-是5的一个平方根
C.(-1)2的立方根是-1
D.的立方根是4
3.下列各组数中互为相反数的是
( )
A.-2与
B.|-|与
C.-2与(-)2
D.2与
4.下列有关平方根的叙述,正确的个数是
( )
①如果a存在平方根,那么a>0;
②如果a有两个不相等的平方根,那么a>0;
③如果a没有平方根,那么a<0;
④如果a>0,那么a的平方根也大于0.
A.1
B.2
C.3
D.4
5.在某次数学小测中,老师给出了5道判断题.如图1为张晓亮的答卷,每个小题判断正确得20分,他的得分应是
( )
图1
A.100分
B.80分
C.60分
D.40分
6.下列说法错误的是
( )
A.近似数16.8与16.80表示的意义不同
B.近似数0.2900精确到0.0001
C.3.14159精确到百分位的近似数是3.14
D.0.01249精确到0.001的近似数是0.0125
7.估计+2的值在
( )
A.2和3之间
B.3和4之间
C.4和5之间
D.5和6之间
8.若+|y+3|=0,则的值为
( )
A.
B.-
C.
D.-
9.若2a-4与3a-1是同一个数的平方根,则a的值为
( )
A.1
B.3
C.-1
D.1或-3
10.用计算器计算,,,,…,根据你发现的规律,判断P=与Q=(n为大于1的整数)的大小关系为
( )
A.P
C.P>Q
D.与n的取值有关
11.如果(0
A.3个
B.4个
C.5个
D.6个
12.如图2,正方形的周长为8个单位长度,在该正方形的4个顶点处分别标上0,2,4,6,先让正方形上表示数字6的点与数轴上表示-3的点重合,再将数轴按顺时针方向环绕在该正方形上,则数轴上表示99的点与正方形上表示数字 的点重合
( )?
图2
A.0
B.2
C.4
D.6
二、填空题(本大题有4个小题,共15分.13—15小题,每小题3分,16小题有两个空,每空3分)
13.0.125的立方根是 .?
14.比较大小: ?.
15.若某数的两个平方根分别是a+1与a-3,则这个数是 .?
16.我们用符号[x]表示一个不大于实数x的最大整数,如:[3.69]=3,[-0.56]=-1,则按这个规律,[]= ,[--1]= .?
三、解答题(本大题有6个小题,共49分.解答应写出文字说明、证明过程或演算步骤)
17.(6分)计算:
(1)++;
(2)++.
18.(8分)已知2a+4的立方根是2,3a+b-1的算术平方根是3,的整数部分是c,求3a-b+c的值.
19.(8分)如图3,将数轴上标有字母的各点与下列实数对应起来:-,π,0,,2,-.
(1)点A表示的数是 ,点B表示的数是 ,点O表示的数是 ,点C表示的数是 ,点D表示的数是 ,点E表示的数是 ;?
(2)将-,π,0,,2,-用“<”号连接起来.
图3
20.(8分)嘉嘉用两张同样大小的长方形硬纸片拼接成一个面积为900
cm2的正方形硬纸片,如图4所示,按要求完成下列各题.
(1)求长方形硬纸片的长和宽.
(2)嘉嘉想用该正方形硬纸片制作一个体积为512
cm3的正方体无盖笔筒,请你判断该硬纸片是否够用.若够用,求剩余的硬纸片的面积;若不够用,求缺少的硬纸片的面积.
图4
21.(9分)如图5是一个无理数筛选器的工作流程图.
(1)当x的值为16时,y的值为 .?
(2)是否存在输入有意义的x值后,却输不出y值?如果存在,写出所有满足要求的x值;如果不存在,请说明理由.
(3)当输出的y值是时,判断输入的x值是否唯一,如果不唯一,请写出其中的两个.
图5
22.(10分)小明和小芳十分喜欢探究,他们善于将所做的题目进行归类,下面是他们的探究过程.
(1)解题与归纳:
①小明摘选了以下各题,请你帮他完成填空:
= ;= ;?
= ;= ;?
= ;= .?
②归纳:对于任意数a,有= .?
③小芳摘选了以下各题,请你帮她完成填空:
= ;= ;= ;?
= ;= ;= .?
④归纳:对于任意非负数a,有= .?
(2)应用:
根据他们归纳得出的结论,解答问题:
数a,b在数轴上的对应点的位置如图6所示,化简:-+-.
图6
答案
1.C [解析]
,,3.131131113…(每两个3之间依次多一个1),1-是无理数,共4个.故选C.
2.B 3.C
4.B [解析]
①如果a存在平方根,那么a≥0,故①错误;
②如果a有两个不相等的平方根,那么a>0,故②正确;
③如果a没有平方根,那么a<0,故③正确;
④如果a>0,那么a的平方根不一定大于0,故④错误.
5.B [解析]
负数有立方根,故第1题判断正确;
是有理数,不是无理数,故第2题判断正确;
-=-,故第3题判断错误;
-1<2,故第4题判断正确;
数轴上有无理数,故第5题判断正确.
在张晓亮的答卷中判断正确的有4个,得80分,
故选B.
6.D
7.C [解析]
因为2<<3,
所以4<+2<5.
故选C.
8.C 9.D
10.C [解析]
利用计算器计算可知式子的结果分别约是1.732,1.414,1.291,1.225,…,发现结果逐渐减小,故P>Q.故选C.
11.B [解析]
因为=,
而(0
所以x可以是6,24,54,96,共4个.
故选B.
12.C [解析]
数轴上从表示-1的点到表示99的点共100个单位长度,正方形的周长为8个单位长度,100÷8=12……4,故数轴上表示99的点与正方形上表示数字4的点重合.
13.0.5 [解析]
∵0.53=0.125,∴0.125的立方根是0.5.
14.> [解析]
∵25<26<36,∴5<<6,∴1<-4<2,∴<<1,即>.
15.4 [解析]
因为一个数的两个平方根分别是a+1与a-3,
所以a+1+(a-3)=0,
解得a=1,
则a+1=2,
所以这个数是4.
故答案为4.
16.3 -4 [解析]
因为3<<4,所以[]=3;因为2<<3,所以-4<--1<-3,所以[--1]=-4.
17.解:(1)原式=+0+2=.
(2)原式=5+1-3=3.
18.解:因为2a+4的立方根是2,3a+b-1的算术平方根是3,
所以2a+4=8,3a+b-1=9,所以a=2,b=4.
因为c是的整数部分,所以c=3,
所以3a-b+c=3×2-4+3=5.
19.解:(1)- - 0 2 π
(2)-<-<0<<2<π.
20.解:(1)设长方形硬纸片的长为x
cm,宽为y
cm,则x=2y,且x2=900.
因为x>0,所以x=30,所以y=15.
即长方形硬纸片的长和宽分别为30
cm,15
cm.
(2)新制作的正方体无盖笔筒的棱长为=8(cm),正方体无盖笔筒的表面积为5×82=320(cm2).
因为320<900,
所以该硬纸片够用,剩余的硬纸片的面积为900-320=580(cm2).
21.解:(1) [解析]
当x=16时,=4,=2,是无理数,故y的值为.
(2)存在.当x=0,1时,始终输不出y值.因为0,1的算术平方根分别是0和1,一定是有理数.
(3)输入的x值不唯一.如x=3或x=9.
22.解:(1)①=2;
=5;=6;=0;=|-3|=3;=|-6|=6.
故答案为2,5,6,0,3,6.
②对于任意数a,有=|a|.
故答案为|a|.
③=4;=9;=25;=36;=49;
=0.
故答案为4,9,25,36,49,0.
④对于任意非负数a,有=a.
故答案为a.
(2)由数轴,得a<0,b>0,b>a,
所以a-b<0,b-a>0,
所以-+-
=|a|-|b|+|a-b|-(b-a)
=-a-b+b-a-b+a
=-a-b.
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
