1.1.2程序框图与算法的基本逻辑结构-课件-2020-2021学年高二上学期数学人教A版必修3(66张PPT)
文档属性
| 名称 | 1.1.2程序框图与算法的基本逻辑结构-课件-2020-2021学年高二上学期数学人教A版必修3(66张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 13.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-29 15:05:19 | ||
图片预览







文档简介
§1.1.2程序框图与顺序结构(第一课时)
目录
学习目标
01
03
02
记住程序框图的符号及其功能
知道算法逻辑的顺序结构
能用顺序结构书写简单的算法
02
知道算法逻辑的顺序结构
复习导入
1.什么是算法?
2.算法的特征有哪些?
特征:有限性、确定性、顺序性、不唯一性、普遍性。
算法中的操作步骤都是顺序执行时比较容易理解.
缺点是如果算法中包含判断和转向,并且操作步骤较多时,就不那么直观清晰了.
复习导入
预学1:程序框图
程序框图又称流程图,是一种用程序框、流程线及文字说明来表示算法的图形.
想一想:在日常生活中,你见过类似的流程图吗?
【解析】各景点有路线图,许多单位的大厅有流程图,如医院看病的流程图等.
复习导入
复习导入
根据教材P6-P10,回答以下问题:
1.什么是程序框图?
2.基本的程序框有几种?它们表示的功能是什么?
3.程序框图中包含哪几种逻辑结构?
4.什么是顺序结构?
程序框图又称流程图,是一种用规定的图形、流程线及文字说明来准确、直观地表示算法的图形.
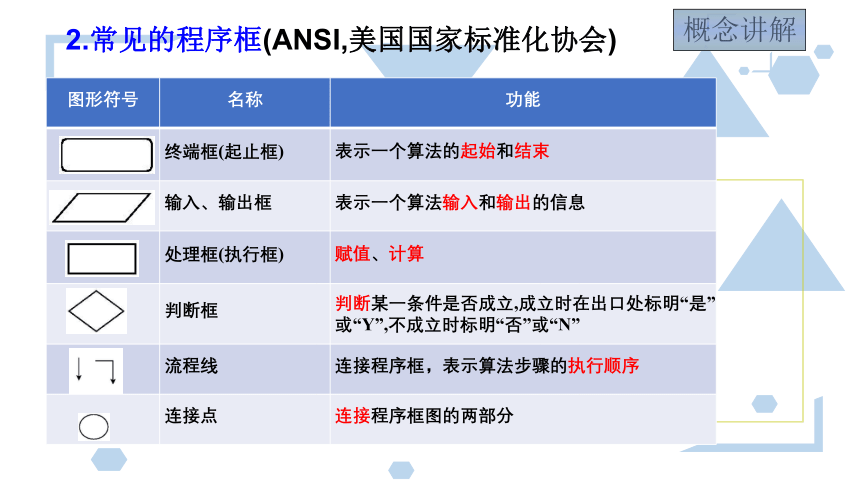
1.程序框图的概念
概念讲解
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}图形符号
名称
功能
终端框(起止框)
表示一个算法的起始和结束
输入、输出框
表示一个算法输入和输出的信息
处理框(执行框)
赋值、计算
判断框
判断某一条件是否成立,成立时在出口处标明“是”或“Y”,不成立时标明“否”或“N”
流程线
连接程序框,表示算法步骤的执行顺序
连接点
连接程序框图的两部分
概念讲解
2.常见的程序框(ANSI,美国国家标准化协会)
画程序框图注意的问题:
(1)使用标准的框图符号;
(2)框图一般按从上到下、从左到右的方向画;
(3)各程序框用流程线连接,表示算法步骤执行的先后顺序;
(4)完整的程序框图必须以 作为开始,以 作为结束;
(5)除判断框外,其他程序框图符号只有一个入口和一个出口。判断框是唯一具有两个出口的程序框;
(6)一种判断框是“是”与“否”两分支的判断,而且有且仅有两个结果;另一种是多分支判断,有几种不同的结果;
(7)一个框图可以没有输入,但必须有输出。
开始
结束
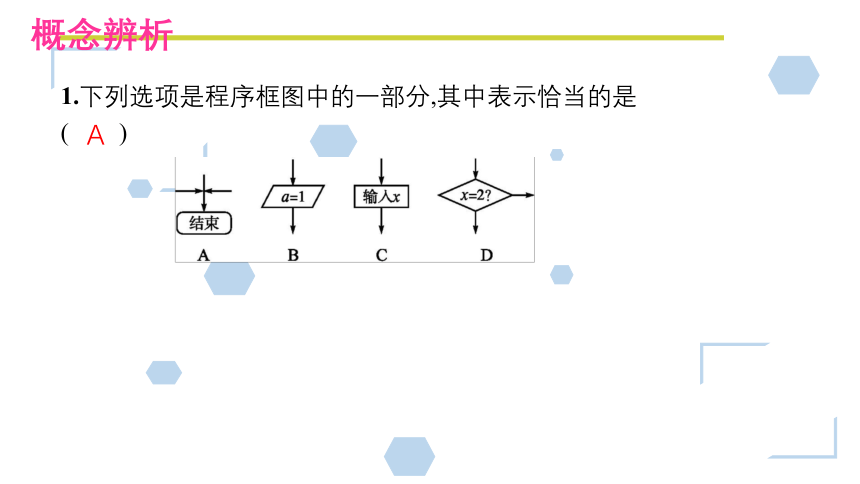
概念辨析
1.下列选项是程序框图中的一部分,其中表示恰当的是
( )
概念辨析
A
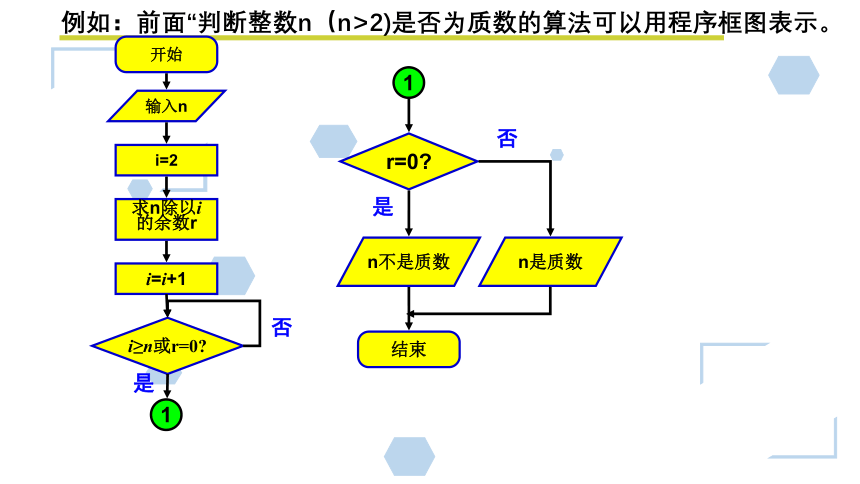
开始
输入n
i=2
i=i+1
i≥n或r=0?
n不是质数
结束
r=0?
1
否
是
求n除以i
的余数r
1
n是质数
是
否
例如:前面“判断整数n(n>2)是否为质数的算法可以用程序框图表示。
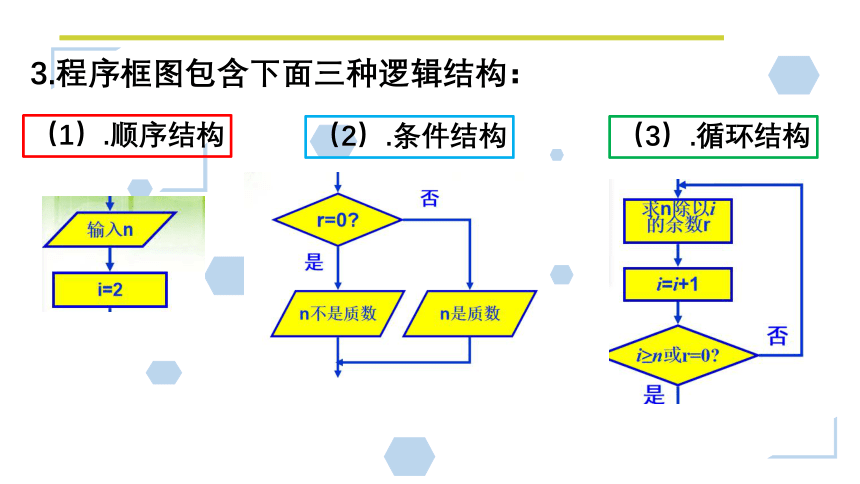
3.程序框图包含下面三种逻辑结构:
(1).顺序结构
(2).条件结构
(3).循环结构
算法的表示方法:
1. 用自然语言表示
2. 用程序框图表示
1). 用自然语言表示
优点是使用日常用语, 通俗易懂
缺点是文字冗长, 容易出现歧义
2). 用程序框图表示:
用图框表示各种操作
优点是直观形象, 易于理解
一般地,一个算法的程序框图可以分为以下几个步骤:
第一步:用自然语言表述算法步骤;
第二步:确定每一个算法步骤的逻辑结构;并用相应的程序框图表示。
第三步:将所有的步骤程序框图用流程线连接起来,加上终止框。
二、顺序结构及框图表示
1.顺序结构:按照步骤依次执行的一个算法,称为具有“顺序结构”的算法,或者称为算法的顺序结构.注:任何算法都离不开的基本结构。
2.顺序结构的流程图
语句A
语句B
顺序结构是最简单的结构:是从自上而下顺序而下的顺序进行的。
3.画顺序结构程序框图时注意事项
(1)在程序框图中,开始框和结束框不可少;
(2)在算法过程中,第一步输入语句是必不可少的;
(3)顺序结构在程序框图中的体现就是用流程线将程序框自上而下地连接起来,按顺序执行算法步骤.
题型一 把自然语言描述的算法翻译成程序框图
例1 已知一个算法如下:
第一步,输入x.
第二步,计算y=2x+3.
第三步,计算d= .
第四步,输出d.
把上述算法用程序框图表示.
跟踪训练1 算法如下,画出程序框图.
第一步,输入a,b,c的值-1,-2,3.
第二步,计算max=4????????-????24????.
第三步,输出max.
?
解 程序框图:
例2 已知一个三角形三边的边长分别为a,b,c,利用海伦-秦九韶公式,设计一个计算三角形面积的算法,并画出程序框图.
第一步:输入三角形
三边的边长a,b,c
第二步:计算
第三步:计算
第四步:输出S
算法分析:
程序框图:
开始
结束
输出s
输入a,b,c
题型二 画程序框图
1.已知球的半径为R,设计一个算法,求其表面积和体积.
算法分析:
第一步,输入球的半径R.
第二步,计算S=4πR2.
第三步,计算V= πR3.
第四步,输出S,V.
跟踪训练
程序框图:
1.已知球的半径为R,设计一个算法,求其表面积和体积.
跟踪训练
1.执行如图所示的程序框图,运行结果是( )
A.8 B.4 C.2 D.3
B
题型三 读懂程序框图
开始
c=7
结束
输出s
a=5
b=6
2.执行下面程序框图运行的结果是 .
跟踪训练
3.已知如图所示的程序框图,若输入x=32,则输出y的值为 .?
5
跟踪训练
4.如图,若输出的结果是2,则输入的m= .?
100
跟踪训练
5.如图所示的程序框图,
若输入的数n是5,则输出的y= ;
若输出的数是30,则输入的n= .
开始
结束
输入正整数n
输出y
y=x2+5
x=2n-1
86
3
跟踪训练
6.如图所示的程序框图,已知a1=3,输出的结果是7,则a2的值是( )
A.9 B.10 C.11 D.12
开始
结束
输出b
b=a1+a2
输入a1,a2
C
跟踪训练
7.下图的程序框图,最终输出的y1=3,y2=-2,5a+b=?
开始
结束
输出y1,y2
x=2
y1=ax+b
x=-3
y2=ax+b
跟踪训练
课堂小结:
布置作业:
1.本子上:△ABC的底边a为4, 底边上的高h为2,
求△ABC的面积S,试设计该问题的算法和程序框图。
2.小本65页
3.预习:条件结构(P10-P11)。
§1.1.2条件结构(第二课时)
目录
学习目标
01
03
02
掌握条件结构的两种形式及特征
知道算法逻辑的条件结构
能用条件结构书写简单的算法
02
复习导入
1.程序框图的概念?
1.程序框图又称流程图,是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形.
复习导入
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}图形符号
名称
功能
终端框(起止框)
表示一个算法的起始和结束
输入、输出框
表示一个算法输入和输出的信息
处理框(执行框)
赋值、计算
判断框
判断某一条件是否成立,成立时在出口处标明“是”或“Y”,不成立时标明“否”或“N”
流程线
连接程序框,表示算法步骤的执行顺序
连接点
连接程序框图的两部分
2.常见的程序框有哪些?
复习导入
3.什么叫顺序结构?
依次
无判断
无返回
复习导入
根据教材P10-P11,回答以下问题:
1.什么是条件结构?
2.条件结构有几种形式?
1.条件结构
概念讲解
在一个算法中,经常会遇到一些条件的判断,算法的流程根据条件是否成立有不同的流向.
基本形式1:符合条件就执行A,否则执行B
基本形式2:符合条件就执行A,否则执行条件结构后的步骤。
满足条件?
步骤A
步骤B
是
否
步骤A
满足条件?
是
否
二选一
选不选
例题分析
例3.任意给定3个正实数,设计一个算法,判断以这3个正实数为三条边边长的三角形是否存在,并画出这个算法的程序框图.
算 法
程序框图
开始
输入
是否同时成立?
存在这样的三角形
结束
不存在这样的三角形
第一步:输入 的值
第二步:判断 ,
, 是否同
时成立.若是,则存在这
样的三角形;否则,不
存在这样的三角形.
否
是
例题分析
例4.设计一个求解一元二次方程 的算法,并画出程序框图表示.
有两个不相等的实数根
有两个相等的实数根
没有实数根
算 法
第一步:输入三个系数
第二步:计算
第四步:判断
是否成立.若是,则输出
否则,计算
并输出
第三步:判断
是否成立.若是,则计算
否则,输出“方程没有实数根”,结束算法.
程序框图(1)
例题分析
开始
输入
输出
结束
输出“方程无实数根”
输出
是
是
否
否
程序框图(2)
跟踪训练
1.设计一个算法计算分段函数 的函数值,并画出程序框图。
第一步、输入x
第二步、判断“x<0”是否成立,若
是,则输出y=0,否则执行第三步;
第三步、判断“x<1”是否成立,若
是,则输出y=1,否则输出y=x。
程序框图:
算法步骤:
跟踪训练
输入x
开始
x>3?
y=1.2x+1.4
y=5
输出y
结束
否
是
P20 习题A组第3题
算法步骤:
第一步,输入人数x,设收取的
卫生费为y元.
第二步,判断x与3的大小,若x>3,则
费用为y= 5+(x-3)×1.2=1.2x+1.4;
若x≤3,则费用为y=5.
第三步,输出y.
程序框图:
跟踪训练
开始
输入a1,b1,c1, a2 。b2, c2
输出“x= ”; ,“y= ”;
a1b2-a2b1≠0?
x=(c2b1 -c1b2)/(a1b2 -a2b1)
y=(c2b1 -c1b2)/(a1b2 -a2b1)
结束
否
是
输出“输入数据不合题意”
P.20 习题1.1B组第1题
算法步骤:
第一步,输入a1,b1,c1,a2,b2,c2.
第二步,计算
x=(c2b1 -c1b2)/(a1b2 -a2b1)
y=(c2b1 -c1b2)/(a1b2 -a2b1)
第三步,输出x,y
程序框图:
课堂小结:
2.条件结构:条件结构是指在算法中通过对条件的判断,根据条件是否成立而选择不同流向的算法结构.
1.程序框图和顺序结构
布置作业:
1.大本P6-P7题型一和题型二。
2.小本67页【基础达标练】
3.预习:循环结构(P12-P19)。
§1.1.3循环结构(第三课时)
目录
学习目标
01
03
02
掌握循环结构的两种形式
(当型和直到型)
理解算法逻辑的循环结构
能用循环结构书写简单的算法
02
复习导入
1.什么叫顺序结构?
依次
无判断
无返回
复习导入
1.条件结构的两种形式?
满足条件?
步骤A
步骤B
是
否
步骤A
满足条件?
是
否
复习导入
1.什么是循环结构?
2.循环结构有几种形式?
概念讲解
循环结构分为当型循环结构和直到型循环结构
差异:循环终止条件不同,检验条件是否成立的先后次序也不同.
当型循环结构:先判断后执行循环体.
直到型循环结构:先执行循环体后判断条件是否成立.
循环体
满足条件?
否
是
直到型循环结构
当型循环结构
循环体
满足条件?
是
否
(3)循环结构
概念讲解
(1)确定循环结构的循环变量和初始条件;
(2)确定算法中需要反复执行的部分,即循环体;
(3)确定循环的终止条件.
循环结构一定包含条件结构,用以控制循环过程,避免出现“死循环”.判断框内写上条件,两个出口分别对应终止条件成立与否,其中一个指向循环体,经过循环体回到判断框的入口处.
循环结构的设计步骤
循环结构的三要素
循环变量,循环体、循环的终止条件.
概念讲解
?判断
循环体
满足条件?
是
否
直到型
满足条件?
循环体
否
是
当型
概念讲解
区别:循环结构具有重复性;条件结构具有选择性,不重复性。
1.条件结构和循环结构有什么区别和联系?
联系:循环结构中一定包含条件结构,用于确定何时终止执行循环体;条件结构中不含循环结构.
例题分析
第四步,判断“i>100”是否成立.
若是,则输出S,结束算法;
否则,返回第二步.
第一步,令i=1,S=0.
第二步,计算S+i,仍用S表示.
第三步,计算i+1,仍用i表示.
思考1:计算1+2+3+…+100的值的算法,并画 出程序框图。
算法分析:
知识探究(一):循环结构的程序框图
第一步,令i=1,S=0.
第二步,计算S+i,仍用S表示.
第三步,计算i+1,仍用i表示.
例题分析
思考2:用直到型循环结构,上述算法的程序框图如何表示?
开始
i=1
i>100?
是
输出S
结束
S=0
i=i+1
S=S+i
否
例题分析
思考3:用当型循环结构,上述算法的程序框图如何表示?
开始
i=1
结束
输出S
否
是
S=0
S=S+i
i≤100?
i=i+1
第二步,判断i≤100是否成立.
若是,则执行第三步;
否则,输出S,结束算法.
第一步,令i=1,S=0.
第三步,计算S+i,仍用S表示.
第四步,计算i+1,仍用i表示,
返回第三步.
例题分析
思考4:观察两个程序框图,直到型循环结构与当型循环结构如何转化?
开始
i=1
i>100?
是
输出S
结束
S=0
i=i+1
S=S+i
否
开始
i=1
结束
输出S
否
是
S=0
i≤100?
i=i+1
S=S+i
初始值
循环体
终止条件
例题分析
变式1:右边的程序框图,
输出S=———?
开始
i=1
i>3?
是
输出S
结束
S=0
i=i+1
S=S+i2
否
14
例题分析
题型二:程序框图的补充
1、求 的值。设计的算法框图如右,应该在空格位置填入什么条件?
分析:空格位置判断条件,应该考虑循环的终止条件是什么?
应该填入:i>10
例题分析
结束
输出S
i=0;S=0
开始
S=S+i
i=i+1
i>10?
否
是
2.如图所示的程序框图运行后,输出的结果为
55
i=0, s=0
i=1, s=0+1
i=2, s=0+1+2
i=3, s=0+1+2+3
i=4, s=0+1+2+3+4
i=5, s=0+1+2+3+4+5
i=6, s=0+1+2+3+4+5+6
i=7, s=0+1+2+3+4+5+6+7
i=8, s=0+1+2+3+4+5+6+7+8
i=9, s=0+1+2+3+4+5+6+7+8+9
i=10,s=0+1+2+3+4+5+6+7+8+9+10
i=11,s=....
例题分析
跟踪训练
3.设计一算法,求积:
1×2×3×…×100,画出流程图.
结束
输出S
i=1,S=1
S=S*i
i = i + 1
i>100?
开始
第四步,判断“i>100”是否成立.
若是,则输出S,结束算法;
否则,返回第二步.
算法分析:
第一步,令i=1,S=1.
第二步,计算S*i,仍用S表示.
第三步,计算i+1,仍用i表示.
否
是
跟踪训练
解:算法步骤:
第一步,令i=1,s=0.
第二步,判断“i≤100”若成立,则执行第三步,否则,输出s.
第三步,计算s=s+i2
第四步,计算i=i+1,返回第二步.
开始
i=1
S=0
i=i+1
S=S+i2
i≤100?
输出S
结束
否
是
当型循环结构
2、P.20习题A组第2题
课堂小结:
3.设计一个算法的程序框图的基本思路:
第二步,确定每个算法步骤所包含的逻辑结构,并用相应的程序框图表示.
第一步,用自然语言表述算法步骤.
第三步,将所有步骤的程序框图用流程线连接起来,并加上两个终端框.
首先确定循环体,再根据循环体第一步确定初值,
最后一步确定循环终止条件。
1.循环结构三要素:
循环变量赋初值、循环体、循环终止条件
2.循环三要素确定过程:
课堂小结:
1、循环结构的特点
2、循环结构的框图表示
3、循环结构该注意的问题
避免死循环的出现,设置好进入(结束)循环体的条件。
当型和直到型
重复同一个处理过程
布置作业:
1.大本P8小试身手。
2.小本69页【基础达标练】
3.预习:循环结构(P12-P19)。
谢 谢 欣 赏!
目录
学习目标
01
03
02
记住程序框图的符号及其功能
知道算法逻辑的顺序结构
能用顺序结构书写简单的算法
02
知道算法逻辑的顺序结构
复习导入
1.什么是算法?
2.算法的特征有哪些?
特征:有限性、确定性、顺序性、不唯一性、普遍性。
算法中的操作步骤都是顺序执行时比较容易理解.
缺点是如果算法中包含判断和转向,并且操作步骤较多时,就不那么直观清晰了.
复习导入
预学1:程序框图
程序框图又称流程图,是一种用程序框、流程线及文字说明来表示算法的图形.
想一想:在日常生活中,你见过类似的流程图吗?
【解析】各景点有路线图,许多单位的大厅有流程图,如医院看病的流程图等.
复习导入
复习导入
根据教材P6-P10,回答以下问题:
1.什么是程序框图?
2.基本的程序框有几种?它们表示的功能是什么?
3.程序框图中包含哪几种逻辑结构?
4.什么是顺序结构?
程序框图又称流程图,是一种用规定的图形、流程线及文字说明来准确、直观地表示算法的图形.
1.程序框图的概念
概念讲解
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}图形符号
名称
功能
终端框(起止框)
表示一个算法的起始和结束
输入、输出框
表示一个算法输入和输出的信息
处理框(执行框)
赋值、计算
判断框
判断某一条件是否成立,成立时在出口处标明“是”或“Y”,不成立时标明“否”或“N”
流程线
连接程序框,表示算法步骤的执行顺序
连接点
连接程序框图的两部分
概念讲解
2.常见的程序框(ANSI,美国国家标准化协会)
画程序框图注意的问题:
(1)使用标准的框图符号;
(2)框图一般按从上到下、从左到右的方向画;
(3)各程序框用流程线连接,表示算法步骤执行的先后顺序;
(4)完整的程序框图必须以 作为开始,以 作为结束;
(5)除判断框外,其他程序框图符号只有一个入口和一个出口。判断框是唯一具有两个出口的程序框;
(6)一种判断框是“是”与“否”两分支的判断,而且有且仅有两个结果;另一种是多分支判断,有几种不同的结果;
(7)一个框图可以没有输入,但必须有输出。
开始
结束
概念辨析
1.下列选项是程序框图中的一部分,其中表示恰当的是
( )
概念辨析
A
开始
输入n
i=2
i=i+1
i≥n或r=0?
n不是质数
结束
r=0?
1
否
是
求n除以i
的余数r
1
n是质数
是
否
例如:前面“判断整数n(n>2)是否为质数的算法可以用程序框图表示。
3.程序框图包含下面三种逻辑结构:
(1).顺序结构
(2).条件结构
(3).循环结构
算法的表示方法:
1. 用自然语言表示
2. 用程序框图表示
1). 用自然语言表示
优点是使用日常用语, 通俗易懂
缺点是文字冗长, 容易出现歧义
2). 用程序框图表示:
用图框表示各种操作
优点是直观形象, 易于理解
一般地,一个算法的程序框图可以分为以下几个步骤:
第一步:用自然语言表述算法步骤;
第二步:确定每一个算法步骤的逻辑结构;并用相应的程序框图表示。
第三步:将所有的步骤程序框图用流程线连接起来,加上终止框。
二、顺序结构及框图表示
1.顺序结构:按照步骤依次执行的一个算法,称为具有“顺序结构”的算法,或者称为算法的顺序结构.注:任何算法都离不开的基本结构。
2.顺序结构的流程图
语句A
语句B
顺序结构是最简单的结构:是从自上而下顺序而下的顺序进行的。
3.画顺序结构程序框图时注意事项
(1)在程序框图中,开始框和结束框不可少;
(2)在算法过程中,第一步输入语句是必不可少的;
(3)顺序结构在程序框图中的体现就是用流程线将程序框自上而下地连接起来,按顺序执行算法步骤.
题型一 把自然语言描述的算法翻译成程序框图
例1 已知一个算法如下:
第一步,输入x.
第二步,计算y=2x+3.
第三步,计算d= .
第四步,输出d.
把上述算法用程序框图表示.
跟踪训练1 算法如下,画出程序框图.
第一步,输入a,b,c的值-1,-2,3.
第二步,计算max=4????????-????24????.
第三步,输出max.
?
解 程序框图:
例2 已知一个三角形三边的边长分别为a,b,c,利用海伦-秦九韶公式,设计一个计算三角形面积的算法,并画出程序框图.
第一步:输入三角形
三边的边长a,b,c
第二步:计算
第三步:计算
第四步:输出S
算法分析:
程序框图:
开始
结束
输出s
输入a,b,c
题型二 画程序框图
1.已知球的半径为R,设计一个算法,求其表面积和体积.
算法分析:
第一步,输入球的半径R.
第二步,计算S=4πR2.
第三步,计算V= πR3.
第四步,输出S,V.
跟踪训练
程序框图:
1.已知球的半径为R,设计一个算法,求其表面积和体积.
跟踪训练
1.执行如图所示的程序框图,运行结果是( )
A.8 B.4 C.2 D.3
B
题型三 读懂程序框图
开始
c=7
结束
输出s
a=5
b=6
2.执行下面程序框图运行的结果是 .
跟踪训练
3.已知如图所示的程序框图,若输入x=32,则输出y的值为 .?
5
跟踪训练
4.如图,若输出的结果是2,则输入的m= .?
100
跟踪训练
5.如图所示的程序框图,
若输入的数n是5,则输出的y= ;
若输出的数是30,则输入的n= .
开始
结束
输入正整数n
输出y
y=x2+5
x=2n-1
86
3
跟踪训练
6.如图所示的程序框图,已知a1=3,输出的结果是7,则a2的值是( )
A.9 B.10 C.11 D.12
开始
结束
输出b
b=a1+a2
输入a1,a2
C
跟踪训练
7.下图的程序框图,最终输出的y1=3,y2=-2,5a+b=?
开始
结束
输出y1,y2
x=2
y1=ax+b
x=-3
y2=ax+b
跟踪训练
课堂小结:
布置作业:
1.本子上:△ABC的底边a为4, 底边上的高h为2,
求△ABC的面积S,试设计该问题的算法和程序框图。
2.小本65页
3.预习:条件结构(P10-P11)。
§1.1.2条件结构(第二课时)
目录
学习目标
01
03
02
掌握条件结构的两种形式及特征
知道算法逻辑的条件结构
能用条件结构书写简单的算法
02
复习导入
1.程序框图的概念?
1.程序框图又称流程图,是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形.
复习导入
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}图形符号
名称
功能
终端框(起止框)
表示一个算法的起始和结束
输入、输出框
表示一个算法输入和输出的信息
处理框(执行框)
赋值、计算
判断框
判断某一条件是否成立,成立时在出口处标明“是”或“Y”,不成立时标明“否”或“N”
流程线
连接程序框,表示算法步骤的执行顺序
连接点
连接程序框图的两部分
2.常见的程序框有哪些?
复习导入
3.什么叫顺序结构?
依次
无判断
无返回
复习导入
根据教材P10-P11,回答以下问题:
1.什么是条件结构?
2.条件结构有几种形式?
1.条件结构
概念讲解
在一个算法中,经常会遇到一些条件的判断,算法的流程根据条件是否成立有不同的流向.
基本形式1:符合条件就执行A,否则执行B
基本形式2:符合条件就执行A,否则执行条件结构后的步骤。
满足条件?
步骤A
步骤B
是
否
步骤A
满足条件?
是
否
二选一
选不选
例题分析
例3.任意给定3个正实数,设计一个算法,判断以这3个正实数为三条边边长的三角形是否存在,并画出这个算法的程序框图.
算 法
程序框图
开始
输入
是否同时成立?
存在这样的三角形
结束
不存在这样的三角形
第一步:输入 的值
第二步:判断 ,
, 是否同
时成立.若是,则存在这
样的三角形;否则,不
存在这样的三角形.
否
是
例题分析
例4.设计一个求解一元二次方程 的算法,并画出程序框图表示.
有两个不相等的实数根
有两个相等的实数根
没有实数根
算 法
第一步:输入三个系数
第二步:计算
第四步:判断
是否成立.若是,则输出
否则,计算
并输出
第三步:判断
是否成立.若是,则计算
否则,输出“方程没有实数根”,结束算法.
程序框图(1)
例题分析
开始
输入
输出
结束
输出“方程无实数根”
输出
是
是
否
否
程序框图(2)
跟踪训练
1.设计一个算法计算分段函数 的函数值,并画出程序框图。
第一步、输入x
第二步、判断“x<0”是否成立,若
是,则输出y=0,否则执行第三步;
第三步、判断“x<1”是否成立,若
是,则输出y=1,否则输出y=x。
程序框图:
算法步骤:
跟踪训练
输入x
开始
x>3?
y=1.2x+1.4
y=5
输出y
结束
否
是
P20 习题A组第3题
算法步骤:
第一步,输入人数x,设收取的
卫生费为y元.
第二步,判断x与3的大小,若x>3,则
费用为y= 5+(x-3)×1.2=1.2x+1.4;
若x≤3,则费用为y=5.
第三步,输出y.
程序框图:
跟踪训练
开始
输入a1,b1,c1, a2 。b2, c2
输出“x= ”; ,“y= ”;
a1b2-a2b1≠0?
x=(c2b1 -c1b2)/(a1b2 -a2b1)
y=(c2b1 -c1b2)/(a1b2 -a2b1)
结束
否
是
输出“输入数据不合题意”
P.20 习题1.1B组第1题
算法步骤:
第一步,输入a1,b1,c1,a2,b2,c2.
第二步,计算
x=(c2b1 -c1b2)/(a1b2 -a2b1)
y=(c2b1 -c1b2)/(a1b2 -a2b1)
第三步,输出x,y
程序框图:
课堂小结:
2.条件结构:条件结构是指在算法中通过对条件的判断,根据条件是否成立而选择不同流向的算法结构.
1.程序框图和顺序结构
布置作业:
1.大本P6-P7题型一和题型二。
2.小本67页【基础达标练】
3.预习:循环结构(P12-P19)。
§1.1.3循环结构(第三课时)
目录
学习目标
01
03
02
掌握循环结构的两种形式
(当型和直到型)
理解算法逻辑的循环结构
能用循环结构书写简单的算法
02
复习导入
1.什么叫顺序结构?
依次
无判断
无返回
复习导入
1.条件结构的两种形式?
满足条件?
步骤A
步骤B
是
否
步骤A
满足条件?
是
否
复习导入
1.什么是循环结构?
2.循环结构有几种形式?
概念讲解
循环结构分为当型循环结构和直到型循环结构
差异:循环终止条件不同,检验条件是否成立的先后次序也不同.
当型循环结构:先判断后执行循环体.
直到型循环结构:先执行循环体后判断条件是否成立.
循环体
满足条件?
否
是
直到型循环结构
当型循环结构
循环体
满足条件?
是
否
(3)循环结构
概念讲解
(1)确定循环结构的循环变量和初始条件;
(2)确定算法中需要反复执行的部分,即循环体;
(3)确定循环的终止条件.
循环结构一定包含条件结构,用以控制循环过程,避免出现“死循环”.判断框内写上条件,两个出口分别对应终止条件成立与否,其中一个指向循环体,经过循环体回到判断框的入口处.
循环结构的设计步骤
循环结构的三要素
循环变量,循环体、循环的终止条件.
概念讲解
?判断
循环体
满足条件?
是
否
直到型
满足条件?
循环体
否
是
当型
概念讲解
区别:循环结构具有重复性;条件结构具有选择性,不重复性。
1.条件结构和循环结构有什么区别和联系?
联系:循环结构中一定包含条件结构,用于确定何时终止执行循环体;条件结构中不含循环结构.
例题分析
第四步,判断“i>100”是否成立.
若是,则输出S,结束算法;
否则,返回第二步.
第一步,令i=1,S=0.
第二步,计算S+i,仍用S表示.
第三步,计算i+1,仍用i表示.
思考1:计算1+2+3+…+100的值的算法,并画 出程序框图。
算法分析:
知识探究(一):循环结构的程序框图
第一步,令i=1,S=0.
第二步,计算S+i,仍用S表示.
第三步,计算i+1,仍用i表示.
例题分析
思考2:用直到型循环结构,上述算法的程序框图如何表示?
开始
i=1
i>100?
是
输出S
结束
S=0
i=i+1
S=S+i
否
例题分析
思考3:用当型循环结构,上述算法的程序框图如何表示?
开始
i=1
结束
输出S
否
是
S=0
S=S+i
i≤100?
i=i+1
第二步,判断i≤100是否成立.
若是,则执行第三步;
否则,输出S,结束算法.
第一步,令i=1,S=0.
第三步,计算S+i,仍用S表示.
第四步,计算i+1,仍用i表示,
返回第三步.
例题分析
思考4:观察两个程序框图,直到型循环结构与当型循环结构如何转化?
开始
i=1
i>100?
是
输出S
结束
S=0
i=i+1
S=S+i
否
开始
i=1
结束
输出S
否
是
S=0
i≤100?
i=i+1
S=S+i
初始值
循环体
终止条件
例题分析
变式1:右边的程序框图,
输出S=———?
开始
i=1
i>3?
是
输出S
结束
S=0
i=i+1
S=S+i2
否
14
例题分析
题型二:程序框图的补充
1、求 的值。设计的算法框图如右,应该在空格位置填入什么条件?
分析:空格位置判断条件,应该考虑循环的终止条件是什么?
应该填入:i>10
例题分析
结束
输出S
i=0;S=0
开始
S=S+i
i=i+1
i>10?
否
是
2.如图所示的程序框图运行后,输出的结果为
55
i=0, s=0
i=1, s=0+1
i=2, s=0+1+2
i=3, s=0+1+2+3
i=4, s=0+1+2+3+4
i=5, s=0+1+2+3+4+5
i=6, s=0+1+2+3+4+5+6
i=7, s=0+1+2+3+4+5+6+7
i=8, s=0+1+2+3+4+5+6+7+8
i=9, s=0+1+2+3+4+5+6+7+8+9
i=10,s=0+1+2+3+4+5+6+7+8+9+10
i=11,s=....
例题分析
跟踪训练
3.设计一算法,求积:
1×2×3×…×100,画出流程图.
结束
输出S
i=1,S=1
S=S*i
i = i + 1
i>100?
开始
第四步,判断“i>100”是否成立.
若是,则输出S,结束算法;
否则,返回第二步.
算法分析:
第一步,令i=1,S=1.
第二步,计算S*i,仍用S表示.
第三步,计算i+1,仍用i表示.
否
是
跟踪训练
解:算法步骤:
第一步,令i=1,s=0.
第二步,判断“i≤100”若成立,则执行第三步,否则,输出s.
第三步,计算s=s+i2
第四步,计算i=i+1,返回第二步.
开始
i=1
S=0
i=i+1
S=S+i2
i≤100?
输出S
结束
否
是
当型循环结构
2、P.20习题A组第2题
课堂小结:
3.设计一个算法的程序框图的基本思路:
第二步,确定每个算法步骤所包含的逻辑结构,并用相应的程序框图表示.
第一步,用自然语言表述算法步骤.
第三步,将所有步骤的程序框图用流程线连接起来,并加上两个终端框.
首先确定循环体,再根据循环体第一步确定初值,
最后一步确定循环终止条件。
1.循环结构三要素:
循环变量赋初值、循环体、循环终止条件
2.循环三要素确定过程:
课堂小结:
1、循环结构的特点
2、循环结构的框图表示
3、循环结构该注意的问题
避免死循环的出现,设置好进入(结束)循环体的条件。
当型和直到型
重复同一个处理过程
布置作业:
1.大本P8小试身手。
2.小本69页【基础达标练】
3.预习:循环结构(P12-P19)。
谢 谢 欣 赏!
