4.2.2等差数列的前n项和-课件(共36张PPT)-2020-2021学年高二上学期数学人教A版(2019)选择性必修第二册
文档属性
| 名称 | 4.2.2等差数列的前n项和-课件(共36张PPT)-2020-2021学年高二上学期数学人教A版(2019)选择性必修第二册 |  | |
| 格式 | pptx | ||
| 文件大小 | 655.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-29 15:07:57 | ||
图片预览




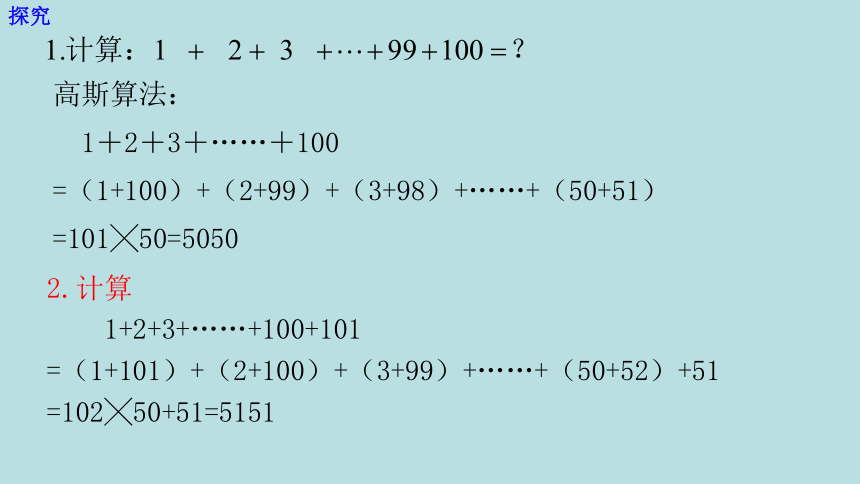
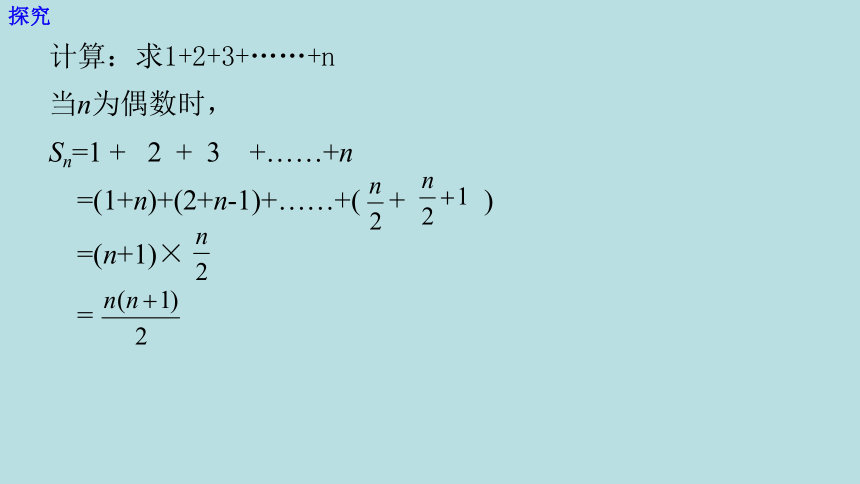

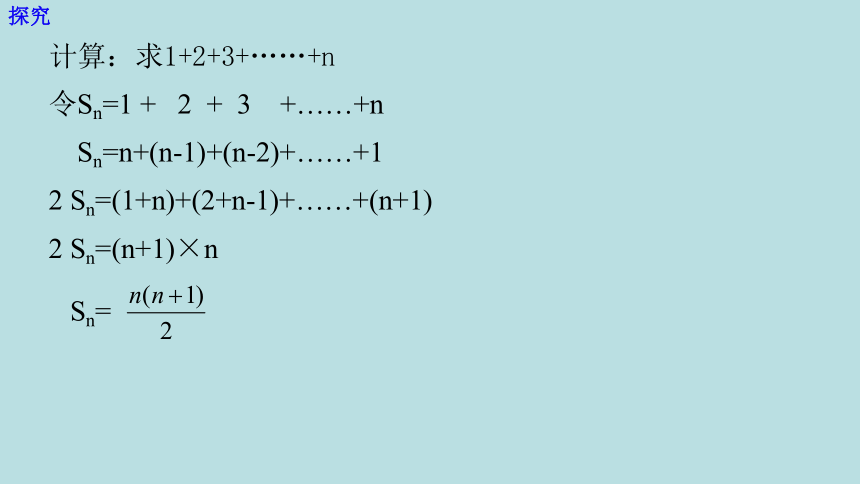

文档简介
4.2.2等差数列的前n项和
1.等差数列的定义
如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,这个数列就叫做等差数列。
这个常数叫做等差数列的公差,公差通常用字母d表示。
符号表示:an - an-1=d(n≥2,n∈N*)
2.首项a1公差d,的等差数列{an}的通项公式为
an=a1+(n-1)d=an=am+(n-m)d
复习
已知等差数列的任意两项可求公差
引入
据说,200多年前,高斯的算数老师提出了下面的问题:
1+2+3+...+99+100=?
当其他同学忙于把100个数逐个相加时,10岁的高斯却用下面的方法迅速算出了正确答案:
(1+100)+(2+99)+(3+98)+……+(50+51)=101╳50=5050
高斯的算法实际上解决了求等差数列1,2,3,...,n,...①前100项的和的问题
思考:你能说说高斯在求和过程中利用了数列①的什么性质吗?你能从中得到求数列①的前n项和的方法吗?
探究
思考:你能说说高斯在求和过程中利用了数列①的什么性质吗?你能从中得到求数列①的前n项和的方法吗?
解:对于数列①,设an=n,那么高斯的算法可表示为
(a1+a100)+(a2+a99)+...+(a50+a51)=101╳50=5050
可以发现,高斯利用了
a1+a100=a2+a99=...=a50+a51(下标和性质)
使不同数的求和问题转化为相同数(即101)的求和,从而简化运算
高斯算法:
1+2+3+……+100
=(1+100)+(2+99)+(3+98)+……+(50+51)
=101╳50=5050
2.计算
1+2+3+……+100+101
=(1+101)+(2+100)+(3+99)+……+(50+52)+51
=102╳50+51=5151
探究
计算:求1+2+3+……+n
当n为偶数时,
Sn=1 + 2 + 3 +……+n
=(1+n)+(2+n-1)+……+( + )
=(n+1)×
=
探究
当n为奇数时,
Sn=1 + 2 + 3 +……+n
=(1+n)+(2+n-1)+……+( + )+
=(n+1)× +
=
探究
计算:求1+2+3+……+n
思考:我们发现,在求前n个正整数的和时,要对n分奇数、偶数进行讨论,比较麻烦,能否设法避免分类讨论?
令Sn=1 + 2 + 3 +……+n
Sn=n+(n-1)+(n-2)+……+1
2 Sn=(1+n)+(2+n-1)+……+(n+1)
2 Sn=(n+1)×n
Sn=
探究
计算:求1+2+3+……+n
已知等差数列{ an }的首项为a1,项数是n,第n项为an,求前n项和Sn .
解:
①
②
倒序相加法
探究
于是有:
设等差数列{an}的前n项和为sn
公式一
公式二
探究
设等差数列{an}的前n项和为sn
公式一
公式二
练习:已知{an}是等差数列, 求Sn
(1)a1=1,an=2n-1
(2)a1=2,an=-3n+5
(3)a1=1,d=-2
(4)a1=-10,d=3
新知
例6 已知{an}是等差数列
(1)若a1=7,a50=101,求S50;(2)若a1=7,a2= ,求S10;
(3) 若a1= ,d= ,Sn=-5,求n.
(2)∵a1=2,a2= ,∴d=
例题
即n2-7n-60=0
解得n=12或n=-5(舍)
例6 已知{an}是等差数列
(1)若a1=7,a50=101,求S50;(2)若a1=7,a2= ,求S10;
(3) 若a1= ,d= ,Sn=-5,求n.
例题
已知{an}是等差数列, 求Sn
(1)a1=5,an=95,n=10
(2)a1=6,a12=-16
(3)a1=100,d=-2,n=50 (4)a1=2,d=2,n=10
练习
已知{an}是等差数列, 公差为d,求Sn
(1)a1=-4,a8=-18,n=10 (2)a1=14.5,d=0.7,an=32
练习
等差数列的前n项和公式的应用
1.当已知首项、末项和项数时,可采用公式一
当已知首项、公差和项数时,可采用公式二.
2.两个公式共涉及a1、d、n、an及Sn五个基本量,
知三求二。
归纳
例7.已知一个等差数列 前10项的和310,前20项的和是1220.有这些条件能确定这个等差数列的首项和公差吗?
解:设这个等差数列的公差为d,前n项和公式为Sn
由题意知 ,根据
所以
解得
所以这个等差数列的首项为4、公差为6
例题
一般地,对于等差数列,只要给定两个相互独立的条件,这个数列就完全确定
例8.某校新建一个报告厅,要求容纳800个座位,报告厅共有20排座位,从第2排起后一排都比前一排多2个座位.问第1排应安排多少个座位.
分析:等差数列,n=20,S20=800,d=2,求首项
解:设报告厅作为从第1排到第20排的座位数依次排成一列,构成等差数列{an}.记前n项和为Sn
则由题意可知,n=20,S20=800,d=2,
解得a1=21 因此第1排应安排21个座位
例题
举例:已知{an}是等差数列, 求Sn
(1)a1=1,an=2n-1
(2)a1=2,an=-3n+5
(3)a1=1,d=-2
(4)a1=-10,d=3
探究
Sn是关于n的二次函数式(常数项为0),Sn的图象是二次函数y=Ax2+Bx上的一群孤立的点.
结论: {an}为等差数列? ,这是一个关于 的
没有 的“ ”, ,
Sn=An2+Bn
n
常数项
二次函数
( 注意 A 还可以是 0)
新知
例9 已知等差数列{an}的前n项和为Sn,若a1=10,公差d=-2,则Sn是否存在最大值?若存在,求Sn的最大值及取得最大值时n的值;若不存在,请说明理由.
分析:Sn是关于n的没有常数项的一元二次函数,这样,就把求Sn的最大值转化为求二次函数得最大值.
解:因为a1=10,公差d=-2
即Sn=-n2+11n,
∵f(x)=-x2+9x在x=5.5时取得最大值
∴当n=5或6时取得最大值,最大值为30
例题
例9 已知等差数列{an}的前n项和为Sn,若a1=10,公差d=-2,则Sn是否存在最大值?若存在,求Sn的最大值及取得最大值时n的值;若不存在,请说明理由.
解:∵a1=10,公差d=-2,
∴{an}是递减数列,且an=a1+(n-1)d=10+(n-1)×(-2)=-2n+12
令-2n+12>0得n<6
令-2n+12=0得n=6
令-2n+12<0得n>6
∴当n=5或6时取得最大值
例题
求等差数列前n项和的最值的2种方法
(1)通项公式法:利用等差数列的单调性,求出其正负转折项.即求使an≥0(或an≤0)成立的最大n值,即得Sn的最值.
(2)二次函数法
利用等差数列的前n项和Sn=An2+Bn(A、B为常数)为二次函数,运用配方法,借助函数的单调性及数形结合求最值.
此种方法需要注意“自变量n为正整数”这一隐含条件,若对称轴取不到,需考虑最接近对称轴的自变量n(n∈N*).
归纳
设等差数列{an}的前n项和为Sn,若a1=-11,a4+a6=-6,则当Sn取最小值时,n等于( )
A.6 B.7 C.8 D.9
练习
[解析]解法一:设该数列的公差为d,
则a4+a6=2a1+8d=2×(-11)+8d=-6,解得d=2,
所以Sn=-11n+ =n2-12n=(n-6)2-36,
所以当n=6时,Sn取最小值.
解法二:
由an=2n-13知,n≤6时,an<0;n≥7时,an>0,故S6最小.
小结
1.设等差数列{an}的前n项和为sn
公式一
公式二
2.{an}为等差数列?Sn=An2+Bn,这是一个关于n的没有常数项
的二次函数,其中
3.求等差数列前n项和的最值的2种方法
(1)通项公式法:利用等差数列的单调性,求出其正负转折项.即求使an≥0(或an≤0)成立的最大n值,即得Sn的最值.
(2)二次函数法
作业
P24课本习题4.2 1、2
1.等差数列的定义
如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,这个数列就叫做等差数列。
这个常数叫做等差数列的公差,公差通常用字母d表示。
符号表示:an - an-1=d(n≥2,n∈N*)
2.首项a1公差d,的等差数列{an}的通项公式为
an=a1+(n-1)d=an=am+(n-m)d
复习
已知等差数列的任意两项可求公差
引入
据说,200多年前,高斯的算数老师提出了下面的问题:
1+2+3+...+99+100=?
当其他同学忙于把100个数逐个相加时,10岁的高斯却用下面的方法迅速算出了正确答案:
(1+100)+(2+99)+(3+98)+……+(50+51)=101╳50=5050
高斯的算法实际上解决了求等差数列1,2,3,...,n,...①前100项的和的问题
思考:你能说说高斯在求和过程中利用了数列①的什么性质吗?你能从中得到求数列①的前n项和的方法吗?
探究
思考:你能说说高斯在求和过程中利用了数列①的什么性质吗?你能从中得到求数列①的前n项和的方法吗?
解:对于数列①,设an=n,那么高斯的算法可表示为
(a1+a100)+(a2+a99)+...+(a50+a51)=101╳50=5050
可以发现,高斯利用了
a1+a100=a2+a99=...=a50+a51(下标和性质)
使不同数的求和问题转化为相同数(即101)的求和,从而简化运算
高斯算法:
1+2+3+……+100
=(1+100)+(2+99)+(3+98)+……+(50+51)
=101╳50=5050
2.计算
1+2+3+……+100+101
=(1+101)+(2+100)+(3+99)+……+(50+52)+51
=102╳50+51=5151
探究
计算:求1+2+3+……+n
当n为偶数时,
Sn=1 + 2 + 3 +……+n
=(1+n)+(2+n-1)+……+( + )
=(n+1)×
=
探究
当n为奇数时,
Sn=1 + 2 + 3 +……+n
=(1+n)+(2+n-1)+……+( + )+
=(n+1)× +
=
探究
计算:求1+2+3+……+n
思考:我们发现,在求前n个正整数的和时,要对n分奇数、偶数进行讨论,比较麻烦,能否设法避免分类讨论?
令Sn=1 + 2 + 3 +……+n
Sn=n+(n-1)+(n-2)+……+1
2 Sn=(1+n)+(2+n-1)+……+(n+1)
2 Sn=(n+1)×n
Sn=
探究
计算:求1+2+3+……+n
已知等差数列{ an }的首项为a1,项数是n,第n项为an,求前n项和Sn .
解:
①
②
倒序相加法
探究
于是有:
设等差数列{an}的前n项和为sn
公式一
公式二
探究
设等差数列{an}的前n项和为sn
公式一
公式二
练习:已知{an}是等差数列, 求Sn
(1)a1=1,an=2n-1
(2)a1=2,an=-3n+5
(3)a1=1,d=-2
(4)a1=-10,d=3
新知
例6 已知{an}是等差数列
(1)若a1=7,a50=101,求S50;(2)若a1=7,a2= ,求S10;
(3) 若a1= ,d= ,Sn=-5,求n.
(2)∵a1=2,a2= ,∴d=
例题
即n2-7n-60=0
解得n=12或n=-5(舍)
例6 已知{an}是等差数列
(1)若a1=7,a50=101,求S50;(2)若a1=7,a2= ,求S10;
(3) 若a1= ,d= ,Sn=-5,求n.
例题
已知{an}是等差数列, 求Sn
(1)a1=5,an=95,n=10
(2)a1=6,a12=-16
(3)a1=100,d=-2,n=50 (4)a1=2,d=2,n=10
练习
已知{an}是等差数列, 公差为d,求Sn
(1)a1=-4,a8=-18,n=10 (2)a1=14.5,d=0.7,an=32
练习
等差数列的前n项和公式的应用
1.当已知首项、末项和项数时,可采用公式一
当已知首项、公差和项数时,可采用公式二.
2.两个公式共涉及a1、d、n、an及Sn五个基本量,
知三求二。
归纳
例7.已知一个等差数列 前10项的和310,前20项的和是1220.有这些条件能确定这个等差数列的首项和公差吗?
解:设这个等差数列的公差为d,前n项和公式为Sn
由题意知 ,根据
所以
解得
所以这个等差数列的首项为4、公差为6
例题
一般地,对于等差数列,只要给定两个相互独立的条件,这个数列就完全确定
例8.某校新建一个报告厅,要求容纳800个座位,报告厅共有20排座位,从第2排起后一排都比前一排多2个座位.问第1排应安排多少个座位.
分析:等差数列,n=20,S20=800,d=2,求首项
解:设报告厅作为从第1排到第20排的座位数依次排成一列,构成等差数列{an}.记前n项和为Sn
则由题意可知,n=20,S20=800,d=2,
解得a1=21 因此第1排应安排21个座位
例题
举例:已知{an}是等差数列, 求Sn
(1)a1=1,an=2n-1
(2)a1=2,an=-3n+5
(3)a1=1,d=-2
(4)a1=-10,d=3
探究
Sn是关于n的二次函数式(常数项为0),Sn的图象是二次函数y=Ax2+Bx上的一群孤立的点.
结论: {an}为等差数列? ,这是一个关于 的
没有 的“ ”, ,
Sn=An2+Bn
n
常数项
二次函数
( 注意 A 还可以是 0)
新知
例9 已知等差数列{an}的前n项和为Sn,若a1=10,公差d=-2,则Sn是否存在最大值?若存在,求Sn的最大值及取得最大值时n的值;若不存在,请说明理由.
分析:Sn是关于n的没有常数项的一元二次函数,这样,就把求Sn的最大值转化为求二次函数得最大值.
解:因为a1=10,公差d=-2
即Sn=-n2+11n,
∵f(x)=-x2+9x在x=5.5时取得最大值
∴当n=5或6时取得最大值,最大值为30
例题
例9 已知等差数列{an}的前n项和为Sn,若a1=10,公差d=-2,则Sn是否存在最大值?若存在,求Sn的最大值及取得最大值时n的值;若不存在,请说明理由.
解:∵a1=10,公差d=-2,
∴{an}是递减数列,且an=a1+(n-1)d=10+(n-1)×(-2)=-2n+12
令-2n+12>0得n<6
令-2n+12=0得n=6
令-2n+12<0得n>6
∴当n=5或6时取得最大值
例题
求等差数列前n项和的最值的2种方法
(1)通项公式法:利用等差数列的单调性,求出其正负转折项.即求使an≥0(或an≤0)成立的最大n值,即得Sn的最值.
(2)二次函数法
利用等差数列的前n项和Sn=An2+Bn(A、B为常数)为二次函数,运用配方法,借助函数的单调性及数形结合求最值.
此种方法需要注意“自变量n为正整数”这一隐含条件,若对称轴取不到,需考虑最接近对称轴的自变量n(n∈N*).
归纳
设等差数列{an}的前n项和为Sn,若a1=-11,a4+a6=-6,则当Sn取最小值时,n等于( )
A.6 B.7 C.8 D.9
练习
[解析]解法一:设该数列的公差为d,
则a4+a6=2a1+8d=2×(-11)+8d=-6,解得d=2,
所以Sn=-11n+ =n2-12n=(n-6)2-36,
所以当n=6时,Sn取最小值.
解法二:
由an=2n-13知,n≤6时,an<0;n≥7时,an>0,故S6最小.
小结
1.设等差数列{an}的前n项和为sn
公式一
公式二
2.{an}为等差数列?Sn=An2+Bn,这是一个关于n的没有常数项
的二次函数,其中
3.求等差数列前n项和的最值的2种方法
(1)通项公式法:利用等差数列的单调性,求出其正负转折项.即求使an≥0(或an≤0)成立的最大n值,即得Sn的最值.
(2)二次函数法
作业
P24课本习题4.2 1、2
