2021——2022学年华东师大版八年级数学上册第14章 勾股定理单元测试题(word版含答案)
文档属性
| 名称 | 2021——2022学年华东师大版八年级数学上册第14章 勾股定理单元测试题(word版含答案) | 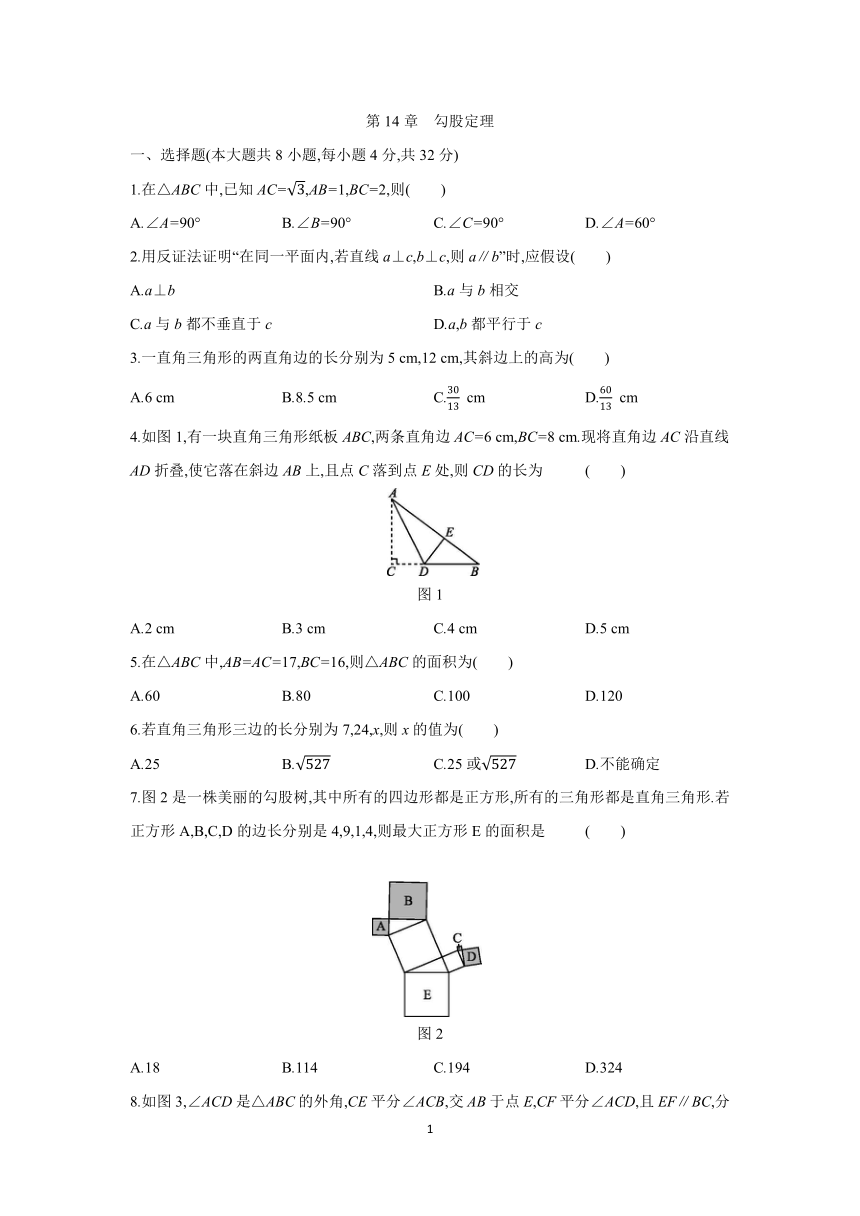 | |
| 格式 | zip | ||
| 文件大小 | 133.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-30 06:39:34 | ||
图片预览



文档简介
第14章 勾股定理
一、选择题(本大题共8小题,每小题4分,共32分)
1.在△ABC中,已知AC=,AB=1,BC=2,则( )
A.∠A=90°
B.∠B=90°
C.∠C=90°
D.∠A=60°
2.用反证法证明“在同一平面内,若直线a⊥c,b⊥c,则a∥b”时,应假设( )
A.a⊥b
B.a与b相交
C.a与b都不垂直于c
D.a,b都平行于c
3.一直角三角形的两直角边的长分别为5
cm,12
cm,其斜边上的高为( )
A.6
cm
B.8.5
cm
C.
cm
D.
cm
4.如图1,有一块直角三角形纸板ABC,两条直角边AC=6
cm,BC=8
cm.现将直角边AC沿直线AD折叠,使它落在斜边AB上,且点C落到点E处,则CD的长为
( )
图1
A.2
cm
B.3
cm
C.4
cm
D.5
cm
5.在△ABC中,AB=AC=17,BC=16,则△ABC的面积为( )
A.60
B.80
C.100
D.120
6.若直角三角形三边的长分别为7,24,x,则x的值为( )
A.25
B.
C.25或
D.不能确定
7.图2是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A,B,C,D的边长分别是4,9,1,4,则最大正方形E的面积是
( )
图2
A.18
B.114
C.194
D.324
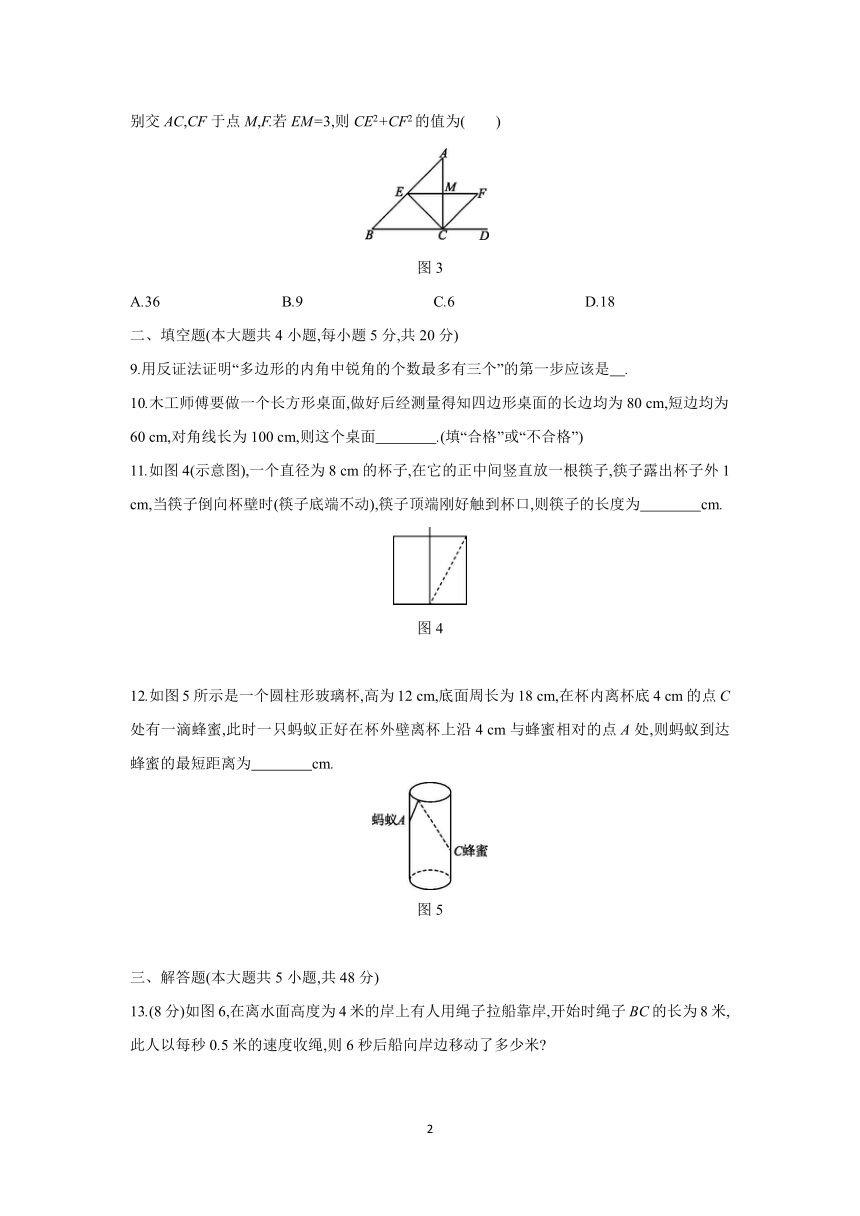
8.如图3,∠ACD是△ABC的外角,CE平分∠ACB,交AB于点E,CF平分∠ACD,且EF∥BC,分别交AC,CF于点M,F.若EM=3,则CE2+CF2的值为( )
图3
A.36
B.9
C.6
D.18
二、填空题(本大题共4小题,每小题5分,共20分)
9.用反证法证明“多边形的内角中锐角的个数最多有三个”的第一步应该是 .?
10.木工师傅要做一个长方形桌面,做好后经测量得知四边形桌面的长边均为80
cm,短边均为60
cm,对角线长为100
cm,则这个桌面 .(填“合格”或“不合格”)?
11.如图4(示意图),一个直径为8
cm的杯子,在它的正中间竖直放一根筷子,筷子露出杯子外1
cm,当筷子倒向杯壁时(筷子底端不动),筷子顶端刚好触到杯口,则筷子的长度为 cm.?
图4
12.如图5所示是一个圆柱形玻璃杯,高为12
cm,底面周长为18
cm,在杯内离杯底4
cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁离杯上沿4
cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为 cm.?
图5
三、解答题(本大题共5小题,共48分)
13.(8分)如图6,在离水面高度为4米的岸上有人用绳子拉船靠岸,开始时绳子BC的长为8米,此人以每秒0.5米的速度收绳,则6秒后船向岸边移动了多少米?
图6
14.(8分)如图7,在△ABC中,AD⊥BC于点D,且AC+AD=32,BD=5,CD=16,试确定AB的长.
图7
15.(10分)王老师在一次“探究性学习”课中,设计了如下数表:
n
2
3
4
5
…
a
22-1
32-1
42-1
52-1
…
b
4
6
8
10
…
c
22+1
32+1
42+1
52+1
…
(1)请你观察数表中a,b,c与n之间的关系,并用含自然数n(n>1)的代数式表示:
a= ,b= ,c= ;?
(2)猜想:以a,b,c为三边长的三角形是不是直角三角形?请说明理由.
16.(10分)如图8,快乐农庄有一段斜坡BC长为10米,坡角∠CBD>45°,较为陡峭,为了方便通行,现准备把坡角减小.已知CD=8米,BD=6米,AB=9米,求斜坡新起点A与点C的距离.
图8
17.(12分)某机床内有两个小滑块A,B,由一根连杆连结,A,B分别可以在互相垂直的两个滑道上滑动.
(1)如图9①,开始时滑块A距O点16厘米,滑块B距O点12厘米,求连杆AB的长;
(2)在(1)的条件下,当机械运转时,如图②,如果滑块A向下滑动6厘米,求滑块B向外滑动了多少厘米.
图9
答案
1.[解析]
A ∵12+()2=22,∴AB2+AC2=BC2,∴∠A=90°.故选A.
2.B 3.D
4.[解析]
B 由题意可知,△ACD和△AED关于直线AD对称,因而△ACD≌△AED.进一步则有AE=AC=6
cm,CD=ED,ED⊥AB.设CD=ED=x
cm,在Rt△ABC中,由勾股定理可得AB2=AC2+BC2=62+82=100,得AB=10
cm.在Rt△BDE中,有x2+(10-6)2=(8-x)2,解得x=3.故CD=3
cm.
5.[解析]
D 如图,过点A作AD⊥BC于点D.
∵在△ABC中,AB=AC=17,BC=16,
∴BD=BC=8,
∴在Rt△ABD中,由勾股定理,得AD==15,
∴S△ABC=×16×15=120.故选D.
6.[解析]
C x可能为斜边长,也可能是直角边长,所以分两种情况讨论:x==25或x==.
7.[解析]
B 根据勾股定理的几何意义,可得A,B的面积和为S1,C,D的面积和为S2,S1=42+92,S2=12+42,则S3=S1+S2,∴S3=16+81+1+16=114.故选B.
8.[解析]
A 如图,∵CE平分∠ACB,CF平分∠ACD,
∴∠1=∠2=∠ACB,∠3=∠4=∠ACD,
∴∠2+∠3=(∠ACB+∠ACD)=90°,
∴△CEF是直角三角形.
∵EF∥BC,∴∠1=∠5,∠4=∠F,
∴∠2=∠5,∠3=∠F,∴EM=CM,CM=MF.
∵EM=3,∴EF=3+3=6.
在Rt△CEF中,CE2+CF2=EF2=62=36.
故选A.
9.假设多边形的内角中锐角的个数至少有四个 10.合格
11.[答案]
8.5
[解析]
设杯子的高度是x
cm,那么筷子的长度是(x+1)cm.
由题意,得x2+42=(x+1)2,解得x=7.5,
∴x+1=8.5,
∴筷子的长度为8.5
cm.
故答案为8.5.
12.15
13.解:在Rt△ABC中,BC=8米,AC=4米,
则AB===(米),
设6秒后,点B到达点B'处,则B'C=5米,
∴AB'===3(米),
故6秒后船向岸边移动了(-3)米.
14.解:由题意,设AD=x,则AC=32-x.
∵AD⊥BC,
∴△ADC和△ADB都是直角三角形.
∵CD=16,
∴x2+162=(32-x)2,
解得x=12,∴AD=12.
在Rt△ADB中,由勾股定理,得AB===13.
15.解:(1)n2-1 2n n2+1
(2)是直角三角形.
理由:因为a2=(n2-1)2=n4-2n2+1,b2=(2n)2=4n2,c2=(n2+1)2=n4+2n2+1,
而n4-2n2+1+4n2=n4+2n2+1,
即a2+b2=c2,
所以以a,b,c为三边长的三角形是直角三角形.
16.解:因为CD2+BD2=82+62=100=102=BC2,
所以△BDC是直角三角形,且∠BDC=90°.
在Rt△ACD中,AC2=CD2+AD2=82+(9+6)2=289=172,
所以AC=17米,
所以斜坡新起点A与点C的距离为17米.
17.解:(1)由题意,得OA=16厘米,OB=12厘米.
在Rt△AOB中,AB===20(厘米),
∴连杆AB的长为20厘米.
(2)由(1)得,CD=AB=20厘米.
∵AC=6厘米,
∴OC=OA-AC=10(厘米).
在Rt△COD中,OD===(厘米),
∴BD=OD-OB=(-12)厘米,
∴滑块B向外滑动了(-12)厘米.
(
1
)
一、选择题(本大题共8小题,每小题4分,共32分)
1.在△ABC中,已知AC=,AB=1,BC=2,则( )
A.∠A=90°
B.∠B=90°
C.∠C=90°
D.∠A=60°
2.用反证法证明“在同一平面内,若直线a⊥c,b⊥c,则a∥b”时,应假设( )
A.a⊥b
B.a与b相交
C.a与b都不垂直于c
D.a,b都平行于c
3.一直角三角形的两直角边的长分别为5
cm,12
cm,其斜边上的高为( )
A.6
cm
B.8.5
cm
C.
cm
D.
cm
4.如图1,有一块直角三角形纸板ABC,两条直角边AC=6
cm,BC=8
cm.现将直角边AC沿直线AD折叠,使它落在斜边AB上,且点C落到点E处,则CD的长为
( )
图1
A.2
cm
B.3
cm
C.4
cm
D.5
cm
5.在△ABC中,AB=AC=17,BC=16,则△ABC的面积为( )
A.60
B.80
C.100
D.120
6.若直角三角形三边的长分别为7,24,x,则x的值为( )
A.25
B.
C.25或
D.不能确定
7.图2是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A,B,C,D的边长分别是4,9,1,4,则最大正方形E的面积是
( )
图2
A.18
B.114
C.194
D.324
8.如图3,∠ACD是△ABC的外角,CE平分∠ACB,交AB于点E,CF平分∠ACD,且EF∥BC,分别交AC,CF于点M,F.若EM=3,则CE2+CF2的值为( )
图3
A.36
B.9
C.6
D.18
二、填空题(本大题共4小题,每小题5分,共20分)
9.用反证法证明“多边形的内角中锐角的个数最多有三个”的第一步应该是 .?
10.木工师傅要做一个长方形桌面,做好后经测量得知四边形桌面的长边均为80
cm,短边均为60
cm,对角线长为100
cm,则这个桌面 .(填“合格”或“不合格”)?
11.如图4(示意图),一个直径为8
cm的杯子,在它的正中间竖直放一根筷子,筷子露出杯子外1
cm,当筷子倒向杯壁时(筷子底端不动),筷子顶端刚好触到杯口,则筷子的长度为 cm.?
图4
12.如图5所示是一个圆柱形玻璃杯,高为12
cm,底面周长为18
cm,在杯内离杯底4
cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁离杯上沿4
cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为 cm.?
图5
三、解答题(本大题共5小题,共48分)
13.(8分)如图6,在离水面高度为4米的岸上有人用绳子拉船靠岸,开始时绳子BC的长为8米,此人以每秒0.5米的速度收绳,则6秒后船向岸边移动了多少米?
图6
14.(8分)如图7,在△ABC中,AD⊥BC于点D,且AC+AD=32,BD=5,CD=16,试确定AB的长.
图7
15.(10分)王老师在一次“探究性学习”课中,设计了如下数表:
n
2
3
4
5
…
a
22-1
32-1
42-1
52-1
…
b
4
6
8
10
…
c
22+1
32+1
42+1
52+1
…
(1)请你观察数表中a,b,c与n之间的关系,并用含自然数n(n>1)的代数式表示:
a= ,b= ,c= ;?
(2)猜想:以a,b,c为三边长的三角形是不是直角三角形?请说明理由.
16.(10分)如图8,快乐农庄有一段斜坡BC长为10米,坡角∠CBD>45°,较为陡峭,为了方便通行,现准备把坡角减小.已知CD=8米,BD=6米,AB=9米,求斜坡新起点A与点C的距离.
图8
17.(12分)某机床内有两个小滑块A,B,由一根连杆连结,A,B分别可以在互相垂直的两个滑道上滑动.
(1)如图9①,开始时滑块A距O点16厘米,滑块B距O点12厘米,求连杆AB的长;
(2)在(1)的条件下,当机械运转时,如图②,如果滑块A向下滑动6厘米,求滑块B向外滑动了多少厘米.
图9
答案
1.[解析]
A ∵12+()2=22,∴AB2+AC2=BC2,∴∠A=90°.故选A.
2.B 3.D
4.[解析]
B 由题意可知,△ACD和△AED关于直线AD对称,因而△ACD≌△AED.进一步则有AE=AC=6
cm,CD=ED,ED⊥AB.设CD=ED=x
cm,在Rt△ABC中,由勾股定理可得AB2=AC2+BC2=62+82=100,得AB=10
cm.在Rt△BDE中,有x2+(10-6)2=(8-x)2,解得x=3.故CD=3
cm.
5.[解析]
D 如图,过点A作AD⊥BC于点D.
∵在△ABC中,AB=AC=17,BC=16,
∴BD=BC=8,
∴在Rt△ABD中,由勾股定理,得AD==15,
∴S△ABC=×16×15=120.故选D.
6.[解析]
C x可能为斜边长,也可能是直角边长,所以分两种情况讨论:x==25或x==.
7.[解析]
B 根据勾股定理的几何意义,可得A,B的面积和为S1,C,D的面积和为S2,S1=42+92,S2=12+42,则S3=S1+S2,∴S3=16+81+1+16=114.故选B.
8.[解析]
A 如图,∵CE平分∠ACB,CF平分∠ACD,
∴∠1=∠2=∠ACB,∠3=∠4=∠ACD,
∴∠2+∠3=(∠ACB+∠ACD)=90°,
∴△CEF是直角三角形.
∵EF∥BC,∴∠1=∠5,∠4=∠F,
∴∠2=∠5,∠3=∠F,∴EM=CM,CM=MF.
∵EM=3,∴EF=3+3=6.
在Rt△CEF中,CE2+CF2=EF2=62=36.
故选A.
9.假设多边形的内角中锐角的个数至少有四个 10.合格
11.[答案]
8.5
[解析]
设杯子的高度是x
cm,那么筷子的长度是(x+1)cm.
由题意,得x2+42=(x+1)2,解得x=7.5,
∴x+1=8.5,
∴筷子的长度为8.5
cm.
故答案为8.5.
12.15
13.解:在Rt△ABC中,BC=8米,AC=4米,
则AB===(米),
设6秒后,点B到达点B'处,则B'C=5米,
∴AB'===3(米),
故6秒后船向岸边移动了(-3)米.
14.解:由题意,设AD=x,则AC=32-x.
∵AD⊥BC,
∴△ADC和△ADB都是直角三角形.
∵CD=16,
∴x2+162=(32-x)2,
解得x=12,∴AD=12.
在Rt△ADB中,由勾股定理,得AB===13.
15.解:(1)n2-1 2n n2+1
(2)是直角三角形.
理由:因为a2=(n2-1)2=n4-2n2+1,b2=(2n)2=4n2,c2=(n2+1)2=n4+2n2+1,
而n4-2n2+1+4n2=n4+2n2+1,
即a2+b2=c2,
所以以a,b,c为三边长的三角形是直角三角形.
16.解:因为CD2+BD2=82+62=100=102=BC2,
所以△BDC是直角三角形,且∠BDC=90°.
在Rt△ACD中,AC2=CD2+AD2=82+(9+6)2=289=172,
所以AC=17米,
所以斜坡新起点A与点C的距离为17米.
17.解:(1)由题意,得OA=16厘米,OB=12厘米.
在Rt△AOB中,AB===20(厘米),
∴连杆AB的长为20厘米.
(2)由(1)得,CD=AB=20厘米.
∵AC=6厘米,
∴OC=OA-AC=10(厘米).
在Rt△COD中,OD===(厘米),
∴BD=OD-OB=(-12)厘米,
∴滑块B向外滑动了(-12)厘米.
(
1
)
