2021——2022学年京改版八年级数学上册第十二章 三角形 单元测试题(word版含答案)
文档属性
| 名称 | 2021——2022学年京改版八年级数学上册第十二章 三角形 单元测试题(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 183.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-30 00:00:00 | ||
图片预览


文档简介
第十二章 三角形
一、选择题(本大题共7小题,每小题4分,共28分)
1.篆体是我国古代汉字书体之一.下列篆体字“复”“兴”“之”“路”中,是轴对称图形的为( )
图1
2.如图2,为估计假山A,B两端的距离,小明在一侧选取了一点C,测得AC=18
m,BC=12
m,那么A,B之间的距离不可能是( )
A.12
m
B.16
m
C.18
m
D.30
m
图2
图3
3.如图3,已知∠A=32°,∠B=45°,∠C=38°,则∠DFE的度数为( )
A.105°
B.110°
C.115°
D.120°
4.已知等腰三角形的一个内角为75°,则其顶角为( )
A.30°
B.75°
C.105°
D.30°或75°
5.如图4,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=10,则PD的长为( )
图4
A.10
B.5
C.5
D.2.5
6.有下列条件:①∠A+∠B=∠C;②∠A∶∠B∶∠C
=1∶2∶3;③三边分别为a,b,c且a∶b∶c=1∶2∶;④∠A=∠B=∠C.其中能确定△ABC是直角三角形的条件有( )
A.1个
B.2个
C.3个
D.
4个
7.“白日登山望烽火,黄昏饮马傍交河.”诗中隐含着一个有趣的数学问题:如图5,诗中将军在观望烽火之后从山脚下的点A出发,奔向小河旁边的点P饮马,饮马后再到点B宿营,若点A,B到水平直线l(l表示小河)的距离分别是3,1,A,B两点之间的水平距离是3,则AP+PB的最小值为( )
图5
A.3
B.4
C.5
D.6
二、填空题(本大题共6小题,每小题5分,共30分)
8.为了使一扇旧木门不变形,木工师傅在木门的背面加钉了一根如图6所示的木条,这样做的道理是
.?
图6
图7
9.如图7,在△ABC中,∠B=67°,∠C=33°,AD是△ABC的角平分线,则∠CAD的度数为 .?
10.已知三组数据:(1)2,4,3;(2)3,4,5;(3)1,,2.分别以每组数据中的三个数作为三角形的三边长,可以构成直角三角形的有
.(填序号)?
11.三角形的三边长分别为5,1+2x,8,则x的取值范围是 .?
12.如图8,已知点A,D,B,F在一条直线上,AC=EF,AD=BF,要使△ABC≌△FDE,还需添加一个条件,这个条件可以是 .(只需填一个即可)?
图8
图9
13.如图9,在△ABC中,∠ABC<20°,三边长分别为a,b,c.将△ABC沿直线BA翻折,得到△ABC1;然后将△ABC1沿直线BC1翻折,得到△A1BC1;再将△A1BC1沿直线A1B翻折,得到△A1BC2……翻折4次后,所得图形A2BCAC1A1C2的周长为 ,翻折15次后,所得图形的周长为
.(结果用含a,b,c的式子表示)?
三、解答题(共42分)
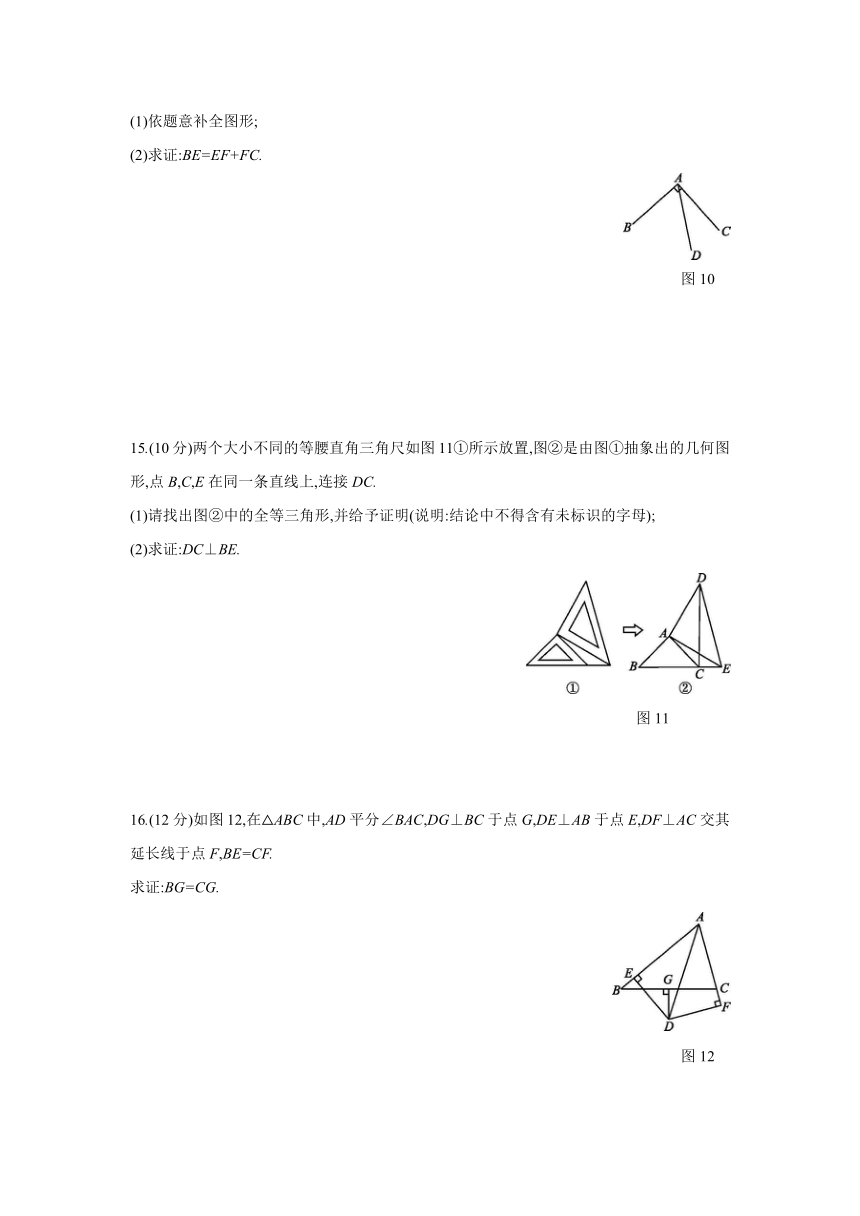
14.(8分)如图10,AB⊥AC,AB=AC,过点B,C分别向射线AD作垂线,垂足分别为E,F.
(1)依题意补全图形;
(2)求证:BE=EF+FC.
图10
15.(10分)两个大小不同的等腰直角三角尺如图11①所示放置,图②是由图①抽象出的几何图形,点B,C,E在同一条直线上,连接DC.
(1)请找出图②中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母);
(2)求证:DC⊥BE.
图11
16.(12分)如图12,在△ABC中,AD平分∠BAC,DG⊥BC于点G,DE⊥AB于点E,DF⊥AC交其延长线于点F,BE=CF.
求证:BG=CG.
图12
17.(12分)如图13,在△ABC中,AB=AC,点M在△ABC内,AM平分∠BAC,点D与点M在AC所在直线的两侧,AD⊥AB,AD=BC,点E在AC边上,CE=AM,连接MD,BE.
(1)依题意补全图形.
(2)请判断MD与BE的数量关系,并进行证明.
(3)点M在何处时,BM+BE会有最小值,画出图形确定点M的位置;如果AB=5,BC=6,求出BM+BE的最小值.
图13
答案
1.B 2.D 3.C 4.D 5.C 6.D 7.C
8.三角形的稳定性
9.40° 10.(2)(3)
11.1由三角形三边关系得8-5<1+2x<8+5,解得112.∠A=∠F或AC∥EF等(答案不唯一)
13.a+c+5b 2a+16b
14.解:(1)补全图形如图.
(2)证明:∵AB⊥AC,BE⊥AD,CF⊥AD,
∴∠BAE+∠CAF=90°,∠BAE+∠B=90°,∠CFA=∠AEB=90°.
∴∠CAF=∠B.
在△ABE和△CAF中,
∴△ABE≌△CAF(AAS).
∴BE=AF,AE=CF.
∵AF=AE+EF,
∴BE=EF+CF.
15.解:(1)△BAE≌△CAD.
证明如下:
∵∠BAC=∠DAE=90°,
∴∠BAE=∠CAD.
又∵AB=AC,AE=AD,
∴△BAE≌△CAD.
(2)证明:∵△BAE≌△CAD,
∴∠BEA=∠CDA.
又∵∠ADE=45°,
∴∠BEA+∠CDE=45°.
又∵∠DEA=45°,
∴∠CDE+∠DEC=90°.
∴∠BCD=90°,
即DC⊥BE.
16.证明:连接BD,CD.
∵AD平分∠BAC,DE⊥AB于点E,DF⊥AC交其延长线于点F,
∴DE=DF.
在△DEB和△DFC中,
∴△DEB≌△DFC.
∴DB=DC.
又∵DG⊥BC,
∴BG=CG.
17.解:(1)补全图形如图①.
(2)MD=BE.
证明:延长AM交BC于点F,如图②.
∵AM平分∠BAC,
∴∠BAM=∠CAM.
∵AD⊥AB,∴∠MAD+∠BAM=90°.
∴∠MAD+∠CAM=90°.
∵AB=AC,AM平分∠BAC,∴AF⊥BC.
∴∠C+∠CAM=90°.
∴∠MAD=∠C.
又∵AM=CE,AD=BC,
∴△AMD≌△CEB.
∴MD=BE.
(3)由(2)可知,BM+BE=BM+MD,根据两点之间线段最短,连接BD,BD与AM所在直线的交点即为点M的位置,如图③所示.
∵AD=BC,BC=6,
∴AD=BC=6.
∴在Rt△ABD中,BD===.
∴BM+BE的最小值为.
一、选择题(本大题共7小题,每小题4分,共28分)
1.篆体是我国古代汉字书体之一.下列篆体字“复”“兴”“之”“路”中,是轴对称图形的为( )
图1
2.如图2,为估计假山A,B两端的距离,小明在一侧选取了一点C,测得AC=18
m,BC=12
m,那么A,B之间的距离不可能是( )
A.12
m
B.16
m
C.18
m
D.30
m
图2
图3
3.如图3,已知∠A=32°,∠B=45°,∠C=38°,则∠DFE的度数为( )
A.105°
B.110°
C.115°
D.120°
4.已知等腰三角形的一个内角为75°,则其顶角为( )
A.30°
B.75°
C.105°
D.30°或75°
5.如图4,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=10,则PD的长为( )
图4
A.10
B.5
C.5
D.2.5
6.有下列条件:①∠A+∠B=∠C;②∠A∶∠B∶∠C
=1∶2∶3;③三边分别为a,b,c且a∶b∶c=1∶2∶;④∠A=∠B=∠C.其中能确定△ABC是直角三角形的条件有( )
A.1个
B.2个
C.3个
D.
4个
7.“白日登山望烽火,黄昏饮马傍交河.”诗中隐含着一个有趣的数学问题:如图5,诗中将军在观望烽火之后从山脚下的点A出发,奔向小河旁边的点P饮马,饮马后再到点B宿营,若点A,B到水平直线l(l表示小河)的距离分别是3,1,A,B两点之间的水平距离是3,则AP+PB的最小值为( )
图5
A.3
B.4
C.5
D.6
二、填空题(本大题共6小题,每小题5分,共30分)
8.为了使一扇旧木门不变形,木工师傅在木门的背面加钉了一根如图6所示的木条,这样做的道理是
.?
图6
图7
9.如图7,在△ABC中,∠B=67°,∠C=33°,AD是△ABC的角平分线,则∠CAD的度数为 .?
10.已知三组数据:(1)2,4,3;(2)3,4,5;(3)1,,2.分别以每组数据中的三个数作为三角形的三边长,可以构成直角三角形的有
.(填序号)?
11.三角形的三边长分别为5,1+2x,8,则x的取值范围是 .?
12.如图8,已知点A,D,B,F在一条直线上,AC=EF,AD=BF,要使△ABC≌△FDE,还需添加一个条件,这个条件可以是 .(只需填一个即可)?
图8
图9
13.如图9,在△ABC中,∠ABC<20°,三边长分别为a,b,c.将△ABC沿直线BA翻折,得到△ABC1;然后将△ABC1沿直线BC1翻折,得到△A1BC1;再将△A1BC1沿直线A1B翻折,得到△A1BC2……翻折4次后,所得图形A2BCAC1A1C2的周长为 ,翻折15次后,所得图形的周长为
.(结果用含a,b,c的式子表示)?
三、解答题(共42分)
14.(8分)如图10,AB⊥AC,AB=AC,过点B,C分别向射线AD作垂线,垂足分别为E,F.
(1)依题意补全图形;
(2)求证:BE=EF+FC.
图10
15.(10分)两个大小不同的等腰直角三角尺如图11①所示放置,图②是由图①抽象出的几何图形,点B,C,E在同一条直线上,连接DC.
(1)请找出图②中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母);
(2)求证:DC⊥BE.
图11
16.(12分)如图12,在△ABC中,AD平分∠BAC,DG⊥BC于点G,DE⊥AB于点E,DF⊥AC交其延长线于点F,BE=CF.
求证:BG=CG.
图12
17.(12分)如图13,在△ABC中,AB=AC,点M在△ABC内,AM平分∠BAC,点D与点M在AC所在直线的两侧,AD⊥AB,AD=BC,点E在AC边上,CE=AM,连接MD,BE.
(1)依题意补全图形.
(2)请判断MD与BE的数量关系,并进行证明.
(3)点M在何处时,BM+BE会有最小值,画出图形确定点M的位置;如果AB=5,BC=6,求出BM+BE的最小值.
图13
答案
1.B 2.D 3.C 4.D 5.C 6.D 7.C
8.三角形的稳定性
9.40° 10.(2)(3)
11.1
13.a+c+5b 2a+16b
14.解:(1)补全图形如图.
(2)证明:∵AB⊥AC,BE⊥AD,CF⊥AD,
∴∠BAE+∠CAF=90°,∠BAE+∠B=90°,∠CFA=∠AEB=90°.
∴∠CAF=∠B.
在△ABE和△CAF中,
∴△ABE≌△CAF(AAS).
∴BE=AF,AE=CF.
∵AF=AE+EF,
∴BE=EF+CF.
15.解:(1)△BAE≌△CAD.
证明如下:
∵∠BAC=∠DAE=90°,
∴∠BAE=∠CAD.
又∵AB=AC,AE=AD,
∴△BAE≌△CAD.
(2)证明:∵△BAE≌△CAD,
∴∠BEA=∠CDA.
又∵∠ADE=45°,
∴∠BEA+∠CDE=45°.
又∵∠DEA=45°,
∴∠CDE+∠DEC=90°.
∴∠BCD=90°,
即DC⊥BE.
16.证明:连接BD,CD.
∵AD平分∠BAC,DE⊥AB于点E,DF⊥AC交其延长线于点F,
∴DE=DF.
在△DEB和△DFC中,
∴△DEB≌△DFC.
∴DB=DC.
又∵DG⊥BC,
∴BG=CG.
17.解:(1)补全图形如图①.
(2)MD=BE.
证明:延长AM交BC于点F,如图②.
∵AM平分∠BAC,
∴∠BAM=∠CAM.
∵AD⊥AB,∴∠MAD+∠BAM=90°.
∴∠MAD+∠CAM=90°.
∵AB=AC,AM平分∠BAC,∴AF⊥BC.
∴∠C+∠CAM=90°.
∴∠MAD=∠C.
又∵AM=CE,AD=BC,
∴△AMD≌△CEB.
∴MD=BE.
(3)由(2)可知,BM+BE=BM+MD,根据两点之间线段最短,连接BD,BD与AM所在直线的交点即为点M的位置,如图③所示.
∵AD=BC,BC=6,
∴AD=BC=6.
∴在Rt△ABD中,BD===.
∴BM+BE的最小值为.
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
