2021—2022学年湘教版八年级数学上册第2章三角形单元测试题(word版含答案)
文档属性
| 名称 | 2021—2022学年湘教版八年级数学上册第2章三角形单元测试题(word版含答案) | 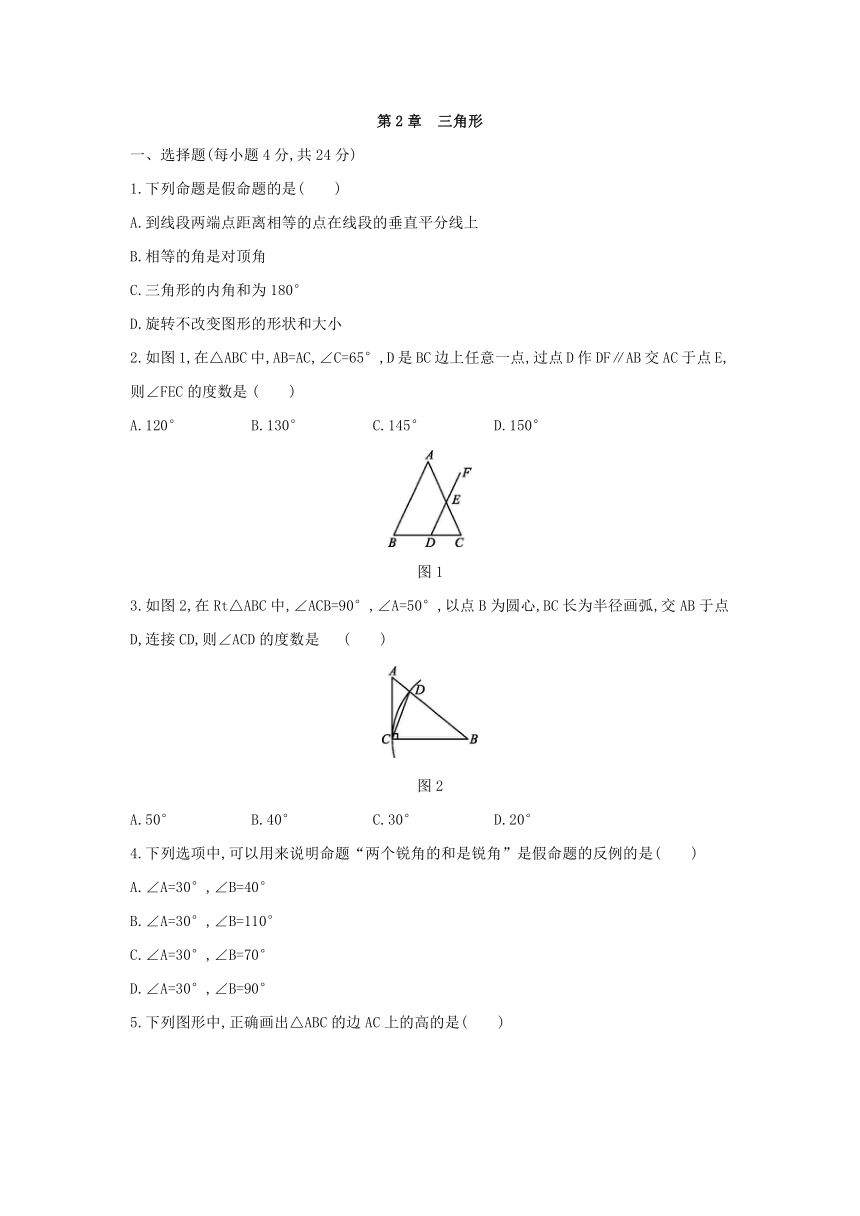 | |
| 格式 | zip | ||
| 文件大小 | 149.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-30 20:08:29 | ||
图片预览


文档简介
第2章 三角形
一、选择题(每小题4分,共24分)
1.下列命题是假命题的是( )
A.到线段两端点距离相等的点在线段的垂直平分线上
B.相等的角是对顶角
C.三角形的内角和为180°
D.旋转不改变图形的形状和大小
2.如图1,在△ABC中,AB=AC,∠C=65°,D是BC边上任意一点,过点D作DF∥AB交AC于点E,则∠FEC的度数是
( )
A.120°
B.130°
C.145°
D.150°
图1
3.如图2,在Rt△ABC中,∠ACB=90°,∠A=50°,以点B为圆心,BC长为半径画弧,交AB于点D,连接CD,则∠ACD的度数是
( )
图2
A.50°
B.40°
C.30°
D.20°
4.下列选项中,可以用来说明命题“两个锐角的和是锐角”是假命题的反例的是( )
A.∠A=30°,∠B=40°
B.∠A=30°,∠B=110°
C.∠A=30°,∠B=70°
D.∠A=30°,∠B=90°
5.下列图形中,正确画出△ABC的边AC上的高的是( )
图3
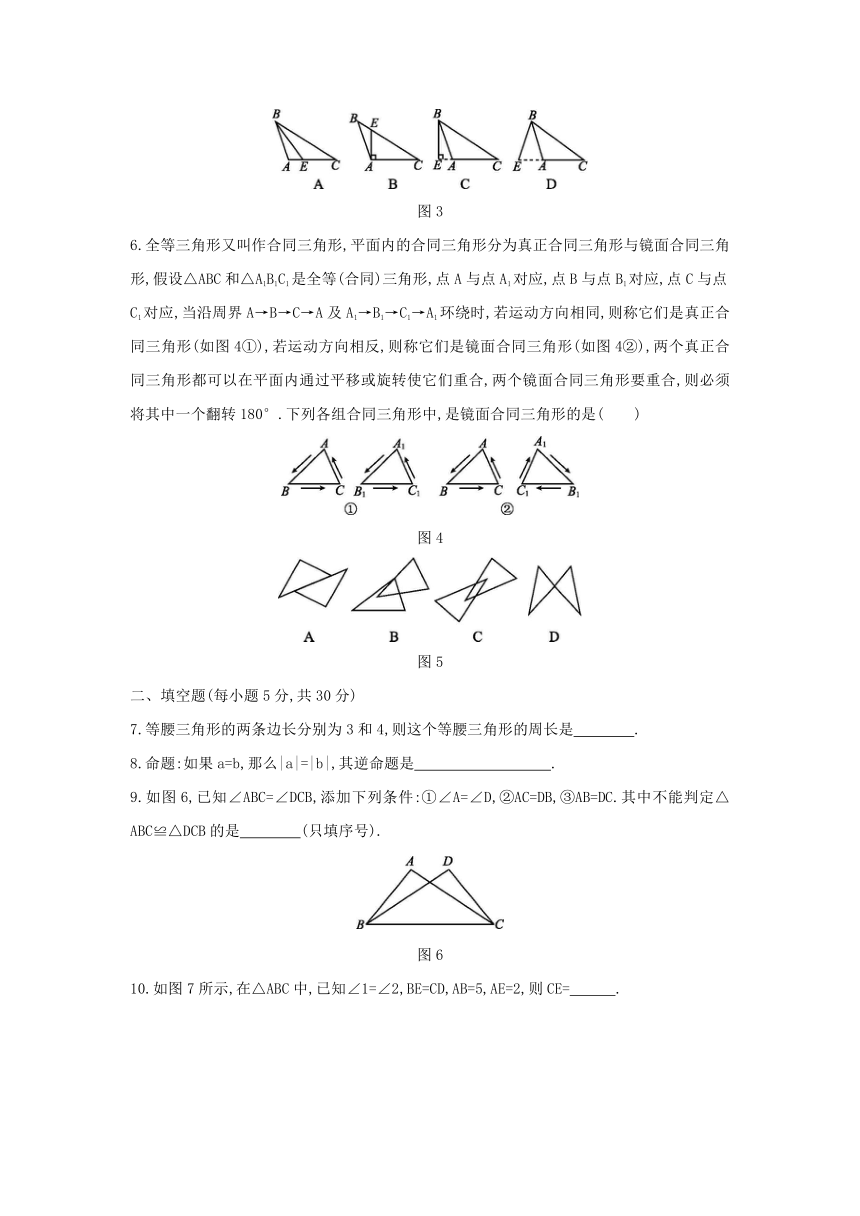
6.全等三角形又叫作合同三角形,平面内的合同三角形分为真正合同三角形与镜面合同三角形,假设△ABC和△A1B1C1是全等(合同)三角形,点A与点A1对应,点B与点B1对应,点C与点C1对应,当沿周界A→B→C→A及A1→B1→C1→A1环绕时,若运动方向相同,则称它们是真正合同三角形(如图4①),若运动方向相反,则称它们是镜面合同三角形(如图4②),两个真正合同三角形都可以在平面内通过平移或旋转使它们重合,两个镜面合同三角形要重合,则必须将其中一个翻转180°.下列各组合同三角形中,是镜面合同三角形的是( )
图4
图5
二、填空题(每小题5分,共30分)
7.等腰三角形的两条边长分别为3和4,则这个等腰三角形的周长是 .?
8.命题:如果a=b,那么|a|=|b|,其逆命题是 .?
9.如图6,已知∠ABC=∠DCB,添加下列条件:①∠A=∠D,②AC=DB,③AB=DC.其中不能判定△ABC≌△DCB的是 (只填序号).?
图6
10.如图7所示,在△ABC中,已知∠1=∠2,BE=CD,AB=5,AE=2,则CE= .?
图7
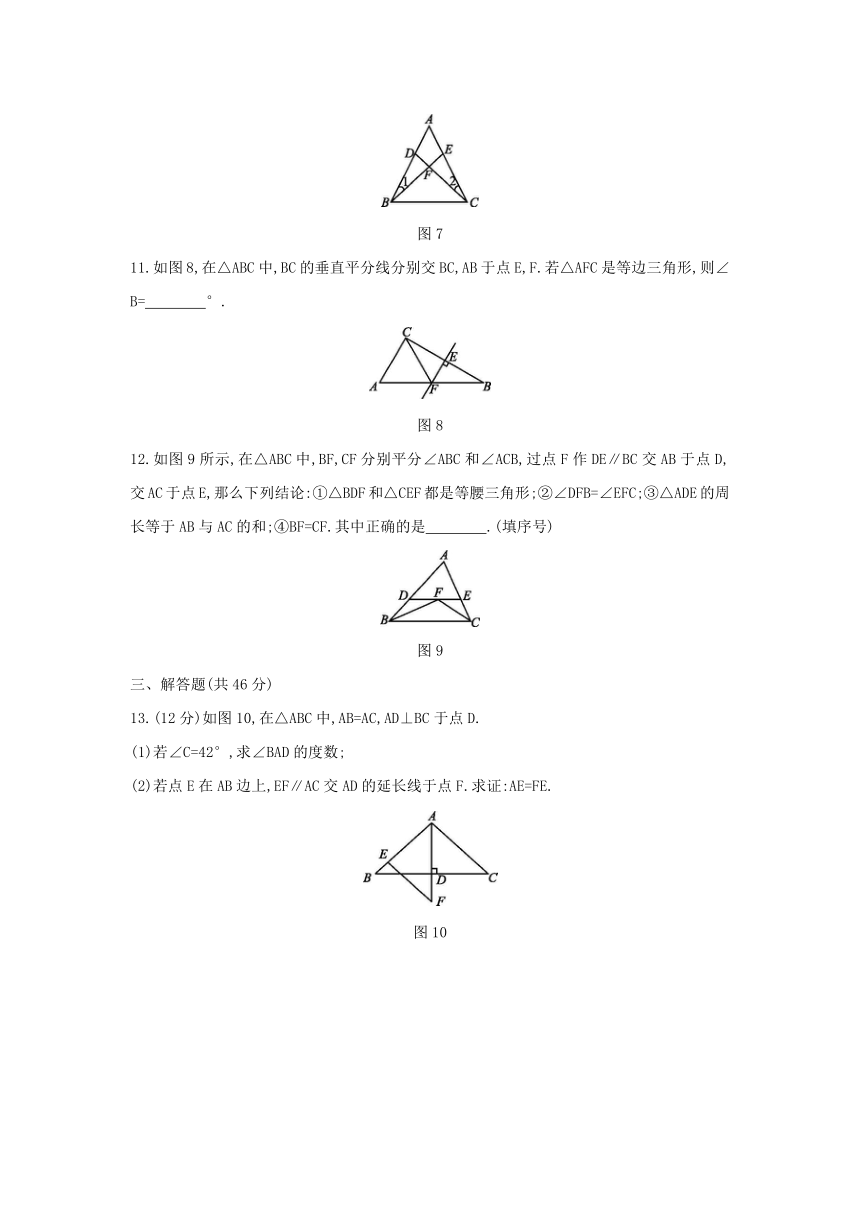
11.如图8,在△ABC中,BC的垂直平分线分别交BC,AB于点E,F.若△AFC是等边三角形,则∠B= °.?
图8
12.如图9所示,在△ABC中,BF,CF分别平分∠ABC和∠ACB,过点F作DE∥BC交AB于点D,交AC于点E,那么下列结论:①△BDF和△CEF都是等腰三角形;②∠DFB=∠EFC;③△ADE的周长等于AB与AC的和;④BF=CF.其中正确的是 .(填序号)?
图9
三、解答题(共46分)
13.(12分)如图10,在△ABC中,AB=AC,AD⊥BC于点D.
(1)若∠C=42°,求∠BAD的度数;
(2)若点E在AB边上,EF∥AC交AD的延长线于点F.求证:AE=FE.
图10
14.(12分)如图11,在△ABC中,AB=AC,点E,F在边BC上,BE=CF,点D在AF的延长线上,AD=AC.
(1)求证:△ABE≌△ACF;
(2)若∠BAE=30°,求∠ADC的度数.
图11
15.(10分)如图12所示,在△ABC中,AB=BC,点D在AB的延长线上.
(1)利用尺规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法).
①作∠CBD的平分线BM;
②作边BC上的中线AE,并延长AE交BM于点F.
图12
(2)由(1)得BF与边AC的位置关系是 .?
16.(12分)问题:如图13,在△ABD中,BA=BD.在BD的延长线上取点E,C,作△AEC,使EA=EC,若∠BAE=90°,∠B=45°,求∠DAC的度数.
答案:∠DAC=45°.
思考:(1)如果把以上“问题”中的条件“∠B=45°”去掉,其余条件不变,那么∠DAC的度数会改变吗?请说明理由;
(2)如果把以上“问题”中的条件“∠B=45°”去掉,再将“∠BAE=90°”改为“∠BAE=n°”,其余条件不变,求∠DAC的度数.
图13
答案
1.B
2.B [解析]
∵AB=AC,∴∠B=∠C=65°.
∵DF∥AB,∴∠EDC=∠B=65°,∴∠FEC=∠EDC+∠C=65°+65°=130°.
3.D [解析]
∵在Rt△ABC中,∠ACB=90°,∠A=50°,∴∠B=40°.∵BC=BD,∴∠BCD=∠BDC=(180°-40°)=70°,∴∠ACD=90°-70°=20°.故选D.
4.C
5.C
6.D
7.10或11 [解析]
①当3是腰长时,三角形的三边长分别为3,3,4,此时能组成三角形,所以周长=3+3+4=10;②当3是底边长时,三角形的三边分别为3,4,4,此时能组成三角形,所以周长=3+4+4=11.综上所述,这个等腰三角形的周长是10或11.
8.如果|a|=|b|,那么a=b [解析]
对于两个命题,如果一个命题的条件和结论分别是另外一个命题的结论和条件,那么这两个命题叫作互逆命题,其中一个命题叫作原命题,另外一个命题叫作原命题的逆命题.
9.② [解析]
已知∠ABC=∠DCB,题图中有公共边BC=CB,因而添加①∠A=∠D可用AAS证明全等,添加③可用SAS证明全等,添加②就变成了“SSA”,不能判定全等.
10.3
11.30 [解析]
∵FE垂直平分BC,∴FC=FB,
∴∠B=∠BCF.∵△ACF是等边三角形,
∴∠AFC=60°,∴∠B=30°.
12.①③ [解析]
①∵DE∥BC,∴∠DFB=∠FBC,∠EFC=∠FCB.∵BF是∠ABC的平分线,CF是∠ACB的平分线,∴∠FBC=∠DBF,∠FCE=∠FCB,∴∠DBF=∠DFB,∠EFC=∠ECF,则△BDF,△CEF都是等腰三角形.∴①正确;②∵△ABC不是等腰三角形,∴∠DFB=∠EFC是错误的;③∵△BDF,△CEF都是等腰三角形,∴DF=DB,FE=EC,即有DE=DF+FE=DB+EC,∴△ADE的周长=AD+AE+DE=AD+AE+DB+EC=AB+AC.∴③正确;④∵△ABC不是等腰三角形,∴∠ABC≠∠ACB,∴∠FBC≠∠FCB,
∴BF=CF是错误的.
故答案为①③.
13.解:(1)∵AB=AC,∠C=42°,∴∠B=∠C=42°,∴∠BAC=180°-∠B-∠C=180°-42°-42°=96°.∵AD⊥BC,∴∠BAD=∠BAC=×96°=48°.
(2)证明:∵EF∥AC,∴∠CAF=∠F.
∵AB=AC,AD⊥BC,∴∠CAF=∠EAF,
∴∠F=∠EAF,∴AE=FE.
14.解:(1)证明:∵AB=AC,
∴∠B=∠ACF.
在△ABE和△ACF中,
∴△ABE≌△ACF.
(2)由(1)知△ABE≌△ACF,
∴∠CAF=∠BAE=30°.
又∵AD=AC,
∴∠ADC=∠ACD==75°.
15.解:(1)①如图所示,BM即所求.
②如图所示,AF即所求.
(2)BF∥AC
16.解:(1)∠DAC的度数不会改变.理由如下:
∵EA=EC,∴∠CAE=∠C,①
∴∠AED=2∠C.
∵∠BAE=90°,BA=BD,
∴∠BAD=[180°-(90°-2∠C)]=45°+∠C,
∴∠DAE=90°-∠BAD=90°-(45°+∠C)=45°-∠C.②
由①②,得∠DAC=∠DAE+∠CAE=45°.
(2)设∠ABC=m°,则∠BAD=(180°-m°)=90°-m°,∠AEB=180°-n°-m°,
∴∠DAE=n°-∠BAD=n°-90°+m°.
∵EA=EC,
∴∠CAE=∠AEB=90°-n°-m°,
∴∠DAC=∠DAE+∠CAE=n°-90°+m°+90°-n°-m°=n°.
一、选择题(每小题4分,共24分)
1.下列命题是假命题的是( )
A.到线段两端点距离相等的点在线段的垂直平分线上
B.相等的角是对顶角
C.三角形的内角和为180°
D.旋转不改变图形的形状和大小
2.如图1,在△ABC中,AB=AC,∠C=65°,D是BC边上任意一点,过点D作DF∥AB交AC于点E,则∠FEC的度数是
( )
A.120°
B.130°
C.145°
D.150°
图1
3.如图2,在Rt△ABC中,∠ACB=90°,∠A=50°,以点B为圆心,BC长为半径画弧,交AB于点D,连接CD,则∠ACD的度数是
( )
图2
A.50°
B.40°
C.30°
D.20°
4.下列选项中,可以用来说明命题“两个锐角的和是锐角”是假命题的反例的是( )
A.∠A=30°,∠B=40°
B.∠A=30°,∠B=110°
C.∠A=30°,∠B=70°
D.∠A=30°,∠B=90°
5.下列图形中,正确画出△ABC的边AC上的高的是( )
图3
6.全等三角形又叫作合同三角形,平面内的合同三角形分为真正合同三角形与镜面合同三角形,假设△ABC和△A1B1C1是全等(合同)三角形,点A与点A1对应,点B与点B1对应,点C与点C1对应,当沿周界A→B→C→A及A1→B1→C1→A1环绕时,若运动方向相同,则称它们是真正合同三角形(如图4①),若运动方向相反,则称它们是镜面合同三角形(如图4②),两个真正合同三角形都可以在平面内通过平移或旋转使它们重合,两个镜面合同三角形要重合,则必须将其中一个翻转180°.下列各组合同三角形中,是镜面合同三角形的是( )
图4
图5
二、填空题(每小题5分,共30分)
7.等腰三角形的两条边长分别为3和4,则这个等腰三角形的周长是 .?
8.命题:如果a=b,那么|a|=|b|,其逆命题是 .?
9.如图6,已知∠ABC=∠DCB,添加下列条件:①∠A=∠D,②AC=DB,③AB=DC.其中不能判定△ABC≌△DCB的是 (只填序号).?
图6
10.如图7所示,在△ABC中,已知∠1=∠2,BE=CD,AB=5,AE=2,则CE= .?
图7
11.如图8,在△ABC中,BC的垂直平分线分别交BC,AB于点E,F.若△AFC是等边三角形,则∠B= °.?
图8
12.如图9所示,在△ABC中,BF,CF分别平分∠ABC和∠ACB,过点F作DE∥BC交AB于点D,交AC于点E,那么下列结论:①△BDF和△CEF都是等腰三角形;②∠DFB=∠EFC;③△ADE的周长等于AB与AC的和;④BF=CF.其中正确的是 .(填序号)?
图9
三、解答题(共46分)
13.(12分)如图10,在△ABC中,AB=AC,AD⊥BC于点D.
(1)若∠C=42°,求∠BAD的度数;
(2)若点E在AB边上,EF∥AC交AD的延长线于点F.求证:AE=FE.
图10
14.(12分)如图11,在△ABC中,AB=AC,点E,F在边BC上,BE=CF,点D在AF的延长线上,AD=AC.
(1)求证:△ABE≌△ACF;
(2)若∠BAE=30°,求∠ADC的度数.
图11
15.(10分)如图12所示,在△ABC中,AB=BC,点D在AB的延长线上.
(1)利用尺规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法).
①作∠CBD的平分线BM;
②作边BC上的中线AE,并延长AE交BM于点F.
图12
(2)由(1)得BF与边AC的位置关系是 .?
16.(12分)问题:如图13,在△ABD中,BA=BD.在BD的延长线上取点E,C,作△AEC,使EA=EC,若∠BAE=90°,∠B=45°,求∠DAC的度数.
答案:∠DAC=45°.
思考:(1)如果把以上“问题”中的条件“∠B=45°”去掉,其余条件不变,那么∠DAC的度数会改变吗?请说明理由;
(2)如果把以上“问题”中的条件“∠B=45°”去掉,再将“∠BAE=90°”改为“∠BAE=n°”,其余条件不变,求∠DAC的度数.
图13
答案
1.B
2.B [解析]
∵AB=AC,∴∠B=∠C=65°.
∵DF∥AB,∴∠EDC=∠B=65°,∴∠FEC=∠EDC+∠C=65°+65°=130°.
3.D [解析]
∵在Rt△ABC中,∠ACB=90°,∠A=50°,∴∠B=40°.∵BC=BD,∴∠BCD=∠BDC=(180°-40°)=70°,∴∠ACD=90°-70°=20°.故选D.
4.C
5.C
6.D
7.10或11 [解析]
①当3是腰长时,三角形的三边长分别为3,3,4,此时能组成三角形,所以周长=3+3+4=10;②当3是底边长时,三角形的三边分别为3,4,4,此时能组成三角形,所以周长=3+4+4=11.综上所述,这个等腰三角形的周长是10或11.
8.如果|a|=|b|,那么a=b [解析]
对于两个命题,如果一个命题的条件和结论分别是另外一个命题的结论和条件,那么这两个命题叫作互逆命题,其中一个命题叫作原命题,另外一个命题叫作原命题的逆命题.
9.② [解析]
已知∠ABC=∠DCB,题图中有公共边BC=CB,因而添加①∠A=∠D可用AAS证明全等,添加③可用SAS证明全等,添加②就变成了“SSA”,不能判定全等.
10.3
11.30 [解析]
∵FE垂直平分BC,∴FC=FB,
∴∠B=∠BCF.∵△ACF是等边三角形,
∴∠AFC=60°,∴∠B=30°.
12.①③ [解析]
①∵DE∥BC,∴∠DFB=∠FBC,∠EFC=∠FCB.∵BF是∠ABC的平分线,CF是∠ACB的平分线,∴∠FBC=∠DBF,∠FCE=∠FCB,∴∠DBF=∠DFB,∠EFC=∠ECF,则△BDF,△CEF都是等腰三角形.∴①正确;②∵△ABC不是等腰三角形,∴∠DFB=∠EFC是错误的;③∵△BDF,△CEF都是等腰三角形,∴DF=DB,FE=EC,即有DE=DF+FE=DB+EC,∴△ADE的周长=AD+AE+DE=AD+AE+DB+EC=AB+AC.∴③正确;④∵△ABC不是等腰三角形,∴∠ABC≠∠ACB,∴∠FBC≠∠FCB,
∴BF=CF是错误的.
故答案为①③.
13.解:(1)∵AB=AC,∠C=42°,∴∠B=∠C=42°,∴∠BAC=180°-∠B-∠C=180°-42°-42°=96°.∵AD⊥BC,∴∠BAD=∠BAC=×96°=48°.
(2)证明:∵EF∥AC,∴∠CAF=∠F.
∵AB=AC,AD⊥BC,∴∠CAF=∠EAF,
∴∠F=∠EAF,∴AE=FE.
14.解:(1)证明:∵AB=AC,
∴∠B=∠ACF.
在△ABE和△ACF中,
∴△ABE≌△ACF.
(2)由(1)知△ABE≌△ACF,
∴∠CAF=∠BAE=30°.
又∵AD=AC,
∴∠ADC=∠ACD==75°.
15.解:(1)①如图所示,BM即所求.
②如图所示,AF即所求.
(2)BF∥AC
16.解:(1)∠DAC的度数不会改变.理由如下:
∵EA=EC,∴∠CAE=∠C,①
∴∠AED=2∠C.
∵∠BAE=90°,BA=BD,
∴∠BAD=[180°-(90°-2∠C)]=45°+∠C,
∴∠DAE=90°-∠BAD=90°-(45°+∠C)=45°-∠C.②
由①②,得∠DAC=∠DAE+∠CAE=45°.
(2)设∠ABC=m°,则∠BAD=(180°-m°)=90°-m°,∠AEB=180°-n°-m°,
∴∠DAE=n°-∠BAD=n°-90°+m°.
∵EA=EC,
∴∠CAE=∠AEB=90°-n°-m°,
∴∠DAC=∠DAE+∠CAE=n°-90°+m°+90°-n°-m°=n°.
同课章节目录
