2021—2022学年京改版数学九年级上册 第二十二章圆(下) 单元测试题(含答案)
文档属性
| 名称 | 2021—2022学年京改版数学九年级上册 第二十二章圆(下) 单元测试题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 225.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-30 21:05:50 | ||
图片预览



文档简介
第二十二章 圆(下)
一、选择题(每题5分,共40分)
1.已知直线l与☉O相交,若☉O的半径为3,则点O到直线l的距离d的取值范围是
( )
A.0≤d<3
B.d<3
C.d=3
D.d>3
2.如图1,PA,PB是☉O的切线,A,B为切点,AC是☉O的直径,若∠P=40°,则∠BAC的度数为
( )
图1
A.40°
B.80°
C.20°
D.10°
3.半径相等的圆内接正三角形、正方形、正六边形的边长之比为
( )
A.1∶∶
B.∶∶1
C.3∶2∶1
D.1∶2∶3
4.图2为4×4的正方形网格图,A,B,C,D,O均在格点上,点O是
( )
图2
A.△ACD的外心
B.△ABC的外心
C.△ACD的内心
D.△ABC的内心
5.如图3,已知☉O的半径为1,圆心O到直线l的距离为2,过l上任一点A作☉O的切线,切点为B,则线段AB长度的最小值为
( )
图3
A.1
B.
C.
D.2
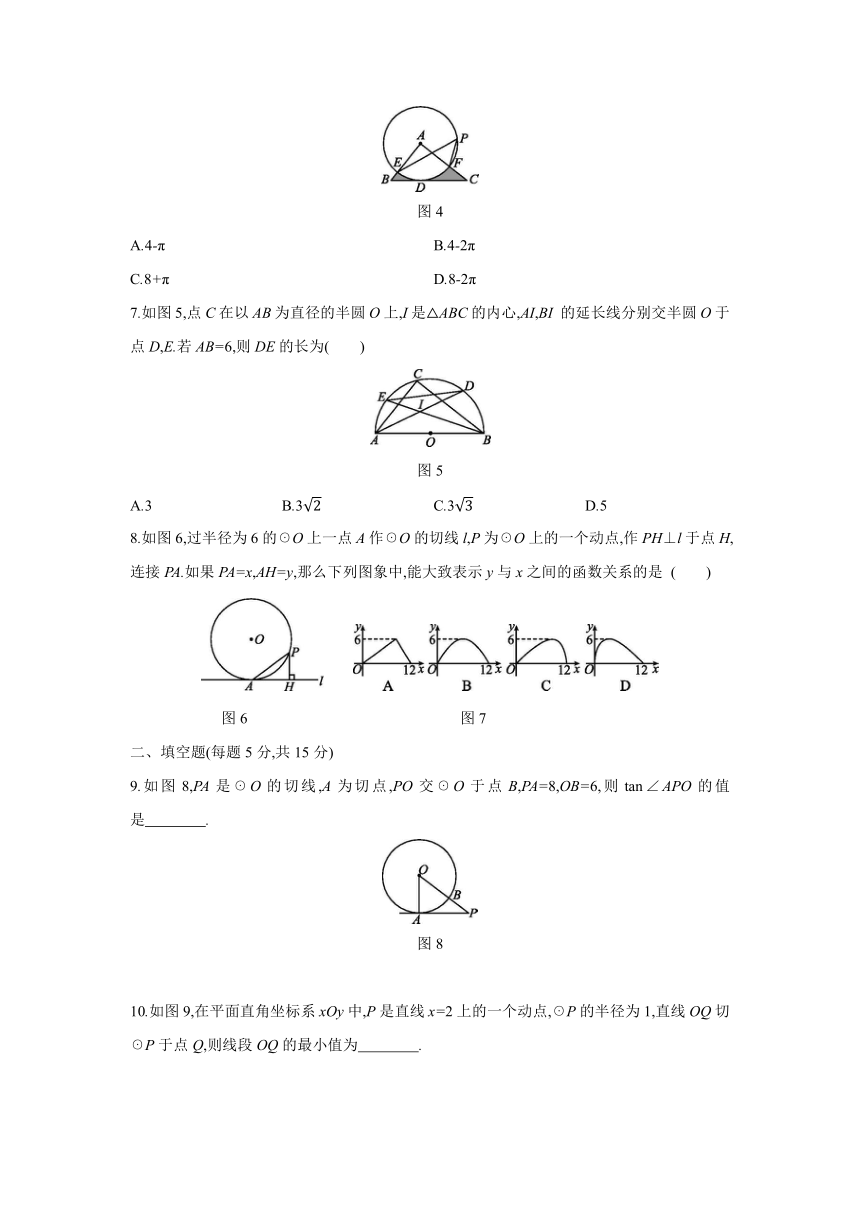
6.如图4,在△ABC中,BC=4,以点A为圆心,2为半径的☉A与BC相切于点D,交AB于点E,交AC于点F,P是☉A上的一点,且∠EPF=45°,则图中阴影部分的面积为
( )
图4
A.4-π
B.4-2π
C.8+π
D.8-2π
7.如图5,点C在以AB为直径的半圆O上,I是△ABC的内心,AI,BI
的延长线分别交半圆O于点D,E.若AB=6,则DE的长为( )
图5
A.3
B.3
C.3
D.5
8.如图6,过半径为6的☉O上一点A作☉O的切线l,P为☉O上的一个动点,作PH⊥l于点H,连接PA.如果PA=x,AH=y,那么下列图象中,能大致表示y与x之间的函数关系的是
( )
图6
图7
二、填空题(每题5分,共15分)
9.如图8,PA是☉O的切线,A为切点,PO交☉O于点B,PA=8,OB=6,则tan∠APO的值是 .?
图8
10.如图9,在平面直角坐标系xOy中,P是直线x=2上的一个动点,☉P的半径为1,直线OQ切☉P于点Q,则线段OQ的最小值为 .?
图9
11.我们知道任意三角形都存在内切圆.同样的,一些凸四边形也存在内切圆.我们规定:存在与凸四边形的三条边相切的圆叫四边形的伪内切圆.以下结论正确的是 .(填序号)?
①凸四边形必存在伪内切圆;
②当平行四边形只存在1个伪内切圆时,它的对角线一定相等;
③矩形伪内切圆的个数可能为1,2,4;
④当且仅当四边形的对角线互相垂直平分且相等时,该四边形的伪内切圆与内切圆重合.
三、解答题(共45分)
12.(15分)如图10,AB为☉O的直径,C为☉O上一点,☉O的切线BD交OC的延长线于点D.
(1)求证:∠DBC=∠OCA;
(2)若∠BAC=30°,AC=2,求CD的长.
图10
13.(15分)如图11,O为∠ABC的边BC上的一点,过点O作OM⊥AB于点M,到点O的距离等于线段OM的长的所有点组成图形W.图形W与射线BC交于E,F两点(点E在点F的左侧).
(1)过点M作MH⊥BC于点H,如果BE=2,sin∠ABC=,求MH的长;
(2)将射线BC绕点B顺时针旋转得到射线BD,使得∠CBD+∠MOB=90°,判断射线BD与图形W公共点的个数,并证明.
图11
14.(15分)如图12,AB是☉O的直径,C,D是☉O上两点,且=,连接OC,BD,OD.
(1)求证:OC垂直平分BD.
(2)过点C作☉O的切线交AB的延长线于点E,连接AD,CD.
①依题意补全图形;
②若AD=6,sin∠AEC=,求CD的长.
图12
答案
1.A 2.C
3.B [解析]
设圆的半径为R,圆内接正三角形、正方形、正六边形的边长分别为a3,a4,a6,
则正三角形的边心距为R,
边长a3=2=R;
正方形中a4=R;正六边形中a6=R,
所以a3∶a4∶a6=R∶R∶R=∶∶1.
4.B
5.C [解析]
如图①所示,连接OB.
∵AB是☉O的切线,∴OB⊥AB.
在Rt△AOB中,
AB==,
∴只有当OA取最小值时,AB才最小,
∴当OA⊥直线l时,OA最小,如图②,此时AB===.故选C.
6.A [解析]
连接AD,则AD⊥BC,且AD=2,所以S△ABC=BC·AD=×4×2=4.又因为∠EPF=45°,所以∠EAF=90°,所以S扇形AEF==π,因此图中阴影部分的面积为4-π.
7.B [解析]
连接OD,OE.
∵I是△ABC的内心,
∴∠CAB=2∠DAB,∠ABC=2∠ABE.
∵点C在以AB为直径的半圆O上,
∴∠C=90°,
∴∠CAB+∠ABC=90°,
∴2∠DAB+2∠ABE=90°.
∵∠DOB=2∠DAB,∠AOE=2∠ABE,
∴∠DOB+∠AOE=90°,
∴∠DOE=180°-(∠DOB+∠AOE)=90°.
∵OD=OE=AB=3,
∴DE==3.故选B.
8.C
9. [解析]
∵PA是☉O的切线,A为切点,
∴∠OAP=90°,则tan∠APO===.
10. [解析]
连接OP,PQ,如图.
∵直线OQ切☉P于点Q,∴PQ⊥OQ.
在Rt△POQ中,OQ=.
∵P是直线x=2上的一个动点,
∴OP的最小值为2,
∴OQ的最小值为=.
11.① [解析]
①正确.如图(a)所示,四边形ABCD必存在伪内切圆.
②错误.菱形是平行四边形,只存在一个伪内切圆,对角线不相等.如图(b)所示.
③错误.矩形伪内切圆的个数可能为1,4,如图(c)所示.
④错误.当且仅当四边形的对角线互相垂直平分且相等时,这个四边形是正方形,它的伪内切圆与内切圆重合,菱形也符合条件,故结论错误.
故答案为①.
12.解:(1)证明:∵BD是☉O的切线,
∴∠OBD=∠OBC+∠DBC=90°.
∵AB是☉O的直径,
∴∠ACB=∠OCA+∠OCB=90°.
∵OC=OB,∴∠OBC=∠OCB,
∴∠DBC=∠OCA.
(2)在Rt△ACB中,∠A=30°,AC=2,
可得CB=ACtan
A=
.
∵∠A=30°,∴∠COB=2∠A=60°,
∴∠D=90°-∠COB=30°.
∵OA=OC,∴∠OCA=∠A=30°,
∴∠DBC=∠OCA=30°,
∴∠D=∠DBC,
∴CB=CD,∴CD=
.
13.解:(1)∵到点O的距离等于线段OM的长的所有点组成图形W,
∴图形W是以点O为圆心,OM的长为半径的圆.
根据题意补全图形如图①.
∵OM⊥AB于点M,
∴∠BMO=90°.
在△BMO中,sin∠ABC==,
∴BO=OM.
∵BE=2,∴BO=2+OE=OM,
解得OM=OE=4,∴BO=6.
在Rt△BOM中,
BM2+OM2=BO2,∴BM=2.
S△BMO=OM·MB=MH·BO,
解得MH=
.
(2)射线BD与图形W的公共点个数为1个.
证明:如图②,过点O作ON⊥BD于点N.
由题易知图形W是以点O为圆心,OM长为半径的圆.
∵∠CBD+∠MOB=90°,
且∠ABC+∠MOB=90°,
∴∠CBD=∠ABC,
∴OM=ON,
∴BD为☉O的切线,
∴射线BD与图形W的公共点个数为1个.
14.解:(1)证明:∵=,
∴∠COD=∠COB.
∵OD=OB,∴OC垂直平分BD.
(2)①补全图形,如图所示.
②∵CE是☉O的切线,切点为C,
∴OC⊥CE于点C.
如图,记OC与BD交于点F,由(1)可知OC⊥BD,
∴∠OCE=∠OFB=90°,∴BD∥CE,
∴∠AEC=∠ABD.
在Rt△ABD中,AD=6,sin∠AEC=sin∠ABD=,
∴BD=8,AB=10,∴OA=OB=OC=5.
由(1)可知OC平分BD,即DF=BF,
∴BF=DF=4,OF为△ABD的中位线,
∴OF=AD=3,∴CF=2.
在Rt△CFD中,CD==2.
故CD的长为2.
一、选择题(每题5分,共40分)
1.已知直线l与☉O相交,若☉O的半径为3,则点O到直线l的距离d的取值范围是
( )
A.0≤d<3
B.d<3
C.d=3
D.d>3
2.如图1,PA,PB是☉O的切线,A,B为切点,AC是☉O的直径,若∠P=40°,则∠BAC的度数为
( )
图1
A.40°
B.80°
C.20°
D.10°
3.半径相等的圆内接正三角形、正方形、正六边形的边长之比为
( )
A.1∶∶
B.∶∶1
C.3∶2∶1
D.1∶2∶3
4.图2为4×4的正方形网格图,A,B,C,D,O均在格点上,点O是
( )
图2
A.△ACD的外心
B.△ABC的外心
C.△ACD的内心
D.△ABC的内心
5.如图3,已知☉O的半径为1,圆心O到直线l的距离为2,过l上任一点A作☉O的切线,切点为B,则线段AB长度的最小值为
( )
图3
A.1
B.
C.
D.2
6.如图4,在△ABC中,BC=4,以点A为圆心,2为半径的☉A与BC相切于点D,交AB于点E,交AC于点F,P是☉A上的一点,且∠EPF=45°,则图中阴影部分的面积为
( )
图4
A.4-π
B.4-2π
C.8+π
D.8-2π
7.如图5,点C在以AB为直径的半圆O上,I是△ABC的内心,AI,BI
的延长线分别交半圆O于点D,E.若AB=6,则DE的长为( )
图5
A.3
B.3
C.3
D.5
8.如图6,过半径为6的☉O上一点A作☉O的切线l,P为☉O上的一个动点,作PH⊥l于点H,连接PA.如果PA=x,AH=y,那么下列图象中,能大致表示y与x之间的函数关系的是
( )
图6
图7
二、填空题(每题5分,共15分)
9.如图8,PA是☉O的切线,A为切点,PO交☉O于点B,PA=8,OB=6,则tan∠APO的值是 .?
图8
10.如图9,在平面直角坐标系xOy中,P是直线x=2上的一个动点,☉P的半径为1,直线OQ切☉P于点Q,则线段OQ的最小值为 .?
图9
11.我们知道任意三角形都存在内切圆.同样的,一些凸四边形也存在内切圆.我们规定:存在与凸四边形的三条边相切的圆叫四边形的伪内切圆.以下结论正确的是 .(填序号)?
①凸四边形必存在伪内切圆;
②当平行四边形只存在1个伪内切圆时,它的对角线一定相等;
③矩形伪内切圆的个数可能为1,2,4;
④当且仅当四边形的对角线互相垂直平分且相等时,该四边形的伪内切圆与内切圆重合.
三、解答题(共45分)
12.(15分)如图10,AB为☉O的直径,C为☉O上一点,☉O的切线BD交OC的延长线于点D.
(1)求证:∠DBC=∠OCA;
(2)若∠BAC=30°,AC=2,求CD的长.
图10
13.(15分)如图11,O为∠ABC的边BC上的一点,过点O作OM⊥AB于点M,到点O的距离等于线段OM的长的所有点组成图形W.图形W与射线BC交于E,F两点(点E在点F的左侧).
(1)过点M作MH⊥BC于点H,如果BE=2,sin∠ABC=,求MH的长;
(2)将射线BC绕点B顺时针旋转得到射线BD,使得∠CBD+∠MOB=90°,判断射线BD与图形W公共点的个数,并证明.
图11
14.(15分)如图12,AB是☉O的直径,C,D是☉O上两点,且=,连接OC,BD,OD.
(1)求证:OC垂直平分BD.
(2)过点C作☉O的切线交AB的延长线于点E,连接AD,CD.
①依题意补全图形;
②若AD=6,sin∠AEC=,求CD的长.
图12
答案
1.A 2.C
3.B [解析]
设圆的半径为R,圆内接正三角形、正方形、正六边形的边长分别为a3,a4,a6,
则正三角形的边心距为R,
边长a3=2=R;
正方形中a4=R;正六边形中a6=R,
所以a3∶a4∶a6=R∶R∶R=∶∶1.
4.B
5.C [解析]
如图①所示,连接OB.
∵AB是☉O的切线,∴OB⊥AB.
在Rt△AOB中,
AB==,
∴只有当OA取最小值时,AB才最小,
∴当OA⊥直线l时,OA最小,如图②,此时AB===.故选C.
6.A [解析]
连接AD,则AD⊥BC,且AD=2,所以S△ABC=BC·AD=×4×2=4.又因为∠EPF=45°,所以∠EAF=90°,所以S扇形AEF==π,因此图中阴影部分的面积为4-π.
7.B [解析]
连接OD,OE.
∵I是△ABC的内心,
∴∠CAB=2∠DAB,∠ABC=2∠ABE.
∵点C在以AB为直径的半圆O上,
∴∠C=90°,
∴∠CAB+∠ABC=90°,
∴2∠DAB+2∠ABE=90°.
∵∠DOB=2∠DAB,∠AOE=2∠ABE,
∴∠DOB+∠AOE=90°,
∴∠DOE=180°-(∠DOB+∠AOE)=90°.
∵OD=OE=AB=3,
∴DE==3.故选B.
8.C
9. [解析]
∵PA是☉O的切线,A为切点,
∴∠OAP=90°,则tan∠APO===.
10. [解析]
连接OP,PQ,如图.
∵直线OQ切☉P于点Q,∴PQ⊥OQ.
在Rt△POQ中,OQ=.
∵P是直线x=2上的一个动点,
∴OP的最小值为2,
∴OQ的最小值为=.
11.① [解析]
①正确.如图(a)所示,四边形ABCD必存在伪内切圆.
②错误.菱形是平行四边形,只存在一个伪内切圆,对角线不相等.如图(b)所示.
③错误.矩形伪内切圆的个数可能为1,4,如图(c)所示.
④错误.当且仅当四边形的对角线互相垂直平分且相等时,这个四边形是正方形,它的伪内切圆与内切圆重合,菱形也符合条件,故结论错误.
故答案为①.
12.解:(1)证明:∵BD是☉O的切线,
∴∠OBD=∠OBC+∠DBC=90°.
∵AB是☉O的直径,
∴∠ACB=∠OCA+∠OCB=90°.
∵OC=OB,∴∠OBC=∠OCB,
∴∠DBC=∠OCA.
(2)在Rt△ACB中,∠A=30°,AC=2,
可得CB=ACtan
A=
.
∵∠A=30°,∴∠COB=2∠A=60°,
∴∠D=90°-∠COB=30°.
∵OA=OC,∴∠OCA=∠A=30°,
∴∠DBC=∠OCA=30°,
∴∠D=∠DBC,
∴CB=CD,∴CD=
.
13.解:(1)∵到点O的距离等于线段OM的长的所有点组成图形W,
∴图形W是以点O为圆心,OM的长为半径的圆.
根据题意补全图形如图①.
∵OM⊥AB于点M,
∴∠BMO=90°.
在△BMO中,sin∠ABC==,
∴BO=OM.
∵BE=2,∴BO=2+OE=OM,
解得OM=OE=4,∴BO=6.
在Rt△BOM中,
BM2+OM2=BO2,∴BM=2.
S△BMO=OM·MB=MH·BO,
解得MH=
.
(2)射线BD与图形W的公共点个数为1个.
证明:如图②,过点O作ON⊥BD于点N.
由题易知图形W是以点O为圆心,OM长为半径的圆.
∵∠CBD+∠MOB=90°,
且∠ABC+∠MOB=90°,
∴∠CBD=∠ABC,
∴OM=ON,
∴BD为☉O的切线,
∴射线BD与图形W的公共点个数为1个.
14.解:(1)证明:∵=,
∴∠COD=∠COB.
∵OD=OB,∴OC垂直平分BD.
(2)①补全图形,如图所示.
②∵CE是☉O的切线,切点为C,
∴OC⊥CE于点C.
如图,记OC与BD交于点F,由(1)可知OC⊥BD,
∴∠OCE=∠OFB=90°,∴BD∥CE,
∴∠AEC=∠ABD.
在Rt△ABD中,AD=6,sin∠AEC=sin∠ABD=,
∴BD=8,AB=10,∴OA=OB=OC=5.
由(1)可知OC平分BD,即DF=BF,
∴BF=DF=4,OF为△ABD的中位线,
∴OF=AD=3,∴CF=2.
在Rt△CFD中,CD==2.
故CD的长为2.
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
