12.4.2回归直线_教案1-湘教版数学必修5
文档属性
| 名称 | 12.4.2回归直线_教案1-湘教版数学必修5 |

|
|
| 格式 | doc | ||
| 文件大小 | 86.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-29 00:00:00 | ||
图片预览

文档简介
回归直线
【教学目标】
1. 了解相关关系、回归分析、散点图、回归直线方程的概念.
2. 掌握散点图的画法,掌握回归直线方程的求解方法,会求回归直线方程.
3. 让学生参与回归直线的探求,结合身边的实例,发现散点图的线性特征,主动构建线性回归直线方程的模型.
【教学重点】
散点图的画法,回归直线方程的求解方法.
【教学难点】
回归直线方程的求解方法.
【教学方法】
这节课主要采取启发引导和讲练结合的方法.通过创设情境、设置问题等手段对学生进行了启发、诱导,结合讨论法、讲授法组织学生自主探究.然后结合例题及课后练习巩固求回归直线方程的步骤.
【教学过程】
环节 教学内容 师生互动 设计意图
导入 1.请说出正方形面积S与边长x之间的关系.
正方形边长x 面积:S = x2
2.人的身高不能确定体重,但平均说来“身高者,体也重”.那么身高和体重具有什么关系?
身高和体重之间具有不确定的关系.
3.类似的情况生活中还有:
(1)商品销售收入与广告支出经费;
(2)粮食产量与施肥量. 教师引导学生得出结论:两个变量之间除了函数关系外还有相关关系. 通过生活实例认识现实生活中存在大量的非确定性的相关关系.
新
课
新
课
新
课 1. 相关关系与函数关系的异同点
相关关系
函数关系
相同点
均是指两个变量的关系
不同点
非确定的关系
确定的关系
两个随机变量的关系
两个非随机变量的关系
2.一元回归分析
通常把研究两个变量间的相关关系叫做一元回归分析.
看下面的例子.
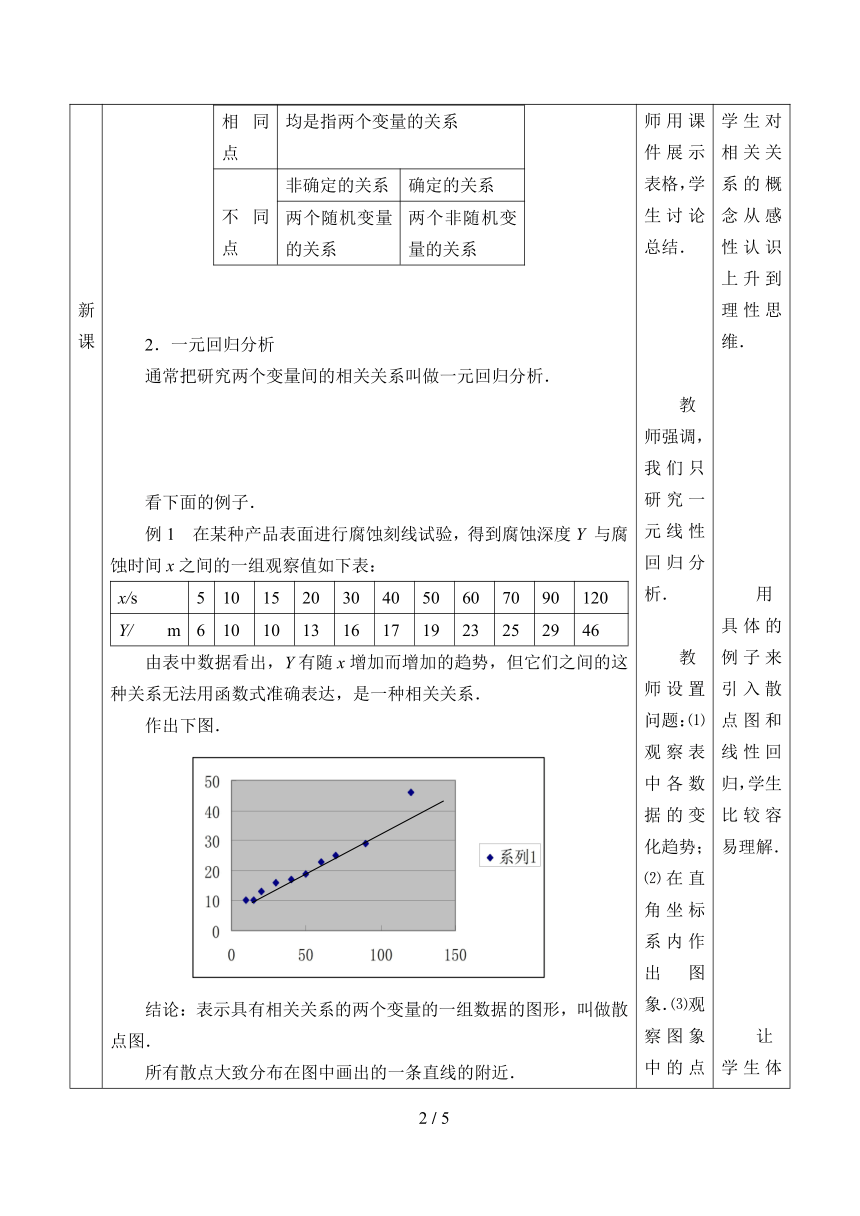
例1 在某种产品表面进行腐蚀刻线试验,得到腐蚀深度Y 与腐蚀时间x之间的一组观察值如下表:
x/s
5
10
15
20
30
40
50
60
70
90
120
Y/iim
6
10
10
13
16
17
19
23
25
29
46
由表中数据看出,Y有随x增加而增加的趋势,但它们之间的这种关系无法用函数式准确表达,是一种相关关系.
作出下图.
结论:表示具有相关关系的两个变量的一组数据的图形,叫做散点图.
所有散点大致分布在图中画出的一条直线的附近.
显然这样的直线还可以画出许多条,而我们希望找出其中的一条,它能最好地反映x与Y之间的关系,这条直线就叫回归直线,记此直线方程为
=a+bx. ①
则①式叫做Y对x的回归方程,b叫做回归系数.而且
②
下面列用公式②来求例1中,腐蚀深度Y对腐蚀时间x的回归直线方程.
序号
x
y
x2
y2
xy
1
5
6
25
36
30
2
10
10
100
100
100
3
15
10
225
100
150
4
20
13
400
169
260
5
30
16
900
256
480
6
40
17
1 600
289
680
7
50
19
2 500
361
950
8
60
53
3 600
529
1 380
9
70
25
4 900
625
1 750
10
90
29
8 100
841
2 610
11
120
46
1 400
2 116
5 520
∑
510
214
36 750
5 422
13 910
由上表算得,x平均数为 ,y的平均数为 ,代入公式②得
b≈0.304 336,a≈5.34.
即所求回归直线方程为
=0.034x+5.34.
这里回归系数b=0.304的意义是:腐蚀时间x每增加一个单位,深度Y平均增加0.304个单位.
例2 设对变量x,Y有如下观察数据:
x
151
152
153
154
156
157
158
160
160
162
163
164
Y
40
41
41
41.5
42
42.5
43
44
45
45
46
45.5
使用函数型计算器求Y对x的回归直线方程.(结果保留到小数点后三位数字)
解:按教材P193页所示步骤可得
a≈-27.759,b≈0.450.
所以Y对x的回归直线方程为
=0.450x+27.759.
特别指出:
应用回归直线方程可以把非确定性问题转化成确定性问题,把“无序”变为“有序”,并对情况进行估测、补充.因此,学过回归直线方程以后,应用回归直线方程可解决相关的实际问题.
教师用课件展示表格,学生讨论总结.
教师强调,我们只研究一元线性回归分析.
教师设置问题:⑴观察表中各数据的变化趋势;⑵在直角坐标系内作出图象.⑶观察图象中的点有什么特点?
学生解答.
教师指导学生用excel作图.
教师问如何才能确定回归直线方程.
学生回答,只要确定a与回归系数b.
学生记忆公式.
教师列出表格.
学生完成计算.
教师指导学生使用计算器求回归直线方程.
教师给出总结,帮助学生构建新知识.
让学生对相关关系的概念从感性认识上升到理性思维.
用具体的例子来引入散点图和线性回归,学生比较容易理解.
让学生体验信息技术在数学学习中的乐趣.
公式的推导较复杂,故让学生直接记忆.
让学生在计算过程中树立严谨的科学态度.
通过例2体现使用计算器处理的优越性.使学生认识学习回归直线方程的意义.
小 结 求回归直线方程的步骤:
⑴计算平均数;
⑵计算的积,求;
⑶计算;
⑷将结果代入公式求b;
⑸用 求a;
⑹写出回归方程. 教师引导学生一起回顾求回归直线方程的步骤.
6 / 6
【教学目标】
1. 了解相关关系、回归分析、散点图、回归直线方程的概念.
2. 掌握散点图的画法,掌握回归直线方程的求解方法,会求回归直线方程.
3. 让学生参与回归直线的探求,结合身边的实例,发现散点图的线性特征,主动构建线性回归直线方程的模型.
【教学重点】
散点图的画法,回归直线方程的求解方法.
【教学难点】
回归直线方程的求解方法.
【教学方法】
这节课主要采取启发引导和讲练结合的方法.通过创设情境、设置问题等手段对学生进行了启发、诱导,结合讨论法、讲授法组织学生自主探究.然后结合例题及课后练习巩固求回归直线方程的步骤.
【教学过程】
环节 教学内容 师生互动 设计意图
导入 1.请说出正方形面积S与边长x之间的关系.
正方形边长x 面积:S = x2
2.人的身高不能确定体重,但平均说来“身高者,体也重”.那么身高和体重具有什么关系?
身高和体重之间具有不确定的关系.
3.类似的情况生活中还有:
(1)商品销售收入与广告支出经费;
(2)粮食产量与施肥量. 教师引导学生得出结论:两个变量之间除了函数关系外还有相关关系. 通过生活实例认识现实生活中存在大量的非确定性的相关关系.
新
课
新
课
新
课 1. 相关关系与函数关系的异同点
相关关系
函数关系
相同点
均是指两个变量的关系
不同点
非确定的关系
确定的关系
两个随机变量的关系
两个非随机变量的关系
2.一元回归分析
通常把研究两个变量间的相关关系叫做一元回归分析.
看下面的例子.
例1 在某种产品表面进行腐蚀刻线试验,得到腐蚀深度Y 与腐蚀时间x之间的一组观察值如下表:
x/s
5
10
15
20
30
40
50
60
70
90
120
Y/iim
6
10
10
13
16
17
19
23
25
29
46
由表中数据看出,Y有随x增加而增加的趋势,但它们之间的这种关系无法用函数式准确表达,是一种相关关系.
作出下图.
结论:表示具有相关关系的两个变量的一组数据的图形,叫做散点图.
所有散点大致分布在图中画出的一条直线的附近.
显然这样的直线还可以画出许多条,而我们希望找出其中的一条,它能最好地反映x与Y之间的关系,这条直线就叫回归直线,记此直线方程为
=a+bx. ①
则①式叫做Y对x的回归方程,b叫做回归系数.而且
②
下面列用公式②来求例1中,腐蚀深度Y对腐蚀时间x的回归直线方程.
序号
x
y
x2
y2
xy
1
5
6
25
36
30
2
10
10
100
100
100
3
15
10
225
100
150
4
20
13
400
169
260
5
30
16
900
256
480
6
40
17
1 600
289
680
7
50
19
2 500
361
950
8
60
53
3 600
529
1 380
9
70
25
4 900
625
1 750
10
90
29
8 100
841
2 610
11
120
46
1 400
2 116
5 520
∑
510
214
36 750
5 422
13 910
由上表算得,x平均数为 ,y的平均数为 ,代入公式②得
b≈0.304 336,a≈5.34.
即所求回归直线方程为
=0.034x+5.34.
这里回归系数b=0.304的意义是:腐蚀时间x每增加一个单位,深度Y平均增加0.304个单位.
例2 设对变量x,Y有如下观察数据:
x
151
152
153
154
156
157
158
160
160
162
163
164
Y
40
41
41
41.5
42
42.5
43
44
45
45
46
45.5
使用函数型计算器求Y对x的回归直线方程.(结果保留到小数点后三位数字)
解:按教材P193页所示步骤可得
a≈-27.759,b≈0.450.
所以Y对x的回归直线方程为
=0.450x+27.759.
特别指出:
应用回归直线方程可以把非确定性问题转化成确定性问题,把“无序”变为“有序”,并对情况进行估测、补充.因此,学过回归直线方程以后,应用回归直线方程可解决相关的实际问题.
教师用课件展示表格,学生讨论总结.
教师强调,我们只研究一元线性回归分析.
教师设置问题:⑴观察表中各数据的变化趋势;⑵在直角坐标系内作出图象.⑶观察图象中的点有什么特点?
学生解答.
教师指导学生用excel作图.
教师问如何才能确定回归直线方程.
学生回答,只要确定a与回归系数b.
学生记忆公式.
教师列出表格.
学生完成计算.
教师指导学生使用计算器求回归直线方程.
教师给出总结,帮助学生构建新知识.
让学生对相关关系的概念从感性认识上升到理性思维.
用具体的例子来引入散点图和线性回归,学生比较容易理解.
让学生体验信息技术在数学学习中的乐趣.
公式的推导较复杂,故让学生直接记忆.
让学生在计算过程中树立严谨的科学态度.
通过例2体现使用计算器处理的优越性.使学生认识学习回归直线方程的意义.
小 结 求回归直线方程的步骤:
⑴计算平均数;
⑵计算的积,求;
⑶计算;
⑷将结果代入公式求b;
⑸用 求a;
⑹写出回归方程. 教师引导学生一起回顾求回归直线方程的步骤.
6 / 6
同课章节目录
