湖北省安陆一中2012届高三数学第十次综合试题(文科)
文档属性
| 名称 | 湖北省安陆一中2012届高三数学第十次综合试题(文科) |  | |
| 格式 | zip | ||
| 文件大小 | 252.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-23 19:03:03 | ||
图片预览

文档简介
2012届高三数学第十次综合试题(文科)
参考公式
(1),其中,
(2)方差,其中为,,…,的平均数
(3)
0.15 0.10 0.05 0.025 0.010 0.005 0.001
2.072 2.706 3.841 5.024 6.635 7.879 10.828
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.若是夹角为的两个单位向量,则
A.-4 B.-3 C. D.-7
2.设集合,,则“”是“”的
A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件 D.既不充分也不必要条件
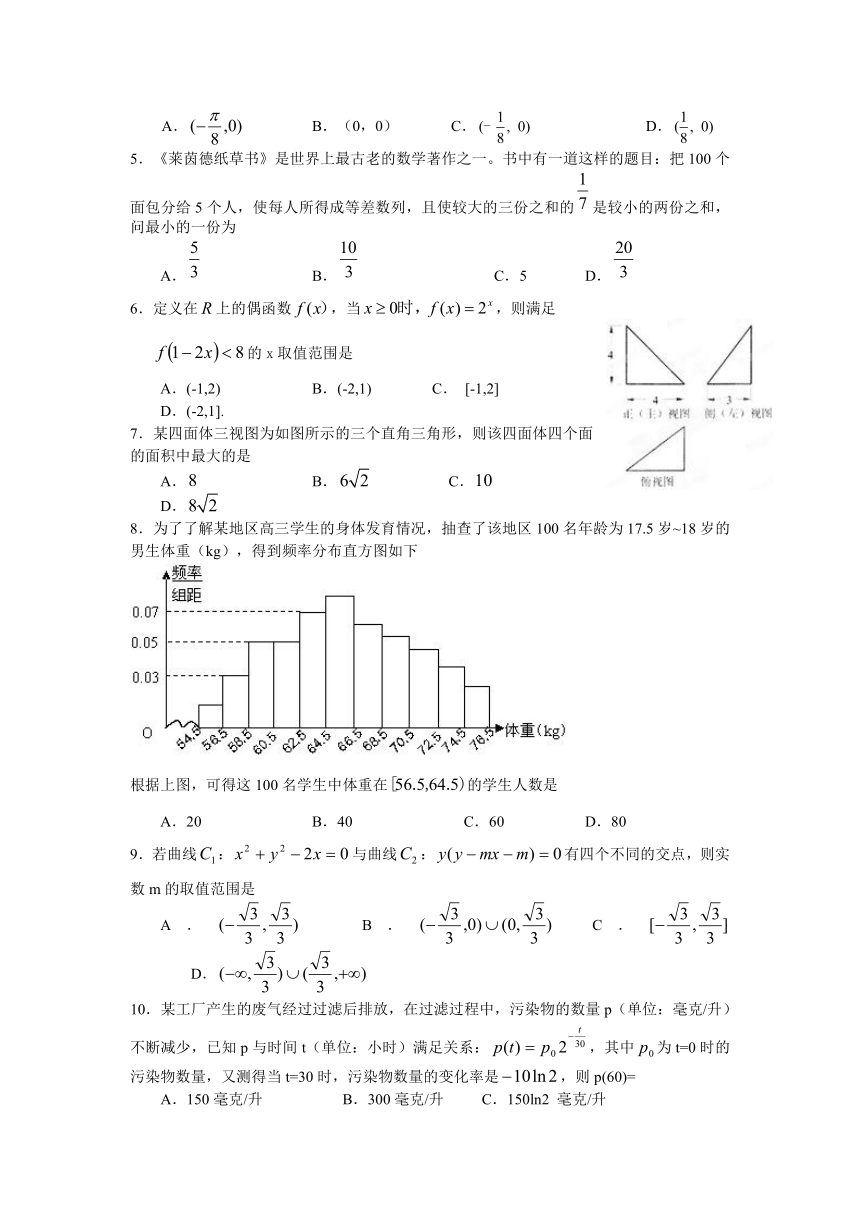
3.如图给出的是计算的值的一个程序框图,其中判断框内应填入的条件是( )
A. B. C. D.
4.若函数的最小正周期为1,则它的图象的一个对称中心为
A. B.(0,0) C. D.
5.《莱茵德纸草书》是世界上最古老的数学著作之一。书中有一道这样的题目:把100个面包分给5个人,使每人所得成等差数列,且使较大的三份之和的是较小的两份之和,问最小的一份为
A. B. C.5 D.
6.定义在上的偶函数,当,则满足的x取值范围是
A.(-1,2) B.(-2,1) C. [-1,2] D.(-2,1].
7.某四面体三视图为如图所示的三个直角三角形,则该四面体四个面的面积中最大的是
A. B. C. D.
8.为了了解某地区高三学生的身体发育情况,抽查了该地区100名年龄为17.5岁~18岁的男生体重(kg),得到频率分布直方图如下
根据上图,可得这100名学生中体重在的学生人数是
A.20 B.40 C.60 D.80
9.若曲线:与曲线:有四个不同的交点,则实数m的取值范围是
A. B. C. D.
10.某工厂产生的废气经过过滤后排放,在过滤过程中,污染物的数量p(单位:毫克/升)不断减少,已知p与时间t(单位:小时)满足关系:,其中为t=0时的污染物数量,又测得当t=30时,污染物数量的变化率是,则p(60)=
A.150毫克/升 B.300毫克/升 C.150ln2 毫克/升 D.300ln2毫克/升
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题:本大题共7小题,每小题5分,共35分.请将答案填在答题卡中相应的位置
11.复数
12.已知线性回归方程
13.某班数学兴趣小组有男生和女生各3名,现从中任选2名学生去参加校数学竞赛,则
至少有一名参赛学生是男生的概率为
14.已知,则的取值范围是
15.中a、b、c分别为内角A、B、C所对的边,且则BC边上的高等于
16.已知曲线C的方程为,则当C为双曲线时,的取值范围是 当C为焦点在轴上的椭圆时,的取值范围是
17.已知且则h的最大值等于
三、解答题:本大题共6个小题,共75分.解答应写出文字说明,证明过程或演算步骤
18.(本题满分12分):设函数(I)对的图像作如下变换:先将的图像向右平移个单位,再将横坐标伸长到原来的2倍,纵坐标不变,得到函数的图像,求的解析式;(II)已知,且,求的值。
19.(本题满分12分)如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,点E在线段AD上,CE∥AB。(Ⅰ)求证:CE⊥平面PAD;(Ⅱ)若PA=AB=1,AD=3,且CD与平面PAD所成的角为45°,求点D到平面PCE的距离。
20.(本题满分13分)已知数列中,且 (),又设。(Ⅰ)求数列的通项及前n项和;(Ⅱ)假设对任意n>1都有,求 的取值范围。
21.(本题满分14分).已知三次函数的导函数,,,为实数。
(I)若曲线在点(,)处切线的斜率为12,求的值;(II)若在区间上的最小值、最大值分别为和1,且,求函数的解析式。
22.(本题满分14分)已知在直角坐标平面XOY中,有一个不在Y轴上的动点P(x,y),到定点F(0,)的距离比它到X轴的距离多,记P点的轨迹为曲线C(I)求曲线C的方程;(II)已知点M在Y轴上,且过点F的直线与曲线C交于A、B两点,若 为正三角形,求M点的坐标与直线的方程。
2012届高三数学第十次综合试题(文科)答案
选择题:
CCACA ACBBA
填空题:
11. ;12.4;13. ;14. ;15. ;16. ,;17. ;
解答题:
18.(1);(2);
19.(2);
20.(1);(2);
21.(1);(2)
22.(1);(2)或,;
参考公式
(1),其中,
(2)方差,其中为,,…,的平均数
(3)
0.15 0.10 0.05 0.025 0.010 0.005 0.001
2.072 2.706 3.841 5.024 6.635 7.879 10.828
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.若是夹角为的两个单位向量,则
A.-4 B.-3 C. D.-7
2.设集合,,则“”是“”的
A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件 D.既不充分也不必要条件
3.如图给出的是计算的值的一个程序框图,其中判断框内应填入的条件是( )
A. B. C. D.
4.若函数的最小正周期为1,则它的图象的一个对称中心为
A. B.(0,0) C. D.
5.《莱茵德纸草书》是世界上最古老的数学著作之一。书中有一道这样的题目:把100个面包分给5个人,使每人所得成等差数列,且使较大的三份之和的是较小的两份之和,问最小的一份为
A. B. C.5 D.
6.定义在上的偶函数,当,则满足的x取值范围是
A.(-1,2) B.(-2,1) C. [-1,2] D.(-2,1].
7.某四面体三视图为如图所示的三个直角三角形,则该四面体四个面的面积中最大的是
A. B. C. D.
8.为了了解某地区高三学生的身体发育情况,抽查了该地区100名年龄为17.5岁~18岁的男生体重(kg),得到频率分布直方图如下
根据上图,可得这100名学生中体重在的学生人数是
A.20 B.40 C.60 D.80
9.若曲线:与曲线:有四个不同的交点,则实数m的取值范围是
A. B. C. D.
10.某工厂产生的废气经过过滤后排放,在过滤过程中,污染物的数量p(单位:毫克/升)不断减少,已知p与时间t(单位:小时)满足关系:,其中为t=0时的污染物数量,又测得当t=30时,污染物数量的变化率是,则p(60)=
A.150毫克/升 B.300毫克/升 C.150ln2 毫克/升 D.300ln2毫克/升
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题:本大题共7小题,每小题5分,共35分.请将答案填在答题卡中相应的位置
11.复数
12.已知线性回归方程
13.某班数学兴趣小组有男生和女生各3名,现从中任选2名学生去参加校数学竞赛,则
至少有一名参赛学生是男生的概率为
14.已知,则的取值范围是
15.中a、b、c分别为内角A、B、C所对的边,且则BC边上的高等于
16.已知曲线C的方程为,则当C为双曲线时,的取值范围是 当C为焦点在轴上的椭圆时,的取值范围是
17.已知且则h的最大值等于
三、解答题:本大题共6个小题,共75分.解答应写出文字说明,证明过程或演算步骤
18.(本题满分12分):设函数(I)对的图像作如下变换:先将的图像向右平移个单位,再将横坐标伸长到原来的2倍,纵坐标不变,得到函数的图像,求的解析式;(II)已知,且,求的值。
19.(本题满分12分)如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,点E在线段AD上,CE∥AB。(Ⅰ)求证:CE⊥平面PAD;(Ⅱ)若PA=AB=1,AD=3,且CD与平面PAD所成的角为45°,求点D到平面PCE的距离。
20.(本题满分13分)已知数列中,且 (),又设。(Ⅰ)求数列的通项及前n项和;(Ⅱ)假设对任意n>1都有,求 的取值范围。
21.(本题满分14分).已知三次函数的导函数,,,为实数。
(I)若曲线在点(,)处切线的斜率为12,求的值;(II)若在区间上的最小值、最大值分别为和1,且,求函数的解析式。
22.(本题满分14分)已知在直角坐标平面XOY中,有一个不在Y轴上的动点P(x,y),到定点F(0,)的距离比它到X轴的距离多,记P点的轨迹为曲线C(I)求曲线C的方程;(II)已知点M在Y轴上,且过点F的直线与曲线C交于A、B两点,若 为正三角形,求M点的坐标与直线的方程。
2012届高三数学第十次综合试题(文科)答案
选择题:
CCACA ACBBA
填空题:
11. ;12.4;13. ;14. ;15. ;16. ,;17. ;
解答题:
18.(1);(2);
19.(2);
20.(1);(2);
21.(1);(2)
22.(1);(2)或,;
同课章节目录
