人教新课标版七下调查统计(3)一案三单设计
文档属性
| 名称 | 人教新课标版七下调查统计(3)一案三单设计 |

|
|
| 格式 | zip | ||
| 文件大小 | 76.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-23 19:07:48 | ||
图片预览




文档简介
调查统计(2)教学设计
【教材地位分析】
本节是在学习了前两节简单随机抽样和系统抽样的基础上,结合此两种随机抽样特点和适用范围,针对总体的复杂性,为提高样本的代表性,有学习掌握分层抽样这种随机抽样的必要性;为下节“用样本估计总体”的学习打下了基础.因此本节内容具有承前启后的作用,地位重要.
【重点、难点】
重点:正确理解分层抽样的定义,灵活应用分层抽样抽取样本,并恰当的选择三种抽样方法解决现实生活中的抽样问题。
难点:恰当的选择三种抽样方法解决现实生活中的抽样问题。
【教学目标】
知识与技能目标:
(1)正确理解分层抽样的概念;
(2)掌握分层抽样的一般步骤;
(3)区分简单随机抽样、系统抽样和分层抽样,并选择适当正确的方法进行抽样。 过程与方法目标:
通过对现实生活中实际问题进行分层抽样,感知应用数学知识解决实际问题的方法。感悟有具体到一般的研究方法,培养学生的归纳概括能力。
情感与态度目标:
通过对统计学知识的研究,感知数学知识中“估计”与“精确”性的矛盾统一,培养学生的辩证唯物主义的世界观与价值观。
【学生分析】
⑴知识掌握上,虽然学生已经掌握了数据的收集、整理、描述的一些方法,但还很不熟练,尤其扇形统计图的画法和描述,学生掌握很困难,所以有必要作好复习 。
⑵学生学习本节课的知识障碍。对于抽样调查和全面调查的特征学生在观察和归纳方面说的不准确,所以教学中教师应做好示范,适当提示,让学生根据实际情况采取恰当的调查方法;在选取样本时机会可能不均等,提醒学生选取的样本要具有代表性。
【教学方法】
引导学生课前用好《问题导读---评价单》,对所学知识进行提前预习,找出难理解的问题,以便上课更有针对性。
结合本节课的教学内容和学生的认知水平,在教法上,我采用“启发—探究—讨论”式教学模式,充分发挥教师的主导作用,让学生真正成为教学活动的主体。授课过程中注意导学生充分利用《问题生成---评价单》。
然后辅之《问题训练---评价单》进行课堂知识的巩固和验证。
【教师课前准备】
《问题导读---评价单》、《问题生成---评价单》、《问题训练---评价单》
【教学过程设计】
问题与情境 师生行为 设计意图
(一)学前准备,创设情境从上节课我们已经看到在总体数目比较大时,对它进行全面调查很难做到,甚至根本就不可能,如:某地区有百万电视观众,要想了解他们对新闻、体育、动画、娱乐、戏曲五类节目的喜爱情况,能否像上节课中提到的抽100名学生来估计2000名学生的喜爱情况吗?(二)探求新知上述情况显然不能。由于学生、成年人、老年人各自喜爱的节目不一样,所以要了解整个地区的观众的情况,需要在更大范围内抽取样本。由于在各个年龄段对节目的爱好有明显的不同,而同一个年龄段对节目的爱好往往存在共性,所以可以对青少年、成年人、老年人各段人群分别进行简单随机抽样,即分层次抽样,使每个年龄段都能抽取一定的人数来代表所在的人群,然后汇总调查结果。1、那么如何按层次抽取呢?2、那么如何统计出各段人数对节目的喜爱的百分比呢?这个表格又如何设计呢? 三、知识拓展下表是用分层抽样进行调查并整理得到的数据。请你自己画条形统计图和扇形统计图描述上表中的数据。1、从上表中可以大致估计整个地区观众对四种节目的喜爱情况,你能谈谈吗?2、还可以估计各个年龄段中观众对某类节目喜爱的情况。能根据上表中的数据进行估计吗?为什么?3、那么根据什么来进行估计呢?4、从表中你看到了什么?5、不同年龄段的观众对节目喜爱不尽相同。用什么方式可以直观地反映这种变化呢?折线统计图。四、接受考验发放《问题训练---评价单》,学生独立完成上面的练习题五.反思回顾1.通过本课的学习,你学到了哪些新的知识?2.在学习这些知识的过程中,你的经验与教训是什么? 让学生利用课前问题导读评价单进行充分大预习,找出有难点的问题,以增强上课的听课效果。可以按年龄段的实际人口的比例分配来确保每个年龄段都有相应的比例的代表,教材中按青少年、成年人、老年人的人数比为2:5:3抽取请同学们计算按这样的比例各段分别应抽取多少人,并列出表格。青少年成年人老年人合计抽取人数2005003001000在抽取的1000名观众中,对各类节目的喜爱情况整理、绘制成喜爱节目的人数统计表:青少年成年人老年人合计百分比A新闻1112510323923.90%B体育471146322422.40%C动画55531812612.60%D娱乐741765930930.90%E戏曲13325710210.20%合计2005003001000100%先将总体分成几个年龄段(层),然后再在各年龄段(层)中进行简单随机抽样,这是一种分层抽样。分层抽取的样本与这个地区所有观众的年龄结构基本相同,与在整个地区直接进行简单随机抽样相比,更具有代表性。青少年成年人老年人新闻25%34.5%体育23.5%22.8%21%……………………青少年成年人老年人合计百分比A新闻1112510323923.90%B体育471146322422.40%C动画55531812612.60%D娱乐741765930930.90%E戏曲13325710210.20%合计2005003001000100%例如,估计各个年龄段中观众对动画类节目和娱乐类节目喜爱的情况。不能。因为不同年龄层抽取的人数不相等。可根据不同年龄层中喜爱动画和娱乐类节目的百分比来估计。青少年成年人老年人动画28%11.2%9.3%娱乐39%37.6%23.3%下图是不同年龄段观众喜爱娱乐和动画类节目的折线统计图。 从上图中可以清楚地看到,随着年龄的增加,观众对动画类、娱乐类的喜爱程度逐渐下降。 设计意图:实际生活中的问题导入,带给学生轻松愉快的心情,从而也引出了本节课的课题。设计意图:教师提出问题,学生合作讨论,这种教学方法可以让学生体会知识的形成过程,从而加深对知识的理解和运用通过学生合作讨论完成样本的抽取,表格的整理及图形的绘制,使学生体会了知识的形成过程,便于学生理解和记忆。设计意图:通过学生对自己整理的数据的分析,培养了学生数学知识服务员生活的思想 设设计意图:让学灵活运用,加强对知识的理解,题目设计了不同层次的练习题,这样也能使不同水平的学生得到最大程度的发展设计意图:这样可以培养学生归纳总结能力和语言表达能力
调查统计(3)教学设计
设计者: 班级: 姓名:
【教学目标】
知识与技能目标:
(1)正确理解分层抽样的概念;
(2)掌握分层抽样的一般步骤;
(3)区分简单随机抽样、系统抽样和分层抽样,并选择适当正确的方法进行抽样。 过程与方法目标:
通过对现实生活中实际问题进行分层抽样,感知应用数学知识解决实际问题的方法。感悟有具体到一般的研究方法,培养学生的归纳概括能力。
情感与态度目标:
通过对统计学知识的研究,感知数学知识中“估计”与“精确”性的矛盾统一,培养学生的辩证唯物主义的世界观与价值观。
为你导航
1、在扇形统计图中,有两个扇形的圆心角度数之比为3∶4,且较小扇形表示24本课本书,则较大扇形表示________本课本书.
2、如图,某校四个年级男女生人数的条形统计图,则学生最多的年级是 .
3、据统计,某班50名学生参加2011年初中毕业生学业考试,综合评价等级为A,B,C等的学生情况如扇形图所示,则该班得A等的学生有______名.
4、某班50名学生右眼视力的检查结果如下表:
视力 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 1.0 1.2 1.5
人数 1 1 3 4 3 4 4 6 8 10 6
(1)视力为1.5的有_____人,视力为1.0的有______人,视力小于1.0的有______人.
(2)视力在1.0以上(包括1.0)的为正常,则视力正常的有_____人,视力正常的人数占全班人数的___________;
(3)该班学生视力情况________(选填“好”“一般”“差”)
5:我市举行的登山活动中,参加的市民约有12000人,为统计参加活动人员的年龄情况,我们从中抽取了100人的年龄作为样本,进行数据处理,制成扇形统计图和条形统计图如下:
(1)根据扇形统计图提供的信息补全条形统计图;
(2)参加此活动的市民中,哪个年龄段的人数最多?
.
自我评价: 小组评价: 教师评价:
调查统计(3)教学设计
请同学们在预习的基础上,将生成的问题充分交流后,在单位时间内完成下列题目,并准备多元化展示.
带着问题走进丰富多彩的数学世界
问题一:
由于在各个年龄段对节目的爱好有明显的不同,而同一个年龄段对节目的爱好往往存在共性,所以可以对青少年、成年人、老年人各段人群分别进行简单随机抽样,即分层次抽样,使每个年龄段都能抽取一定的人数来代表所在的人群,然后汇总调查结果。
1、那么如何按层次抽取呢?
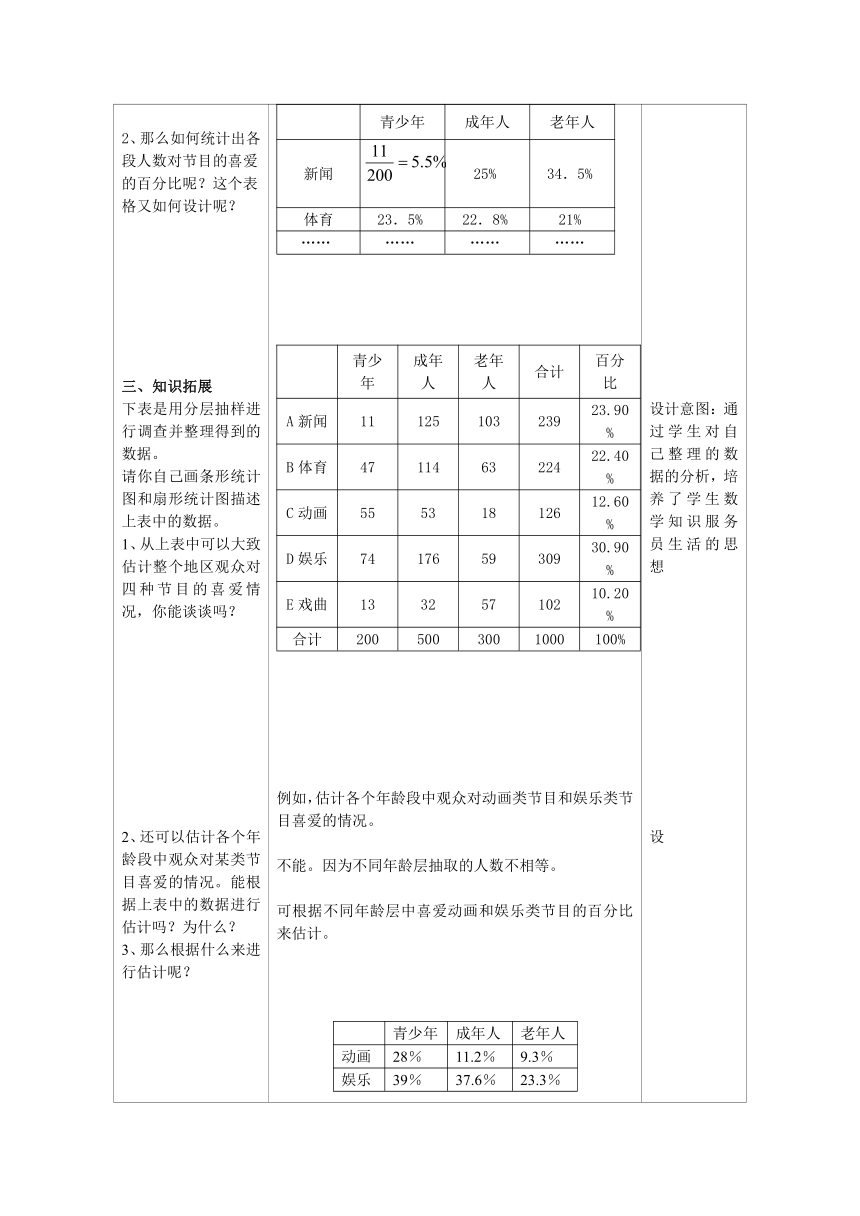
2、那么如何统计出各段人数对节目的喜爱的百分比呢?这个表格又如何设计呢?
问题二:
根据分层抽样进行调查并整理得到的数据。
请你自己画条形统计图和扇形统计图描述上表中的数据。
1、从上表中可以大致估计整个地区观众对四种节目的喜爱情况,你能谈谈吗?
2、还可以估计各个年龄段中观众对某类节目喜爱的情况。能根据上表中的数据进行估计吗?为什么?
3、那么根据什么来进行估计呢?
4、从表中你看到了什么?
5、不同年龄段的观众对节目喜爱不尽相同。用什么方式可以直观地反映这种变化呢?
小组评价: 教师评价:
调查统计(3)教学设计
设计者: 班级: 姓名:
我要飞得更高
【基础达标】
1.下面调查中,适合做全面调查的是( )
A.某品牌的大米在市场上的占有率
B.今天班上有几名同学打扫教室
C.某款汽车每百公里的耗油量
D.春节晚会的收视率
2.下列的调查中,选取的样本具有代表性的有( )
A.为了解某地区居民的防火意识,对该地区的初中生进行调查B.为了解某校1200名学生的视力情况,随机抽取该校120名学生进行调查
C.为了解某商场的平均日营业额,选在周末进行调查
D.为了解全校学生课外小组的活动情况,对该校的男生进行调查
3.在调查一年内某地区降雨的情况时,下列选取样本较为恰当的是( )
A.春、夏、秋、冬各观察一个月B.春、夏、秋、冬各观察一天
C.春天和秋天各观察一个月
D.冬天和夏天各观察一个月
4.某专业户要出售100只羊,现在市场上羊的价格为每千克11元,为了估计这100只羊能卖多少钱,该专业户从中随机抽取5只羊,每只羊的重量如下(单位:千克):26,31,32,36,37
(1)试分别指出上述问题中的总体、个体和样本各是什么;
(2)上述问题中的调查方式是全面调查好还是抽样调查好,请说明你的理由;
(3)估计这100只羊每只羊的平均重量;
(4)估计这100只羊能卖多少钱.
5.在学校体育节前夕,学校体育组想了解全校同学喜欢球类运动的情况,安排体育部长小明负责调查,小明就向本班同学做了调查,由此他得到一批数据.
(1)小明的抽样合适吗?他采取的抽样是简单抽样吗?
(2)请你设计一个简单的随机抽样调查的方案.
【拓展提升】
6.为了解某地区30万电视观众对新闻、动画、娱乐三类节目的喜爱情况,按照老年人、成年人、青少年各年龄段实际人口3∶5∶2的比例,随机抽取一定数量的观众进行调查,得到如下统计图:
(1)上面所用的调查方法是______(填“全面调查”或“抽样调查”);
(2)写出折线统计图中A、B所代表的值;
A:_________ B:__________
(3)求该地区喜爱娱乐节目的成年人的人数.
7.某社区要调查社区居民双休日的学习状况,准备抽查200名居民进行统计,现有下列三种抽查方案:
方案一:从一幢高层住宅楼中选取200名居民;
方案二:从不同住宅楼中随机选取200名居民;
方案三:选取社区内200名在校学生.
(1)上述抽查方案中,最合理的方案是 ;
(2)将最合理的调查方案得到的数据进行汇总,并制成扇形统计图(如图1)和折线统计图(如图2).在这个调查中,200名居民双休日在家学习的有多少人?
(3)请估计该社区2000名居民双休日学习时间不少于4小时的人数,并说明理由.
调查统计(3)教学设计
1.32 2.七年级 3.10 4.(1)6 8 26 (2)24 48% (3)一般
5.(1)略 (2)60——69岁
调查统计(3)教学设计
1.B 2.B 3.B 4.D 5.B
6.(1)抽样调查;
(2)A=20,B=40;
(3) ;100人
7.解:(1)根据题意,分析可得方案二得到的样本最具有代表性,最合理;
(2)根据扇形图,可得被调查的200人中,在家学习的占60%,
故双休日在家学习的有:200×60%=120(人);
(3)由折线图知:双休日学习时间不少于4小时的人数为120人,
故在该社区2000名居民双休日学习时间不少于4小时的人数为 ×2000=1200(人).
30%
10%
百分率
20%
40%
0%
青少年
成年人
老年人
年龄段
娱乐
动画
人数
400
6
年级
7
8
9
200
500
300
100
C等
A等
B等50%
30%
【教材地位分析】
本节是在学习了前两节简单随机抽样和系统抽样的基础上,结合此两种随机抽样特点和适用范围,针对总体的复杂性,为提高样本的代表性,有学习掌握分层抽样这种随机抽样的必要性;为下节“用样本估计总体”的学习打下了基础.因此本节内容具有承前启后的作用,地位重要.
【重点、难点】
重点:正确理解分层抽样的定义,灵活应用分层抽样抽取样本,并恰当的选择三种抽样方法解决现实生活中的抽样问题。
难点:恰当的选择三种抽样方法解决现实生活中的抽样问题。
【教学目标】
知识与技能目标:
(1)正确理解分层抽样的概念;
(2)掌握分层抽样的一般步骤;
(3)区分简单随机抽样、系统抽样和分层抽样,并选择适当正确的方法进行抽样。 过程与方法目标:
通过对现实生活中实际问题进行分层抽样,感知应用数学知识解决实际问题的方法。感悟有具体到一般的研究方法,培养学生的归纳概括能力。
情感与态度目标:
通过对统计学知识的研究,感知数学知识中“估计”与“精确”性的矛盾统一,培养学生的辩证唯物主义的世界观与价值观。
【学生分析】
⑴知识掌握上,虽然学生已经掌握了数据的收集、整理、描述的一些方法,但还很不熟练,尤其扇形统计图的画法和描述,学生掌握很困难,所以有必要作好复习 。
⑵学生学习本节课的知识障碍。对于抽样调查和全面调查的特征学生在观察和归纳方面说的不准确,所以教学中教师应做好示范,适当提示,让学生根据实际情况采取恰当的调查方法;在选取样本时机会可能不均等,提醒学生选取的样本要具有代表性。
【教学方法】
引导学生课前用好《问题导读---评价单》,对所学知识进行提前预习,找出难理解的问题,以便上课更有针对性。
结合本节课的教学内容和学生的认知水平,在教法上,我采用“启发—探究—讨论”式教学模式,充分发挥教师的主导作用,让学生真正成为教学活动的主体。授课过程中注意导学生充分利用《问题生成---评价单》。
然后辅之《问题训练---评价单》进行课堂知识的巩固和验证。
【教师课前准备】
《问题导读---评价单》、《问题生成---评价单》、《问题训练---评价单》
【教学过程设计】
问题与情境 师生行为 设计意图
(一)学前准备,创设情境从上节课我们已经看到在总体数目比较大时,对它进行全面调查很难做到,甚至根本就不可能,如:某地区有百万电视观众,要想了解他们对新闻、体育、动画、娱乐、戏曲五类节目的喜爱情况,能否像上节课中提到的抽100名学生来估计2000名学生的喜爱情况吗?(二)探求新知上述情况显然不能。由于学生、成年人、老年人各自喜爱的节目不一样,所以要了解整个地区的观众的情况,需要在更大范围内抽取样本。由于在各个年龄段对节目的爱好有明显的不同,而同一个年龄段对节目的爱好往往存在共性,所以可以对青少年、成年人、老年人各段人群分别进行简单随机抽样,即分层次抽样,使每个年龄段都能抽取一定的人数来代表所在的人群,然后汇总调查结果。1、那么如何按层次抽取呢?2、那么如何统计出各段人数对节目的喜爱的百分比呢?这个表格又如何设计呢? 三、知识拓展下表是用分层抽样进行调查并整理得到的数据。请你自己画条形统计图和扇形统计图描述上表中的数据。1、从上表中可以大致估计整个地区观众对四种节目的喜爱情况,你能谈谈吗?2、还可以估计各个年龄段中观众对某类节目喜爱的情况。能根据上表中的数据进行估计吗?为什么?3、那么根据什么来进行估计呢?4、从表中你看到了什么?5、不同年龄段的观众对节目喜爱不尽相同。用什么方式可以直观地反映这种变化呢?折线统计图。四、接受考验发放《问题训练---评价单》,学生独立完成上面的练习题五.反思回顾1.通过本课的学习,你学到了哪些新的知识?2.在学习这些知识的过程中,你的经验与教训是什么? 让学生利用课前问题导读评价单进行充分大预习,找出有难点的问题,以增强上课的听课效果。可以按年龄段的实际人口的比例分配来确保每个年龄段都有相应的比例的代表,教材中按青少年、成年人、老年人的人数比为2:5:3抽取请同学们计算按这样的比例各段分别应抽取多少人,并列出表格。青少年成年人老年人合计抽取人数2005003001000在抽取的1000名观众中,对各类节目的喜爱情况整理、绘制成喜爱节目的人数统计表:青少年成年人老年人合计百分比A新闻1112510323923.90%B体育471146322422.40%C动画55531812612.60%D娱乐741765930930.90%E戏曲13325710210.20%合计2005003001000100%先将总体分成几个年龄段(层),然后再在各年龄段(层)中进行简单随机抽样,这是一种分层抽样。分层抽取的样本与这个地区所有观众的年龄结构基本相同,与在整个地区直接进行简单随机抽样相比,更具有代表性。青少年成年人老年人新闻25%34.5%体育23.5%22.8%21%……………………青少年成年人老年人合计百分比A新闻1112510323923.90%B体育471146322422.40%C动画55531812612.60%D娱乐741765930930.90%E戏曲13325710210.20%合计2005003001000100%例如,估计各个年龄段中观众对动画类节目和娱乐类节目喜爱的情况。不能。因为不同年龄层抽取的人数不相等。可根据不同年龄层中喜爱动画和娱乐类节目的百分比来估计。青少年成年人老年人动画28%11.2%9.3%娱乐39%37.6%23.3%下图是不同年龄段观众喜爱娱乐和动画类节目的折线统计图。 从上图中可以清楚地看到,随着年龄的增加,观众对动画类、娱乐类的喜爱程度逐渐下降。 设计意图:实际生活中的问题导入,带给学生轻松愉快的心情,从而也引出了本节课的课题。设计意图:教师提出问题,学生合作讨论,这种教学方法可以让学生体会知识的形成过程,从而加深对知识的理解和运用通过学生合作讨论完成样本的抽取,表格的整理及图形的绘制,使学生体会了知识的形成过程,便于学生理解和记忆。设计意图:通过学生对自己整理的数据的分析,培养了学生数学知识服务员生活的思想 设设计意图:让学灵活运用,加强对知识的理解,题目设计了不同层次的练习题,这样也能使不同水平的学生得到最大程度的发展设计意图:这样可以培养学生归纳总结能力和语言表达能力
调查统计(3)教学设计
设计者: 班级: 姓名:
【教学目标】
知识与技能目标:
(1)正确理解分层抽样的概念;
(2)掌握分层抽样的一般步骤;
(3)区分简单随机抽样、系统抽样和分层抽样,并选择适当正确的方法进行抽样。 过程与方法目标:
通过对现实生活中实际问题进行分层抽样,感知应用数学知识解决实际问题的方法。感悟有具体到一般的研究方法,培养学生的归纳概括能力。
情感与态度目标:
通过对统计学知识的研究,感知数学知识中“估计”与“精确”性的矛盾统一,培养学生的辩证唯物主义的世界观与价值观。
为你导航
1、在扇形统计图中,有两个扇形的圆心角度数之比为3∶4,且较小扇形表示24本课本书,则较大扇形表示________本课本书.
2、如图,某校四个年级男女生人数的条形统计图,则学生最多的年级是 .
3、据统计,某班50名学生参加2011年初中毕业生学业考试,综合评价等级为A,B,C等的学生情况如扇形图所示,则该班得A等的学生有______名.
4、某班50名学生右眼视力的检查结果如下表:
视力 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 1.0 1.2 1.5
人数 1 1 3 4 3 4 4 6 8 10 6
(1)视力为1.5的有_____人,视力为1.0的有______人,视力小于1.0的有______人.
(2)视力在1.0以上(包括1.0)的为正常,则视力正常的有_____人,视力正常的人数占全班人数的___________;
(3)该班学生视力情况________(选填“好”“一般”“差”)
5:我市举行的登山活动中,参加的市民约有12000人,为统计参加活动人员的年龄情况,我们从中抽取了100人的年龄作为样本,进行数据处理,制成扇形统计图和条形统计图如下:
(1)根据扇形统计图提供的信息补全条形统计图;
(2)参加此活动的市民中,哪个年龄段的人数最多?
.
自我评价: 小组评价: 教师评价:
调查统计(3)教学设计
请同学们在预习的基础上,将生成的问题充分交流后,在单位时间内完成下列题目,并准备多元化展示.
带着问题走进丰富多彩的数学世界
问题一:
由于在各个年龄段对节目的爱好有明显的不同,而同一个年龄段对节目的爱好往往存在共性,所以可以对青少年、成年人、老年人各段人群分别进行简单随机抽样,即分层次抽样,使每个年龄段都能抽取一定的人数来代表所在的人群,然后汇总调查结果。
1、那么如何按层次抽取呢?
2、那么如何统计出各段人数对节目的喜爱的百分比呢?这个表格又如何设计呢?
问题二:
根据分层抽样进行调查并整理得到的数据。
请你自己画条形统计图和扇形统计图描述上表中的数据。
1、从上表中可以大致估计整个地区观众对四种节目的喜爱情况,你能谈谈吗?
2、还可以估计各个年龄段中观众对某类节目喜爱的情况。能根据上表中的数据进行估计吗?为什么?
3、那么根据什么来进行估计呢?
4、从表中你看到了什么?
5、不同年龄段的观众对节目喜爱不尽相同。用什么方式可以直观地反映这种变化呢?
小组评价: 教师评价:
调查统计(3)教学设计
设计者: 班级: 姓名:
我要飞得更高
【基础达标】
1.下面调查中,适合做全面调查的是( )
A.某品牌的大米在市场上的占有率
B.今天班上有几名同学打扫教室
C.某款汽车每百公里的耗油量
D.春节晚会的收视率
2.下列的调查中,选取的样本具有代表性的有( )
A.为了解某地区居民的防火意识,对该地区的初中生进行调查B.为了解某校1200名学生的视力情况,随机抽取该校120名学生进行调查
C.为了解某商场的平均日营业额,选在周末进行调查
D.为了解全校学生课外小组的活动情况,对该校的男生进行调查
3.在调查一年内某地区降雨的情况时,下列选取样本较为恰当的是( )
A.春、夏、秋、冬各观察一个月B.春、夏、秋、冬各观察一天
C.春天和秋天各观察一个月
D.冬天和夏天各观察一个月
4.某专业户要出售100只羊,现在市场上羊的价格为每千克11元,为了估计这100只羊能卖多少钱,该专业户从中随机抽取5只羊,每只羊的重量如下(单位:千克):26,31,32,36,37
(1)试分别指出上述问题中的总体、个体和样本各是什么;
(2)上述问题中的调查方式是全面调查好还是抽样调查好,请说明你的理由;
(3)估计这100只羊每只羊的平均重量;
(4)估计这100只羊能卖多少钱.
5.在学校体育节前夕,学校体育组想了解全校同学喜欢球类运动的情况,安排体育部长小明负责调查,小明就向本班同学做了调查,由此他得到一批数据.
(1)小明的抽样合适吗?他采取的抽样是简单抽样吗?
(2)请你设计一个简单的随机抽样调查的方案.
【拓展提升】
6.为了解某地区30万电视观众对新闻、动画、娱乐三类节目的喜爱情况,按照老年人、成年人、青少年各年龄段实际人口3∶5∶2的比例,随机抽取一定数量的观众进行调查,得到如下统计图:
(1)上面所用的调查方法是______(填“全面调查”或“抽样调查”);
(2)写出折线统计图中A、B所代表的值;
A:_________ B:__________
(3)求该地区喜爱娱乐节目的成年人的人数.
7.某社区要调查社区居民双休日的学习状况,准备抽查200名居民进行统计,现有下列三种抽查方案:
方案一:从一幢高层住宅楼中选取200名居民;
方案二:从不同住宅楼中随机选取200名居民;
方案三:选取社区内200名在校学生.
(1)上述抽查方案中,最合理的方案是 ;
(2)将最合理的调查方案得到的数据进行汇总,并制成扇形统计图(如图1)和折线统计图(如图2).在这个调查中,200名居民双休日在家学习的有多少人?
(3)请估计该社区2000名居民双休日学习时间不少于4小时的人数,并说明理由.
调查统计(3)教学设计
1.32 2.七年级 3.10 4.(1)6 8 26 (2)24 48% (3)一般
5.(1)略 (2)60——69岁
调查统计(3)教学设计
1.B 2.B 3.B 4.D 5.B
6.(1)抽样调查;
(2)A=20,B=40;
(3) ;100人
7.解:(1)根据题意,分析可得方案二得到的样本最具有代表性,最合理;
(2)根据扇形图,可得被调查的200人中,在家学习的占60%,
故双休日在家学习的有:200×60%=120(人);
(3)由折线图知:双休日学习时间不少于4小时的人数为120人,
故在该社区2000名居民双休日学习时间不少于4小时的人数为 ×2000=1200(人).
30%
10%
百分率
20%
40%
0%
青少年
成年人
老年人
年龄段
娱乐
动画
人数
400
6
年级
7
8
9
200
500
300
100
C等
A等
B等50%
30%
