2.1.2指数函数及其性质(三)
文档属性
| 名称 | 2.1.2指数函数及其性质(三) |

|
|
| 格式 | zip | ||
| 文件大小 | 236.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-08-02 00:00:00 | ||
图片预览


文档简介
(共37张PPT)
2.1.2指数函数
及其性质
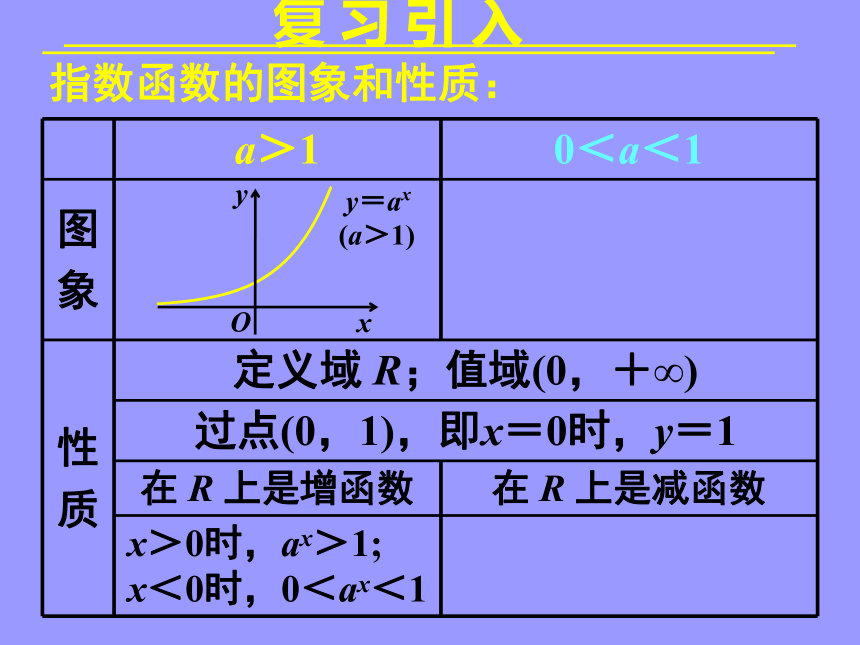
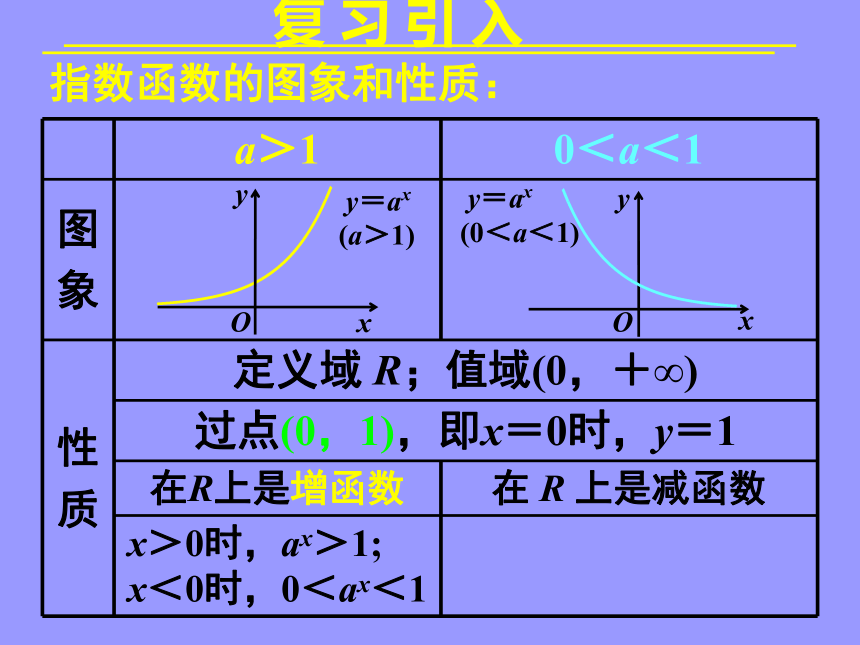
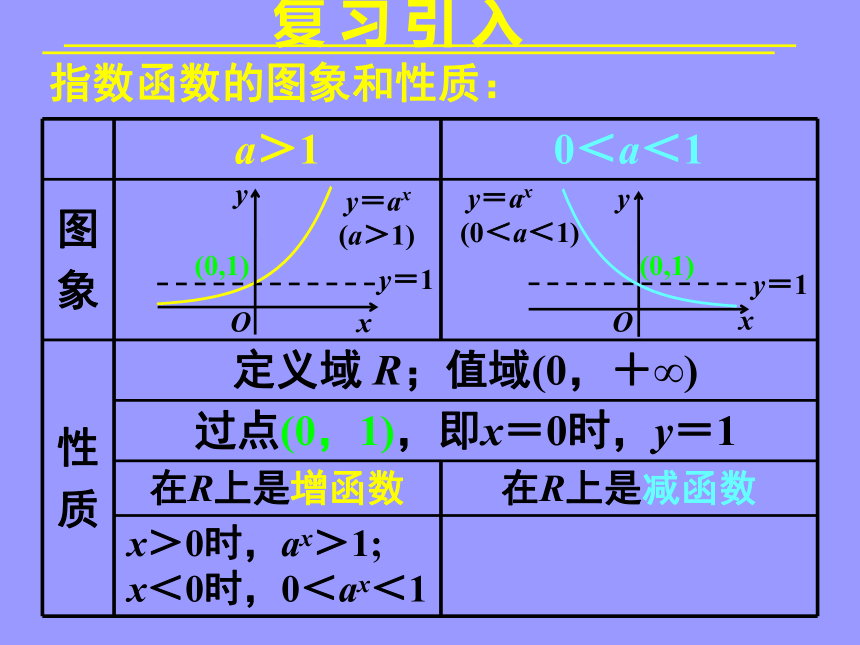
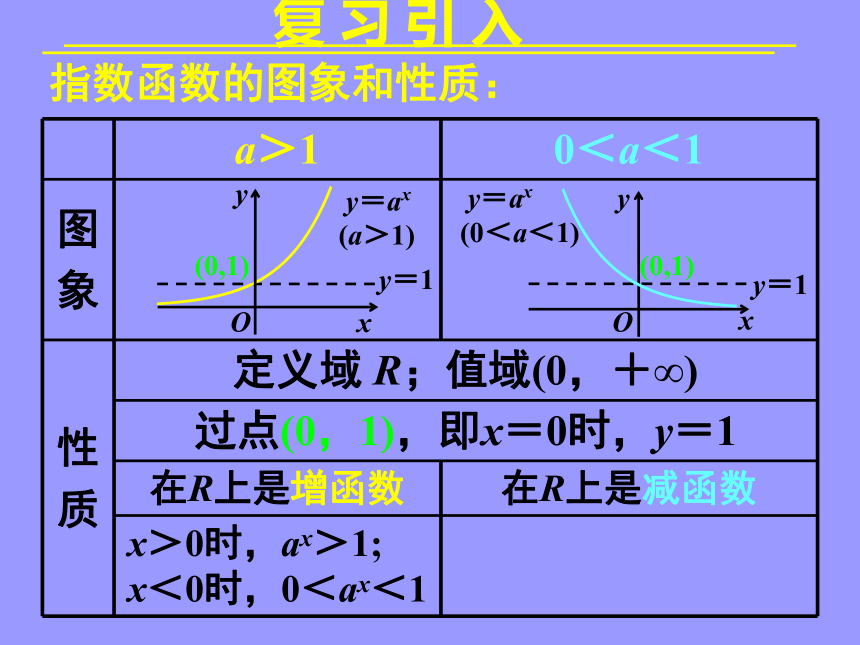
复 习 引 入
a>1 0<a<1
图
象
性
质 定义域 R;值域(0,+∞)
过点(0,1),即x=0时,y=1
在 R 上是增函数 在 R 上是减函数
x>0时,ax>1;
x<0时,0<ax<1
指数函数的图象和性质:
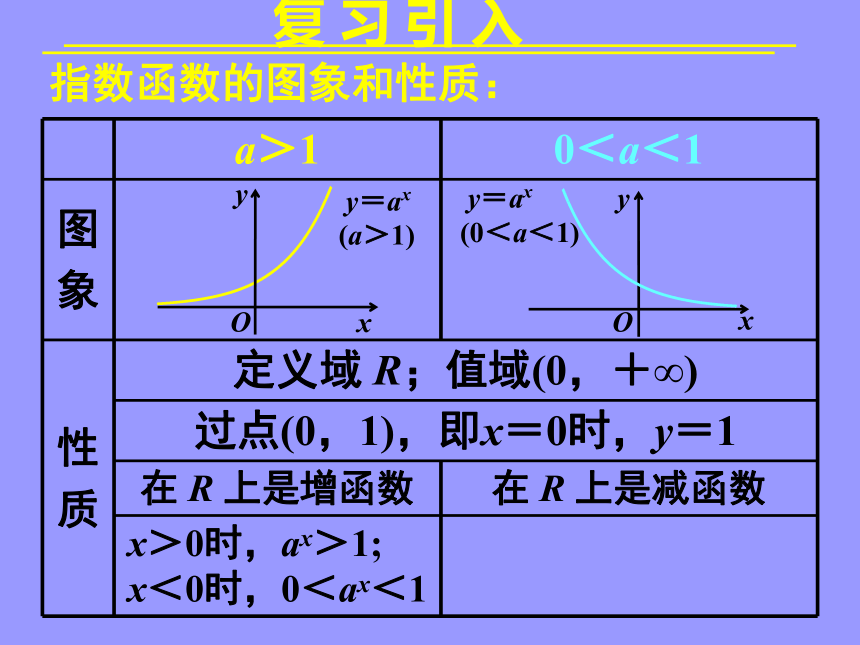
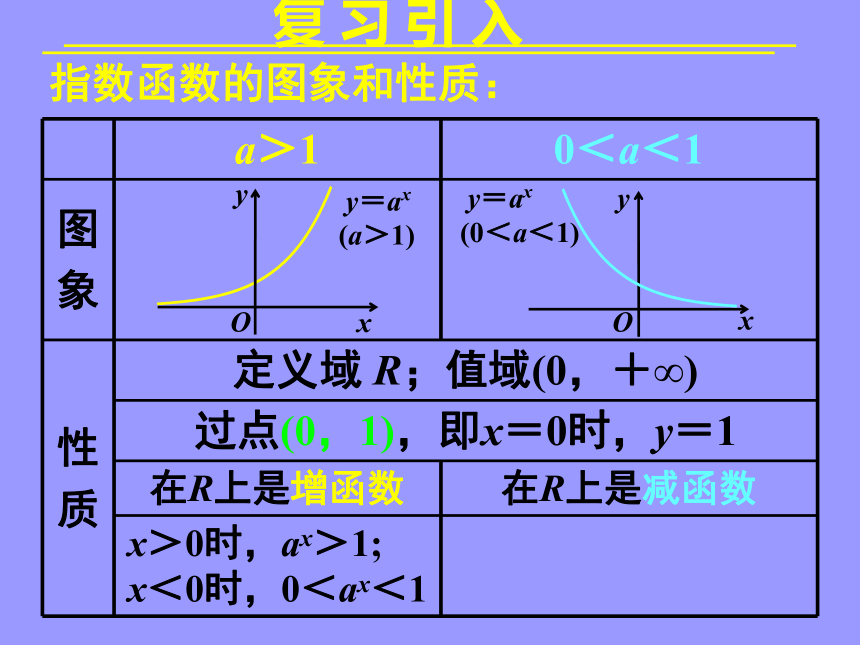
复 习 引 入
a>1 0<a<1
图
象
性
质 定义域 R;值域(0,+∞)
过点(0,1),即x=0时,y=1
在 R 上是增函数 在 R 上是减函数
x>0时,ax>1;
x<0时,0<ax<1
指数函数的图象和性质:
x
y
y=ax
(a>1)
O
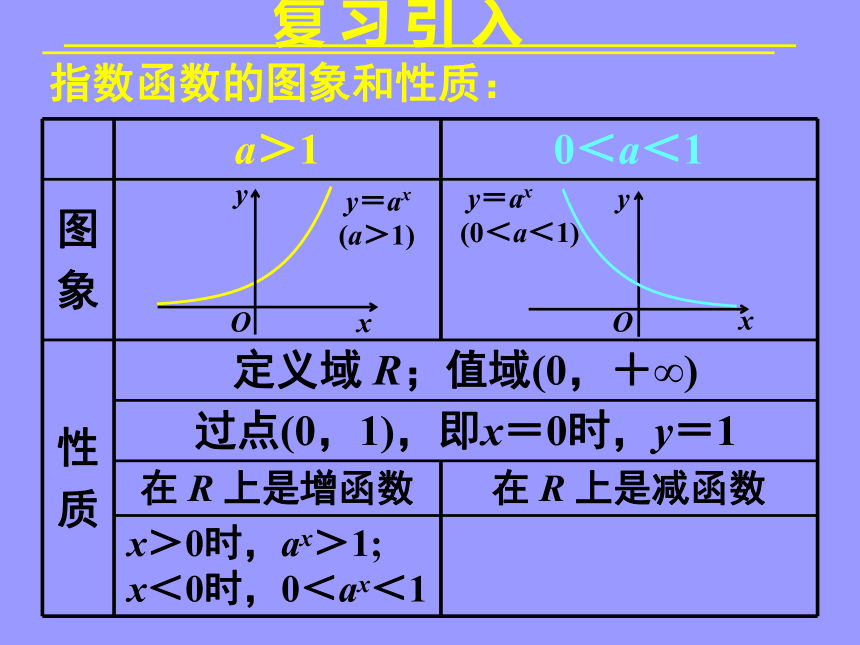
复 习 引 入
a>1 0<a<1
图
象
性
质 定义域 R;值域(0,+∞)
过点(0,1),即x=0时,y=1
在 R 上是增函数 在 R 上是减函数
x>0时,ax>1;
x<0时,0<ax<1
指数函数的图象和性质:
x
y
y=ax
(a>1)
O
x
y
y=ax
(0<a<1)
O
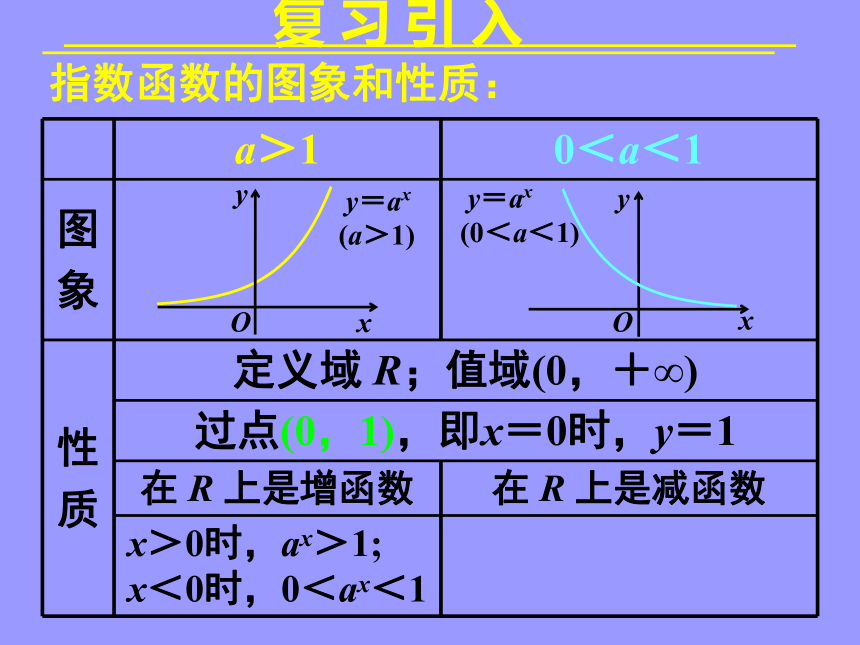
复 习 引 入
a>1 0<a<1
图
象
性
质 定义域 R;值域(0,+∞)
过点(0,1),即x=0时,y=1
在 R 上是增函数 在 R 上是减函数
x>0时,ax>1;
x<0时,0<ax<1
指数函数的图象和性质:
x
y
y=ax
(a>1)
O
x
y
y=ax
(0<a<1)
O
复 习 引 入
a>1 0<a<1
图
象
性
质 定义域 R;值域(0,+∞)
过点(0,1),即x=0时,y=1
在 R 上是增函数 在 R 上是减函数
x>0时,ax>1;
x<0时,0<ax<1
指数函数的图象和性质:
x
y
y=ax
(a>1)
O
x
y
y=ax
(0<a<1)
O
复 习 引 入
a>1 0<a<1
图
象
性
质 定义域 R;值域(0,+∞)
过点(0,1),即x=0时,y=1
在R上是增函数 在 R 上是减函数
x>0时,ax>1;
x<0时,0<ax<1
指数函数的图象和性质:
x
y
y=ax
(a>1)
O
x
y
y=ax
(0<a<1)
O
复 习 引 入
a>1 0<a<1
图
象
性
质 定义域 R;值域(0,+∞)
过点(0,1),即x=0时,y=1
在R上是增函数 在R上是减函数
x>0时,ax>1;
x<0时,0<ax<1
指数函数的图象和性质:
x
y
y=ax
(a>1)
O
x
y
y=ax
(0<a<1)
O
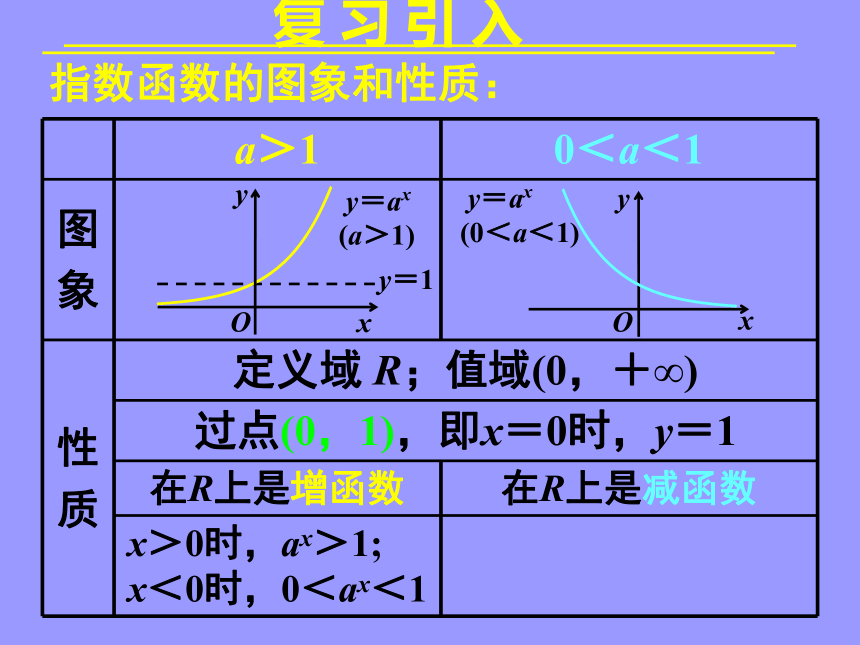
复 习 引 入
a>1 0<a<1
图
象
性
质 定义域 R;值域(0,+∞)
过点(0,1),即x=0时,y=1
在R上是增函数 在R上是减函数
x>0时,ax>1;
x<0时,0<ax<1
指数函数的图象和性质:
y=1
x
y
y=ax
(a>1)
O
x
y
y=ax
(0<a<1)
O
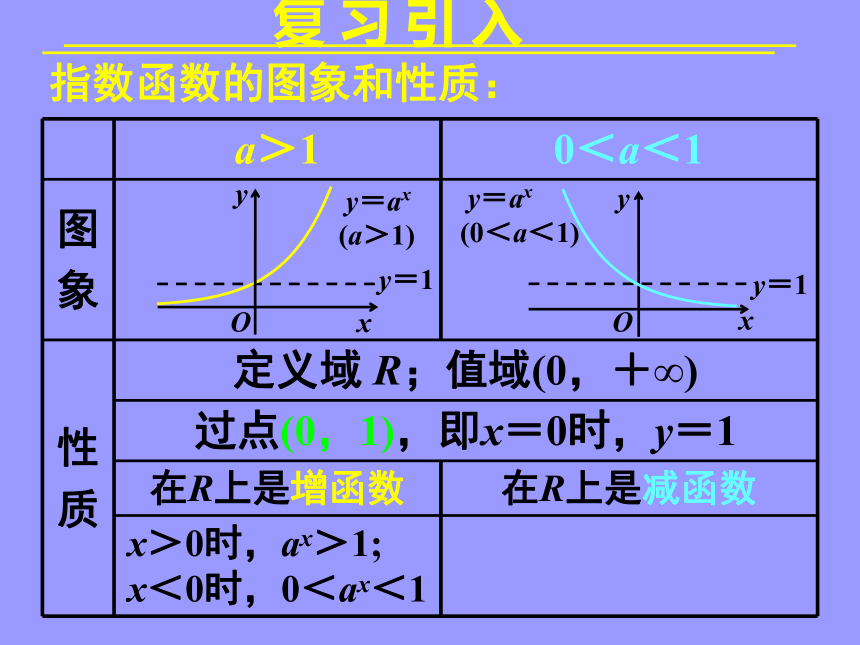
复 习 引 入
a>1 0<a<1
图
象
性
质 定义域 R;值域(0,+∞)
过点(0,1),即x=0时,y=1
在R上是增函数 在R上是减函数
x>0时,ax>1;
x<0时,0<ax<1
指数函数的图象和性质:
y=1
x
y
y=ax
(a>1)
O
y=1
x
y
y=ax
(0<a<1)
O
复 习 引 入
a>1 0<a<1
图
象
性
质 定义域 R;值域(0,+∞)
过点(0,1),即x=0时,y=1
在R上是增函数 在R上是减函数
x>0时,ax>1;
x<0时,0<ax<1
指数函数的图象和性质:
y=1
x
y
y=ax
(a>1)
O
y=1
x
y
y=ax
(0<a<1)
O
(0,1)
(0,1)
复 习 引 入
a>1 0<a<1
图
象
性
质 定义域 R;值域(0,+∞)
过点(0,1),即x=0时,y=1
在R上是增函数 在R上是减函数
x>0时,ax>1;
x<0时,0<ax<1
指数函数的图象和性质:
y=1
x
y
y=ax
(a>1)
O
y=1
x
y
y=ax
(0<a<1)
O
(0,1)
(0,1)
复 习 引 入
a>1 0<a<1
图
象
性
质 定义域 R;值域(0,+∞)
过点(0,1),即x=0时,y=1
在R上是增函数 在R上是减函数
x>0时,ax>1;
x<0时,0<ax<1 x>0时,0<ax<1;
x<0时,ax>1
指数函数的图象和性质:
y=1
x
y
y=ax
(a>1)
O
y=1
x
y
y=ax
(0<a<1)
O
(0,1)
(0,1)
1.解不等式:
练习
复 习 引 入
2.
练习
复 习 引 入
复 习 引 入
3. 函数y=a x-1+4恒过定点 .
A.(1,5) B.(1,4)
C.(0,4) D.(4,0)
练习
4. 下列函数中,值域为(0,+∞)的函数
是 ( )
复 习 引 入
练习
讲 授 新 课
1.说明下列函数图象与指数函数y=2x的
图象关系,并画出它们的图象:
一、指数函数图象的变换
x -3 -2 -1 0 1 2 3
0.125 0.25 0.5 1 2 4 8
0.25 0.5 1 2 4 8 16
0.5 1 2 4 8 16 32
作出图象,显示出函数数据表
9
8
7
6
5
4
3
2
1
-4
-2
2
4
O
x
y
9
8
7
6
5
4
3
2
1
-4
-2
2
4
O
x
y
9
8
7
6
5
4
3
2
1
-4
-2
2
4
O
x
y
x -3 -2 -1 0 1 2 3
0.125 0.25 0.5 1 2 4 8
0.0625 0.125 0.25 0.5 1 2 4
0.03125 0.0625 0.125 0.25 0.5 1 2
作出图象,显示出函数数据表
9
8
7
6
5
4
3
2
1
-4
-2
2
4
O
x
y
9
8
7
6
5
4
3
2
1
-4
-2
2
4
O
x
y
9
8
7
6
5
4
3
2
1
-4
-2
2
4
O
x
y
9
8
7
6
5
4
3
2
1
-4
-2
2
4
O
x
y
9
8
7
6
5
4
3
2
1
-4
-2
2
4
O
x
y
9
8
7
6
5
4
3
2
1
-4
-2
2
4
O
x
y
小 结:
向左平移a个单位得到f(x+a)的图象;
向右平移a个单位得到f(x-a)的图象;
向上平移a个单位得到f(x)+a的图象;
向下平移a个单位得到f(x)-a的图象.
f(x)的图象
小 结:
例 某种放射性物质不断变化为其他物
质,每经过1年剩留的这种物质是原来
的84%. 画出这种物质的剩留量随时间
变化的图象,并从图象上求出经过多少
年,剩留量是原来的一半 (结果保留一
个有效数字).
二、实际问题
课 堂 小 结
1. 指数复合函数的单调性;
2. 指数函数图象的变换.
1.阅读教材P.54-P.58;
2.《习案》作业十九.
课 后 作 业
2.1.2指数函数
及其性质
复 习 引 入
a>1 0<a<1
图
象
性
质 定义域 R;值域(0,+∞)
过点(0,1),即x=0时,y=1
在 R 上是增函数 在 R 上是减函数
x>0时,ax>1;
x<0时,0<ax<1
指数函数的图象和性质:
复 习 引 入
a>1 0<a<1
图
象
性
质 定义域 R;值域(0,+∞)
过点(0,1),即x=0时,y=1
在 R 上是增函数 在 R 上是减函数
x>0时,ax>1;
x<0时,0<ax<1
指数函数的图象和性质:
x
y
y=ax
(a>1)
O
复 习 引 入
a>1 0<a<1
图
象
性
质 定义域 R;值域(0,+∞)
过点(0,1),即x=0时,y=1
在 R 上是增函数 在 R 上是减函数
x>0时,ax>1;
x<0时,0<ax<1
指数函数的图象和性质:
x
y
y=ax
(a>1)
O
x
y
y=ax
(0<a<1)
O
复 习 引 入
a>1 0<a<1
图
象
性
质 定义域 R;值域(0,+∞)
过点(0,1),即x=0时,y=1
在 R 上是增函数 在 R 上是减函数
x>0时,ax>1;
x<0时,0<ax<1
指数函数的图象和性质:
x
y
y=ax
(a>1)
O
x
y
y=ax
(0<a<1)
O
复 习 引 入
a>1 0<a<1
图
象
性
质 定义域 R;值域(0,+∞)
过点(0,1),即x=0时,y=1
在 R 上是增函数 在 R 上是减函数
x>0时,ax>1;
x<0时,0<ax<1
指数函数的图象和性质:
x
y
y=ax
(a>1)
O
x
y
y=ax
(0<a<1)
O
复 习 引 入
a>1 0<a<1
图
象
性
质 定义域 R;值域(0,+∞)
过点(0,1),即x=0时,y=1
在R上是增函数 在 R 上是减函数
x>0时,ax>1;
x<0时,0<ax<1
指数函数的图象和性质:
x
y
y=ax
(a>1)
O
x
y
y=ax
(0<a<1)
O
复 习 引 入
a>1 0<a<1
图
象
性
质 定义域 R;值域(0,+∞)
过点(0,1),即x=0时,y=1
在R上是增函数 在R上是减函数
x>0时,ax>1;
x<0时,0<ax<1
指数函数的图象和性质:
x
y
y=ax
(a>1)
O
x
y
y=ax
(0<a<1)
O
复 习 引 入
a>1 0<a<1
图
象
性
质 定义域 R;值域(0,+∞)
过点(0,1),即x=0时,y=1
在R上是增函数 在R上是减函数
x>0时,ax>1;
x<0时,0<ax<1
指数函数的图象和性质:
y=1
x
y
y=ax
(a>1)
O
x
y
y=ax
(0<a<1)
O
复 习 引 入
a>1 0<a<1
图
象
性
质 定义域 R;值域(0,+∞)
过点(0,1),即x=0时,y=1
在R上是增函数 在R上是减函数
x>0时,ax>1;
x<0时,0<ax<1
指数函数的图象和性质:
y=1
x
y
y=ax
(a>1)
O
y=1
x
y
y=ax
(0<a<1)
O
复 习 引 入
a>1 0<a<1
图
象
性
质 定义域 R;值域(0,+∞)
过点(0,1),即x=0时,y=1
在R上是增函数 在R上是减函数
x>0时,ax>1;
x<0时,0<ax<1
指数函数的图象和性质:
y=1
x
y
y=ax
(a>1)
O
y=1
x
y
y=ax
(0<a<1)
O
(0,1)
(0,1)
复 习 引 入
a>1 0<a<1
图
象
性
质 定义域 R;值域(0,+∞)
过点(0,1),即x=0时,y=1
在R上是增函数 在R上是减函数
x>0时,ax>1;
x<0时,0<ax<1
指数函数的图象和性质:
y=1
x
y
y=ax
(a>1)
O
y=1
x
y
y=ax
(0<a<1)
O
(0,1)
(0,1)
复 习 引 入
a>1 0<a<1
图
象
性
质 定义域 R;值域(0,+∞)
过点(0,1),即x=0时,y=1
在R上是增函数 在R上是减函数
x>0时,ax>1;
x<0时,0<ax<1 x>0时,0<ax<1;
x<0时,ax>1
指数函数的图象和性质:
y=1
x
y
y=ax
(a>1)
O
y=1
x
y
y=ax
(0<a<1)
O
(0,1)
(0,1)
1.解不等式:
练习
复 习 引 入
2.
练习
复 习 引 入
复 习 引 入
3. 函数y=a x-1+4恒过定点 .
A.(1,5) B.(1,4)
C.(0,4) D.(4,0)
练习
4. 下列函数中,值域为(0,+∞)的函数
是 ( )
复 习 引 入
练习
讲 授 新 课
1.说明下列函数图象与指数函数y=2x的
图象关系,并画出它们的图象:
一、指数函数图象的变换
x -3 -2 -1 0 1 2 3
0.125 0.25 0.5 1 2 4 8
0.25 0.5 1 2 4 8 16
0.5 1 2 4 8 16 32
作出图象,显示出函数数据表
9
8
7
6
5
4
3
2
1
-4
-2
2
4
O
x
y
9
8
7
6
5
4
3
2
1
-4
-2
2
4
O
x
y
9
8
7
6
5
4
3
2
1
-4
-2
2
4
O
x
y
x -3 -2 -1 0 1 2 3
0.125 0.25 0.5 1 2 4 8
0.0625 0.125 0.25 0.5 1 2 4
0.03125 0.0625 0.125 0.25 0.5 1 2
作出图象,显示出函数数据表
9
8
7
6
5
4
3
2
1
-4
-2
2
4
O
x
y
9
8
7
6
5
4
3
2
1
-4
-2
2
4
O
x
y
9
8
7
6
5
4
3
2
1
-4
-2
2
4
O
x
y
9
8
7
6
5
4
3
2
1
-4
-2
2
4
O
x
y
9
8
7
6
5
4
3
2
1
-4
-2
2
4
O
x
y
9
8
7
6
5
4
3
2
1
-4
-2
2
4
O
x
y
小 结:
向左平移a个单位得到f(x+a)的图象;
向右平移a个单位得到f(x-a)的图象;
向上平移a个单位得到f(x)+a的图象;
向下平移a个单位得到f(x)-a的图象.
f(x)的图象
小 结:
例 某种放射性物质不断变化为其他物
质,每经过1年剩留的这种物质是原来
的84%. 画出这种物质的剩留量随时间
变化的图象,并从图象上求出经过多少
年,剩留量是原来的一半 (结果保留一
个有效数字).
二、实际问题
课 堂 小 结
1. 指数复合函数的单调性;
2. 指数函数图象的变换.
1.阅读教材P.54-P.58;
2.《习案》作业十九.
课 后 作 业
