四年级数学上册-2.13.图形的旋转课件浙教版(16张ppt)
文档属性
| 名称 | 四年级数学上册-2.13.图形的旋转课件浙教版(16张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-29 18:59:49 | ||
图片预览





文档简介
平移变换
轴对称变换
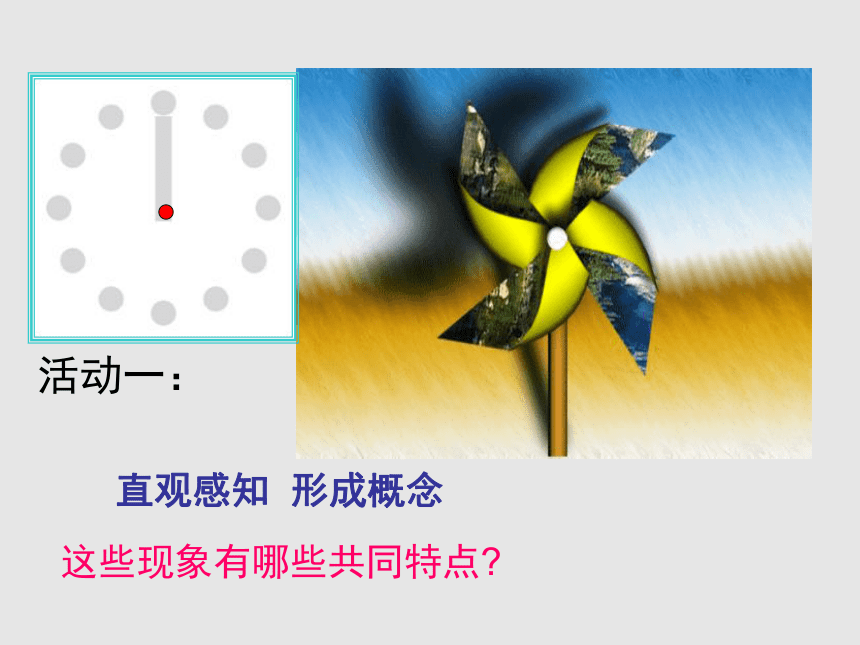
活动一:
这些现象有哪些共同特点?
直观感知 形成概念
1、由一个图形改变为另一个图形,在改变的过程
中,原图形上的所有点都绕 ,按
,转动 ,这样的图形
改变叫做图形的旋转变换,简称旋转。
这个固定的点叫做___________。
旋转的角度叫__________.
一个固定的点
同一个方向
同一个角度
叙述一个旋转变换要注意旋转变换的三个要素:
1、旋转中心;
2、旋转的方向;
3、旋转的角度。
什么是图形的旋转呢?
旋转中心
旋转角
1.举出一些现实生活中旋转的实例.
2.下列现象中属于旋转的有( )个
①地下水位逐年下降;②滑雪运动员在雪地上滑行;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动.
A.2 B.3 C.4 D.5
C
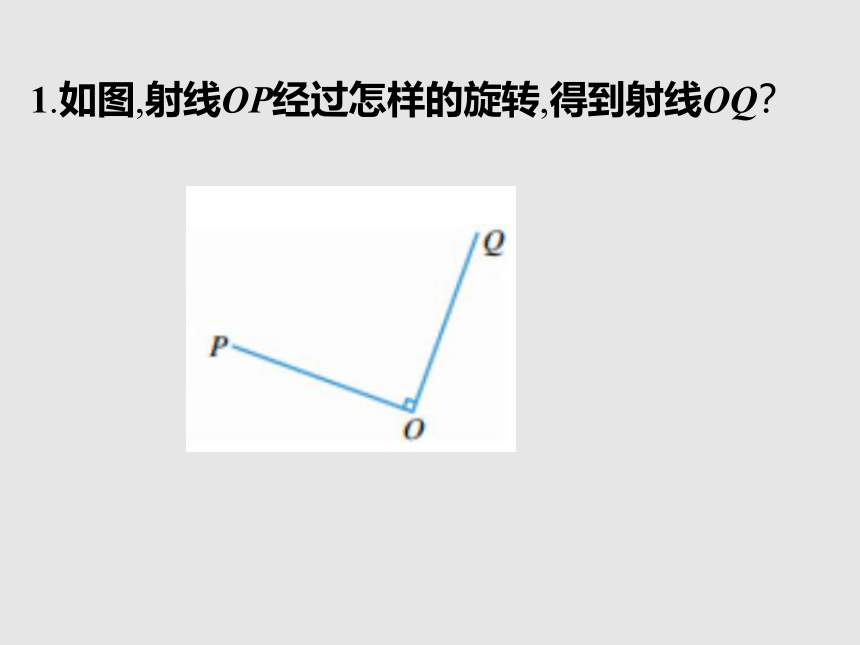
1.如图,射线OP经过怎样的旋转,得到射线OQ?
O
A
A′
80?
1、求点A绕点O顺时针旋转80?后的图形A’B’
2.线段的旋转变换:线段AB绕着O点顺时针旋转90°后的图形A’B’
旋转中心
90 °
原线段
旋转后的线段
A
B
A’
B’
90 °
O
线段A’B’就是所求作的旋转变换后的图形
3、如图,O是△ABC外一点。以点O为旋转中心,将△ABC按逆时针旋转80°,作出经旋转变换后的图形,说出作图过程。
(1).以o为旋转中心,分别把点A,B,C按逆时针方向旋转80°,得到点A’,B’,C’。
(2).连接A’B’,B’C’,C’A’, △A’B’C’就是所求作的经旋转后的图形。
⑴旋转中心是什么?
旋转角是什么?
⑵经过旋转,点
A、B、C分别
移动到什么位置?
⑶AO与A’O的长有
什么关系?
BO与B’O呢?
⑷∠AOA’与∠BOB’
有什么大小关系?
问:通过对以上的讨论,旋转变换有些什么性质?
旋转的基本性质
(1)图形经过旋转所得的图形和原图形全等.
(2)对应点到旋转中心的距离相等.
(3)任意一对对应点与旋转中心的连线所成的
角度都是旋转的角度.
(4)图形上的每一点都绕旋转中心沿相同方向
转动了相同的角度
当图形旋转的角度为180°时,所得的图形和原图形关于旋转中心成中心对称
2、如图,△ABC与△ADE都是等腰直角三角形,∠C和∠AED都是直角,点E在AB上,如果△ABC经旋转后能与△ADE重合,点 是旋转中心,旋转了 度。
点B的对应点是点 ;线段AB的对应线段是 ;∠ABC的对应角是 。
A
45
D
AD
∠ADE
3、如图所示是一双手的图片。你认为能否经过一定的旋转变换,使左手的图形与右手的图形重合?经过轴对称变换呢?用你的左、右手试一试。
旋转变换必须指明:
1、旋转中心,
2、旋转方向,
3、旋转角度.
旋转变换与轴对称变换、平移变换有何异同点?
特征
运动方式
形状
大小
方向
轴对称
平移
旋转
不变
不变
改变
不变
不变
不变
不变
不变
改变
轴对称变换
活动一:
这些现象有哪些共同特点?
直观感知 形成概念
1、由一个图形改变为另一个图形,在改变的过程
中,原图形上的所有点都绕 ,按
,转动 ,这样的图形
改变叫做图形的旋转变换,简称旋转。
这个固定的点叫做___________。
旋转的角度叫__________.
一个固定的点
同一个方向
同一个角度
叙述一个旋转变换要注意旋转变换的三个要素:
1、旋转中心;
2、旋转的方向;
3、旋转的角度。
什么是图形的旋转呢?
旋转中心
旋转角
1.举出一些现实生活中旋转的实例.
2.下列现象中属于旋转的有( )个
①地下水位逐年下降;②滑雪运动员在雪地上滑行;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动.
A.2 B.3 C.4 D.5
C
1.如图,射线OP经过怎样的旋转,得到射线OQ?
O
A
A′
80?
1、求点A绕点O顺时针旋转80?后的图形A’B’
2.线段的旋转变换:线段AB绕着O点顺时针旋转90°后的图形A’B’
旋转中心
90 °
原线段
旋转后的线段
A
B
A’
B’
90 °
O
线段A’B’就是所求作的旋转变换后的图形
3、如图,O是△ABC外一点。以点O为旋转中心,将△ABC按逆时针旋转80°,作出经旋转变换后的图形,说出作图过程。
(1).以o为旋转中心,分别把点A,B,C按逆时针方向旋转80°,得到点A’,B’,C’。
(2).连接A’B’,B’C’,C’A’, △A’B’C’就是所求作的经旋转后的图形。
⑴旋转中心是什么?
旋转角是什么?
⑵经过旋转,点
A、B、C分别
移动到什么位置?
⑶AO与A’O的长有
什么关系?
BO与B’O呢?
⑷∠AOA’与∠BOB’
有什么大小关系?
问:通过对以上的讨论,旋转变换有些什么性质?
旋转的基本性质
(1)图形经过旋转所得的图形和原图形全等.
(2)对应点到旋转中心的距离相等.
(3)任意一对对应点与旋转中心的连线所成的
角度都是旋转的角度.
(4)图形上的每一点都绕旋转中心沿相同方向
转动了相同的角度
当图形旋转的角度为180°时,所得的图形和原图形关于旋转中心成中心对称
2、如图,△ABC与△ADE都是等腰直角三角形,∠C和∠AED都是直角,点E在AB上,如果△ABC经旋转后能与△ADE重合,点 是旋转中心,旋转了 度。
点B的对应点是点 ;线段AB的对应线段是 ;∠ABC的对应角是 。
A
45
D
AD
∠ADE
3、如图所示是一双手的图片。你认为能否经过一定的旋转变换,使左手的图形与右手的图形重合?经过轴对称变换呢?用你的左、右手试一试。
旋转变换必须指明:
1、旋转中心,
2、旋转方向,
3、旋转角度.
旋转变换与轴对称变换、平移变换有何异同点?
特征
运动方式
形状
大小
方向
轴对称
平移
旋转
不变
不变
改变
不变
不变
不变
不变
不变
改变
同课章节目录
- 一 除数是两位数的除法
- 1、商是两位数的除法
- 2、商是一位数的除法(一)
- 3、商是一位数的除法(二)
- 4、商不变的性质
- 5、应用问题
- 二 几何小天地
- 6、线段、射线和直线
- 7、线段的计数
- 8、两点间的距离
- 9、图形的平移
- 10、垂直与平行
- 11、画垂线和平行线
- 12、确定位置
- 13、图形的旋转
- 14、认识圆
- 15、角的认识
- 三 统计
- 16、数据的调查与分类
- 17、条形统计图(一)
- 18、条形统计图(二)
- 四 混合运算与应用问题
- 19、应用问题(一)
- 20、应用问题(二)
- 21、应用问题(三)
- 22、中括号
- 23、计算器
- 24、探索规律
- 五 万以上的数
- 25、十进制计算法
- 26、万以上数的读法
- 27、万以上数的写法
- 28、三位数乘两位数
- 29、近似数
- 六 总复习
- 总复习
