2.6利用三角函数测高同步训练(附答案)-2021--2022学年鲁教版(五四制)九年级数学上册
文档属性
| 名称 | 2.6利用三角函数测高同步训练(附答案)-2021--2022学年鲁教版(五四制)九年级数学上册 |

|
|
| 格式 | doc | ||
| 文件大小 | 359.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-31 00:00:00 | ||
图片预览




文档简介
2021年鲁教版九年级数学上册《2.6利用三角函数测高》同步优生辅导训练(附答案)
1.如图,一艘船从A处向北偏东30°的方向行驶10千米到B处,再从B处向正西方向行驶20千米到C处,这时这艘船与A的距离( )
A.15千米 B.10千米 C.10千米 D.5千米
2.已知海面上一艘货轮A在灯塔B的北偏东30°方向,海监船C在灯塔B的正东方向5海里处,此时海监船C发现货轮A在它的正北方向,那么海监船C与货轮A的距离是( )A.10海里 B.5海里 C.5海里 D.海里
3.如果从货船A测得小岛b在货船A的北偏东30°方向500米处,那么从小岛B看货船A的位置,此时货船A在小岛B的( )
A.南偏西30°方向500米处 B.南偏西60°方向500米处
C.南偏西30°方向250米处 D.南偏西60°方向250米处
4.如图,一艘轮船由西向东航行,在A处测得灯塔P在北偏东60°的方向,继续向东航行40海里后到B处,测得灯塔P在北偏东30°的方向,此时轮船与灯塔之间的距离是 海里.
5.如图,在一条东西方向笔直的沿湖道路l上有A、B两个游船码头,观光岛屿C在码头A的北偏东60°方向、在码头B的北偏西45°方向,AC=4千米.那么码头A、B之间的距离等于 千米.(结果保留根号)
6.如图,湖心岛上有一凉亭B,在凉亭B的正东湖边有一棵大树A,在湖边的C处测得B在北偏西45°方向上,测得A在北偏东30°方向上,又测得A、C之间的距离为100米,则A、B之间的距离是 米(结果保留根号形式).
7.已知点B位于点A北偏东30°方向,点C位于点A北偏西30°方向,且AB=AC=8千米,那么BC= 千米.
8.为了维护国家主权和海洋权益,海监部门对我领海实施常态化巡航管理.如图,一艘正在执行巡航任务的海监船接到固定监测点P处的值守人员报告;在P处南偏东30°方向上,距离P处14海里的Q处有一可疑船只滞留,海监船以每小时28海里的速度向正东方向航行,在A处测得监测点P在其北偏东60°方向上,继续航行半小时到达了B处,此时测得监测点P在其北偏东30°方向上.
(1)B、P两处间的距离为 海里;如果联结图中的B、Q两点,那么△BPQ是 三角形;如果海监船保持原航向继续航行,那么它 [填“能”或“不能”]到达Q处;
(2)如果监测点P处周围12海里内有暗礁,那么海监船继续向正东方向航行是否安全?
9.如图,已知某船向正东方向航行,在点A处测得某岛C在其北偏东60°方向上,前进8海里后达到点B处,测得岛C在其北偏东45°方向上.已知岛C周围10海里内有暗礁.问:如果该船继续向东航行,有无触礁危险?请说明理由.
10.如图,在东西方向的海岸线l上有长为300米的码头AB,在码头的最西端A处测得轮船M在它的北偏东45°方向上;同一时刻,在A点正东方向距离100米的C处测得轮船M在北偏东22°方向上.
(1)求轮船M到海岸线l的距离;(结果精确到0.01米)
(2)如果轮船M沿着南偏东30°的方向航行,那么该轮船能否行至码头AB靠岸?请说明理由.
(参考数据:sin22°≈0.375,cos22°≈0.927,tan22°≈0.404,≈1.732.)
11.如图,小岛A在港口P的南偏西45°方向上,一艘船从港口P,沿着正南方向,以每小时12海里的速度航行,1小时30分钟后到达B处,在B处测得小岛A在它的南偏西60°的方向上,小岛A离港口P有多少海里?
12.如图,一艘游艇在离开码头A处后,沿南偏西60°方向行驶到达B处,此时从B处发现灯塔C在游轮的东北方向,已知灯塔C在码头A的正西方向200米处,求此时游轮与灯塔C的距离(精确到1米).
(参考数据:=1.414,=1.732,=2.449)
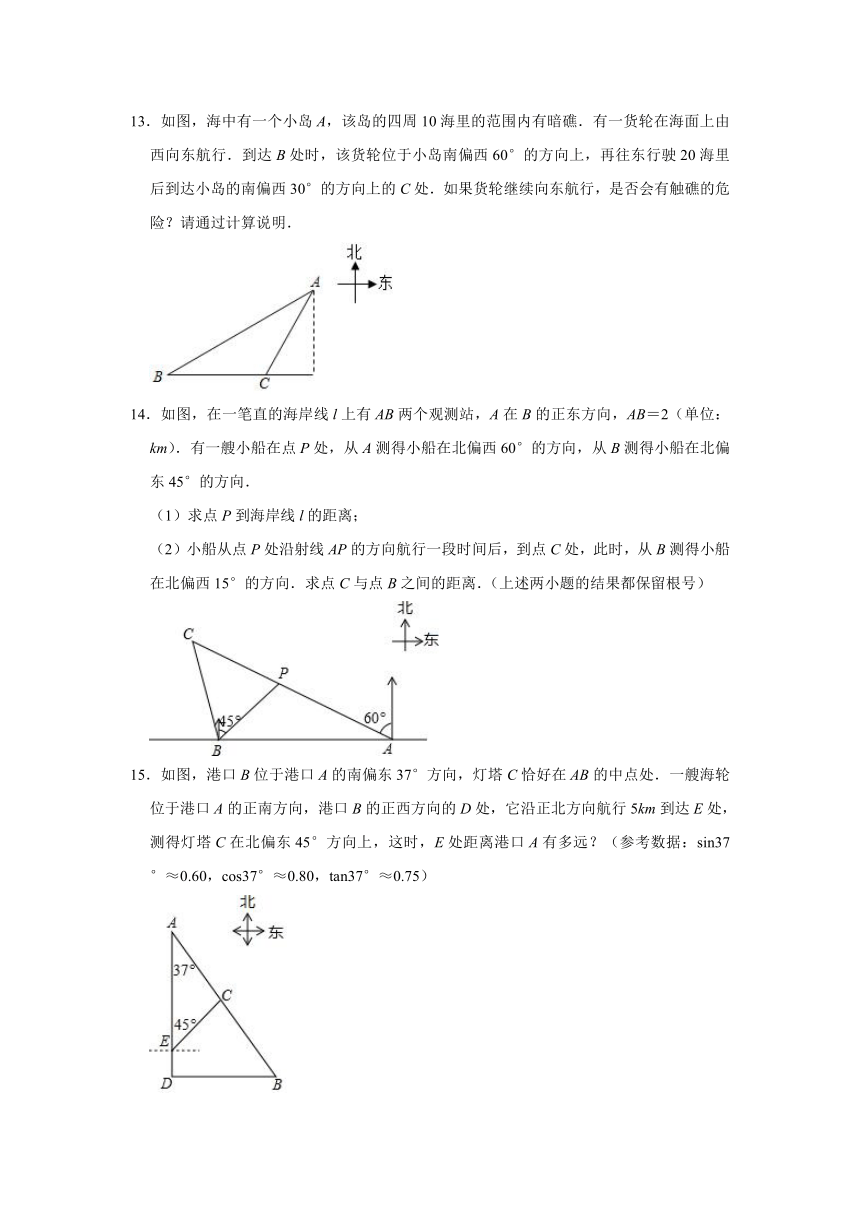
13.如图,海中有一个小岛A,该岛的四周10海里的范围内有暗礁.有一货轮在海面上由西向东航行.到达B处时,该货轮位于小岛南偏西60°的方向上,再往东行驶20海里后到达小岛的南偏西30°的方向上的C处.如果货轮继续向东航行,是否会有触礁的危险?请通过计算说明.
14.如图,在一笔直的海岸线l上有AB两个观测站,A在B的正东方向,AB=2(单位:km).有一艘小船在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向.
(1)求点P到海岸线l的距离;
(2)小船从点P处沿射线AP的方向航行一段时间后,到点C处,此时,从B测得小船在北偏西15°的方向.求点C与点B之间的距离.(上述两小题的结果都保留根号)
15.如图,港口B位于港口A的南偏东37°方向,灯塔C恰好在AB的中点处.一艘海轮位于港口A的正南方向,港口B的正西方向的D处,它沿正北方向航行5km到达E处,测得灯塔C在北偏东45°方向上,这时,E处距离港口A有多远?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
16.“雪龙”号考察船在某海域进行科考活动,在点A处测得小岛C在它的东北方向上,它沿南偏东37°方向航行2海里到达点B处,又测得小岛C在它的北偏东23°方向上(如图所示),求“雪龙”号考察船在点B处与小岛C之间的距离.
(参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,≈1.4,≈1.7)
17.如图,已知某船向正东方向航行,在点A处测得某岛C在其北偏东60°方向上,前进8海里处到达点B处,测得岛C在其北偏东30°方向上.已知岛C周围6海里内有一暗礁,问:如果该船继续向东航行,有无触礁危险?请说明你的理由.
18.如图,在港口A的南偏东37°方向的海面上,有一巡逻艇B,A、B相距20海里,这时在巡逻艇的正北方向及港口A的北偏东67°方向上,有一渔船C发生故障.得知这一情况后,巡逻艇以25海里/小时的速度前往救援,问巡逻艇能否在1小时内到达渔船C处?
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin67°≈,cos67°≈,tan67°≈)
19.温州市处于东南沿海,夏季经常遭受台风袭击,一次,温州气象局测得台风中心在温州市A的正西方向300千米的B处,以每小时10千米的速度向东偏南30°的BC方向移动,距台风中心200千米的范围是受台风严重影响的区域.试问:
(1)台风中心在移动过程中离温州市最近距离是多少千米?
(2)温州市A是否受台风影响?若不会受到,请说明理由;若会受到,求出温州市受台风严重影响的时间.
20.如图,某湖心岛上有一亭子A,在亭子A的正东方向上的湖边有一棵树B,在这个湖心岛的湖边C处测得亭子A在北偏西45°方向上,测得树B在北偏东36°方向上,又测得B、C之间的距离等于200米,求A、B之间的距离
(结果精确到1米).(参考数据:≈1.414,sin36°≈0.588,cos36°≈0.809,tan36°≈0.727,cot36°≈1.376)
21.如图,海中有一个小岛A,该岛四周11海里范围内有暗礁.有一货轮在海面上由西向正东方向航行,到达B处时它在小岛南偏西60°的方向上,再往正东方向行驶10海里后恰好到达小岛南偏西45°方向上的点C处.问:如果货轮继续向正东方向航行,是否会有触礁的危险?
(参考数据:≈1.41,≈1.73)
22.如图,MN是一条东西方向的海岸线,在海岸线上的A处测得一海岛在南偏西32°的方向上,向东走过780米后到达B处,测得海岛在南偏西37°的方向,求小岛到海岸线的距离.
(参考数据:tan37°=cot53°≈0.755,cot37°=tan53°≈1.327,tan32°=cot58°≈0.625,cot32°=tan58°≈1.600.)
23.某条道路上通行车辆的限速60千米/时,道路的AB段为监测区,监测点P到AB的距离PH为50米(如图).已知点P在点A的北偏东45°方向上,且在点B的北偏西60°方向上,点B在点A的北偏东75°方向上,那么车辆通过AB段的时间在多少秒以内,可认定为超速?(参考数据:≈1.7,≈1.4).
参考答案
1.解:如图,
∵BC⊥AE,
∴∠AEB=90°,
∵∠EAB=30°,AB=10千米,
∴BE=5米,AE=5千米,
∴CE=BC﹣BE=20﹣5=15(千米),
∴AC=(千米),
故选:C.
2.解:如图,在Rt△ABC中,∠ABC=90°﹣30°=60°,BC=5海里,
∴AC=BC?tan60°=5(海里),
即海监船C与货轮A的距离是5海里,
故选:B.
3.解:如图所示:
∵小岛B在货船A的北偏东30°方向500米处,
∴货船A在小岛B的南偏西30°方向500米处,
故选:A.
4.解:如图所示:由题意可得,∠PAB=30°,∠DBP=30°,
故∠PBE=60°,
则∠P=∠PAB=30°,
可得:AB=BP=40海里.
故答案为:40.
5.解:如图,作CD⊥AB于点D.
∵在Rt△ACD中,∠CAD=90°﹣60°=30°,
∴CD=AC?sin∠CAD=4×=2(km),AD=AC?cos30°=4×=2(km),
∵Rt△BCD中,∠CDB=90°,∠CBD=45°,
∴BD=CD=2(km),
∴AB=AD+BD=2(km),
故答案是:(2+2).
6.解:如图,过点C作CD⊥AB于点D,
在Rt△ACD中,∵∠ACD=30°,AC=100m,
∴AD=100?sin∠ACD=100×0.5=50(m),
CD=100?cos∠ACD=100×=50(m),
在Rt△BCD中,
∵∠BCD=45°,
∴BD=CD=50m,
则AB=AD+BD=50+50(m),
即A、B之间的距离约为(50+50)米.
故答案为:(50+50).
7.解:依照题意画出图形,如图所示.
(方法一)∵∠BAD=30°,∠CAD=30°,
∴∠BAC=∠BAD+∠CAD=60°.
又∵AB=AC,
∴△ABC为等边三角形,
∴BC=AC=8千米.
故答案为:8.
(方法二)在Rt△ABD中,∠BAD=30°,AB=8千米,
∴BD=4千米.
同理,CD=4千米,
∴BC=BD+CD=8千米.
故答案为:8.
8.解:(1)如图1所示:
由题意得:AB=28×=14(海里),∠PAB=90°﹣60°=30°,∠ABP=90°+30°=120°,
∴∠APB=180°﹣∠PAB﹣∠ABP=30°,∴∠APB=∠PAB,
∴PB=AB=14(海里),
∵BC∥PD,
∴∠BPD=∠PBC=30°,
∴∠BPQ=∠BPD+∠QPD=30°+30°=60°,
∵PQ=PB=14,
∴△BPQ是等边三角形,
∴∠PBQ=60°,
∴∠PBQ+∠ABP=60°+120°=180°,
∴A、B、Q三点共线,
∴如果海监船保持原航向继续航行,那么它到达Q处,
故答案为:14,等边,能;
(2)过点P作PH⊥AB于H,如图2所示:
由(1)得:∠PBH=60°,
在Rt△BHP中,PH=sin60°×PB=×14=7,
∵7>12,
∴海监船继续向正东方向航行是安全的.
9.解:无触礁危险,理由如下:作CD⊥AB于点D,由题意可知,∠CAB=30°,∠CBD=45°,
∴∠ACB=15°,
在Rt△BCD中,
∵∠BDC=90°,∠CBD=45°,
∴∠BCD=45°,
∴BD=CD.
∵AB=8,
∴AD=8+CD=.
∴DC=≈10.9>10,
∴船继续向东航行无触礁危险.
10.解:(1)过点M作MD⊥AC交AC的延长线于D,设DM=x,
∵在Rt△CDM中,CD=DM?tan∠CMD=x?tan22°,
又∵在Rt△ADM中,∠MAC=45°,
∴AD=DM,
∵AD=AC+CD=100+x?tan22°,
∴100+x?tan22°=x,
∴x=≈≈167.79,
答:轮船M到海岸线l的距离约为167.79米.
(2)作∠DMF=30°,交l于点F.
在Rt△DMF中,DF=DM?tan∠FMD=DM?tan30°
=DM≈×167.79≈96.87米,
∴AF=AC+CD+DF=DM+DF≈167.79+96.87=264.66<300,
所以该轮船能行至码头靠岸.
11.解:作AE⊥PB于E,
由题意得,PB=12×1.5=18海里,
设AE=x海里,
∵∠APE=45°,
∴PE=AE=x,
∵∠ABE=60°,
∴BE=x,
由题意得,x﹣x=18,
解得,x=27+9,
则AP=27+9,
答:小岛A离港口P有(27+9)海里.
12.解:过B作BD⊥AC于D,
在Rt△BCD中,∵∠D=90°,∠DBC=45°,
∴∠DBC=∠DCB=45°,
∴BD=CD,
在Rt△ABD中,∵∠DAB=30°,
∴AD=BD,
∵AC=200,
∴BD﹣BD=200,
∴BD==100(+1),
∴BC=BD=100(+1)×≈386米,
答:此时游轮与灯塔C的距离为386米.
13.解:过点A作直线BC的垂线,垂足为D,
由题意,得∠BAD=60°,∠CAD=30°,
∴∠BAC=∠BAD﹣∠CAD=30°,
又∵∠B=90°﹣∠BAD=90°﹣60°=30°,
∴∠B=∠BAC,
∴AC=BC,
∵BC=20,
∴AC=BC=20(海里),
在Rt△ACD中,(海里),
由题意知:以海岛A为圆心,半径长为10海里范围内有暗礁.这里,,
所以,如果货轮继续向东航行,没有触礁的危险.
14.解:(1)如图,过点P作PD⊥AB于点D.设PD=xkm.
在Rt△PBD中,∠BDP=90°,∠PBD=90°﹣45°=45°,
∴BD=PD=xkm.
在Rt△PAD中,∠ADP=90°,∠PAD=90°﹣60°=30°,
∴AD=PD=xkm.
∵BD+AD=AB,
∴x+x=2,
x=﹣1,
∴点P到海岸线l的距离为(﹣1)km;
(2)如图,过点B作BF⊥AC于点F.
根据题意得:∠ABC=105°,
在Rt△ABF中,∠AFB=90°,∠BAF=30°,
∴BF=AB=1km.
在△ABC中,∠C=180°﹣∠BAC﹣∠ABC=45°.
在Rt△BCF中,∠BFC=90°,∠C=45°,
∴BC=BF=km,
∴点C与点B之间的距离为km.
15.解:如图作CH⊥AD于H.设CH=xkm,
在Rt△ACH中,∠A=37°,∵tan37°=,
∴AH==,
在Rt△CEH中,∵∠CEH=45°,
∴CH=EH=x,
∵CH⊥AD,BD⊥AD,
∴CH∥BD,
∴=,
∵AC=CB,
∴AH=HD,
∴=x+5,
∴x=≈15,
∴AE=AH+HE=+15≈35km,
∴E处距离港口A有35km.
16.解:过点A作AM⊥BC,垂足为M.
由题意知:AB=2海里,∠NAC=∠CAE=45°,
∠SAB=37°,∠DBC=23°,
∵∠SAB=37°,DB∥AS,
∴∠DBA=37°,∠EAB=90°﹣∠SAB=53°.
∴∠ABC=∠ABD+∠DBC=37°+23°=60°,
∠CAB=∠EAB+∠CAE=53°+45°=98°.
∴∠C=180°﹣∠CAB﹣∠ABC=180°﹣98°﹣60°=22°.
在Rt△AMB中,∵AB=2海里,∠ABC=60°,
∴BM=1海里,AM=海里.
在Rt△AMC中,tanC=,
∴CM=≈≈=4.25(海里)
∴CB=CM+BM=4.25+1=5.25(海里)
答:“雪龙”号考察船在点B处与小岛C之间的距离为5.25海里.
17.解:作CD⊥AB于点D,由题意可知,∠CAB=30°,∠CBD=60°,
∴∠ACB=30°,
在Rt△BCD中,
∵∠BDC=90°,∠CBD=60°,
∴∠BCD=30°,
∴∠ACB=∠BCD.
∴△CDB∽△ADC.
∴=
∵AB=CB=8
∴BD=4,AD=12.
∴=
∴CD=4
≈6.928>6.
∴船继续向东航行无触礁危险.
18.解:过点A作AH⊥BC,垂足为点H.
由题意,得∠ACH=67°,∠B=37°,AB=20.
在Rt△ABH中,
∵sinB=,∴AH=AB?sin∠B=20×sin37°≈12,
∵cosB=,∴BH=AB?cos∠B=20×cos37°≈16,
在Rt△ACH中,
∵tan∠ACH=,
∴CH=≈5,
∵BC=BH+CH,∴BC≈16+5=21.
∵21÷25<1,
所以,巡逻艇能在1小时内到达渔船C处.
19.解:(1)过点A作AD⊥BC于D,
由题意得AB=300,∠ABD=30°
∴AD=AB=150(km);(3分)
(2)∵150<200
∴温州市点A受到台风严重影响
设台风中心距A点200km处,
刚好处在BC上的E,F两点则
在Rt△ADE中,AE=200,AD=150
∴DE==
∴EF=2DE=
∴温州市A受台风严重影响的时间为.(6分)
20.解:过点C作CH⊥AB,垂足为点H,
由题意,得∠ACH=45°,∠BCH=36°,BC=200,
在Rt△BHC中,,
∴,
∵sin36°≈0.588,
∴BH≈117.6,
又,
∴.
∵cos36°≈0.809,
∴HC≈161.8,
在Rt△AHC中,,
∵∠ACH=45°,
∴AH=HC,
∴AH≈161.8,
又AB=AH+BH,
∴AB≈279.4,
∴AB≈279(米),
答:A、B之间的距离为279米.
21.解:过点A作AH⊥BC,垂足为点H.
由题意,得∠BAH=60°,∠CAH=45°,BC=10.(
设AH=x,则CH=x.
在Rt△ABH中,
∵,
∴,
∴,
解得,
∵13.65>11,
∴货轮继续向正东方向航行,不会有触礁的危险.
22.解:过点C作CD⊥MN,垂足为D,设CD=x米,
∵AB=BD﹣AD,
∴xtan37°﹣xtan32°=780,
解得:x=6000,
答:小岛到海岸线的距离6000米.
23.解:如图,由题意知∠CAB=75°、∠CAP=45°、∠PBD=60°,
∴∠PAH=∠CAB﹣∠CAP=30°,
∵∠PHA=∠PHB=90°,PH=50,
∴AH===50,
∵AC∥BD,
∴∠ABD=180°﹣∠CAB=105°,
∴∠PBH=∠ABD﹣∠PBD=45°,
则PH=BH=50,
∴AB=AH+BH=50+50,
∵60千米/时=米/秒,
∴时间t==3+3≈8.1(秒),
即车辆通过AB段的时间在8.1秒以内,可认定为超速
1.如图,一艘船从A处向北偏东30°的方向行驶10千米到B处,再从B处向正西方向行驶20千米到C处,这时这艘船与A的距离( )
A.15千米 B.10千米 C.10千米 D.5千米
2.已知海面上一艘货轮A在灯塔B的北偏东30°方向,海监船C在灯塔B的正东方向5海里处,此时海监船C发现货轮A在它的正北方向,那么海监船C与货轮A的距离是( )A.10海里 B.5海里 C.5海里 D.海里
3.如果从货船A测得小岛b在货船A的北偏东30°方向500米处,那么从小岛B看货船A的位置,此时货船A在小岛B的( )
A.南偏西30°方向500米处 B.南偏西60°方向500米处
C.南偏西30°方向250米处 D.南偏西60°方向250米处
4.如图,一艘轮船由西向东航行,在A处测得灯塔P在北偏东60°的方向,继续向东航行40海里后到B处,测得灯塔P在北偏东30°的方向,此时轮船与灯塔之间的距离是 海里.
5.如图,在一条东西方向笔直的沿湖道路l上有A、B两个游船码头,观光岛屿C在码头A的北偏东60°方向、在码头B的北偏西45°方向,AC=4千米.那么码头A、B之间的距离等于 千米.(结果保留根号)
6.如图,湖心岛上有一凉亭B,在凉亭B的正东湖边有一棵大树A,在湖边的C处测得B在北偏西45°方向上,测得A在北偏东30°方向上,又测得A、C之间的距离为100米,则A、B之间的距离是 米(结果保留根号形式).
7.已知点B位于点A北偏东30°方向,点C位于点A北偏西30°方向,且AB=AC=8千米,那么BC= 千米.
8.为了维护国家主权和海洋权益,海监部门对我领海实施常态化巡航管理.如图,一艘正在执行巡航任务的海监船接到固定监测点P处的值守人员报告;在P处南偏东30°方向上,距离P处14海里的Q处有一可疑船只滞留,海监船以每小时28海里的速度向正东方向航行,在A处测得监测点P在其北偏东60°方向上,继续航行半小时到达了B处,此时测得监测点P在其北偏东30°方向上.
(1)B、P两处间的距离为 海里;如果联结图中的B、Q两点,那么△BPQ是 三角形;如果海监船保持原航向继续航行,那么它 [填“能”或“不能”]到达Q处;
(2)如果监测点P处周围12海里内有暗礁,那么海监船继续向正东方向航行是否安全?
9.如图,已知某船向正东方向航行,在点A处测得某岛C在其北偏东60°方向上,前进8海里后达到点B处,测得岛C在其北偏东45°方向上.已知岛C周围10海里内有暗礁.问:如果该船继续向东航行,有无触礁危险?请说明理由.
10.如图,在东西方向的海岸线l上有长为300米的码头AB,在码头的最西端A处测得轮船M在它的北偏东45°方向上;同一时刻,在A点正东方向距离100米的C处测得轮船M在北偏东22°方向上.
(1)求轮船M到海岸线l的距离;(结果精确到0.01米)
(2)如果轮船M沿着南偏东30°的方向航行,那么该轮船能否行至码头AB靠岸?请说明理由.
(参考数据:sin22°≈0.375,cos22°≈0.927,tan22°≈0.404,≈1.732.)
11.如图,小岛A在港口P的南偏西45°方向上,一艘船从港口P,沿着正南方向,以每小时12海里的速度航行,1小时30分钟后到达B处,在B处测得小岛A在它的南偏西60°的方向上,小岛A离港口P有多少海里?
12.如图,一艘游艇在离开码头A处后,沿南偏西60°方向行驶到达B处,此时从B处发现灯塔C在游轮的东北方向,已知灯塔C在码头A的正西方向200米处,求此时游轮与灯塔C的距离(精确到1米).
(参考数据:=1.414,=1.732,=2.449)
13.如图,海中有一个小岛A,该岛的四周10海里的范围内有暗礁.有一货轮在海面上由西向东航行.到达B处时,该货轮位于小岛南偏西60°的方向上,再往东行驶20海里后到达小岛的南偏西30°的方向上的C处.如果货轮继续向东航行,是否会有触礁的危险?请通过计算说明.
14.如图,在一笔直的海岸线l上有AB两个观测站,A在B的正东方向,AB=2(单位:km).有一艘小船在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向.
(1)求点P到海岸线l的距离;
(2)小船从点P处沿射线AP的方向航行一段时间后,到点C处,此时,从B测得小船在北偏西15°的方向.求点C与点B之间的距离.(上述两小题的结果都保留根号)
15.如图,港口B位于港口A的南偏东37°方向,灯塔C恰好在AB的中点处.一艘海轮位于港口A的正南方向,港口B的正西方向的D处,它沿正北方向航行5km到达E处,测得灯塔C在北偏东45°方向上,这时,E处距离港口A有多远?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
16.“雪龙”号考察船在某海域进行科考活动,在点A处测得小岛C在它的东北方向上,它沿南偏东37°方向航行2海里到达点B处,又测得小岛C在它的北偏东23°方向上(如图所示),求“雪龙”号考察船在点B处与小岛C之间的距离.
(参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,≈1.4,≈1.7)
17.如图,已知某船向正东方向航行,在点A处测得某岛C在其北偏东60°方向上,前进8海里处到达点B处,测得岛C在其北偏东30°方向上.已知岛C周围6海里内有一暗礁,问:如果该船继续向东航行,有无触礁危险?请说明你的理由.
18.如图,在港口A的南偏东37°方向的海面上,有一巡逻艇B,A、B相距20海里,这时在巡逻艇的正北方向及港口A的北偏东67°方向上,有一渔船C发生故障.得知这一情况后,巡逻艇以25海里/小时的速度前往救援,问巡逻艇能否在1小时内到达渔船C处?
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin67°≈,cos67°≈,tan67°≈)
19.温州市处于东南沿海,夏季经常遭受台风袭击,一次,温州气象局测得台风中心在温州市A的正西方向300千米的B处,以每小时10千米的速度向东偏南30°的BC方向移动,距台风中心200千米的范围是受台风严重影响的区域.试问:
(1)台风中心在移动过程中离温州市最近距离是多少千米?
(2)温州市A是否受台风影响?若不会受到,请说明理由;若会受到,求出温州市受台风严重影响的时间.
20.如图,某湖心岛上有一亭子A,在亭子A的正东方向上的湖边有一棵树B,在这个湖心岛的湖边C处测得亭子A在北偏西45°方向上,测得树B在北偏东36°方向上,又测得B、C之间的距离等于200米,求A、B之间的距离
(结果精确到1米).(参考数据:≈1.414,sin36°≈0.588,cos36°≈0.809,tan36°≈0.727,cot36°≈1.376)
21.如图,海中有一个小岛A,该岛四周11海里范围内有暗礁.有一货轮在海面上由西向正东方向航行,到达B处时它在小岛南偏西60°的方向上,再往正东方向行驶10海里后恰好到达小岛南偏西45°方向上的点C处.问:如果货轮继续向正东方向航行,是否会有触礁的危险?
(参考数据:≈1.41,≈1.73)
22.如图,MN是一条东西方向的海岸线,在海岸线上的A处测得一海岛在南偏西32°的方向上,向东走过780米后到达B处,测得海岛在南偏西37°的方向,求小岛到海岸线的距离.
(参考数据:tan37°=cot53°≈0.755,cot37°=tan53°≈1.327,tan32°=cot58°≈0.625,cot32°=tan58°≈1.600.)
23.某条道路上通行车辆的限速60千米/时,道路的AB段为监测区,监测点P到AB的距离PH为50米(如图).已知点P在点A的北偏东45°方向上,且在点B的北偏西60°方向上,点B在点A的北偏东75°方向上,那么车辆通过AB段的时间在多少秒以内,可认定为超速?(参考数据:≈1.7,≈1.4).
参考答案
1.解:如图,
∵BC⊥AE,
∴∠AEB=90°,
∵∠EAB=30°,AB=10千米,
∴BE=5米,AE=5千米,
∴CE=BC﹣BE=20﹣5=15(千米),
∴AC=(千米),
故选:C.
2.解:如图,在Rt△ABC中,∠ABC=90°﹣30°=60°,BC=5海里,
∴AC=BC?tan60°=5(海里),
即海监船C与货轮A的距离是5海里,
故选:B.
3.解:如图所示:
∵小岛B在货船A的北偏东30°方向500米处,
∴货船A在小岛B的南偏西30°方向500米处,
故选:A.
4.解:如图所示:由题意可得,∠PAB=30°,∠DBP=30°,
故∠PBE=60°,
则∠P=∠PAB=30°,
可得:AB=BP=40海里.
故答案为:40.
5.解:如图,作CD⊥AB于点D.
∵在Rt△ACD中,∠CAD=90°﹣60°=30°,
∴CD=AC?sin∠CAD=4×=2(km),AD=AC?cos30°=4×=2(km),
∵Rt△BCD中,∠CDB=90°,∠CBD=45°,
∴BD=CD=2(km),
∴AB=AD+BD=2(km),
故答案是:(2+2).
6.解:如图,过点C作CD⊥AB于点D,
在Rt△ACD中,∵∠ACD=30°,AC=100m,
∴AD=100?sin∠ACD=100×0.5=50(m),
CD=100?cos∠ACD=100×=50(m),
在Rt△BCD中,
∵∠BCD=45°,
∴BD=CD=50m,
则AB=AD+BD=50+50(m),
即A、B之间的距离约为(50+50)米.
故答案为:(50+50).
7.解:依照题意画出图形,如图所示.
(方法一)∵∠BAD=30°,∠CAD=30°,
∴∠BAC=∠BAD+∠CAD=60°.
又∵AB=AC,
∴△ABC为等边三角形,
∴BC=AC=8千米.
故答案为:8.
(方法二)在Rt△ABD中,∠BAD=30°,AB=8千米,
∴BD=4千米.
同理,CD=4千米,
∴BC=BD+CD=8千米.
故答案为:8.
8.解:(1)如图1所示:
由题意得:AB=28×=14(海里),∠PAB=90°﹣60°=30°,∠ABP=90°+30°=120°,
∴∠APB=180°﹣∠PAB﹣∠ABP=30°,∴∠APB=∠PAB,
∴PB=AB=14(海里),
∵BC∥PD,
∴∠BPD=∠PBC=30°,
∴∠BPQ=∠BPD+∠QPD=30°+30°=60°,
∵PQ=PB=14,
∴△BPQ是等边三角形,
∴∠PBQ=60°,
∴∠PBQ+∠ABP=60°+120°=180°,
∴A、B、Q三点共线,
∴如果海监船保持原航向继续航行,那么它到达Q处,
故答案为:14,等边,能;
(2)过点P作PH⊥AB于H,如图2所示:
由(1)得:∠PBH=60°,
在Rt△BHP中,PH=sin60°×PB=×14=7,
∵7>12,
∴海监船继续向正东方向航行是安全的.
9.解:无触礁危险,理由如下:作CD⊥AB于点D,由题意可知,∠CAB=30°,∠CBD=45°,
∴∠ACB=15°,
在Rt△BCD中,
∵∠BDC=90°,∠CBD=45°,
∴∠BCD=45°,
∴BD=CD.
∵AB=8,
∴AD=8+CD=.
∴DC=≈10.9>10,
∴船继续向东航行无触礁危险.
10.解:(1)过点M作MD⊥AC交AC的延长线于D,设DM=x,
∵在Rt△CDM中,CD=DM?tan∠CMD=x?tan22°,
又∵在Rt△ADM中,∠MAC=45°,
∴AD=DM,
∵AD=AC+CD=100+x?tan22°,
∴100+x?tan22°=x,
∴x=≈≈167.79,
答:轮船M到海岸线l的距离约为167.79米.
(2)作∠DMF=30°,交l于点F.
在Rt△DMF中,DF=DM?tan∠FMD=DM?tan30°
=DM≈×167.79≈96.87米,
∴AF=AC+CD+DF=DM+DF≈167.79+96.87=264.66<300,
所以该轮船能行至码头靠岸.
11.解:作AE⊥PB于E,
由题意得,PB=12×1.5=18海里,
设AE=x海里,
∵∠APE=45°,
∴PE=AE=x,
∵∠ABE=60°,
∴BE=x,
由题意得,x﹣x=18,
解得,x=27+9,
则AP=27+9,
答:小岛A离港口P有(27+9)海里.
12.解:过B作BD⊥AC于D,
在Rt△BCD中,∵∠D=90°,∠DBC=45°,
∴∠DBC=∠DCB=45°,
∴BD=CD,
在Rt△ABD中,∵∠DAB=30°,
∴AD=BD,
∵AC=200,
∴BD﹣BD=200,
∴BD==100(+1),
∴BC=BD=100(+1)×≈386米,
答:此时游轮与灯塔C的距离为386米.
13.解:过点A作直线BC的垂线,垂足为D,
由题意,得∠BAD=60°,∠CAD=30°,
∴∠BAC=∠BAD﹣∠CAD=30°,
又∵∠B=90°﹣∠BAD=90°﹣60°=30°,
∴∠B=∠BAC,
∴AC=BC,
∵BC=20,
∴AC=BC=20(海里),
在Rt△ACD中,(海里),
由题意知:以海岛A为圆心,半径长为10海里范围内有暗礁.这里,,
所以,如果货轮继续向东航行,没有触礁的危险.
14.解:(1)如图,过点P作PD⊥AB于点D.设PD=xkm.
在Rt△PBD中,∠BDP=90°,∠PBD=90°﹣45°=45°,
∴BD=PD=xkm.
在Rt△PAD中,∠ADP=90°,∠PAD=90°﹣60°=30°,
∴AD=PD=xkm.
∵BD+AD=AB,
∴x+x=2,
x=﹣1,
∴点P到海岸线l的距离为(﹣1)km;
(2)如图,过点B作BF⊥AC于点F.
根据题意得:∠ABC=105°,
在Rt△ABF中,∠AFB=90°,∠BAF=30°,
∴BF=AB=1km.
在△ABC中,∠C=180°﹣∠BAC﹣∠ABC=45°.
在Rt△BCF中,∠BFC=90°,∠C=45°,
∴BC=BF=km,
∴点C与点B之间的距离为km.
15.解:如图作CH⊥AD于H.设CH=xkm,
在Rt△ACH中,∠A=37°,∵tan37°=,
∴AH==,
在Rt△CEH中,∵∠CEH=45°,
∴CH=EH=x,
∵CH⊥AD,BD⊥AD,
∴CH∥BD,
∴=,
∵AC=CB,
∴AH=HD,
∴=x+5,
∴x=≈15,
∴AE=AH+HE=+15≈35km,
∴E处距离港口A有35km.
16.解:过点A作AM⊥BC,垂足为M.
由题意知:AB=2海里,∠NAC=∠CAE=45°,
∠SAB=37°,∠DBC=23°,
∵∠SAB=37°,DB∥AS,
∴∠DBA=37°,∠EAB=90°﹣∠SAB=53°.
∴∠ABC=∠ABD+∠DBC=37°+23°=60°,
∠CAB=∠EAB+∠CAE=53°+45°=98°.
∴∠C=180°﹣∠CAB﹣∠ABC=180°﹣98°﹣60°=22°.
在Rt△AMB中,∵AB=2海里,∠ABC=60°,
∴BM=1海里,AM=海里.
在Rt△AMC中,tanC=,
∴CM=≈≈=4.25(海里)
∴CB=CM+BM=4.25+1=5.25(海里)
答:“雪龙”号考察船在点B处与小岛C之间的距离为5.25海里.
17.解:作CD⊥AB于点D,由题意可知,∠CAB=30°,∠CBD=60°,
∴∠ACB=30°,
在Rt△BCD中,
∵∠BDC=90°,∠CBD=60°,
∴∠BCD=30°,
∴∠ACB=∠BCD.
∴△CDB∽△ADC.
∴=
∵AB=CB=8
∴BD=4,AD=12.
∴=
∴CD=4
≈6.928>6.
∴船继续向东航行无触礁危险.
18.解:过点A作AH⊥BC,垂足为点H.
由题意,得∠ACH=67°,∠B=37°,AB=20.
在Rt△ABH中,
∵sinB=,∴AH=AB?sin∠B=20×sin37°≈12,
∵cosB=,∴BH=AB?cos∠B=20×cos37°≈16,
在Rt△ACH中,
∵tan∠ACH=,
∴CH=≈5,
∵BC=BH+CH,∴BC≈16+5=21.
∵21÷25<1,
所以,巡逻艇能在1小时内到达渔船C处.
19.解:(1)过点A作AD⊥BC于D,
由题意得AB=300,∠ABD=30°
∴AD=AB=150(km);(3分)
(2)∵150<200
∴温州市点A受到台风严重影响
设台风中心距A点200km处,
刚好处在BC上的E,F两点则
在Rt△ADE中,AE=200,AD=150
∴DE==
∴EF=2DE=
∴温州市A受台风严重影响的时间为.(6分)
20.解:过点C作CH⊥AB,垂足为点H,
由题意,得∠ACH=45°,∠BCH=36°,BC=200,
在Rt△BHC中,,
∴,
∵sin36°≈0.588,
∴BH≈117.6,
又,
∴.
∵cos36°≈0.809,
∴HC≈161.8,
在Rt△AHC中,,
∵∠ACH=45°,
∴AH=HC,
∴AH≈161.8,
又AB=AH+BH,
∴AB≈279.4,
∴AB≈279(米),
答:A、B之间的距离为279米.
21.解:过点A作AH⊥BC,垂足为点H.
由题意,得∠BAH=60°,∠CAH=45°,BC=10.(
设AH=x,则CH=x.
在Rt△ABH中,
∵,
∴,
∴,
解得,
∵13.65>11,
∴货轮继续向正东方向航行,不会有触礁的危险.
22.解:过点C作CD⊥MN,垂足为D,设CD=x米,
∵AB=BD﹣AD,
∴xtan37°﹣xtan32°=780,
解得:x=6000,
答:小岛到海岸线的距离6000米.
23.解:如图,由题意知∠CAB=75°、∠CAP=45°、∠PBD=60°,
∴∠PAH=∠CAB﹣∠CAP=30°,
∵∠PHA=∠PHB=90°,PH=50,
∴AH===50,
∵AC∥BD,
∴∠ABD=180°﹣∠CAB=105°,
∴∠PBH=∠ABD﹣∠PBD=45°,
则PH=BH=50,
∴AB=AH+BH=50+50,
∵60千米/时=米/秒,
∴时间t==3+3≈8.1(秒),
即车辆通过AB段的时间在8.1秒以内,可认定为超速
