2.4解直角三角形同步训练(附答案)-2021--2022学年鲁教版(五四制)九年级数学上册
文档属性
| 名称 | 2.4解直角三角形同步训练(附答案)-2021--2022学年鲁教版(五四制)九年级数学上册 |
|
|
| 格式 | doc | ||
| 文件大小 | 303.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-31 00:00:00 | ||
图片预览



文档简介
2021年鲁教版九年级数学上册《2.4解直角三角形》同步优生辅导训练(附答案)
一.选择题(共12小题)
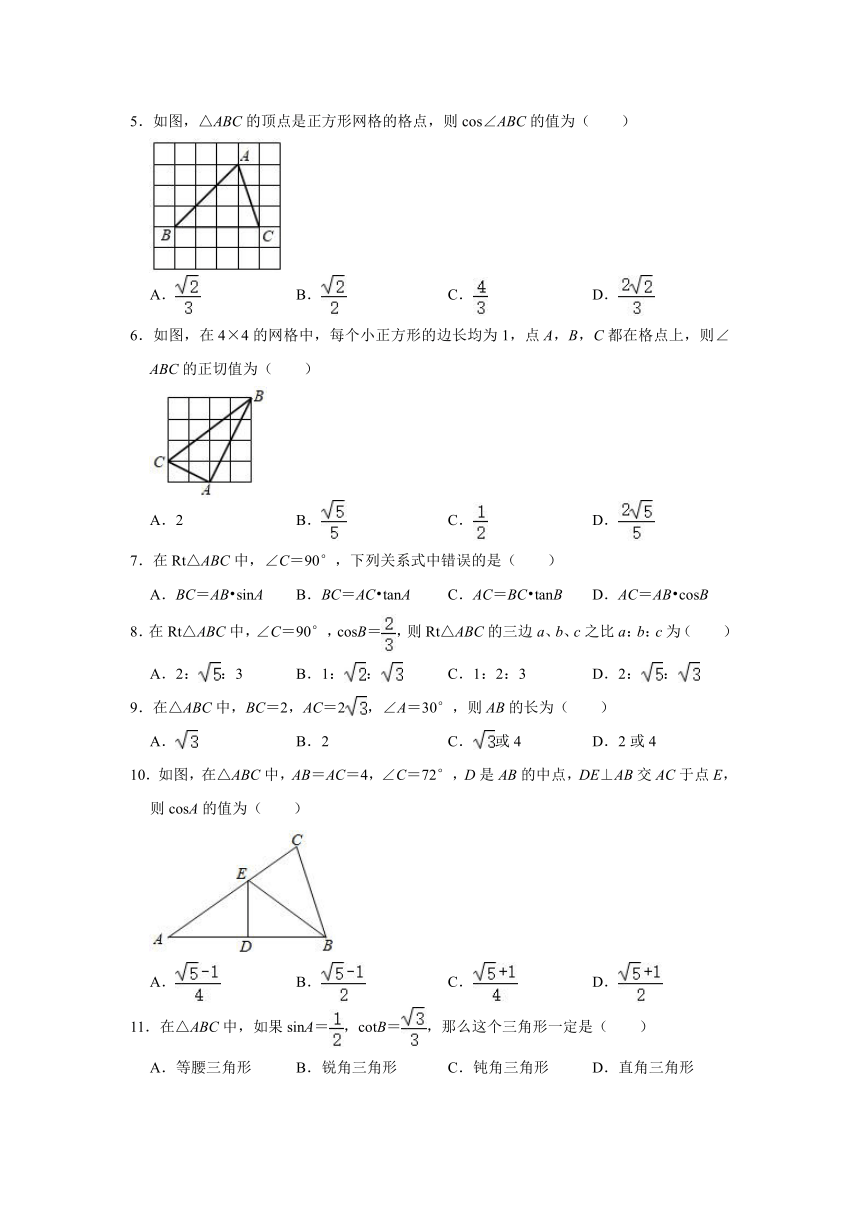
1.如图,在△ABC中,∠ABC=90°,tan∠BAC=,AD=2,BD=4,连接CD,则CD长的最大值是( )
A.2+ B.2+1 C.2+ D.2+2
2.如图,在△ABC中,点O是角平分线AD、BE的交点,若AB=AC=10,BC=12,则tan∠OBD的值是( )
A. B.2 C. D.
3.如图,△ABC底边BC上的高为h1,△PQR底边QR上的高为h2,则有( )
A.h1=h2 B.h1<h2
C.h1>h2 D.以上都有可能
4.如图,已知在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足是D,设∠CAB=α,CD=h,那么BC的长度为( )
A. B. C. D.h?cosα
5.如图,△ABC的顶点是正方形网格的格点,则cos∠ABC的值为( )
A. B. C. D.
6.如图,在4×4的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值为( )
A.2 B. C. D.
7.在Rt△ABC中,∠C=90°,下列关系式中错误的是( )
A.BC=AB?sinA B.BC=AC?tanA C.AC=BC?tanB D.AC=AB?cosB
8.在Rt△ABC中,∠C=90°,cosB=,则Rt△ABC的三边a、b、c之比a:b:c为( )
A.2::3 B.1:: C.1:2:3 D.2::
9.在△ABC中,BC=2,AC=2,∠A=30°,则AB的长为( )
A. B.2 C.或4 D.2或4
10.如图,在△ABC中,AB=AC=4,∠C=72°,D是AB的中点,DE⊥AB交AC于点E,则cosA的值为( )
A. B. C. D.
11.在△ABC中,如果sinA=,cotB=,那么这个三角形一定是( )
A.等腰三角形 B.锐角三角形 C.钝角三角形 D.直角三角形
12.如图,已知∠ABC=60°,BD是∠ABC的平分线,BE是∠CBD的平分线,O,P分别是BD,BE上的动点(与点B不重合),分别过点O,P作OM⊥BC,PN⊥BC,垂足分别是点M,N.当点M,N重合时,的值是( )
A.+1 B.2﹣3 C.2 D.
二.填空题(共4小题)
13.将一副直角三角板拼成如图所示的四边形ABCD,一边重合,若∠CAB=45°,∠CAD=30°,连接BD,则tan∠DBC= .
14.如图△ABC中∠ACB=90°,D在AC上,AD=4CD,若∠BAC=2∠CBD,则tanA= .
15.在Rt△ABC中,∠C=90°,sinB=,若斜边上的高CD=2,则AC= .
16.在△ABC中,AB=2AC,tanB=,BC边上的高长为2,则△ABC的面积为 .
三.解答题(共4小题)
17.如图,在Rt△ABC中,∠A=90°,作BC的垂直平分线交AC于点D,延长AC至点E,使CE=AB.
(1)若AE=1,求△ABD的周长;
(2)若AD=BD,求tan∠ABC的值.
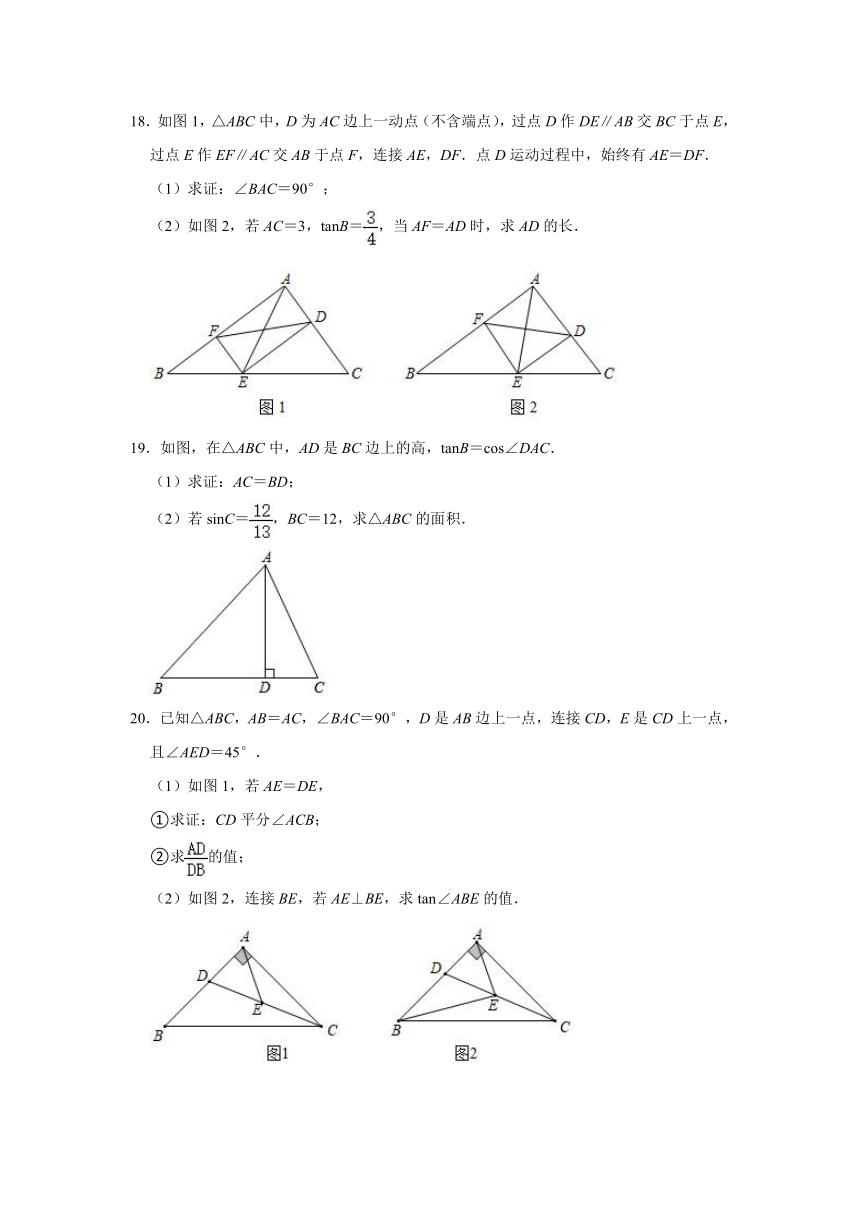
18.如图1,△ABC中,D为AC边上一动点(不含端点),过点D作DE∥AB交BC于点E,过点E作EF∥AC交AB于点F,连接AE,DF.点D运动过程中,始终有AE=DF.
(1)求证:∠BAC=90°;
(2)如图2,若AC=3,tanB=,当AF=AD时,求AD的长.
19.如图,在△ABC中,AD是BC边上的高,tanB=cos∠DAC.
(1)求证:AC=BD;
(2)若sinC=,BC=12,求△ABC的面积.
20.已知△ABC,AB=AC,∠BAC=90°,D是AB边上一点,连接CD,E是CD上一点,且∠AED=45°.
(1)如图1,若AE=DE,
①求证:CD平分∠ACB;
②求的值;
(2)如图2,连接BE,若AE⊥BE,求tan∠ABE的值.
参考答案
一.选择题(共12小题)
1.解:如图,在AD的下方作Rt△ADT,使得∠ADT=90°,DT=1,连接CT,则AT=,
∵==2,
∴=,
∵∠ADT=∠ABC=90°,
∴△ADT∽△ABC,
∴∠DAT=∠BAC,=
∴∠DAB=∠TAC,
∵=,
∴△DAB∽△TAC,
∴==,
∴TC=2,
∵CD≤DT+CT,
∴CD≤1+2,
∴CD的最大值为1+2,
故选:B.
2.解:如图:
作OF⊥AB于F,
∵AB=AC,AD平分∠BAC.
∴∠ODB=90°.BD=CD=6.
∴根据勾股定理得:AD==8.
∵BE平分∠ABC.
∴OF=OD,BF=BD=6,AF=10﹣6=4.
设OD=OF=x,则AO=8﹣x,在Rt△AOF中,根据勾股定理得:
(8﹣x)2=x2+42.
∴x=3.
∴OD=3.
在Rt△OBD中,tan∠OBD===.
故选:A.
3.解:如图,分别作出△ABC底边BC上的高为AD即h1,△PQR底边QR上的高为PE即h2,
在Rt△ADC中,h1=AD=5×sin55°,
在Rt△PER中,h2=PE=5×sin55°,
∴h1=h2,
故选:A.
4.解:∵CD⊥AB,
∴∠CAD+∠DCA=90°,
∵∠ACB=∠ACD+∠BCD=90°,
∴∠BCD=∠CAD=α,
在Rt△BCD中,
∵cos∠BCD=,CD=h,
∴BC=.
故选:B.
5.解:法一、如图,
在Rt△ABD中,∠ADB=90°,AD=BD=3,
∴AB===3,
∴cos∠ABC===.
故选:B.
法二、在Rt△ABD中,∠ADB=90°,AD=BD=3,
∴∠ABD=∠BAD=45°,
∴cos∠ABC=cos45°=.
故选:B.
6.解:∵AC2=12+22=5,
AB2=22+42=20,
BC2=32+42=25,
∴AC2+AB2=BC2.
∴∠CAB=90°.
∴tan∠ABC=.
故选:C.
7.解:如图所示:
∵sinA=,∴BC=sinA×AB,故选项A正确;
∵tanA=,∴BC=tanA×AC,故选项B正确;
∵tanB=,∴AC=tanB×BC,故选项C正确;
∵cosB=,∴BC=cosB×AB≠AC,故选项D错误.
故选:D.
8.解:∵∠C=90°,
∴cosB==,
设a=2x,c=3x,
∴b==x,
∴a:b:c=2x:x:3x=2::3.
故选:A.
9.解:作CD⊥AB交AB的延长线于点D,
当B2C=2时,
∵∠A=30°,∠ADC=90°,AC=2,
∴CD=,
∴AD==3,B2D==1,
∴AB2=3﹣1=2,
同理可得,AB1=3+1=4,
即AB的长为2或4,
故选:D.
10.解:∵在△ABC中,AB=AC=4,∠C=72°,
∴∠ABC=∠C=72°,∠A=180°﹣∠C﹣∠ABC=36°.
∵D是AB中点,DE⊥AB,
∴AE=BE,AD=BD=AB=2,
∴∠ABE=∠A=36°,
∴∠BEC=∠A+∠ABE=72°=∠C,
∴BE=BC=AE,
设BC=AE=x,则CE=AC﹣AE=4﹣x.
∵∠ABC=∠BEC,∠C=∠C,
∴△ABC∽△BEC,
∴=,
即=,
解得:x1=2﹣2,x2=﹣2﹣2(舍去),
∴AE=2﹣2,
∴cosA===,
故选:C.
11.解:∵sinA=,cotB=,
∴∠A=30°,∠B=60°,
∴∠C=180°﹣30°﹣60°=90°,
∴△ABC是直角三角形,
故选:D.
12.解:当M,N重合时,点P在OM上,如图,过点P作PH⊥BD于H,
∵BE是∠CBD的平分线,PN⊥BC,
∴PH=PM,
∵∠ABC=60°,BD是∠ABC的平分线,
∴∠CBD=∠ABC=30°,
∴∠BOP=90°﹣30°=60°,
∵在Rt△POH中,
PO==PH,
∴=+1.
故选:A.
二.填空题(共4小题)
13.解:作DE⊥BC,交BC延长线于点E,设CD=x,
∵∠CAB=45°,∠CAD=30°,一副直角三角板拼成的四边形ABCD,
∴∠ACB=90°,∠ADC=90°,
∴∠DCE=30°,
∴BC=AC=2x,DE=x,CE=x,
∴tan∠DBC===.
故答案为:.
14.解:延长AC至E,使CE=CD,连接BE,
∵∠ACB=90°,
∴BC⊥AC,
∵CE=CD,
∴BC是DE的垂直平分线,
∴BD=BE,
∴∠E=∠BDE,
设∠CBD=α,则∠BAC=2α,
∴∠E=∠BDE=90°﹣α,
∴∠ABE=180°﹣∠E﹣BAC=180°﹣(90°﹣α)﹣2α=90°﹣α,
∴∠E=∠ABE,
∴AB=AE,
设CD=x,则AD=4x,
∴AE=AB=6x,AC=5x,
在Rt△ABC中,BC===x,
∴tanA==.
故答案为:.
15.解:在Rt△ABC中,∠C=90°,
∴∠A+∠B=90°.
∵CD⊥AB,
∴∠A+∠ACD=90°.
∴∠ACD=∠B.
∵sinB=,
∴sin∠ACD=.
∵sin∠BCD=.
∴=.
设AD=a,则AC=3a.
.
∵CD=2,
∴2.
∴a=.
∴AC=.
故答案为:.
16.解:在Rt△ADB中,tanB=,
∴=,
解得,BD=6,
由勾股定理得,AB===2,
∴AC===,
由勾股定理得,CD===1,
如图1,BC=CD+BD=1+6=7,
∴△ABC的面积=×BC×AD=×7×2=7,
如图2,BC=BD﹣CD=6﹣1=5,
∴△ABC的面积=×BC×AD=×5×2=5,
∴△ABC的面积为7或5,
故答案为:7或5.
三.解答题(共4小题)
17.解:(1)如图,连接BD,设BC垂直平分线交BC于点F,
∴BD=CD,
C△ABD=AB+AD+BD
=AB+AD+DC
=AB+AC,
∵AB=CE,
∴C△ABD=AC+CE=AE=1,
故△ABD的周长为1.
(2)设AD=x,
∴BD=3x,
又∵BD=CD,
∴AC=AD+CD=4x,
在Rt△ABD中,AB===2.
∴tan∠ABC===.
18.(1)证明:∵DE∥AB,EF∥AC,
∴四边形ADEF是平行四边形.
∵AE=DF,
∴?ADEF是矩形.
∴∠BAC=90°.
(2)解:当AF=AD时,
由(1)知,此时四边形ADEF是正方形.
方法1,
∵DE∥AB,
∴∠DEC=∠B,∠EDC=∠BAC=90°.
∴tan∠DEC=tanB=.
在Rt△DEC中,设DC=3x,则DE=4x.
∵四边形ADEF是正方形,
∴AD=DE=4x.
∴AC=AD+DC=7x=3.
∴x=,
∴AD=4x=.
方法2:
在Rt△ABC中,∠BAC=90°,tanB=,AC=3,
∴AB=4.
∵四边形ADEF是正方形,设AD=DE=x.
∵DE∥AB,
∴△CED∽△CBA.
∴,
即,
解得x=,
∴AD=.
19.(1)证明:∵AD是BC边上的高,
∴∠ADB=∠ADC=90°,
∵tanB=cos∠DAC,
∴=,
∴BD=AC;
(2)解:设AC=BD=x,
∴CD=BC﹣BD=12﹣x,
∵sinC=,
∴cosC=,tanC=,
∴=,=,
即=,
解得:x=,
∴CD=12﹣x=,
∴AD=CD=×=8,
∴△ABC的面积=BC×AD=×12×8=48.
20.(1)①证明:∵AE=DE,
∴∠ADE=∠DAE,
∵∠CAD=90°,
∴∠ADC+∠ACD=90°,∠DAE+∠CAE=90°,
∴∠CAE=∠ACD,
∴EA=EC,
∵∠AED=45°=∠CAE+∠ACD,
∴∠ACD=22.5°,
∵AB=AC,∠BAC=90°,
∴∠ACB=45°,
∴∠BCD=∠ACD=22.5°,
∴CD平分∠ACB.
②解:如图1中,过点D作DT⊥BC于T.
∵CD平分∠ACB,DT⊥CB,DA⊥CA,
∴DA=DT,
∵AB=AC,∠BAC=90°,
∴∠B=45°,
∴BD=DT=AD,
∴=.
(2)解:如图2中,连接BE,过点C作CT⊥AT交AE的延长线于T.
∵AE⊥BE,CT⊥AT,
∴∠AEB=∠T=∠BAC=90°,
∴∠BAE+∠ABE=90°,∠BAE+∠CAE=90°,
∴∠ABE=∠CAT,
∵AB=AC,
∴△ABE≌△CAT(AAS),
∴AE=CT,BE=AT,
∵∠AED=∠CET=45°,∠T=90°,
∴ET=CT=AE,
∴BE=2AE,
∴tan∠ABE==
一.选择题(共12小题)
1.如图,在△ABC中,∠ABC=90°,tan∠BAC=,AD=2,BD=4,连接CD,则CD长的最大值是( )
A.2+ B.2+1 C.2+ D.2+2
2.如图,在△ABC中,点O是角平分线AD、BE的交点,若AB=AC=10,BC=12,则tan∠OBD的值是( )
A. B.2 C. D.
3.如图,△ABC底边BC上的高为h1,△PQR底边QR上的高为h2,则有( )
A.h1=h2 B.h1<h2
C.h1>h2 D.以上都有可能
4.如图,已知在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足是D,设∠CAB=α,CD=h,那么BC的长度为( )
A. B. C. D.h?cosα
5.如图,△ABC的顶点是正方形网格的格点,则cos∠ABC的值为( )
A. B. C. D.
6.如图,在4×4的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值为( )
A.2 B. C. D.
7.在Rt△ABC中,∠C=90°,下列关系式中错误的是( )
A.BC=AB?sinA B.BC=AC?tanA C.AC=BC?tanB D.AC=AB?cosB
8.在Rt△ABC中,∠C=90°,cosB=,则Rt△ABC的三边a、b、c之比a:b:c为( )
A.2::3 B.1:: C.1:2:3 D.2::
9.在△ABC中,BC=2,AC=2,∠A=30°,则AB的长为( )
A. B.2 C.或4 D.2或4
10.如图,在△ABC中,AB=AC=4,∠C=72°,D是AB的中点,DE⊥AB交AC于点E,则cosA的值为( )
A. B. C. D.
11.在△ABC中,如果sinA=,cotB=,那么这个三角形一定是( )
A.等腰三角形 B.锐角三角形 C.钝角三角形 D.直角三角形
12.如图,已知∠ABC=60°,BD是∠ABC的平分线,BE是∠CBD的平分线,O,P分别是BD,BE上的动点(与点B不重合),分别过点O,P作OM⊥BC,PN⊥BC,垂足分别是点M,N.当点M,N重合时,的值是( )
A.+1 B.2﹣3 C.2 D.
二.填空题(共4小题)
13.将一副直角三角板拼成如图所示的四边形ABCD,一边重合,若∠CAB=45°,∠CAD=30°,连接BD,则tan∠DBC= .
14.如图△ABC中∠ACB=90°,D在AC上,AD=4CD,若∠BAC=2∠CBD,则tanA= .
15.在Rt△ABC中,∠C=90°,sinB=,若斜边上的高CD=2,则AC= .
16.在△ABC中,AB=2AC,tanB=,BC边上的高长为2,则△ABC的面积为 .
三.解答题(共4小题)
17.如图,在Rt△ABC中,∠A=90°,作BC的垂直平分线交AC于点D,延长AC至点E,使CE=AB.
(1)若AE=1,求△ABD的周长;
(2)若AD=BD,求tan∠ABC的值.
18.如图1,△ABC中,D为AC边上一动点(不含端点),过点D作DE∥AB交BC于点E,过点E作EF∥AC交AB于点F,连接AE,DF.点D运动过程中,始终有AE=DF.
(1)求证:∠BAC=90°;
(2)如图2,若AC=3,tanB=,当AF=AD时,求AD的长.
19.如图,在△ABC中,AD是BC边上的高,tanB=cos∠DAC.
(1)求证:AC=BD;
(2)若sinC=,BC=12,求△ABC的面积.
20.已知△ABC,AB=AC,∠BAC=90°,D是AB边上一点,连接CD,E是CD上一点,且∠AED=45°.
(1)如图1,若AE=DE,
①求证:CD平分∠ACB;
②求的值;
(2)如图2,连接BE,若AE⊥BE,求tan∠ABE的值.
参考答案
一.选择题(共12小题)
1.解:如图,在AD的下方作Rt△ADT,使得∠ADT=90°,DT=1,连接CT,则AT=,
∵==2,
∴=,
∵∠ADT=∠ABC=90°,
∴△ADT∽△ABC,
∴∠DAT=∠BAC,=
∴∠DAB=∠TAC,
∵=,
∴△DAB∽△TAC,
∴==,
∴TC=2,
∵CD≤DT+CT,
∴CD≤1+2,
∴CD的最大值为1+2,
故选:B.
2.解:如图:
作OF⊥AB于F,
∵AB=AC,AD平分∠BAC.
∴∠ODB=90°.BD=CD=6.
∴根据勾股定理得:AD==8.
∵BE平分∠ABC.
∴OF=OD,BF=BD=6,AF=10﹣6=4.
设OD=OF=x,则AO=8﹣x,在Rt△AOF中,根据勾股定理得:
(8﹣x)2=x2+42.
∴x=3.
∴OD=3.
在Rt△OBD中,tan∠OBD===.
故选:A.
3.解:如图,分别作出△ABC底边BC上的高为AD即h1,△PQR底边QR上的高为PE即h2,
在Rt△ADC中,h1=AD=5×sin55°,
在Rt△PER中,h2=PE=5×sin55°,
∴h1=h2,
故选:A.
4.解:∵CD⊥AB,
∴∠CAD+∠DCA=90°,
∵∠ACB=∠ACD+∠BCD=90°,
∴∠BCD=∠CAD=α,
在Rt△BCD中,
∵cos∠BCD=,CD=h,
∴BC=.
故选:B.
5.解:法一、如图,
在Rt△ABD中,∠ADB=90°,AD=BD=3,
∴AB===3,
∴cos∠ABC===.
故选:B.
法二、在Rt△ABD中,∠ADB=90°,AD=BD=3,
∴∠ABD=∠BAD=45°,
∴cos∠ABC=cos45°=.
故选:B.
6.解:∵AC2=12+22=5,
AB2=22+42=20,
BC2=32+42=25,
∴AC2+AB2=BC2.
∴∠CAB=90°.
∴tan∠ABC=.
故选:C.
7.解:如图所示:
∵sinA=,∴BC=sinA×AB,故选项A正确;
∵tanA=,∴BC=tanA×AC,故选项B正确;
∵tanB=,∴AC=tanB×BC,故选项C正确;
∵cosB=,∴BC=cosB×AB≠AC,故选项D错误.
故选:D.
8.解:∵∠C=90°,
∴cosB==,
设a=2x,c=3x,
∴b==x,
∴a:b:c=2x:x:3x=2::3.
故选:A.
9.解:作CD⊥AB交AB的延长线于点D,
当B2C=2时,
∵∠A=30°,∠ADC=90°,AC=2,
∴CD=,
∴AD==3,B2D==1,
∴AB2=3﹣1=2,
同理可得,AB1=3+1=4,
即AB的长为2或4,
故选:D.
10.解:∵在△ABC中,AB=AC=4,∠C=72°,
∴∠ABC=∠C=72°,∠A=180°﹣∠C﹣∠ABC=36°.
∵D是AB中点,DE⊥AB,
∴AE=BE,AD=BD=AB=2,
∴∠ABE=∠A=36°,
∴∠BEC=∠A+∠ABE=72°=∠C,
∴BE=BC=AE,
设BC=AE=x,则CE=AC﹣AE=4﹣x.
∵∠ABC=∠BEC,∠C=∠C,
∴△ABC∽△BEC,
∴=,
即=,
解得:x1=2﹣2,x2=﹣2﹣2(舍去),
∴AE=2﹣2,
∴cosA===,
故选:C.
11.解:∵sinA=,cotB=,
∴∠A=30°,∠B=60°,
∴∠C=180°﹣30°﹣60°=90°,
∴△ABC是直角三角形,
故选:D.
12.解:当M,N重合时,点P在OM上,如图,过点P作PH⊥BD于H,
∵BE是∠CBD的平分线,PN⊥BC,
∴PH=PM,
∵∠ABC=60°,BD是∠ABC的平分线,
∴∠CBD=∠ABC=30°,
∴∠BOP=90°﹣30°=60°,
∵在Rt△POH中,
PO==PH,
∴=+1.
故选:A.
二.填空题(共4小题)
13.解:作DE⊥BC,交BC延长线于点E,设CD=x,
∵∠CAB=45°,∠CAD=30°,一副直角三角板拼成的四边形ABCD,
∴∠ACB=90°,∠ADC=90°,
∴∠DCE=30°,
∴BC=AC=2x,DE=x,CE=x,
∴tan∠DBC===.
故答案为:.
14.解:延长AC至E,使CE=CD,连接BE,
∵∠ACB=90°,
∴BC⊥AC,
∵CE=CD,
∴BC是DE的垂直平分线,
∴BD=BE,
∴∠E=∠BDE,
设∠CBD=α,则∠BAC=2α,
∴∠E=∠BDE=90°﹣α,
∴∠ABE=180°﹣∠E﹣BAC=180°﹣(90°﹣α)﹣2α=90°﹣α,
∴∠E=∠ABE,
∴AB=AE,
设CD=x,则AD=4x,
∴AE=AB=6x,AC=5x,
在Rt△ABC中,BC===x,
∴tanA==.
故答案为:.
15.解:在Rt△ABC中,∠C=90°,
∴∠A+∠B=90°.
∵CD⊥AB,
∴∠A+∠ACD=90°.
∴∠ACD=∠B.
∵sinB=,
∴sin∠ACD=.
∵sin∠BCD=.
∴=.
设AD=a,则AC=3a.
.
∵CD=2,
∴2.
∴a=.
∴AC=.
故答案为:.
16.解:在Rt△ADB中,tanB=,
∴=,
解得,BD=6,
由勾股定理得,AB===2,
∴AC===,
由勾股定理得,CD===1,
如图1,BC=CD+BD=1+6=7,
∴△ABC的面积=×BC×AD=×7×2=7,
如图2,BC=BD﹣CD=6﹣1=5,
∴△ABC的面积=×BC×AD=×5×2=5,
∴△ABC的面积为7或5,
故答案为:7或5.
三.解答题(共4小题)
17.解:(1)如图,连接BD,设BC垂直平分线交BC于点F,
∴BD=CD,
C△ABD=AB+AD+BD
=AB+AD+DC
=AB+AC,
∵AB=CE,
∴C△ABD=AC+CE=AE=1,
故△ABD的周长为1.
(2)设AD=x,
∴BD=3x,
又∵BD=CD,
∴AC=AD+CD=4x,
在Rt△ABD中,AB===2.
∴tan∠ABC===.
18.(1)证明:∵DE∥AB,EF∥AC,
∴四边形ADEF是平行四边形.
∵AE=DF,
∴?ADEF是矩形.
∴∠BAC=90°.
(2)解:当AF=AD时,
由(1)知,此时四边形ADEF是正方形.
方法1,
∵DE∥AB,
∴∠DEC=∠B,∠EDC=∠BAC=90°.
∴tan∠DEC=tanB=.
在Rt△DEC中,设DC=3x,则DE=4x.
∵四边形ADEF是正方形,
∴AD=DE=4x.
∴AC=AD+DC=7x=3.
∴x=,
∴AD=4x=.
方法2:
在Rt△ABC中,∠BAC=90°,tanB=,AC=3,
∴AB=4.
∵四边形ADEF是正方形,设AD=DE=x.
∵DE∥AB,
∴△CED∽△CBA.
∴,
即,
解得x=,
∴AD=.
19.(1)证明:∵AD是BC边上的高,
∴∠ADB=∠ADC=90°,
∵tanB=cos∠DAC,
∴=,
∴BD=AC;
(2)解:设AC=BD=x,
∴CD=BC﹣BD=12﹣x,
∵sinC=,
∴cosC=,tanC=,
∴=,=,
即=,
解得:x=,
∴CD=12﹣x=,
∴AD=CD=×=8,
∴△ABC的面积=BC×AD=×12×8=48.
20.(1)①证明:∵AE=DE,
∴∠ADE=∠DAE,
∵∠CAD=90°,
∴∠ADC+∠ACD=90°,∠DAE+∠CAE=90°,
∴∠CAE=∠ACD,
∴EA=EC,
∵∠AED=45°=∠CAE+∠ACD,
∴∠ACD=22.5°,
∵AB=AC,∠BAC=90°,
∴∠ACB=45°,
∴∠BCD=∠ACD=22.5°,
∴CD平分∠ACB.
②解:如图1中,过点D作DT⊥BC于T.
∵CD平分∠ACB,DT⊥CB,DA⊥CA,
∴DA=DT,
∵AB=AC,∠BAC=90°,
∴∠B=45°,
∴BD=DT=AD,
∴=.
(2)解:如图2中,连接BE,过点C作CT⊥AT交AE的延长线于T.
∵AE⊥BE,CT⊥AT,
∴∠AEB=∠T=∠BAC=90°,
∴∠BAE+∠ABE=90°,∠BAE+∠CAE=90°,
∴∠ABE=∠CAT,
∵AB=AC,
∴△ABE≌△CAT(AAS),
∴AE=CT,BE=AT,
∵∠AED=∠CET=45°,∠T=90°,
∴ET=CT=AE,
∴BE=2AE,
∴tan∠ABE==
