第2章随机变量及其分布专题专解4 离散型随机变量的均值与方差 必备知识点+巩固练习-2020-2021学年人教A版高中数学选修2-3(含答案)
文档属性
| 名称 | 第2章随机变量及其分布专题专解4 离散型随机变量的均值与方差 必备知识点+巩固练习-2020-2021学年人教A版高中数学选修2-3(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 411.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-30 00:00:00 | ||
图片预览




文档简介
-86360-36195专题四 离散型随机变量的均值与方差
专题四 离散型随机变量的均值与方差
【必备知识点】
一.离散型随机变量的期望
1.定义:
一般地,若离散型随机变量的概率分布为
…
…
P
…
…
则称…… 为的均值或数学期望,简称期望.
2.性质:
①;
②若(a、b是常数),是随机变量,则也是随机变量,有;
的推导过程如下::
的分布列为
…
…
…
…
P
…
…
于是……
=……)……)=
∴。
二.离散型随机变量的方差与标准差
1.一组数据的方差的概念:
已知一组数据,,…,,它们的平均值为,那么各数据与的差的平方的平均数
++…+叫做这组数据的方差。
2.离散型随机变量的方差:
一般地,若离散型随机变量的概率分布为
…
…
P
…
…
则称=++…++…称为随机变量的方差,式中的是随机变量的期望.
的算术平方根叫做随机变量的标准差,记作.
3.期望和方差的关系:
4.方差的性质:
若(a、b是常数),是随机变量,则也是随机变量,;
三.常见分布的期望与方差
1、二点分布:
若离散型随机变量服从参数为的二点分布,则
期望
方差
证明:∵,,,
∴
2、二项分布:
若离散型随机变量服从参数为的二项分布,即则
期望
方差
期望公式证明:
∵,
∴,
又∵,
∴++…++…+
.
3、几何分布:
独立重复试验中,若事件在每一次试验中发生的概率都为,事件第一次发生时所做的试验次数是随机变量,且,,称离散型随机变量服从几何分布,记作:。
若离散型随机变量服从几何分布,且则
期望
方差
要点诠释:随机变量是否服从二项分布或者几何分布,要从取值和相应概率两个角度去验证。
4、超几何分布:
若离散型随机变量服从参数为的超几何分布,则
期望
四.离散型随机变量的期望与方差的求法及应用
1、求离散型随机变量的期望、方差、标准差的基本步骤:
①理解的意义,写出可能取的全部值;
②求取各个值的概率,写出分布列;
…
…
P
…
…
③根据分布列,由期望、方差的定义求出、、:
.
2.离散型随机变量的期望与方差的实际意义及应用
① 离散型随机变量的期望,反映了随机变量取值的平均水平;
② 随机变量的方差与标准差都反映了随机变量取值的稳定与波动、集中与离散的程度。方差越大数据波动越大。
③对于两个随机变量和,当需要了解他们的平均水平时,可比较和的大小。
④和相等或很接近,当需要进一步了解他们的稳定性或者集中程度时,比较和,方差值大时,则表明ξ比较离散,反之,则表明ξ比较集中.品种的优劣、仪器的好坏、预报的准确与否、武器的性能等很多指标都与这两个特征数(数学期望、方差)有关.
【典例展示】
例1. 已知随机变量X的分布列为:
X
-2
-1
0
1
2
P
false
false
false
m
false
试求:(1)E(X);(2)若y=2X-3,求E(Y).
【解析】
(1)由随机变量分布列的性质,得
false,false,
∴false。
(2)解法一:由公式E(aX+b)=aE(X)+b,得
false.
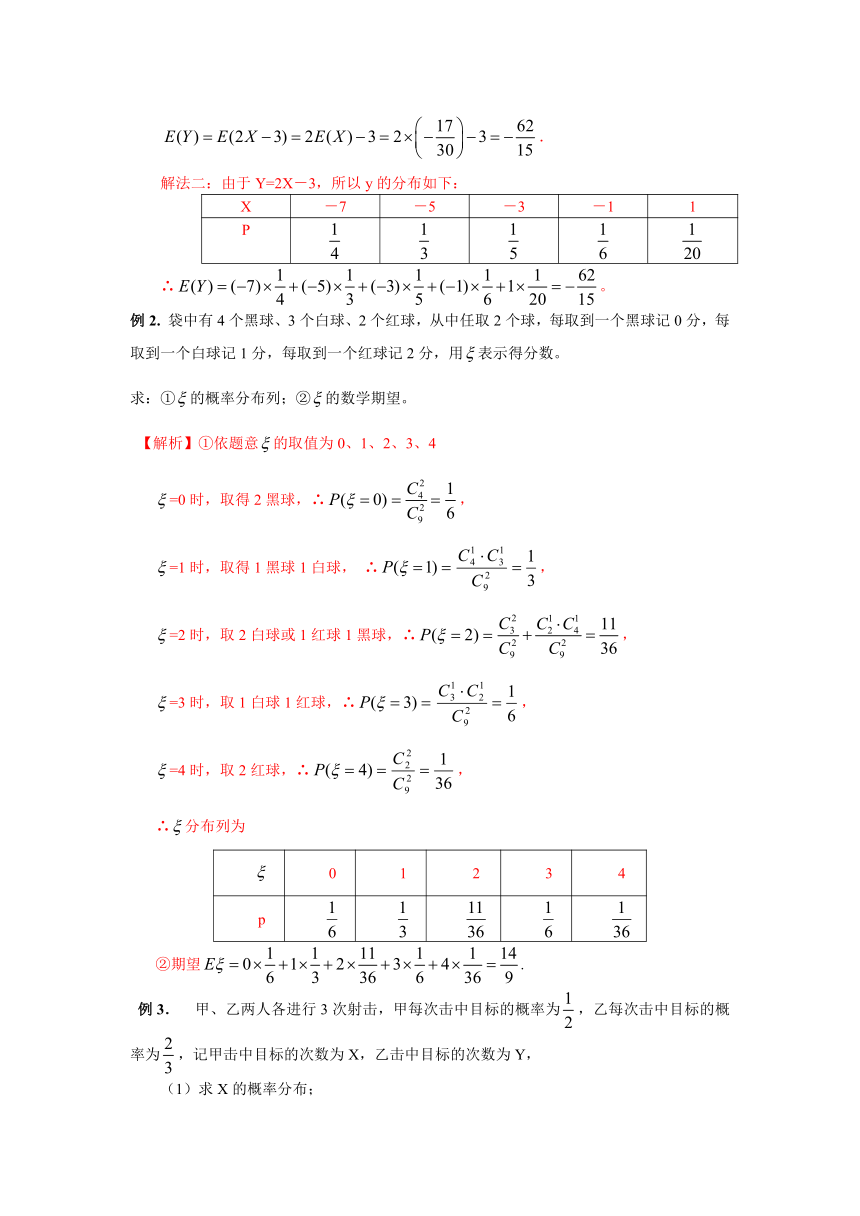
解法二:由于Y=2X-3,所以y的分布如下:
X
-7
-5
-3
-1
1
P
false
false
false
false
false
∴false。
例2. 袋中有4个黑球、3个白球、2个红球,从中任取2个球,每取到一个黑球记0分,每取到一个白球记1分,每取到一个红球记2分,用false表示得分数。
求:①false的概率分布列;②false的数学期望。
【解析】①依题意false的取值为0、1、2、3、4
false=0时,取得2黑球,∴false,
false=1时,取得1黑球1白球, ∴falsefalse,
false=2时,取2白球或1红球1黑球,∴falsefalse,
false=3时,取1白球1红球,∴falsefalse,
false=4时,取2红球,∴falsefalse,
∴false分布列为
false
0
1
2
3
4
p
false
false
false
false
false
②期望false.
例3. 甲、乙两人各进行3次射击,甲每次击中目标的概率为false,乙每次击中目标的概率为false,记甲击中目标的次数为X,乙击中目标的次数为Y,
(1)求X的概率分布;
(2)求X和Y的数学期望.
【解析】(1)false,
false,
false,
false。
所以X的概率分布如下表:
X
0
1
2
3
P
false
false
false
false
(2)由(1)知false,
或由题意false,false。
∴false,false。
例4.已知离散型随机变量false的概率分布为
false
1
2
3
4
5
6
7
P
false
false
false
false
false
false
false
离散型随机变量false的概率分布为
false
3.7
3.8
3.9
4
4.1
4.2
4.3
P
false
false
false
false
false
false
false
求这两个随机变量期望、均方差与标准差
【解析】false;
false;false
false;
false=0.04, false.
例5.有一批数量很大的商品的次品率为1%,从中任意地连续取出20件商品,求抽出次品数的期望与方差。
【解析】设抽出次品数为false,因为被抽商品数量相当大,抽20件商品可以看作20次独立重复试验,
所以false,
所以false
false
例6. 甲、乙两种水稻在相同条件下各种植100亩,收获的情况如下:
甲:
亩产量
300
320
330
340
亩数
20
25
40
15
乙:
亩产量
310
320
330
340
亩数
30
20
40
10
试评价哪种水稻的质量较好.
【解析】 设甲、乙两种水稻的亩产量分别为X和Y.
则false,false,
false,false。
且false,false,
false,false。
∴false,
false,
即E(X)=E(Y),这表明两种水稻的平均亩产量相同,进一步求各自的方差,得
false,
false。
即V(X)>V(Y),这说明乙种水稻的产量较为稳定,因此乙种水稻质量较好.
【巩固练习】
1.已知某射手射击所得环数false的分布列如下:
false
4
5
6
7
8
9
10
P
0.02
0.04
0.06
0.09
0.28
0.29
0.22
求false.
【答案】
false false
false。
2.已知随机变量ξ的分布列为
ξ
-2
-1
0
1
2
3
P
false
m
n
false
false
false
其中m,n∈[0,1),且E(ξ)=false,则m,n的值分别为________.
【答案】false,false
由p1+p2+…+p6=1,得m+n=false,
由E(ξ)=false,得false-m=false,
∴m=false,n=false.
3.随机变量ξ的分布列为:
ξ
0
2
4
P
0.4
0.3
0.3
则E(5ξ+4)等于( )
A.13 B.11 C.2.2 D.2.3
【答案】A
由已知得
E(ξ)=0×0.4+2×0.3+4×0.3=1.8,
∴E(5ξ+4)=5E(ξ)+4=5×1.8+4=13.
4.设离散型随机变量false的可能取值为1,2,3,4,且false(false),false,则false ;
【答案】false;
由分布列的概率和为1,有false,
又false,即false,
解得false,false,故false。
5. 随机的抛掷一个骰子,求所得骰子的点数ξ的数学期望.
【答案】抛掷骰子所得点数ξ的概率分布为
ξ
1
2
3
4
5
6
P
false
false
false
false
false
false
所以
false1×false+2×false+3×false+4×false+5×false+6×false=(1+2+3+4+5+6)×false=3.5.
抛掷骰子所得点数ξ的数学期望,就是ξ的所有可能取值的平均值.
6.甲、乙、丙、丁独立地破译一个密码,其中甲的成功率是false,乙、丙、丁的成功率都是false.
(1)若破译密码成功的人数为X,求X的概率分布;
(2)求破译密码成功人数的数学期望.
【答案】
(1)破译密码成功的人数X的可能取值为0,1,2,3,4.
false,
false,
false,
false,
false,
则X的概率分布表为
X
0
1
2
3
4
P
false
false
false
false
false
(2)由(1)知false,
即破译密码成功的人数的数学期望为1.5.
7.交5元钱,可以参加一次抽奖,已知一袋中有同样大小的球10个,其中有8个标有1元钱,2个标有5元钱,抽奖者只能从中任取2个球,他所得奖励是所抽2球的钱数之和.求抽奖者获利的数学期望.
【答案】 抽到的2个球上的钱数之和ξ是个随机变量,其中ξ取每一个值时所代表的随机事件的概率是容易获得的,本题的目标是求参加抽奖的人获利false的数学期望,由ξ与false的关系为false=ξ-5,利用公式
E(false)=E(ξ)-5可获解答.
设ξ为抽到的2球钱数之和,则ξ的取值如下:
ξ=2(抽到2个1元),ξ=6(抽到1个1元,1个5元),ξ=10(抽到2个5元).
所以,由题意得false,false,false,
∴false.
又设false为抽奖者获利的可能值,则false=ξ-5,所以抽奖者获利的期望为
false.
8. 有一批数量很大的商品的次品率为1%,从中任意地连续取出20件商品,求抽出次品数的期望。
【答案】设抽出次品数为false,因为被抽商品数量相当大,抽20件商品可以看作20次独立重复试验,
所以false,
所以false
9.一次单元测验由20个选择题构成,每个选择题有4个选项,其中有且仅有一个选项是正确答案,每题选择正确答案得5分,不作出选择或选错不得分,满分100分 学生甲选对任一题的概率为0.9,学生乙则在测验中对每题都从4个选择中随机地选择一个,求学生甲和乙在这次英语单元测验中的成绩的期望。
【答案】设学生甲和乙在这次英语测验中正确答案的选择题个数分别是false,
则false~ B(20,0.9),false,
false
由于答对每题得5分,学生甲和乙在这次英语测验中的成绩分别是5false和5false 所以,他们在测验中的成绩的期望分别是:
false
10.已知随机变量ξ的分布列如下表:
ξ
-1
0
1
P
false
false
false
(1)求E(ξ),D(ξ),η;
(2)设η=2ξ+3,求E(η),D(η).
【答案】(1)false;
false,false。
(2)false,false。
11.设随机变量X的概率分布为
X
1
2
…
n
P
false
false
…
false
求D(X)。
【答案】 本题考查方差的求法.可由分布列先求出X的期望E(X),再利用方差的定义求之.也可直接利用公式D(X)=E(X2)-[E(X)]2来解.
解法一:
false
false,
∴false
falsefalse。
解法二:由解法一可求得false。
又false
falsefalse,
∴false。
12.若某批产品共100件,其中有20件二等品,从中有放回地抽取3件,求取出二等品的件数的期望、方差。
【答案】由题知一次取出二等品的概率为false,有放回地抽取3件,可以看作3次独立重复试验,
即取出二等品的件数false,
所以false,
false.
13.甲、乙两个野生动物保护区有相同的自然环境,且野生动物的种类和数量也大致相等.而两个保护区内每个季度发现违反保护条例的事件次数的概率分布分别为
甲保护区:
X1
0
1
2
3
P
0.3
0.3
0.2
0.2
乙保护区:
X2
0
1
2
P
0.1
0.5
0.4
试评定这两个保护区的管理水平.
【答案】甲保护区的违规次数X1的数学期望和方差分别为:
E(X1)=0×0.3+1×0.3+2×0.2+3×0.2=1.3;
D(X1)=(0-1.3)2×0.3+(1-1.3)2×0.3+(2-1.3)2×0.2+(3-1.3)2×0.2=1.21.
乙保护区的违规次数置的数学期望和方差分别为:
E(X2)=0×0.1+1×0.5+2×0.4=1.3;
D(X2)=(0-1.3)2×0.1+(1-1.3)2×0.5+(2-1.3)2×0.4=0.41.
因为E(X1)=E(X2),D(X1)>D(X2),所以两个保护区内每季度平均发生的违规事件次数是相同的,但乙保护区内发生的违规事件次数更集中和稳定,而甲保护区内发生的违规事件次数相对分散,波动较大.
14. 根据气象预报,某地区近期有小洪水的概率为0.25,有大洪水的概率为0.01,该地区某工地上有一台大型设备,遇到大洪水时要损失60000元,遇到小洪水时要损失10000元.为保护设备,有以下3种方案:
方案1:运走设备,搬运费为3800元:
方案2:建保护围墙,建设费为2000元,但围墙只能防小洪水;
方案3:不采取措施,希望不发生洪水.
试比较哪一种方案好.
【答案】 要比较哪一种方案好,只要把三种方案的损失的数学期望求出,哪一个小,哪一个方案就好.
用X1、X2、X3分别表示三种方案的损失.
采用方案1:无论有无洪水,都损失3800元,即X=3800.
采用方案2:遇到大洪水时,损失2000+60000=62000(元);没有大洪水时,损失2000元,即
false.
同样,采用方案3:有false.
于是,E(X1)=3800,
E(X2)=62000×P (X2=62000)+2000×P (X2=2000)=62000×0.01+2000×(1-0.01)=2600,
E(X3)=60000×P (X3=60000)+10000×P(X3=10000)+0×P (X3=0)=60000×0.01+10000×0.25=3100.
采用方案2的平均损失最小,所以方案2好.
【课后练习】
一、选择题
1.设随机变量X的分布列如下表所示且E(X)=1.6,则a-b=( )
X
0
1
2
3
P
0.1
a
b
0.1
A.0.2 B.0.1 C.-0.2 D.-0.4
2.已知ξ的分布列为
ξ
0
1
P
p
q
其中P∈(0,1),则( )
(A) Eξ=p,Dξ=pq (B) Eξ=p,Dξ=p2
(C) Eξ=q,Dξ=q2 (D) Eξ=l一p,Dξ=p-p2
3.已知随机变量X的分布列为:P(X=k)=,k=1、2、3,则D(3X+5)=( )
A.6 B.9 C.3 D.4
4.一台机器生产某种产品,如果生产一件甲等品可获利50元,生产一件乙等品可获利30元,生产一件次品,要赔20元,已知这台机器生产甲等品、乙等品和次品的概率分别为0.6、0.3和0.1,则这台机器每生产一件产品,平均预期可获得( )
A.36元 B.37元
C.38元 D.39元
5.一牧场有10头牛,因误食含有病毒的饲料而被感染,已知该病的发病率为0.02.设发病的牛的头数为ξ,则Dξ等于( )
A.0.2 B.0.8 C.0.196 D.0.804
6.甲、乙两台自动车床生产同种标准件,X表示甲机床生产1 000件产品中的次品数,Y表示乙机床生产1 000件产品中的次品数,经过一段时间的考查,X、Y的分布列分别为
X
0
1
2
3
P
0.7
0.1
0.1
0.1
Y
0
1
2
3
P
0.5
0.3
0.2
0
据此判断( )
A.甲比乙质量好 B.乙比甲质量好
C.甲与乙质量相同 D.无法判定
7.某种种子每粒发芽的概率都为0.9,现播种了1 000粒,对于没有发芽的种子,每粒需再补种2粒,补种的种子数记为X,则X的均值为( )
A.100 B.200 C.300 D.400
8.甲、乙、丙三名射箭运动员在某次测试中各射箭20次,三人的测试成绩如下表:
41211570485甲的成绩
环数
7
8
9
10
频数
5
5
5
5
乙的成绩
环数
7
8
9
10
频数
6
4
4
6
丙的成绩
环数
7
8
9
10
频数
4
6
6
4
甲的成绩
环数
7
8
9
10
频数
5
5
5
5
乙的成绩
环数
7
8
9
10
频数
6
4
4
6
丙的成绩
环数
7
8
9
10
频数
4
6
6
4
s1,s2,s3分别表示甲、乙、丙三名运动员这次测试成绩的标准差,则有( ).
A.s3>s1>s2 B.s2>s1>s3 C.s1>s2>s3 D.s2>s3>s1
二、填空题
9.有两台自动包装机甲与乙,包装重量分别为随机变量ξ1、ξ2,若Eξ1=Eξ2,Dξ1>Dξ2,则自动包装机________的质量较好.
10.随机变量ξ的分布列如下:
ξ
-1
0
1
P
a
b
c
其中a,b,c成等差数列.若,则D(ξ)的值是________.
11.节日期间,某种鲜花进货价是每束2.5元,销售价是每束5元;节后卖不出的鲜花以每束1.6元处理,根据前五年销售情况预测,节日期间这种鲜花的需求量X服从如表所示的概率分布:
X
200
300
400
500
P
0.20
0.35
0.30
0.15
若进这种鲜花500束,则期望利润是________元.
12.某射手有5发子弹,射击一次,命中率是0.9,如果命中了就停止射击,否则一直射到子弹用尽为止,设损耗子弹数为X,则E(X)=________,D(X)=________.(精确到0.01)
三、解答题
13. 已知盒中有10个灯泡,其中8个正品,2个次品需要从中取出2个正品,每次取出1个,取出后不放回,直到取出2个正品为止设ξ为取出的次数,求ξ的分布列及Eξ
14.设在12个同类型的零件中有2个次品,抽取3次进行检验,每次抽取一个,并且取出后不再放回,若以X和V分别表示取出次品和正品的个数.
(1)求X的概率分布、期望值及方差;
(2)求Y的概率分布、期望值及方差.
15.有甲、乙两个建材厂,都想投标参加某重点建设,为了对重点建设负责,政府到两建材厂抽样检查,他们从中各取等量的样品:检查它们的抗拉强度指数如下:
ξ
110
120
125
130
135
P
0.1
0.2
0.4
0.1
0.2
η
100
115
125
130
145
P
0.1
0.2
0.4
0.1
0.2
其中ξ和η分别表示甲、乙两厂材料的抗拉强度,在要求抗拉强度不低于120的条件下,比较甲、乙两厂材料哪一种稳定性较好.
【答案与解析】
1.【答案】 C
【解析】 由0.1+a+b+0.1=1,得a+b=0.8,①
又由E(X)=0×0.1+1×a+2×b+3×0.1=1.6,
得a+2b=1.3,②
由①②解得a=0.3,b=0.5,∴a-b=-0.2,故应选C.
2. 【答案】D
【解析】ξ~B(l,q),p+q=1.
3. 【答案】 A
【解析】 E(X)=(1+2+3)×=2,
D(X)=[(1-2)2+(2-2)2+(3-2)2]×=23,
∴D(3X+5)=9D(X)=6.
4. 【答案】B
【解析】由题意知每生产一件产品,平均预期可获利0.6×50+0.3×30+0.1×(-20)=37(元).
5. 【答案】C
【解析】根据二项分布的方差公式:Dξ=10×0.02×0.98=0.196.
6. 【答案】A
【解析】EX=0.7×0+1×0.1+2×0.1+3×0.1=0.6,
EY=0×0.5+1×0.3+2×0.2+3×0=0.7,
因为EX7. 【答案】 B
【解析】 本题以实际问题为背景,考查的事件的均值问题.
记“不发芽的种子数为ξ”,则ξ~B(1 000,0.1),所以E(ξ)=1 000×0.1=100,而X=2ξ,故EX=E(2ξ)=2E(ξ)=200,故选B.
8.【答案】B
【解析】 设甲、乙、丙射中的环数依次为X1、X2、X3。依题意对甲有:
X1
7
8
9
10
P
,
,;
对乙有:
X2
7
8
9
10
P
,
,;同理可得。故s2>s1>s3。
9. 【答案】乙
【解析】Eξ1=Eξ2说明甲、乙两机包装的重量的平均水平一样.Dξ1>Dξ2说明甲机包装重量的差别大,不稳定.∴乙机质量好.
10.【答案】
【解析】 依随机变量的分布列知a+b+c=1,
依a,b,c成等差数列知2b=a+c,则,。
又,则。
解得,,。
故。
11.【答案】706
【解析】 节日期间鲜花预售量为
E(X)=200×0.20+300×0.35+400×0.30+500×0.15=40+105+120+75=340,
则期望的利润Y=5X+1.6(500―X)―500×2.5=3.4X―450,
∴E(Y)=3.4 E(X)―450=3.4×340―450=706。
故期望利润为706元。
12.【答案】1.11 0.12
【解析】随机变量X服从超几何分布,根据公式:期望方差可求。
13. 【解析】
每次取1件产品,∴至少需2次,即ξ最小为2,有2件次品,当前2次取得的都是次品时,ξ=4,所以ξ可以取2,3,4
P(ξ=2)=×=;
P(ξ=3)=××+××=;P(ξ=4)=1--=
∴ξ的分布列如下:
ξ
2
3
4
P
Eξ=2×P(ξ=2)+3×P(ξ=3)+4×P(ξ=4)=
14.【解析】(1)X的可能取值为0,1,2。
若X=0,表示没有取出次品,其概率为,
同理,有,。
∴X的概率分布为
X
0
1
2
P
∴,
D(。
(2)Y的可能取值为1,2,3,显然X+Y=3。
,,
。
∴Y的概率分布为
Y
1
2
3
P
∴。
∵Y=-X+3,∴。
15.【解析】
E(ξ)=110×0.1+120×0.2+125×0.4+130×0.1+135×0.2=125,
E(η)=100×0.1+115×0.2+125×0.4+130×0.1+145×0.2=125,
D(ξ)=0.1×(110-125)2+0.2×(120-125)2+0.4×(125-125)2+0.1×(130-125)2+0.2-(135-125)2=50,
D(η)=0.1×(100-125)2+0.2×(115-125)2+0.4×(125-125)2+0.1×(130-125)2+0.2×(145-125)2=165,
由于E(ξ)=E(η),而D(ξ)<D(η),
故甲厂的材料稳定性较好。
专题四 离散型随机变量的均值与方差
【必备知识点】
一.离散型随机变量的期望
1.定义:
一般地,若离散型随机变量的概率分布为
…
…
P
…
…
则称…… 为的均值或数学期望,简称期望.
2.性质:
①;
②若(a、b是常数),是随机变量,则也是随机变量,有;
的推导过程如下::
的分布列为
…
…
…
…
P
…
…
于是……
=……)……)=
∴。
二.离散型随机变量的方差与标准差
1.一组数据的方差的概念:
已知一组数据,,…,,它们的平均值为,那么各数据与的差的平方的平均数
++…+叫做这组数据的方差。
2.离散型随机变量的方差:
一般地,若离散型随机变量的概率分布为
…
…
P
…
…
则称=++…++…称为随机变量的方差,式中的是随机变量的期望.
的算术平方根叫做随机变量的标准差,记作.
3.期望和方差的关系:
4.方差的性质:
若(a、b是常数),是随机变量,则也是随机变量,;
三.常见分布的期望与方差
1、二点分布:
若离散型随机变量服从参数为的二点分布,则
期望
方差
证明:∵,,,
∴
2、二项分布:
若离散型随机变量服从参数为的二项分布,即则
期望
方差
期望公式证明:
∵,
∴,
又∵,
∴++…++…+
.
3、几何分布:
独立重复试验中,若事件在每一次试验中发生的概率都为,事件第一次发生时所做的试验次数是随机变量,且,,称离散型随机变量服从几何分布,记作:。
若离散型随机变量服从几何分布,且则
期望
方差
要点诠释:随机变量是否服从二项分布或者几何分布,要从取值和相应概率两个角度去验证。
4、超几何分布:
若离散型随机变量服从参数为的超几何分布,则
期望
四.离散型随机变量的期望与方差的求法及应用
1、求离散型随机变量的期望、方差、标准差的基本步骤:
①理解的意义,写出可能取的全部值;
②求取各个值的概率,写出分布列;
…
…
P
…
…
③根据分布列,由期望、方差的定义求出、、:
.
2.离散型随机变量的期望与方差的实际意义及应用
① 离散型随机变量的期望,反映了随机变量取值的平均水平;
② 随机变量的方差与标准差都反映了随机变量取值的稳定与波动、集中与离散的程度。方差越大数据波动越大。
③对于两个随机变量和,当需要了解他们的平均水平时,可比较和的大小。
④和相等或很接近,当需要进一步了解他们的稳定性或者集中程度时,比较和,方差值大时,则表明ξ比较离散,反之,则表明ξ比较集中.品种的优劣、仪器的好坏、预报的准确与否、武器的性能等很多指标都与这两个特征数(数学期望、方差)有关.
【典例展示】
例1. 已知随机变量X的分布列为:
X
-2
-1
0
1
2
P
false
false
false
m
false
试求:(1)E(X);(2)若y=2X-3,求E(Y).
【解析】
(1)由随机变量分布列的性质,得
false,false,
∴false。
(2)解法一:由公式E(aX+b)=aE(X)+b,得
false.
解法二:由于Y=2X-3,所以y的分布如下:
X
-7
-5
-3
-1
1
P
false
false
false
false
false
∴false。
例2. 袋中有4个黑球、3个白球、2个红球,从中任取2个球,每取到一个黑球记0分,每取到一个白球记1分,每取到一个红球记2分,用false表示得分数。
求:①false的概率分布列;②false的数学期望。
【解析】①依题意false的取值为0、1、2、3、4
false=0时,取得2黑球,∴false,
false=1时,取得1黑球1白球, ∴falsefalse,
false=2时,取2白球或1红球1黑球,∴falsefalse,
false=3时,取1白球1红球,∴falsefalse,
false=4时,取2红球,∴falsefalse,
∴false分布列为
false
0
1
2
3
4
p
false
false
false
false
false
②期望false.
例3. 甲、乙两人各进行3次射击,甲每次击中目标的概率为false,乙每次击中目标的概率为false,记甲击中目标的次数为X,乙击中目标的次数为Y,
(1)求X的概率分布;
(2)求X和Y的数学期望.
【解析】(1)false,
false,
false,
false。
所以X的概率分布如下表:
X
0
1
2
3
P
false
false
false
false
(2)由(1)知false,
或由题意false,false。
∴false,false。
例4.已知离散型随机变量false的概率分布为
false
1
2
3
4
5
6
7
P
false
false
false
false
false
false
false
离散型随机变量false的概率分布为
false
3.7
3.8
3.9
4
4.1
4.2
4.3
P
false
false
false
false
false
false
false
求这两个随机变量期望、均方差与标准差
【解析】false;
false;false
false;
false=0.04, false.
例5.有一批数量很大的商品的次品率为1%,从中任意地连续取出20件商品,求抽出次品数的期望与方差。
【解析】设抽出次品数为false,因为被抽商品数量相当大,抽20件商品可以看作20次独立重复试验,
所以false,
所以false
false
例6. 甲、乙两种水稻在相同条件下各种植100亩,收获的情况如下:
甲:
亩产量
300
320
330
340
亩数
20
25
40
15
乙:
亩产量
310
320
330
340
亩数
30
20
40
10
试评价哪种水稻的质量较好.
【解析】 设甲、乙两种水稻的亩产量分别为X和Y.
则false,false,
false,false。
且false,false,
false,false。
∴false,
false,
即E(X)=E(Y),这表明两种水稻的平均亩产量相同,进一步求各自的方差,得
false,
false。
即V(X)>V(Y),这说明乙种水稻的产量较为稳定,因此乙种水稻质量较好.
【巩固练习】
1.已知某射手射击所得环数false的分布列如下:
false
4
5
6
7
8
9
10
P
0.02
0.04
0.06
0.09
0.28
0.29
0.22
求false.
【答案】
false false
false。
2.已知随机变量ξ的分布列为
ξ
-2
-1
0
1
2
3
P
false
m
n
false
false
false
其中m,n∈[0,1),且E(ξ)=false,则m,n的值分别为________.
【答案】false,false
由p1+p2+…+p6=1,得m+n=false,
由E(ξ)=false,得false-m=false,
∴m=false,n=false.
3.随机变量ξ的分布列为:
ξ
0
2
4
P
0.4
0.3
0.3
则E(5ξ+4)等于( )
A.13 B.11 C.2.2 D.2.3
【答案】A
由已知得
E(ξ)=0×0.4+2×0.3+4×0.3=1.8,
∴E(5ξ+4)=5E(ξ)+4=5×1.8+4=13.
4.设离散型随机变量false的可能取值为1,2,3,4,且false(false),false,则false ;
【答案】false;
由分布列的概率和为1,有false,
又false,即false,
解得false,false,故false。
5. 随机的抛掷一个骰子,求所得骰子的点数ξ的数学期望.
【答案】抛掷骰子所得点数ξ的概率分布为
ξ
1
2
3
4
5
6
P
false
false
false
false
false
false
所以
false1×false+2×false+3×false+4×false+5×false+6×false=(1+2+3+4+5+6)×false=3.5.
抛掷骰子所得点数ξ的数学期望,就是ξ的所有可能取值的平均值.
6.甲、乙、丙、丁独立地破译一个密码,其中甲的成功率是false,乙、丙、丁的成功率都是false.
(1)若破译密码成功的人数为X,求X的概率分布;
(2)求破译密码成功人数的数学期望.
【答案】
(1)破译密码成功的人数X的可能取值为0,1,2,3,4.
false,
false,
false,
false,
false,
则X的概率分布表为
X
0
1
2
3
4
P
false
false
false
false
false
(2)由(1)知false,
即破译密码成功的人数的数学期望为1.5.
7.交5元钱,可以参加一次抽奖,已知一袋中有同样大小的球10个,其中有8个标有1元钱,2个标有5元钱,抽奖者只能从中任取2个球,他所得奖励是所抽2球的钱数之和.求抽奖者获利的数学期望.
【答案】 抽到的2个球上的钱数之和ξ是个随机变量,其中ξ取每一个值时所代表的随机事件的概率是容易获得的,本题的目标是求参加抽奖的人获利false的数学期望,由ξ与false的关系为false=ξ-5,利用公式
E(false)=E(ξ)-5可获解答.
设ξ为抽到的2球钱数之和,则ξ的取值如下:
ξ=2(抽到2个1元),ξ=6(抽到1个1元,1个5元),ξ=10(抽到2个5元).
所以,由题意得false,false,false,
∴false.
又设false为抽奖者获利的可能值,则false=ξ-5,所以抽奖者获利的期望为
false.
8. 有一批数量很大的商品的次品率为1%,从中任意地连续取出20件商品,求抽出次品数的期望。
【答案】设抽出次品数为false,因为被抽商品数量相当大,抽20件商品可以看作20次独立重复试验,
所以false,
所以false
9.一次单元测验由20个选择题构成,每个选择题有4个选项,其中有且仅有一个选项是正确答案,每题选择正确答案得5分,不作出选择或选错不得分,满分100分 学生甲选对任一题的概率为0.9,学生乙则在测验中对每题都从4个选择中随机地选择一个,求学生甲和乙在这次英语单元测验中的成绩的期望。
【答案】设学生甲和乙在这次英语测验中正确答案的选择题个数分别是false,
则false~ B(20,0.9),false,
false
由于答对每题得5分,学生甲和乙在这次英语测验中的成绩分别是5false和5false 所以,他们在测验中的成绩的期望分别是:
false
10.已知随机变量ξ的分布列如下表:
ξ
-1
0
1
P
false
false
false
(1)求E(ξ),D(ξ),η;
(2)设η=2ξ+3,求E(η),D(η).
【答案】(1)false;
false,false。
(2)false,false。
11.设随机变量X的概率分布为
X
1
2
…
n
P
false
false
…
false
求D(X)。
【答案】 本题考查方差的求法.可由分布列先求出X的期望E(X),再利用方差的定义求之.也可直接利用公式D(X)=E(X2)-[E(X)]2来解.
解法一:
false
false,
∴false
falsefalse。
解法二:由解法一可求得false。
又false
falsefalse,
∴false。
12.若某批产品共100件,其中有20件二等品,从中有放回地抽取3件,求取出二等品的件数的期望、方差。
【答案】由题知一次取出二等品的概率为false,有放回地抽取3件,可以看作3次独立重复试验,
即取出二等品的件数false,
所以false,
false.
13.甲、乙两个野生动物保护区有相同的自然环境,且野生动物的种类和数量也大致相等.而两个保护区内每个季度发现违反保护条例的事件次数的概率分布分别为
甲保护区:
X1
0
1
2
3
P
0.3
0.3
0.2
0.2
乙保护区:
X2
0
1
2
P
0.1
0.5
0.4
试评定这两个保护区的管理水平.
【答案】甲保护区的违规次数X1的数学期望和方差分别为:
E(X1)=0×0.3+1×0.3+2×0.2+3×0.2=1.3;
D(X1)=(0-1.3)2×0.3+(1-1.3)2×0.3+(2-1.3)2×0.2+(3-1.3)2×0.2=1.21.
乙保护区的违规次数置的数学期望和方差分别为:
E(X2)=0×0.1+1×0.5+2×0.4=1.3;
D(X2)=(0-1.3)2×0.1+(1-1.3)2×0.5+(2-1.3)2×0.4=0.41.
因为E(X1)=E(X2),D(X1)>D(X2),所以两个保护区内每季度平均发生的违规事件次数是相同的,但乙保护区内发生的违规事件次数更集中和稳定,而甲保护区内发生的违规事件次数相对分散,波动较大.
14. 根据气象预报,某地区近期有小洪水的概率为0.25,有大洪水的概率为0.01,该地区某工地上有一台大型设备,遇到大洪水时要损失60000元,遇到小洪水时要损失10000元.为保护设备,有以下3种方案:
方案1:运走设备,搬运费为3800元:
方案2:建保护围墙,建设费为2000元,但围墙只能防小洪水;
方案3:不采取措施,希望不发生洪水.
试比较哪一种方案好.
【答案】 要比较哪一种方案好,只要把三种方案的损失的数学期望求出,哪一个小,哪一个方案就好.
用X1、X2、X3分别表示三种方案的损失.
采用方案1:无论有无洪水,都损失3800元,即X=3800.
采用方案2:遇到大洪水时,损失2000+60000=62000(元);没有大洪水时,损失2000元,即
false.
同样,采用方案3:有false.
于是,E(X1)=3800,
E(X2)=62000×P (X2=62000)+2000×P (X2=2000)=62000×0.01+2000×(1-0.01)=2600,
E(X3)=60000×P (X3=60000)+10000×P(X3=10000)+0×P (X3=0)=60000×0.01+10000×0.25=3100.
采用方案2的平均损失最小,所以方案2好.
【课后练习】
一、选择题
1.设随机变量X的分布列如下表所示且E(X)=1.6,则a-b=( )
X
0
1
2
3
P
0.1
a
b
0.1
A.0.2 B.0.1 C.-0.2 D.-0.4
2.已知ξ的分布列为
ξ
0
1
P
p
q
其中P∈(0,1),则( )
(A) Eξ=p,Dξ=pq (B) Eξ=p,Dξ=p2
(C) Eξ=q,Dξ=q2 (D) Eξ=l一p,Dξ=p-p2
3.已知随机变量X的分布列为:P(X=k)=,k=1、2、3,则D(3X+5)=( )
A.6 B.9 C.3 D.4
4.一台机器生产某种产品,如果生产一件甲等品可获利50元,生产一件乙等品可获利30元,生产一件次品,要赔20元,已知这台机器生产甲等品、乙等品和次品的概率分别为0.6、0.3和0.1,则这台机器每生产一件产品,平均预期可获得( )
A.36元 B.37元
C.38元 D.39元
5.一牧场有10头牛,因误食含有病毒的饲料而被感染,已知该病的发病率为0.02.设发病的牛的头数为ξ,则Dξ等于( )
A.0.2 B.0.8 C.0.196 D.0.804
6.甲、乙两台自动车床生产同种标准件,X表示甲机床生产1 000件产品中的次品数,Y表示乙机床生产1 000件产品中的次品数,经过一段时间的考查,X、Y的分布列分别为
X
0
1
2
3
P
0.7
0.1
0.1
0.1
Y
0
1
2
3
P
0.5
0.3
0.2
0
据此判断( )
A.甲比乙质量好 B.乙比甲质量好
C.甲与乙质量相同 D.无法判定
7.某种种子每粒发芽的概率都为0.9,现播种了1 000粒,对于没有发芽的种子,每粒需再补种2粒,补种的种子数记为X,则X的均值为( )
A.100 B.200 C.300 D.400
8.甲、乙、丙三名射箭运动员在某次测试中各射箭20次,三人的测试成绩如下表:
41211570485甲的成绩
环数
7
8
9
10
频数
5
5
5
5
乙的成绩
环数
7
8
9
10
频数
6
4
4
6
丙的成绩
环数
7
8
9
10
频数
4
6
6
4
甲的成绩
环数
7
8
9
10
频数
5
5
5
5
乙的成绩
环数
7
8
9
10
频数
6
4
4
6
丙的成绩
环数
7
8
9
10
频数
4
6
6
4
s1,s2,s3分别表示甲、乙、丙三名运动员这次测试成绩的标准差,则有( ).
A.s3>s1>s2 B.s2>s1>s3 C.s1>s2>s3 D.s2>s3>s1
二、填空题
9.有两台自动包装机甲与乙,包装重量分别为随机变量ξ1、ξ2,若Eξ1=Eξ2,Dξ1>Dξ2,则自动包装机________的质量较好.
10.随机变量ξ的分布列如下:
ξ
-1
0
1
P
a
b
c
其中a,b,c成等差数列.若,则D(ξ)的值是________.
11.节日期间,某种鲜花进货价是每束2.5元,销售价是每束5元;节后卖不出的鲜花以每束1.6元处理,根据前五年销售情况预测,节日期间这种鲜花的需求量X服从如表所示的概率分布:
X
200
300
400
500
P
0.20
0.35
0.30
0.15
若进这种鲜花500束,则期望利润是________元.
12.某射手有5发子弹,射击一次,命中率是0.9,如果命中了就停止射击,否则一直射到子弹用尽为止,设损耗子弹数为X,则E(X)=________,D(X)=________.(精确到0.01)
三、解答题
13. 已知盒中有10个灯泡,其中8个正品,2个次品需要从中取出2个正品,每次取出1个,取出后不放回,直到取出2个正品为止设ξ为取出的次数,求ξ的分布列及Eξ
14.设在12个同类型的零件中有2个次品,抽取3次进行检验,每次抽取一个,并且取出后不再放回,若以X和V分别表示取出次品和正品的个数.
(1)求X的概率分布、期望值及方差;
(2)求Y的概率分布、期望值及方差.
15.有甲、乙两个建材厂,都想投标参加某重点建设,为了对重点建设负责,政府到两建材厂抽样检查,他们从中各取等量的样品:检查它们的抗拉强度指数如下:
ξ
110
120
125
130
135
P
0.1
0.2
0.4
0.1
0.2
η
100
115
125
130
145
P
0.1
0.2
0.4
0.1
0.2
其中ξ和η分别表示甲、乙两厂材料的抗拉强度,在要求抗拉强度不低于120的条件下,比较甲、乙两厂材料哪一种稳定性较好.
【答案与解析】
1.【答案】 C
【解析】 由0.1+a+b+0.1=1,得a+b=0.8,①
又由E(X)=0×0.1+1×a+2×b+3×0.1=1.6,
得a+2b=1.3,②
由①②解得a=0.3,b=0.5,∴a-b=-0.2,故应选C.
2. 【答案】D
【解析】ξ~B(l,q),p+q=1.
3. 【答案】 A
【解析】 E(X)=(1+2+3)×=2,
D(X)=[(1-2)2+(2-2)2+(3-2)2]×=23,
∴D(3X+5)=9D(X)=6.
4. 【答案】B
【解析】由题意知每生产一件产品,平均预期可获利0.6×50+0.3×30+0.1×(-20)=37(元).
5. 【答案】C
【解析】根据二项分布的方差公式:Dξ=10×0.02×0.98=0.196.
6. 【答案】A
【解析】EX=0.7×0+1×0.1+2×0.1+3×0.1=0.6,
EY=0×0.5+1×0.3+2×0.2+3×0=0.7,
因为EX
【解析】 本题以实际问题为背景,考查的事件的均值问题.
记“不发芽的种子数为ξ”,则ξ~B(1 000,0.1),所以E(ξ)=1 000×0.1=100,而X=2ξ,故EX=E(2ξ)=2E(ξ)=200,故选B.
8.【答案】B
【解析】 设甲、乙、丙射中的环数依次为X1、X2、X3。依题意对甲有:
X1
7
8
9
10
P
,
,;
对乙有:
X2
7
8
9
10
P
,
,;同理可得。故s2>s1>s3。
9. 【答案】乙
【解析】Eξ1=Eξ2说明甲、乙两机包装的重量的平均水平一样.Dξ1>Dξ2说明甲机包装重量的差别大,不稳定.∴乙机质量好.
10.【答案】
【解析】 依随机变量的分布列知a+b+c=1,
依a,b,c成等差数列知2b=a+c,则,。
又,则。
解得,,。
故。
11.【答案】706
【解析】 节日期间鲜花预售量为
E(X)=200×0.20+300×0.35+400×0.30+500×0.15=40+105+120+75=340,
则期望的利润Y=5X+1.6(500―X)―500×2.5=3.4X―450,
∴E(Y)=3.4 E(X)―450=3.4×340―450=706。
故期望利润为706元。
12.【答案】1.11 0.12
【解析】随机变量X服从超几何分布,根据公式:期望方差可求。
13. 【解析】
每次取1件产品,∴至少需2次,即ξ最小为2,有2件次品,当前2次取得的都是次品时,ξ=4,所以ξ可以取2,3,4
P(ξ=2)=×=;
P(ξ=3)=××+××=;P(ξ=4)=1--=
∴ξ的分布列如下:
ξ
2
3
4
P
Eξ=2×P(ξ=2)+3×P(ξ=3)+4×P(ξ=4)=
14.【解析】(1)X的可能取值为0,1,2。
若X=0,表示没有取出次品,其概率为,
同理,有,。
∴X的概率分布为
X
0
1
2
P
∴,
D(。
(2)Y的可能取值为1,2,3,显然X+Y=3。
,,
。
∴Y的概率分布为
Y
1
2
3
P
∴。
∵Y=-X+3,∴。
15.【解析】
E(ξ)=110×0.1+120×0.2+125×0.4+130×0.1+135×0.2=125,
E(η)=100×0.1+115×0.2+125×0.4+130×0.1+145×0.2=125,
D(ξ)=0.1×(110-125)2+0.2×(120-125)2+0.4×(125-125)2+0.1×(130-125)2+0.2-(135-125)2=50,
D(η)=0.1×(100-125)2+0.2×(115-125)2+0.4×(125-125)2+0.1×(130-125)2+0.2×(145-125)2=165,
由于E(ξ)=E(η),而D(ξ)<D(η),
故甲厂的材料稳定性较好。
