【新教材】模块综合测评-人教B版(2019)高中数学选择性必修第二册练习(Word含解析)
文档属性
| 名称 | 【新教材】模块综合测评-人教B版(2019)高中数学选择性必修第二册练习(Word含解析) | 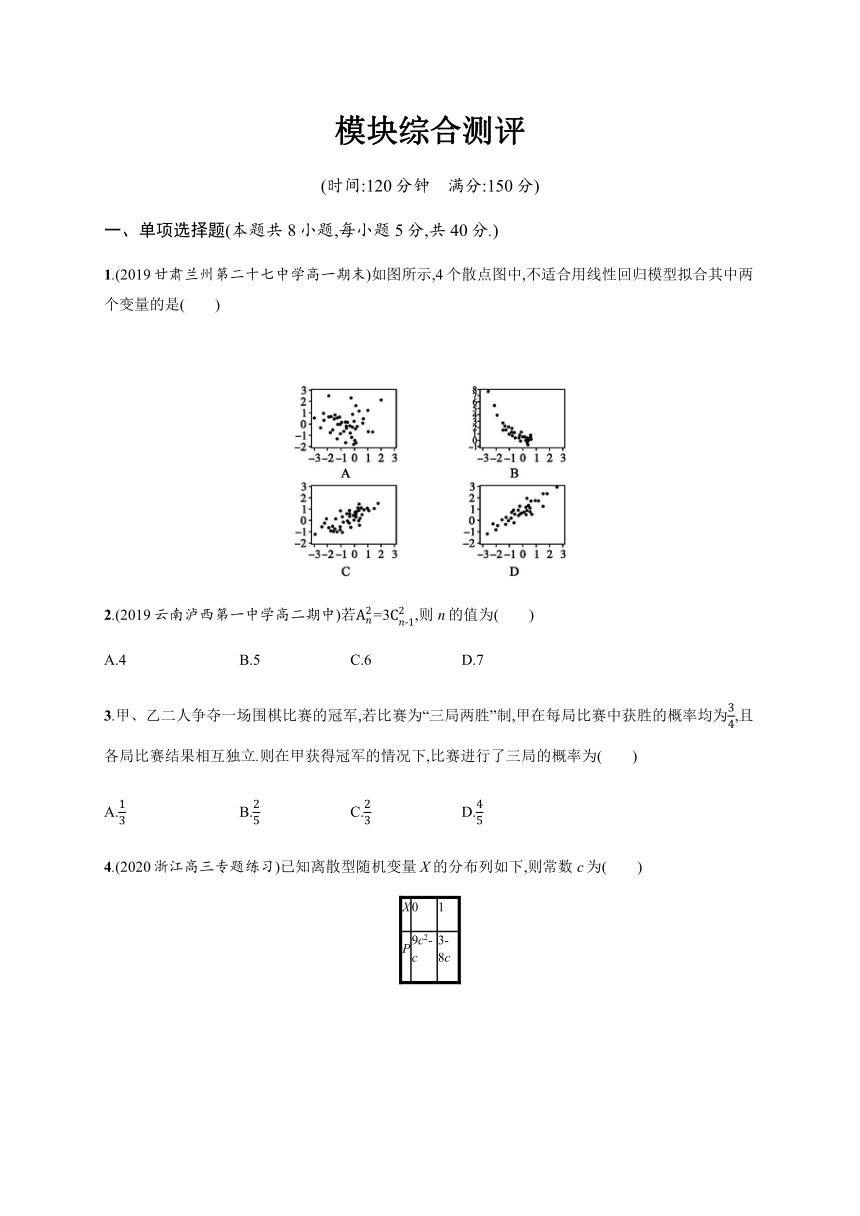 | |
| 格式 | docx | ||
| 文件大小 | 163.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-30 22:58:48 | ||
图片预览





文档简介
1228090011595100模块综合测评
(时间:120分钟 满分:150分)
一、单项选择题(本题共8小题,每小题5分,共40分.)
1.(2019甘肃兰州第二十七中学高一期末)如图所示,4个散点图中,不适合用线性回归模型拟合其中两个变量的是( )
2.(2019云南泸西第一中学高二期中)若An2=3Cn-12,则n的值为( )
A.4 B.5 C.6 D.7
3.甲、乙二人争夺一场围棋比赛的冠军,若比赛为“三局两胜”制,甲在每局比赛中获胜的概率均为34,且各局比赛结果相互独立.则在甲获得冠军的情况下,比赛进行了三局的概率为( )
A.13 B.25 C.23 D.45
4.(2020浙江高三专题练习)已知离散型随机变量X的分布列如下,则常数c为( )
X
0
1
P
9c2-c
3-8c
A.13 B.23 C.13或23 D.14
5.(2019天津高三期中)两个实习生每人加工一个零件.加工为一等品的概率分别为56和34,两个零件是否加工为一等品相互独立,则这两个零件中恰有一个一等品的概率为( )
A.12 B.13 C.512 D.16
6.(2019重庆高二期末)若随机变量X~B(n,p),其均值是80,标准差是4,则n和p的值分别是( )
A.100,0.2 B.200,0.4
C.100,0.8 D.200,0.6
7.已知随机变量X服从正态分布N(100,4),若P(m [附:P(μ-σ≤X≤μ+σ)≈68.3%,P(μ-2σ≤X≤μ+2σ)≈95.4%]
A.100 B.101 C.102 D.103
8.(2020江西高安中学高二期末)某校在“数学联赛”考试后选取了6名教师参加阅卷,试卷共4道解答题,要求将这6名教师分成4组,每组改一道解答题,其中2组各有2名教师,另外2组各有1名教师,则不同的分配方案的种数是( )
A.216 B.420 C.720 D.1 080
二、多项选择题(本题共4小题,每小题5分,共20分)
9.(2019山东高三月考)x+124x8展开式中系数最大的项可以为( )
A.第2项 B.第3项
C.第4项 D.第5项
10.若随机变量ξ的分布列如下表所示,其中m∈(0,1),则下列结果中正确的是( )
ξ
0
1
P
m
n
A.E(ξ)=m B.D(ξ)=n2
C.E(ξ)=1-m D.D(ξ)=m-m2
11.(2019河北高二期中)下面四个选项中,正确的是( )
A.设a,b,c分别表示数据15,17,14,10,15,17,17,16,14,12的平均数、中位数、众数,则a B.在线性回归模型中,相关系数r的绝对值越接近于1,表示两个变量的相关性越强
C.绘制频率分布直方图时,各小长方形的面积等于相应各组的组距
D.线性回归直线不一定过样本中心点(x,y)
12.一袋中有大小相同的4个红球和2个白球,给出下列结论:
①从中任取3球,恰有一个白球的概率是35;
②从中有放回的取球6次,每次任取一球,则取到红球次数的方差为43;
③现从中不放回的取球2次,每次任取1球,则在第一次取到红球的条件下,第二次再次取到红球的概率为25;
④从中有放回的取球3次,每次任取一球,则至少有一次取到红球的概率为2627.
其中正确的选项是( )
A.① B.② C.③ D.④
三、填空题(本题共4小题,每小题5分,共20分)
13.(2019上海大同中学高三月考)某中学的汪老师在教室进行第二轮复习时布置了两道填空题,他预测学生做对第一题的概率为0.8,两题全对的概率为0.6,则汪老师预测第二题正确的概率为 .?
14.(2019河南高三月考)将一颗质地均匀的骰子(一种各个面上分别标有1,2,3,4,5,6个点的正方体玩具)先后抛掷2次,则出现向上的点数之和为奇数的概率是 .?
15.(2020浙江高三专题练习)一个口袋里装有大小相同的5个小球,其中红色2个,其余3个颜色各不相同.现从中任意取出3个小球,其中恰有2个小球颜色相同的概率是 ;若变量X为取出的3个小球中红球的个数,则X的数学期望E(X)= .?
16.已知随机变量ξ~B(36,p),且E(ξ)=12,则D(4ξ+3)= .?
四、解答题(本题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤)
17.(10分)(2019上海金山中学高二月考)(1)若ax?x29的二项展开式中x3的系数为94,求实数a的值;
(2)若(3x-1)7=a7x7+a6x6+…+a1x+a0,求a1+a3+a5+a7.
18.(12分)(2020辽宁高三期末)足球是世界普及率最高的运动,我国大力发展校园足球.为了解本地区足球特色学校的发展状况,社会调查小组得到如下统计数据:
年份x
2014
2015
2016
2017
2018
足球特色学校y/百个
0.30
0.60
1.00
1.40
1.70
(1)根据上表数据,计算y与x的相关系数r,并说明y与x的线性相关性强弱;
(已知:0.75≤|r|≤1,则认为y与x线性相关性很强;0.3≤|r|<0.75,则认为y与x线性相关性一般;|r|≤0.25,则认为y与x线性相关性较弱)
(2)求y关于x的线性回归方程,并预测该地区2020年足球特色学校的个数(精确到个).
参考公式和数据:r=∑i=1n(xi-x)(yi-y)∑i=1n(xi-x)2∑i=1n(yi-y)2,∑i=15(xi-x)2=10,∑i=15(yi-y)2=1.3,13≈3.605 6,b^=∑i=1n(xi-x)(yi-y)∑i=1n(xi-x)2,a^=y?b^x.
19.(12分)(2019天津高考)设甲、乙两位同学上学期间,每天7:30之前到校的概率均为23.假定甲、乙两位同学到校情况互不影响,且任一同学每天到校情况相互独立.
(1)用X表示甲同学上学期间的三天中7:30之前到校的天数,求随机变量X的分布列和数学期望;
(2)设M为事件“上学期间的三天中,甲同学在7:30之前到校的天数比乙同学在7:30之前到校的天数恰好多2”,求事件M发生的概率.
20.(12分)(2020山东高三期末)读书可以使人保持思想活力,让人得到智慧启发,让人滋养浩然正气.书籍是文化的重要载体,读书是承继文化的重要方式.某地区为了解学生课余时间的读书情况,随机抽取了n名学生进行调查,根据调查得到的学生日均课余读书时间绘制成如图所示的频率分布直方图,将日均课余读书时间不低于40分钟的学生称为“读书之星”,日均课余读书时间低于40分钟的学生称为“非读书之星”.已知抽取的样本中日均课余读书时间低于10分钟的有10人.
(1)求n,p的值;
(2)根据已知条件完成下面的2×2列联表,并判断是否有95%以上的把握认为“读书之星”与性别有关?
非读书之星
读书之星
总计
男
女
10
55
总计
(3)将上述调查所得到的频率视为概率,现从该地区大量学生中,随机抽取3名学生,每次抽取1名,已知每个人是否被抽到互不影响,记被抽取的“读书之星”人数为随机变量X,求X的分布列和期望.
附:χ2=n(ad-bc)2(a+b)(c+d)(a+c)(b+d),其中n=a+b+c+d.
P(χ2≥k)
0.10
0.05
0.025
0.010
0.005
0.001
k
2.706
3.841
5.024
6.635
7.879
10.828
21.(12分)(2019天津高三月考)某校为了普及环保知识,增强学生的环保意识,在全校组织了一次有关环保知识的竞赛.经过初赛、复赛,甲、乙两个代表队(每队3人)进入了决赛,规定每人回答一个问题,答对为本队赢得10分,答错得0分.假设甲队中每人答对的概率均为34,乙队中3人答对的概率分别为45,34,23,且各人回答正确与否相互之间没有影响,用ξ表示乙队的总得分.
(1)求ξ的分布列及数学期望;
(2)求甲、乙两队总得分之和等于30分且甲队获胜的概率.
22.(12分)(2019青海高三月考)某企业打算处理一批产品,这些产品每箱100件,以箱为单位销售.已知这批产品中每箱出现的废品率只有10%或者20%两种可能,两种可能对应的概率均为0.5.假设该产品正品每件市场价格为100元,废品不值钱.现处理价格为每箱8 400元,遇到废品不予更换.以一箱产品中正品的价格期望值作为决策依据.
(1)在不开箱检验的情况下,判断是否可以购买;
(2)现允许开箱,有放回地随机从一箱中抽取2件产品进行检验.
①若此箱出现的废品率为20%,记抽到的废品数为X,求X的分布列和数学期望;
②若已发现在抽取检验的2件产品中,其中恰有一件是废品,判断是否可以购买.
1228090011595100模块综合测评
(时间:120分钟 满分:150分)
一、单项选择题(本题共8小题,每小题5分,共40分.)
1.(2019甘肃兰州第二十七中学高一期末)如图所示,4个散点图中,不适合用线性回归模型拟合其中两个变量的是( )
解析根据题意,适合用线性回归拟合其中两个变量的散点图必须散点分布比较集中,且大体接近某一条直线,分析选项可得A选项的散点图杂乱无章,最不符合条件.故选A.
答案A
2.(2019云南泸西第一中学高二期中)若An2=3Cn-12,则n的值为( )
A.4 B.5 C.6 D.7
解析因为An2=3Cn-12,所以n(n-1)=3(n-1)(n-2)2,解得n=6或n=1(舍去).故选C.
答案C
3.甲、乙二人争夺一场围棋比赛的冠军,若比赛为“三局两胜”制,甲在每局比赛中获胜的概率均为34,且各局比赛结果相互独立.则在甲获得冠军的情况下,比赛进行了三局的概率为( )
A.13 B.25 C.23 D.45
解析记事件A:甲获得冠军,事件B:比赛进行三局,
事件AB:甲获得冠军,且比赛进行了三局,则第三局甲胜,前两局甲胜了一局,
由独立事件的概率乘法公式得P(AB)=C21×34×14×34=932,
对于事件A,甲获得冠军,包含两种情况:前两局甲胜和事件AB,
所以P(A)=342+932=2732,
所以P(B|A)=P(AB)P(A)=932×3227=13,故选A.
答案A
4.(2020浙江高三专题练习)已知离散型随机变量X的分布列如下,则常数c为( )
X
0
1
P
9c2-c
3-8c
A.13 B.23 C.13或23 D.14
解析由随机变量的分布列知,9c2-c≥0,3-8c≥0,9c2-c+3-8c=1,
所以c=13,故选A.
答案A
5.(2019天津高三期中)两个实习生每人加工一个零件.加工为一等品的概率分别为56和34,两个零件是否加工为一等品相互独立,则这两个零件中恰有一个一等品的概率为( )
A.12 B.13 C.512 D.16
解析记两个零件中恰好有一个一等品的事件为A,即仅第一个实习生加工一等品为事件A1,仅第二个实习生加工一等品为事件A2两种情况,则P(A)=P(A1)+P(A2)=56×14+16×34=13.故选B.
答案B
6.(2019重庆高二期末)若随机变量X~B(n,p),其均值是80,标准差是4,则n和p的值分别是( )
A.100,0.2 B.200,0.4
C.100,0.8 D.200,0.6
解析∵随机变量X~B(n,p),其均值是80,标准差是4,∴由np=80,np(1-p)=16,∴p=0.8,n=100.故选C.
答案C
7.已知随机变量X服从正态分布N(100,4),若P(m [附:P(μ-σ≤X≤μ+σ)≈68.3%,P(μ-2σ≤X≤μ+2σ)≈95.4%]
A.100 B.101 C.102 D.103
解析由题意,知P(μ-σ≤X≤μ+σ)=0.683,P(μ-2σ≤X≤μ+2σ)=0.954,
则P(μ-2σ≤X≤μ+2σ)-P(μ-σ≤X≤μ+σ)2=0.954-0.6832=0.135 5,
所以要使得P(m 答案C
8.(2020江西高安中学高二期末)某校在“数学联赛”考试后选取了6名教师参加阅卷,试卷共4道解答题,要求将这6名教师分成4组,每组改一道解答题,其中2组各有2名教师,另外2组各有1名教师,则不同的分配方案的种数是( )
A.216 B.420 C.720 D.1 080
解析6人分成4组共有C62C422种不同的分组方案,所以共有C62C422A44=15×62×24=1 080种不同的分配方案.
答案D
二、多项选择题(本题共4小题,每小题5分,共20分)
9.(2019山东高三月考)x+124x8展开式中系数最大的项可以为( )
A.第2项 B.第3项
C.第4项 D.第5项
解析x+124x8的展开式的通项公式为Tk+1=C8k·(x)8-k·124xk=12k·C8k·x4-34k,
其展开式的各项系数依次为1,4,7,7,358,74,716,116,1256,
所以,展开式中系数最大的项是第3项和第4项.
故选BC.
答案BC
10.若随机变量ξ的分布列如下表所示,其中m∈(0,1),则下列结果中正确的是( )
ξ
0
1
P
m
n
A.E(ξ)=m B.D(ξ)=n2
C.E(ξ)=1-m D.D(ξ)=m-m2
解析由离散型随机变量的概率关系可知:n=1-m.
则E(ξ)=0×m+1×n=n=1-m;
D(ξ)=[0-(1-m)]2m+[1-(1-m)]2(1-m)=m-m2=n-n2.
答案CD
11.(2019河北高二期中)下面四个选项中,正确的是( )
A.设a,b,c分别表示数据15,17,14,10,15,17,17,16,14,12的平均数、中位数、众数,则a B.在线性回归模型中,相关系数r的绝对值越接近于1,表示两个变量的相关性越强
C.绘制频率分布直方图时,各小长方形的面积等于相应各组的组距
D.线性回归直线不一定过样本中心点(x,y)
解析对于A,根据数据可求得平均数为a=15+17+14+10+15+17+17+16+14+1210=14710=14.7,从小到大排列可得10,12,14,14,15,15,16,17,17,17,所以中位数为b=15,由数据可知众数为c=17,即a 对于B,根据相关系数的意义,可知当相关系数r的绝对值越接近于1,表示两个变量的相关性越强,所以B正确;
对于C,绘制频率分布直方图时,各小长方形的面积等于相应各组的频率,所以C错误;
对于D,根据线性回归方程中a^的求法,可知必过样本中心点(x,y),所以D错误.
故选AB.
答案AB
12.一袋中有大小相同的4个红球和2个白球,给出下列结论:
①从中任取3球,恰有一个白球的概率是35;
②从中有放回的取球6次,每次任取一球,则取到红球次数的方差为43;
③现从中不放回的取球2次,每次任取1球,则在第一次取到红球的条件下,第二次再次取到红球的概率为25;
④从中有放回的取球3次,每次任取一球,则至少有一次取到红球的概率为2627.
其中正确的选项是( )
A.① B.② C.③ D.④
解析①从中任取3个球,恰有一个白球的概率是C21C42C63=35,故A正确;
②从中有放回地取球6次,每次任取一球,取到红球次数X~B6,23,其方差为6×23×1-23=43,故B正确;
③从中不放回地取球2次,每次任取一球,则在第一次取到红球后,此时袋中还有3个红球和2个白球,则第二次再次取到红球的概率为35,故C错误;
④从中有放回地取球3次,每次任取一球,每次取到红球的概率为P=23,所以至少有一次取到红球的概率为1-1-233=2627,故D正确.故选ABD.
答案ABD
三、填空题(本题共4小题,每小题5分,共20分)
13.(2019上海大同中学高三月考)某中学的汪老师在教室进行第二轮复习时布置了两道填空题,他预测学生做对第一题的概率为0.8,两题全对的概率为0.6,则汪老师预测第二题正确的概率为 .?
解析设“做对第一道题”为事件A,“做对第二道题”为事件B,
则P(AB)=P(A)P(B)=0.8·P(B)=0.6,
所以P(B)=0.75.
答案0.75
14.(2019河南高三月考)将一颗质地均匀的骰子(一种各个面上分别标有1,2,3,4,5,6个点的正方体玩具)先后抛掷2次,则出现向上的点数之和为奇数的概率是 .?
解析骰子先后投掷2次,所有可能的结果种数共有C61C61=36种.
∵奇数与偶数之和为奇数,
∴向上的点数之和为奇数的结果种数有2C31C31=18种,∴向上的点数之和为奇数的概率P=1836=12.
答案12
15.(2020浙江高三专题练习)一个口袋里装有大小相同的5个小球,其中红色2个,其余3个颜色各不相同.现从中任意取出3个小球,其中恰有2个小球颜色相同的概率是 ;若变量X为取出的3个小球中红球的个数,则X的数学期望E(X)= .?
解析一个口袋里装有大小相同的5个小球,其中红色2个,其余3个颜色各不相同.
现从中任意取出3个小球,
基本事件总数n=C53=10,
其中恰有2个小球颜色相同包含的基本事件个数m=C22C31=3,所以其中恰有2个小球颜色相同的概率是P=mn=310.
变量X为取出的3个小球中红球的个数,则X的可能取值为0,1,2,
P(X=0)=C33C53=110,
P(X=1)=C21C32C53=610=35,
P(X=2)=C22C31C53=310,
数学期望E(X)=0×110+1×610+2×310=65.
答案310 65
16.已知随机变量ξ~B(36,p),且E(ξ)=12,则D(4ξ+3)= .?
解析随机变量ξ~B(36,p),且E(ξ)=12,
所以n=36,且np=36p=12,解得p=13,
所以D(ξ)=np(1-p)=36×13×23=8,
所以D(4ξ+3)=42D(ξ)=16×8=128.
答案128
四、解答题(本题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤)
17.(10分)(2019上海金山中学高二月考)(1)若ax?x29的二项展开式中x3的系数为94,求实数a的值;
(2)若(3x-1)7=a7x7+a6x6+…+a1x+a0,求a1+a3+a5+a7.
解(1)ax?x29的二项展开式通项为Tk+1=C9kax9-k-x2k=-12ka9-kC9kx3k-182,
当3k-182=3,即k=8时,T9=-128aC98x3=9a16x3.
又x3的系数为94,∴9a16=94,解得a=4.
(2)令x=1,得a7+a6+a5+a4+a3+a2+a1+a0=27,①
令x=-1,得-a7+a6-a5+a4-a3+a2-a1+a0=-47,②
①-②,得2a7+2a5+2a3+2a1=27+47=16 512,
∴a1+a3+a5+a7=8 256.
18.(12分)(2020辽宁高三期末)足球是世界普及率最高的运动,我国大力发展校园足球.为了解本地区足球特色学校的发展状况,社会调查小组得到如下统计数据:
年份x
2014
2015
2016
2017
2018
足球特色学校y/百个
0.30
0.60
1.00
1.40
1.70
(1)根据上表数据,计算y与x的相关系数r,并说明y与x的线性相关性强弱;
(已知:0.75≤|r|≤1,则认为y与x线性相关性很强;0.3≤|r|<0.75,则认为y与x线性相关性一般;|r|≤0.25,则认为y与x线性相关性较弱)
(2)求y关于x的线性回归方程,并预测该地区2020年足球特色学校的个数(精确到个).
参考公式和数据:r=∑i=1n(xi-x)(yi-y)∑i=1n(xi-x)2∑i=1n(yi-y)2,∑i=15(xi-x)2=10,∑i=15(yi-y)2=1.3,13≈3.605 6,b^=∑i=1n(xi-x)(yi-y)∑i=1n(xi-x)2,a^=y?b^x.
解(1)由题得x=2 016,y=1,所以r=∑i=15(xi-x)(yi-y)∑i=15(xi-x)2∑i=15(yi-y)2=3.610×1.3
=3.63.605 6≈0.998>0.7,
故y与x线性相关性很强.
(2)b^=∑i=15(xi-x)(yi-y)∑i=15(xi-x)2=
(-2)×(-0.7)+(-1)×(-0.4)+1×0.4+2×0.74+1+0+1+4
=0.36,
a^=y?b^x=1-2 016×0.36=-724.76,
∴y关于x的线性回归方程是y^=0.36x-724.76.
当x=2 020时,y^=0.36x-724.76=2.44,
即该地区2020年足球特色学校有244个.
19.(12分)(2019天津高考)设甲、乙两位同学上学期间,每天7:30之前到校的概率均为23.假定甲、乙两位同学到校情况互不影响,且任一同学每天到校情况相互独立.
(1)用X表示甲同学上学期间的三天中7:30之前到校的天数,求随机变量X的分布列和数学期望;
(2)设M为事件“上学期间的三天中,甲同学在7:30之前到校的天数比乙同学在7:30之前到校的天数恰好多2”,求事件M发生的概率.
解(1)因为甲同学上学期间的三天中到校情况相互独立,且每天7:30之前到校的概率均为23,故X~B3,23,从而P(X=k)=C3k23k133-k,k=0,1,2,3.
所以,随机变量X的分布列为
X
0
1
2
3
P
127
29
49
827
随机变量X的数学期望E(X)=3×23=2.
(2)设乙同学上学期间的三天中7:30之前到校的天数为Y,则Y~B3,23,且M={X=3,Y=1}∪{X=2,Y=0}.由题意知事件{X=3,Y=1}与{X=2,Y=0}互斥,且事件{X=3}与{Y=1},事件{X=2}与{Y=0}均相互独立,从而由(1)知P(M)=P({X=3,Y=1}∪{X=2,Y=0})=P(X=3,Y=1)+P(X=2,Y=0)=P(X=3)P(Y=1)+P(X=2)P(Y=0)=827×29+49×127=20243.
20.(12分)(2020山东高三期末)读书可以使人保持思想活力,让人得到智慧启发,让人滋养浩然正气.书籍是文化的重要载体,读书是承继文化的重要方式.某地区为了解学生课余时间的读书情况,随机抽取了n名学生进行调查,根据调查得到的学生日均课余读书时间绘制成如图所示的频率分布直方图,将日均课余读书时间不低于40分钟的学生称为“读书之星”,日均课余读书时间低于40分钟的学生称为“非读书之星”.已知抽取的样本中日均课余读书时间低于10分钟的有10人.
(1)求n,p的值;
(2)根据已知条件完成下面的2×2列联表,并判断是否有95%以上的把握认为“读书之星”与性别有关?
非读书之星
读书之星
总计
男
女
10
55
总计
(3)将上述调查所得到的频率视为概率,现从该地区大量学生中,随机抽取3名学生,每次抽取1名,已知每个人是否被抽到互不影响,记被抽取的“读书之星”人数为随机变量X,求X的分布列和期望.
附:χ2=n(ad-bc)2(a+b)(c+d)(a+c)(b+d),其中n=a+b+c+d.
P(χ2≥k)
0.10
0.05
0.025
0.010
0.005
0.001
k
2.706
3.841
5.024
6.635
7.879
10.828
解(1)(0.005+p+0.018+0.020+0.022+0.025)×10=1,解得p=0.01,所以n=100.1=100.
(2)因为n=100,所以“读书之星”有100×0.25=25.从而2×2列联表如下表所示
非读书之星
读书之星
总计
男
30
15
45
女
45
10
55
总计
75
25
100
将2×2列联表中的数据代入公式计算得
χ2=100×(30×10-15×45)245×55×75×25=10033≈3.030,
因为3.030<3.841,所以没有95%以上的把握认为“读书之星”与性别有关.
(3)将频率视为概率,即从该地区学生中抽取一名学生是“读书之星”的概率为14.
由题意可知X~B3,14,
所以P(X=0)=C30×140×1-143=2764,
P(X=1)=C31×14×1-142=2764,
P(X=2)=C32×142×1-14=964,
P(X=3)=C33×143=164,
所以X的分布列为
X
0
1
2
3
P
2764
2764
964
164
故E(X)=3×14=34.
21.(12分)(2019天津高三月考)某校为了普及环保知识,增强学生的环保意识,在全校组织了一次有关环保知识的竞赛.经过初赛、复赛,甲、乙两个代表队(每队3人)进入了决赛,规定每人回答一个问题,答对为本队赢得10分,答错得0分.假设甲队中每人答对的概率均为34,乙队中3人答对的概率分别为45,34,23,且各人回答正确与否相互之间没有影响,用ξ表示乙队的总得分.
(1)求ξ的分布列及数学期望;
(2)求甲、乙两队总得分之和等于30分且甲队获胜的概率.
解(1)由题意知,ξ的所有可能取值为0,10,20,30.
P(ξ=0)=15×14×13=160;
P(ξ=10)=45×14×13+15×34×13+15×14×23=960=320;
P(ξ=20)=45×34×13+45×14×23+15×34×23=2660=1330;
P(ξ=30)=45×34×23=2460=25.
∴ξ的分布列为
ξ
0
10
20
30
P
160
320
1330
25
∴E(ξ)=0×160+10×320+20×1330+30×25=1336.
(2)用A表示“甲得30分乙得0分”,用B表示“甲得20分乙得10分”,且A,B互斥,
又P(A)=343×160=91 280,P(B)=C32342×14×320=811 280,甲、乙两队得分总和为30分且甲获胜的概率为P(A+B)=P(A)+P(B)=901 280=9128.
22.(12分)(2019青海高三月考)某企业打算处理一批产品,这些产品每箱100件,以箱为单位销售.已知这批产品中每箱出现的废品率只有10%或者20%两种可能,两种可能对应的概率均为0.5.假设该产品正品每件市场价格为100元,废品不值钱.现处理价格为每箱8 400元,遇到废品不予更换.以一箱产品中正品的价格期望值作为决策依据.
(1)在不开箱检验的情况下,判断是否可以购买;
(2)现允许开箱,有放回地随机从一箱中抽取2件产品进行检验.
①若此箱出现的废品率为20%,记抽到的废品数为X,求X的分布列和数学期望;
②若已发现在抽取检验的2件产品中,其中恰有一件是废品,判断是否可以购买.
解(1)在不开箱检验的情况下,一箱产品中正品的价格期望值为E(ξ)=100×(1-0.2)×100×0.5+100×(1-0.1)×100×0.5=8 500>8 400,
∴在不开箱检验的情况下,可以购买.
(2)①X的可能取值为0,1,2,
P(X=0)=C20×0.20×0.82=0.64,
P(X=1)=C21×0.21×0.81=0.32,
P(X=2)=C22×0.22×0.80=0.04,
∴X的分布列为
X
0
1
2
P
0.64
0.32
0.04
E(X)=0×0.64+1×0.32+2×0.04=0.4.
②设事件A:发现在抽取检验的2件产品中,其中恰有一件是废品,
则P(A)=C21×0.2×0.8×0.5+C21×0.1×0.9×0.5=0.25,一箱产品中,设正品的价格的期望值为η,则η=8 000,9 000,
事件B1:抽取的废品率为20%的一箱,
则P(η=8 000)=P(B1|A)=P(AB1)P(A)=C21×0.2×0.8×0.50.25=0.64,
事件B2:抽取的废品率为10%的一箱,
则P(η=9 000)=P(B2|A)=P(AB2)P(A)=C21×0.1×0.9×0.50.25=0.36,∴E(η)=8 000×0.64+9 000×0.36=8 360<8 400,∴已发现在抽取检验的2件产品中,其中恰有一件是废品,则不可以购买.
(时间:120分钟 满分:150分)
一、单项选择题(本题共8小题,每小题5分,共40分.)
1.(2019甘肃兰州第二十七中学高一期末)如图所示,4个散点图中,不适合用线性回归模型拟合其中两个变量的是( )
2.(2019云南泸西第一中学高二期中)若An2=3Cn-12,则n的值为( )
A.4 B.5 C.6 D.7
3.甲、乙二人争夺一场围棋比赛的冠军,若比赛为“三局两胜”制,甲在每局比赛中获胜的概率均为34,且各局比赛结果相互独立.则在甲获得冠军的情况下,比赛进行了三局的概率为( )
A.13 B.25 C.23 D.45
4.(2020浙江高三专题练习)已知离散型随机变量X的分布列如下,则常数c为( )
X
0
1
P
9c2-c
3-8c
A.13 B.23 C.13或23 D.14
5.(2019天津高三期中)两个实习生每人加工一个零件.加工为一等品的概率分别为56和34,两个零件是否加工为一等品相互独立,则这两个零件中恰有一个一等品的概率为( )
A.12 B.13 C.512 D.16
6.(2019重庆高二期末)若随机变量X~B(n,p),其均值是80,标准差是4,则n和p的值分别是( )
A.100,0.2 B.200,0.4
C.100,0.8 D.200,0.6
7.已知随机变量X服从正态分布N(100,4),若P(m
A.100 B.101 C.102 D.103
8.(2020江西高安中学高二期末)某校在“数学联赛”考试后选取了6名教师参加阅卷,试卷共4道解答题,要求将这6名教师分成4组,每组改一道解答题,其中2组各有2名教师,另外2组各有1名教师,则不同的分配方案的种数是( )
A.216 B.420 C.720 D.1 080
二、多项选择题(本题共4小题,每小题5分,共20分)
9.(2019山东高三月考)x+124x8展开式中系数最大的项可以为( )
A.第2项 B.第3项
C.第4项 D.第5项
10.若随机变量ξ的分布列如下表所示,其中m∈(0,1),则下列结果中正确的是( )
ξ
0
1
P
m
n
A.E(ξ)=m B.D(ξ)=n2
C.E(ξ)=1-m D.D(ξ)=m-m2
11.(2019河北高二期中)下面四个选项中,正确的是( )
A.设a,b,c分别表示数据15,17,14,10,15,17,17,16,14,12的平均数、中位数、众数,则a
C.绘制频率分布直方图时,各小长方形的面积等于相应各组的组距
D.线性回归直线不一定过样本中心点(x,y)
12.一袋中有大小相同的4个红球和2个白球,给出下列结论:
①从中任取3球,恰有一个白球的概率是35;
②从中有放回的取球6次,每次任取一球,则取到红球次数的方差为43;
③现从中不放回的取球2次,每次任取1球,则在第一次取到红球的条件下,第二次再次取到红球的概率为25;
④从中有放回的取球3次,每次任取一球,则至少有一次取到红球的概率为2627.
其中正确的选项是( )
A.① B.② C.③ D.④
三、填空题(本题共4小题,每小题5分,共20分)
13.(2019上海大同中学高三月考)某中学的汪老师在教室进行第二轮复习时布置了两道填空题,他预测学生做对第一题的概率为0.8,两题全对的概率为0.6,则汪老师预测第二题正确的概率为 .?
14.(2019河南高三月考)将一颗质地均匀的骰子(一种各个面上分别标有1,2,3,4,5,6个点的正方体玩具)先后抛掷2次,则出现向上的点数之和为奇数的概率是 .?
15.(2020浙江高三专题练习)一个口袋里装有大小相同的5个小球,其中红色2个,其余3个颜色各不相同.现从中任意取出3个小球,其中恰有2个小球颜色相同的概率是 ;若变量X为取出的3个小球中红球的个数,则X的数学期望E(X)= .?
16.已知随机变量ξ~B(36,p),且E(ξ)=12,则D(4ξ+3)= .?
四、解答题(本题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤)
17.(10分)(2019上海金山中学高二月考)(1)若ax?x29的二项展开式中x3的系数为94,求实数a的值;
(2)若(3x-1)7=a7x7+a6x6+…+a1x+a0,求a1+a3+a5+a7.
18.(12分)(2020辽宁高三期末)足球是世界普及率最高的运动,我国大力发展校园足球.为了解本地区足球特色学校的发展状况,社会调查小组得到如下统计数据:
年份x
2014
2015
2016
2017
2018
足球特色学校y/百个
0.30
0.60
1.00
1.40
1.70
(1)根据上表数据,计算y与x的相关系数r,并说明y与x的线性相关性强弱;
(已知:0.75≤|r|≤1,则认为y与x线性相关性很强;0.3≤|r|<0.75,则认为y与x线性相关性一般;|r|≤0.25,则认为y与x线性相关性较弱)
(2)求y关于x的线性回归方程,并预测该地区2020年足球特色学校的个数(精确到个).
参考公式和数据:r=∑i=1n(xi-x)(yi-y)∑i=1n(xi-x)2∑i=1n(yi-y)2,∑i=15(xi-x)2=10,∑i=15(yi-y)2=1.3,13≈3.605 6,b^=∑i=1n(xi-x)(yi-y)∑i=1n(xi-x)2,a^=y?b^x.
19.(12分)(2019天津高考)设甲、乙两位同学上学期间,每天7:30之前到校的概率均为23.假定甲、乙两位同学到校情况互不影响,且任一同学每天到校情况相互独立.
(1)用X表示甲同学上学期间的三天中7:30之前到校的天数,求随机变量X的分布列和数学期望;
(2)设M为事件“上学期间的三天中,甲同学在7:30之前到校的天数比乙同学在7:30之前到校的天数恰好多2”,求事件M发生的概率.
20.(12分)(2020山东高三期末)读书可以使人保持思想活力,让人得到智慧启发,让人滋养浩然正气.书籍是文化的重要载体,读书是承继文化的重要方式.某地区为了解学生课余时间的读书情况,随机抽取了n名学生进行调查,根据调查得到的学生日均课余读书时间绘制成如图所示的频率分布直方图,将日均课余读书时间不低于40分钟的学生称为“读书之星”,日均课余读书时间低于40分钟的学生称为“非读书之星”.已知抽取的样本中日均课余读书时间低于10分钟的有10人.
(1)求n,p的值;
(2)根据已知条件完成下面的2×2列联表,并判断是否有95%以上的把握认为“读书之星”与性别有关?
非读书之星
读书之星
总计
男
女
10
55
总计
(3)将上述调查所得到的频率视为概率,现从该地区大量学生中,随机抽取3名学生,每次抽取1名,已知每个人是否被抽到互不影响,记被抽取的“读书之星”人数为随机变量X,求X的分布列和期望.
附:χ2=n(ad-bc)2(a+b)(c+d)(a+c)(b+d),其中n=a+b+c+d.
P(χ2≥k)
0.10
0.05
0.025
0.010
0.005
0.001
k
2.706
3.841
5.024
6.635
7.879
10.828
21.(12分)(2019天津高三月考)某校为了普及环保知识,增强学生的环保意识,在全校组织了一次有关环保知识的竞赛.经过初赛、复赛,甲、乙两个代表队(每队3人)进入了决赛,规定每人回答一个问题,答对为本队赢得10分,答错得0分.假设甲队中每人答对的概率均为34,乙队中3人答对的概率分别为45,34,23,且各人回答正确与否相互之间没有影响,用ξ表示乙队的总得分.
(1)求ξ的分布列及数学期望;
(2)求甲、乙两队总得分之和等于30分且甲队获胜的概率.
22.(12分)(2019青海高三月考)某企业打算处理一批产品,这些产品每箱100件,以箱为单位销售.已知这批产品中每箱出现的废品率只有10%或者20%两种可能,两种可能对应的概率均为0.5.假设该产品正品每件市场价格为100元,废品不值钱.现处理价格为每箱8 400元,遇到废品不予更换.以一箱产品中正品的价格期望值作为决策依据.
(1)在不开箱检验的情况下,判断是否可以购买;
(2)现允许开箱,有放回地随机从一箱中抽取2件产品进行检验.
①若此箱出现的废品率为20%,记抽到的废品数为X,求X的分布列和数学期望;
②若已发现在抽取检验的2件产品中,其中恰有一件是废品,判断是否可以购买.
1228090011595100模块综合测评
(时间:120分钟 满分:150分)
一、单项选择题(本题共8小题,每小题5分,共40分.)
1.(2019甘肃兰州第二十七中学高一期末)如图所示,4个散点图中,不适合用线性回归模型拟合其中两个变量的是( )
解析根据题意,适合用线性回归拟合其中两个变量的散点图必须散点分布比较集中,且大体接近某一条直线,分析选项可得A选项的散点图杂乱无章,最不符合条件.故选A.
答案A
2.(2019云南泸西第一中学高二期中)若An2=3Cn-12,则n的值为( )
A.4 B.5 C.6 D.7
解析因为An2=3Cn-12,所以n(n-1)=3(n-1)(n-2)2,解得n=6或n=1(舍去).故选C.
答案C
3.甲、乙二人争夺一场围棋比赛的冠军,若比赛为“三局两胜”制,甲在每局比赛中获胜的概率均为34,且各局比赛结果相互独立.则在甲获得冠军的情况下,比赛进行了三局的概率为( )
A.13 B.25 C.23 D.45
解析记事件A:甲获得冠军,事件B:比赛进行三局,
事件AB:甲获得冠军,且比赛进行了三局,则第三局甲胜,前两局甲胜了一局,
由独立事件的概率乘法公式得P(AB)=C21×34×14×34=932,
对于事件A,甲获得冠军,包含两种情况:前两局甲胜和事件AB,
所以P(A)=342+932=2732,
所以P(B|A)=P(AB)P(A)=932×3227=13,故选A.
答案A
4.(2020浙江高三专题练习)已知离散型随机变量X的分布列如下,则常数c为( )
X
0
1
P
9c2-c
3-8c
A.13 B.23 C.13或23 D.14
解析由随机变量的分布列知,9c2-c≥0,3-8c≥0,9c2-c+3-8c=1,
所以c=13,故选A.
答案A
5.(2019天津高三期中)两个实习生每人加工一个零件.加工为一等品的概率分别为56和34,两个零件是否加工为一等品相互独立,则这两个零件中恰有一个一等品的概率为( )
A.12 B.13 C.512 D.16
解析记两个零件中恰好有一个一等品的事件为A,即仅第一个实习生加工一等品为事件A1,仅第二个实习生加工一等品为事件A2两种情况,则P(A)=P(A1)+P(A2)=56×14+16×34=13.故选B.
答案B
6.(2019重庆高二期末)若随机变量X~B(n,p),其均值是80,标准差是4,则n和p的值分别是( )
A.100,0.2 B.200,0.4
C.100,0.8 D.200,0.6
解析∵随机变量X~B(n,p),其均值是80,标准差是4,∴由np=80,np(1-p)=16,∴p=0.8,n=100.故选C.
答案C
7.已知随机变量X服从正态分布N(100,4),若P(m
A.100 B.101 C.102 D.103
解析由题意,知P(μ-σ≤X≤μ+σ)=0.683,P(μ-2σ≤X≤μ+2σ)=0.954,
则P(μ-2σ≤X≤μ+2σ)-P(μ-σ≤X≤μ+σ)2=0.954-0.6832=0.135 5,
所以要使得P(m
8.(2020江西高安中学高二期末)某校在“数学联赛”考试后选取了6名教师参加阅卷,试卷共4道解答题,要求将这6名教师分成4组,每组改一道解答题,其中2组各有2名教师,另外2组各有1名教师,则不同的分配方案的种数是( )
A.216 B.420 C.720 D.1 080
解析6人分成4组共有C62C422种不同的分组方案,所以共有C62C422A44=15×62×24=1 080种不同的分配方案.
答案D
二、多项选择题(本题共4小题,每小题5分,共20分)
9.(2019山东高三月考)x+124x8展开式中系数最大的项可以为( )
A.第2项 B.第3项
C.第4项 D.第5项
解析x+124x8的展开式的通项公式为Tk+1=C8k·(x)8-k·124xk=12k·C8k·x4-34k,
其展开式的各项系数依次为1,4,7,7,358,74,716,116,1256,
所以,展开式中系数最大的项是第3项和第4项.
故选BC.
答案BC
10.若随机变量ξ的分布列如下表所示,其中m∈(0,1),则下列结果中正确的是( )
ξ
0
1
P
m
n
A.E(ξ)=m B.D(ξ)=n2
C.E(ξ)=1-m D.D(ξ)=m-m2
解析由离散型随机变量的概率关系可知:n=1-m.
则E(ξ)=0×m+1×n=n=1-m;
D(ξ)=[0-(1-m)]2m+[1-(1-m)]2(1-m)=m-m2=n-n2.
答案CD
11.(2019河北高二期中)下面四个选项中,正确的是( )
A.设a,b,c分别表示数据15,17,14,10,15,17,17,16,14,12的平均数、中位数、众数,则a
C.绘制频率分布直方图时,各小长方形的面积等于相应各组的组距
D.线性回归直线不一定过样本中心点(x,y)
解析对于A,根据数据可求得平均数为a=15+17+14+10+15+17+17+16+14+1210=14710=14.7,从小到大排列可得10,12,14,14,15,15,16,17,17,17,所以中位数为b=15,由数据可知众数为c=17,即a
对于C,绘制频率分布直方图时,各小长方形的面积等于相应各组的频率,所以C错误;
对于D,根据线性回归方程中a^的求法,可知必过样本中心点(x,y),所以D错误.
故选AB.
答案AB
12.一袋中有大小相同的4个红球和2个白球,给出下列结论:
①从中任取3球,恰有一个白球的概率是35;
②从中有放回的取球6次,每次任取一球,则取到红球次数的方差为43;
③现从中不放回的取球2次,每次任取1球,则在第一次取到红球的条件下,第二次再次取到红球的概率为25;
④从中有放回的取球3次,每次任取一球,则至少有一次取到红球的概率为2627.
其中正确的选项是( )
A.① B.② C.③ D.④
解析①从中任取3个球,恰有一个白球的概率是C21C42C63=35,故A正确;
②从中有放回地取球6次,每次任取一球,取到红球次数X~B6,23,其方差为6×23×1-23=43,故B正确;
③从中不放回地取球2次,每次任取一球,则在第一次取到红球后,此时袋中还有3个红球和2个白球,则第二次再次取到红球的概率为35,故C错误;
④从中有放回地取球3次,每次任取一球,每次取到红球的概率为P=23,所以至少有一次取到红球的概率为1-1-233=2627,故D正确.故选ABD.
答案ABD
三、填空题(本题共4小题,每小题5分,共20分)
13.(2019上海大同中学高三月考)某中学的汪老师在教室进行第二轮复习时布置了两道填空题,他预测学生做对第一题的概率为0.8,两题全对的概率为0.6,则汪老师预测第二题正确的概率为 .?
解析设“做对第一道题”为事件A,“做对第二道题”为事件B,
则P(AB)=P(A)P(B)=0.8·P(B)=0.6,
所以P(B)=0.75.
答案0.75
14.(2019河南高三月考)将一颗质地均匀的骰子(一种各个面上分别标有1,2,3,4,5,6个点的正方体玩具)先后抛掷2次,则出现向上的点数之和为奇数的概率是 .?
解析骰子先后投掷2次,所有可能的结果种数共有C61C61=36种.
∵奇数与偶数之和为奇数,
∴向上的点数之和为奇数的结果种数有2C31C31=18种,∴向上的点数之和为奇数的概率P=1836=12.
答案12
15.(2020浙江高三专题练习)一个口袋里装有大小相同的5个小球,其中红色2个,其余3个颜色各不相同.现从中任意取出3个小球,其中恰有2个小球颜色相同的概率是 ;若变量X为取出的3个小球中红球的个数,则X的数学期望E(X)= .?
解析一个口袋里装有大小相同的5个小球,其中红色2个,其余3个颜色各不相同.
现从中任意取出3个小球,
基本事件总数n=C53=10,
其中恰有2个小球颜色相同包含的基本事件个数m=C22C31=3,所以其中恰有2个小球颜色相同的概率是P=mn=310.
变量X为取出的3个小球中红球的个数,则X的可能取值为0,1,2,
P(X=0)=C33C53=110,
P(X=1)=C21C32C53=610=35,
P(X=2)=C22C31C53=310,
数学期望E(X)=0×110+1×610+2×310=65.
答案310 65
16.已知随机变量ξ~B(36,p),且E(ξ)=12,则D(4ξ+3)= .?
解析随机变量ξ~B(36,p),且E(ξ)=12,
所以n=36,且np=36p=12,解得p=13,
所以D(ξ)=np(1-p)=36×13×23=8,
所以D(4ξ+3)=42D(ξ)=16×8=128.
答案128
四、解答题(本题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤)
17.(10分)(2019上海金山中学高二月考)(1)若ax?x29的二项展开式中x3的系数为94,求实数a的值;
(2)若(3x-1)7=a7x7+a6x6+…+a1x+a0,求a1+a3+a5+a7.
解(1)ax?x29的二项展开式通项为Tk+1=C9kax9-k-x2k=-12ka9-kC9kx3k-182,
当3k-182=3,即k=8时,T9=-128aC98x3=9a16x3.
又x3的系数为94,∴9a16=94,解得a=4.
(2)令x=1,得a7+a6+a5+a4+a3+a2+a1+a0=27,①
令x=-1,得-a7+a6-a5+a4-a3+a2-a1+a0=-47,②
①-②,得2a7+2a5+2a3+2a1=27+47=16 512,
∴a1+a3+a5+a7=8 256.
18.(12分)(2020辽宁高三期末)足球是世界普及率最高的运动,我国大力发展校园足球.为了解本地区足球特色学校的发展状况,社会调查小组得到如下统计数据:
年份x
2014
2015
2016
2017
2018
足球特色学校y/百个
0.30
0.60
1.00
1.40
1.70
(1)根据上表数据,计算y与x的相关系数r,并说明y与x的线性相关性强弱;
(已知:0.75≤|r|≤1,则认为y与x线性相关性很强;0.3≤|r|<0.75,则认为y与x线性相关性一般;|r|≤0.25,则认为y与x线性相关性较弱)
(2)求y关于x的线性回归方程,并预测该地区2020年足球特色学校的个数(精确到个).
参考公式和数据:r=∑i=1n(xi-x)(yi-y)∑i=1n(xi-x)2∑i=1n(yi-y)2,∑i=15(xi-x)2=10,∑i=15(yi-y)2=1.3,13≈3.605 6,b^=∑i=1n(xi-x)(yi-y)∑i=1n(xi-x)2,a^=y?b^x.
解(1)由题得x=2 016,y=1,所以r=∑i=15(xi-x)(yi-y)∑i=15(xi-x)2∑i=15(yi-y)2=3.610×1.3
=3.63.605 6≈0.998>0.7,
故y与x线性相关性很强.
(2)b^=∑i=15(xi-x)(yi-y)∑i=15(xi-x)2=
(-2)×(-0.7)+(-1)×(-0.4)+1×0.4+2×0.74+1+0+1+4
=0.36,
a^=y?b^x=1-2 016×0.36=-724.76,
∴y关于x的线性回归方程是y^=0.36x-724.76.
当x=2 020时,y^=0.36x-724.76=2.44,
即该地区2020年足球特色学校有244个.
19.(12分)(2019天津高考)设甲、乙两位同学上学期间,每天7:30之前到校的概率均为23.假定甲、乙两位同学到校情况互不影响,且任一同学每天到校情况相互独立.
(1)用X表示甲同学上学期间的三天中7:30之前到校的天数,求随机变量X的分布列和数学期望;
(2)设M为事件“上学期间的三天中,甲同学在7:30之前到校的天数比乙同学在7:30之前到校的天数恰好多2”,求事件M发生的概率.
解(1)因为甲同学上学期间的三天中到校情况相互独立,且每天7:30之前到校的概率均为23,故X~B3,23,从而P(X=k)=C3k23k133-k,k=0,1,2,3.
所以,随机变量X的分布列为
X
0
1
2
3
P
127
29
49
827
随机变量X的数学期望E(X)=3×23=2.
(2)设乙同学上学期间的三天中7:30之前到校的天数为Y,则Y~B3,23,且M={X=3,Y=1}∪{X=2,Y=0}.由题意知事件{X=3,Y=1}与{X=2,Y=0}互斥,且事件{X=3}与{Y=1},事件{X=2}与{Y=0}均相互独立,从而由(1)知P(M)=P({X=3,Y=1}∪{X=2,Y=0})=P(X=3,Y=1)+P(X=2,Y=0)=P(X=3)P(Y=1)+P(X=2)P(Y=0)=827×29+49×127=20243.
20.(12分)(2020山东高三期末)读书可以使人保持思想活力,让人得到智慧启发,让人滋养浩然正气.书籍是文化的重要载体,读书是承继文化的重要方式.某地区为了解学生课余时间的读书情况,随机抽取了n名学生进行调查,根据调查得到的学生日均课余读书时间绘制成如图所示的频率分布直方图,将日均课余读书时间不低于40分钟的学生称为“读书之星”,日均课余读书时间低于40分钟的学生称为“非读书之星”.已知抽取的样本中日均课余读书时间低于10分钟的有10人.
(1)求n,p的值;
(2)根据已知条件完成下面的2×2列联表,并判断是否有95%以上的把握认为“读书之星”与性别有关?
非读书之星
读书之星
总计
男
女
10
55
总计
(3)将上述调查所得到的频率视为概率,现从该地区大量学生中,随机抽取3名学生,每次抽取1名,已知每个人是否被抽到互不影响,记被抽取的“读书之星”人数为随机变量X,求X的分布列和期望.
附:χ2=n(ad-bc)2(a+b)(c+d)(a+c)(b+d),其中n=a+b+c+d.
P(χ2≥k)
0.10
0.05
0.025
0.010
0.005
0.001
k
2.706
3.841
5.024
6.635
7.879
10.828
解(1)(0.005+p+0.018+0.020+0.022+0.025)×10=1,解得p=0.01,所以n=100.1=100.
(2)因为n=100,所以“读书之星”有100×0.25=25.从而2×2列联表如下表所示
非读书之星
读书之星
总计
男
30
15
45
女
45
10
55
总计
75
25
100
将2×2列联表中的数据代入公式计算得
χ2=100×(30×10-15×45)245×55×75×25=10033≈3.030,
因为3.030<3.841,所以没有95%以上的把握认为“读书之星”与性别有关.
(3)将频率视为概率,即从该地区学生中抽取一名学生是“读书之星”的概率为14.
由题意可知X~B3,14,
所以P(X=0)=C30×140×1-143=2764,
P(X=1)=C31×14×1-142=2764,
P(X=2)=C32×142×1-14=964,
P(X=3)=C33×143=164,
所以X的分布列为
X
0
1
2
3
P
2764
2764
964
164
故E(X)=3×14=34.
21.(12分)(2019天津高三月考)某校为了普及环保知识,增强学生的环保意识,在全校组织了一次有关环保知识的竞赛.经过初赛、复赛,甲、乙两个代表队(每队3人)进入了决赛,规定每人回答一个问题,答对为本队赢得10分,答错得0分.假设甲队中每人答对的概率均为34,乙队中3人答对的概率分别为45,34,23,且各人回答正确与否相互之间没有影响,用ξ表示乙队的总得分.
(1)求ξ的分布列及数学期望;
(2)求甲、乙两队总得分之和等于30分且甲队获胜的概率.
解(1)由题意知,ξ的所有可能取值为0,10,20,30.
P(ξ=0)=15×14×13=160;
P(ξ=10)=45×14×13+15×34×13+15×14×23=960=320;
P(ξ=20)=45×34×13+45×14×23+15×34×23=2660=1330;
P(ξ=30)=45×34×23=2460=25.
∴ξ的分布列为
ξ
0
10
20
30
P
160
320
1330
25
∴E(ξ)=0×160+10×320+20×1330+30×25=1336.
(2)用A表示“甲得30分乙得0分”,用B表示“甲得20分乙得10分”,且A,B互斥,
又P(A)=343×160=91 280,P(B)=C32342×14×320=811 280,甲、乙两队得分总和为30分且甲获胜的概率为P(A+B)=P(A)+P(B)=901 280=9128.
22.(12分)(2019青海高三月考)某企业打算处理一批产品,这些产品每箱100件,以箱为单位销售.已知这批产品中每箱出现的废品率只有10%或者20%两种可能,两种可能对应的概率均为0.5.假设该产品正品每件市场价格为100元,废品不值钱.现处理价格为每箱8 400元,遇到废品不予更换.以一箱产品中正品的价格期望值作为决策依据.
(1)在不开箱检验的情况下,判断是否可以购买;
(2)现允许开箱,有放回地随机从一箱中抽取2件产品进行检验.
①若此箱出现的废品率为20%,记抽到的废品数为X,求X的分布列和数学期望;
②若已发现在抽取检验的2件产品中,其中恰有一件是废品,判断是否可以购买.
解(1)在不开箱检验的情况下,一箱产品中正品的价格期望值为E(ξ)=100×(1-0.2)×100×0.5+100×(1-0.1)×100×0.5=8 500>8 400,
∴在不开箱检验的情况下,可以购买.
(2)①X的可能取值为0,1,2,
P(X=0)=C20×0.20×0.82=0.64,
P(X=1)=C21×0.21×0.81=0.32,
P(X=2)=C22×0.22×0.80=0.04,
∴X的分布列为
X
0
1
2
P
0.64
0.32
0.04
E(X)=0×0.64+1×0.32+2×0.04=0.4.
②设事件A:发现在抽取检验的2件产品中,其中恰有一件是废品,
则P(A)=C21×0.2×0.8×0.5+C21×0.1×0.9×0.5=0.25,一箱产品中,设正品的价格的期望值为η,则η=8 000,9 000,
事件B1:抽取的废品率为20%的一箱,
则P(η=8 000)=P(B1|A)=P(AB1)P(A)=C21×0.2×0.8×0.50.25=0.64,
事件B2:抽取的废品率为10%的一箱,
则P(η=9 000)=P(B2|A)=P(AB2)P(A)=C21×0.1×0.9×0.50.25=0.36,∴E(η)=8 000×0.64+9 000×0.36=8 360<8 400,∴已发现在抽取检验的2件产品中,其中恰有一件是废品,则不可以购买.
