2.2.2函数的表示法(第二课时)课件(共48张PPT)-2021-2022学年高一上学期数学北师大版(2019)必修第一册
文档属性
| 名称 | 2.2.2函数的表示法(第二课时)课件(共48张PPT)-2021-2022学年高一上学期数学北师大版(2019)必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-30 00:00:00 | ||
图片预览








文档简介
2.2.2函数的表示法
第二课时
教学目标
01
02
倒数型结构函数图像画法
一次分式型函数图像画法
03
含一个绝对值一次和二 次函数图像画法
含绝对值函数图像画法
重点
难点
对图像的渐近线与图像翻转变换的理解
环节一
分式函数简介
在我们的学习中常见到复杂的分式结构的函数式, 通常采取“分离” 的方法转化成两种主要类型:(1)一次分式型
f ( x) =????????+????????????+????????????≠????????;(2)倒数结构型 f (x)=????????+????????.
下面画出两种类型函数的示意图,以便从中看出函数的性质
?
分式函数结构形态
f ( x) =????????+????????????+????=????????+????????+????????
其图像的渐近线是????=?????????,????=????????,(观察得, ????=?????????来自于分式的分母为零时,????=????????,来自上下x的系数之比)两条渐近线互相垂直,交点处是对称中心(?????????,????????)
?
一次分式类型
环节二
一次分式函数图像
f ( x) =????????+????????????+????=????????+????????+????????
先在直角坐标系中画两条渐近线(画成虚线),构成参考坐标系,然后,在竖渐近线前后取一些点,描出图像(双曲线,跟反比例图像一样)
?
一次分式画法
01
描点法
实战
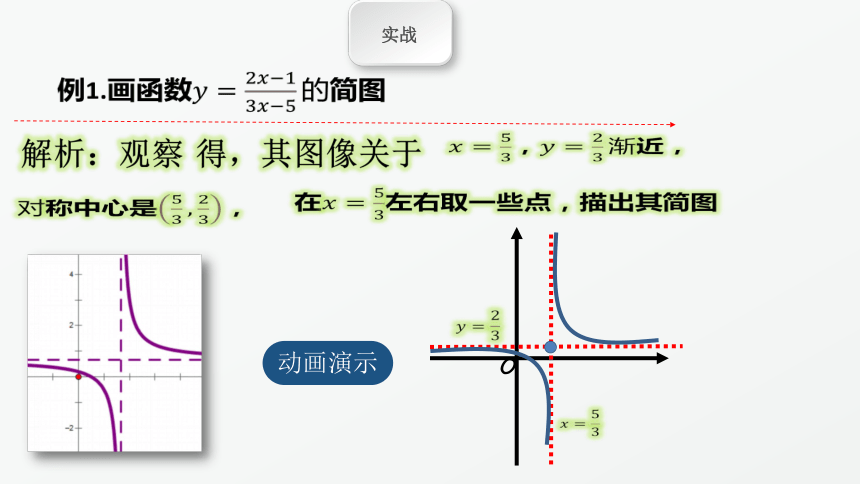
例1.画函数????=?????????
实战
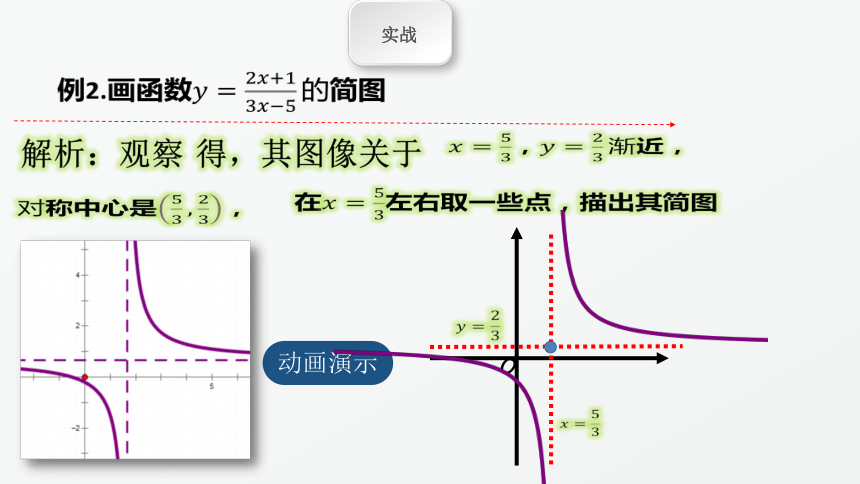
例2.画函数????=????????+????????????
实战
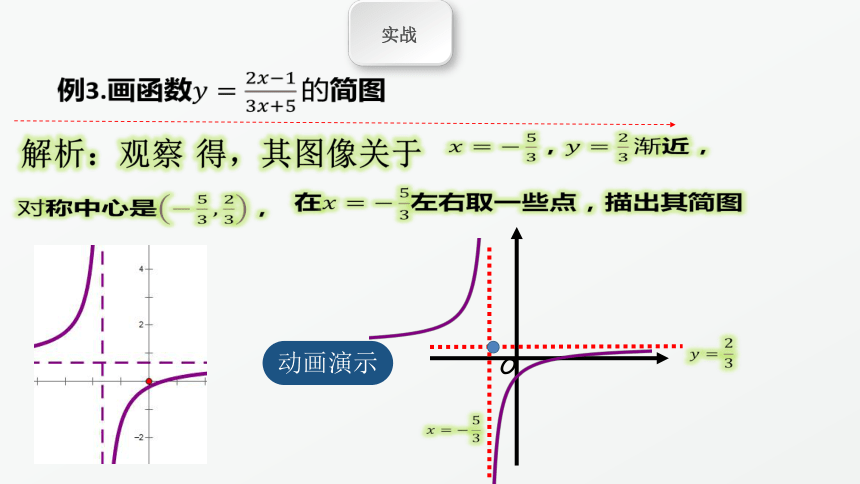
例3.画函数????=?????????????????????+????的简图
?
解析:观察 得,其图像关于
????=?????????,????=????????渐近,
?
对称中心是?????????,????????,
?
在????=?????????左右取一些点,描出其简图
?
动画演示
O
????=?????????
?
????=????????
?
实战
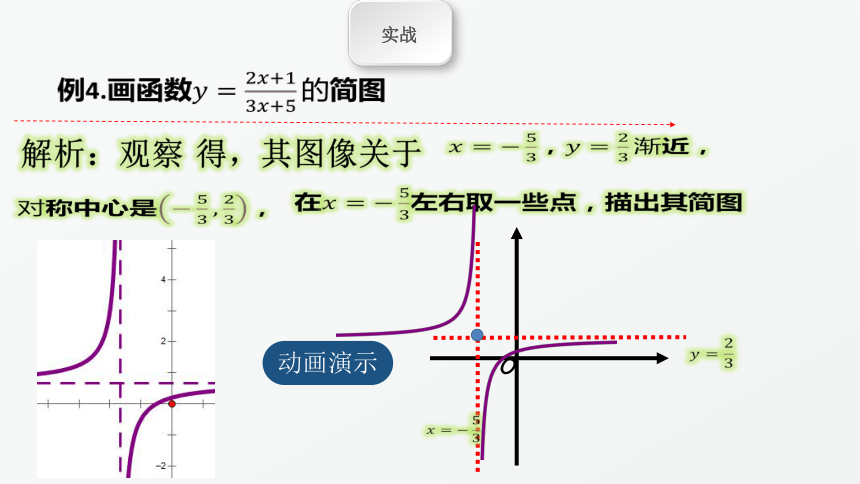
例4.画函数????=????????+????????????+????的简图
?
解析:观察 得,其图像关于
????=?????????,????=????????渐近,
?
对称中心是?????????,????????,
?
在????=?????????左右取一些点,描出其简图
?
动画演示
O
????=?????????
?
????=????????
?
f ( x) =????????+????????????+????=????????+????????+????????
先在直角坐标系中画两条渐近线(画成虚线),构成参考坐标系,然后,画反比例函数????=????????的图像,根据????????的符号左右平移,根据????????的符号上下平移,得到最终图像。
?
一次分式画法
02
平移法
实战
例5.画函数????=?????????
实战
例5.画函数????=?????????
实战
例5.画函数????=?????????
实战
例6.画函数????=????????+????????????
实战
例6.画函数????=????????+????????????
实战
例6.画函数????=????????+????????????
实战
例6.画函数????=????????+????????????
实战
例7.画函数????=?????????????????????+????的简图
?
解析:观察 得,其图像关于
????=?????????,????=????????渐近,
?
对称中心是?????????,????????,
?
将????=?????????????????向左平移????????个单位,
?
O
????=?????????
?
????=????????
?
实战
例7.画函数????=?????????????????????+????的简图
?
解析:观察 得,其图像关于
????=?????????,????=????????渐近,
?
对称中心是?????????,????????,
?
将????=?????????????????向左平移????????个单位,
?
O
????=?????????
?
????=????????
?
向上平移????????个单位,
?
实战
例7.画函数????=?????????????????????+????的简图
?
解析:观察 得,其图像关于
????=?????????,????=????????渐近,
?
对称中心是?????????,????????,
?
将????=?????????????????向左平移????????个单位,
?
O
????=?????????
?
????=????????
?
向上平移????????个单位,
?
实战
例8.画函数????=????????+????????????+????的简图
?
解析:观察 得,其图像关于
????=?????????,????=????????渐近,
?
对称中心是?????????,????????,
?
O
????=?????????
?
????=????????
?
将????=?????????????的图像向左平移????????个单位,
?
实战
例8.画函数????=????????+????????????+????的简图
?
解析:观察 得,其图像关于
????=?????????,????=????????渐近,
?
对称中心是?????????,????????,
?
O
????=?????????
?
????=????????
?
将????=?????????????的图像向左平移????????个单位,
?
实战
例8.画函数????=????????+????????????+????的简图
?
解析:观察 得,其图像关于
????=?????????,????=????????渐近,
?
对称中心是?????????,????????,
?
O
????=?????????
?
????=????????
?
将????=?????????????的图像向左平移????????个单位,
?
向上平移????????个单位,
?
环节三
倒数结构型函数图像
倒数结构函数图像
形如????=????????+????????,
例9.画????=????+????????的图像
?
01
画渐近线????=????
?
O
02
画关键点
?
1
-1
03
画对勾
?
倒数结构函数图像
形如????=????????+????????,
例10.画????=??????????????的图像
?
01
画渐近线????=?????
?
O
02
画关键点
?
1
-1
03
画对勾
?
倒数结构函数图像
形如????=????????+????????,
例11.画????=?????????????的图像
?
01
画渐近线????=????
?
O
02
画关键点
?
1
-1
03
画飘带
?
倒数结构函数图像
形如????=????????+????????,
例12.画????=?????+????????的图像
?
01
画渐近线????=?????
?
O
02
画关键点
?
1
-1
03
画飘带
?
环节四
含一个绝对值的一次函数图像
????=????????+????+????????
例13.
画(????)????=?????+
例13.
画(2)????=
环节五
含一个绝对值的二次函数图像
类型一????????=????????????+????????+?????
例14.????=?????????
类型二???????=????????????+????????+????
例15.画????=????
类型三???????=????????????+????????+????
例16.画????=?????????????????
课堂小结
1.核心要点
一次分式函数图像画法
2.数学素养
体会化归与转化思想的应用
提高作图能力。
倒数结构函数图像画法
含一个绝对值一次函数图像画法
含一个绝对值二次函数图像画法
谢谢观看
第二课时
教学目标
01
02
倒数型结构函数图像画法
一次分式型函数图像画法
03
含一个绝对值一次和二 次函数图像画法
含绝对值函数图像画法
重点
难点
对图像的渐近线与图像翻转变换的理解
环节一
分式函数简介
在我们的学习中常见到复杂的分式结构的函数式, 通常采取“分离” 的方法转化成两种主要类型:(1)一次分式型
f ( x) =????????+????????????+????????????≠????????;(2)倒数结构型 f (x)=????????+????????.
下面画出两种类型函数的示意图,以便从中看出函数的性质
?
分式函数结构形态
f ( x) =????????+????????????+????=????????+????????+????????
其图像的渐近线是????=?????????,????=????????,(观察得, ????=?????????来自于分式的分母为零时,????=????????,来自上下x的系数之比)两条渐近线互相垂直,交点处是对称中心(?????????,????????)
?
一次分式类型
环节二
一次分式函数图像
f ( x) =????????+????????????+????=????????+????????+????????
先在直角坐标系中画两条渐近线(画成虚线),构成参考坐标系,然后,在竖渐近线前后取一些点,描出图像(双曲线,跟反比例图像一样)
?
一次分式画法
01
描点法
实战
例1.画函数????=?????????
实战
例2.画函数????=????????+????????????
实战
例3.画函数????=?????????????????????+????的简图
?
解析:观察 得,其图像关于
????=?????????,????=????????渐近,
?
对称中心是?????????,????????,
?
在????=?????????左右取一些点,描出其简图
?
动画演示
O
????=?????????
?
????=????????
?
实战
例4.画函数????=????????+????????????+????的简图
?
解析:观察 得,其图像关于
????=?????????,????=????????渐近,
?
对称中心是?????????,????????,
?
在????=?????????左右取一些点,描出其简图
?
动画演示
O
????=?????????
?
????=????????
?
f ( x) =????????+????????????+????=????????+????????+????????
先在直角坐标系中画两条渐近线(画成虚线),构成参考坐标系,然后,画反比例函数????=????????的图像,根据????????的符号左右平移,根据????????的符号上下平移,得到最终图像。
?
一次分式画法
02
平移法
实战
例5.画函数????=?????????
实战
例5.画函数????=?????????
实战
例5.画函数????=?????????
实战
例6.画函数????=????????+????????????
实战
例6.画函数????=????????+????????????
实战
例6.画函数????=????????+????????????
实战
例6.画函数????=????????+????????????
实战
例7.画函数????=?????????????????????+????的简图
?
解析:观察 得,其图像关于
????=?????????,????=????????渐近,
?
对称中心是?????????,????????,
?
将????=?????????????????向左平移????????个单位,
?
O
????=?????????
?
????=????????
?
实战
例7.画函数????=?????????????????????+????的简图
?
解析:观察 得,其图像关于
????=?????????,????=????????渐近,
?
对称中心是?????????,????????,
?
将????=?????????????????向左平移????????个单位,
?
O
????=?????????
?
????=????????
?
向上平移????????个单位,
?
实战
例7.画函数????=?????????????????????+????的简图
?
解析:观察 得,其图像关于
????=?????????,????=????????渐近,
?
对称中心是?????????,????????,
?
将????=?????????????????向左平移????????个单位,
?
O
????=?????????
?
????=????????
?
向上平移????????个单位,
?
实战
例8.画函数????=????????+????????????+????的简图
?
解析:观察 得,其图像关于
????=?????????,????=????????渐近,
?
对称中心是?????????,????????,
?
O
????=?????????
?
????=????????
?
将????=?????????????的图像向左平移????????个单位,
?
实战
例8.画函数????=????????+????????????+????的简图
?
解析:观察 得,其图像关于
????=?????????,????=????????渐近,
?
对称中心是?????????,????????,
?
O
????=?????????
?
????=????????
?
将????=?????????????的图像向左平移????????个单位,
?
实战
例8.画函数????=????????+????????????+????的简图
?
解析:观察 得,其图像关于
????=?????????,????=????????渐近,
?
对称中心是?????????,????????,
?
O
????=?????????
?
????=????????
?
将????=?????????????的图像向左平移????????个单位,
?
向上平移????????个单位,
?
环节三
倒数结构型函数图像
倒数结构函数图像
形如????=????????+????????,
例9.画????=????+????????的图像
?
01
画渐近线????=????
?
O
02
画关键点
?
1
-1
03
画对勾
?
倒数结构函数图像
形如????=????????+????????,
例10.画????=??????????????的图像
?
01
画渐近线????=?????
?
O
02
画关键点
?
1
-1
03
画对勾
?
倒数结构函数图像
形如????=????????+????????,
例11.画????=?????????????的图像
?
01
画渐近线????=????
?
O
02
画关键点
?
1
-1
03
画飘带
?
倒数结构函数图像
形如????=????????+????????,
例12.画????=?????+????????的图像
?
01
画渐近线????=?????
?
O
02
画关键点
?
1
-1
03
画飘带
?
环节四
含一个绝对值的一次函数图像
????=????????+????+????????
例13.
画(????)????=?????+
例13.
画(2)????=
环节五
含一个绝对值的二次函数图像
类型一????????=????????????+????????+?????
例14.????=?????????
类型二???????=????????????+????????+????
例15.画????=????
类型三???????=????????????+????????+????
例16.画????=?????????????????
课堂小结
1.核心要点
一次分式函数图像画法
2.数学素养
体会化归与转化思想的应用
提高作图能力。
倒数结构函数图像画法
含一个绝对值一次函数图像画法
含一个绝对值二次函数图像画法
谢谢观看
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
