13.2.2 空间两条直线位置关系(1)同步练习-2020-2021学年高一下学期数学苏教版(2019)必修第二册(Word版含解析)
文档属性
| 名称 | 13.2.2 空间两条直线位置关系(1)同步练习-2020-2021学年高一下学期数学苏教版(2019)必修第二册(Word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 199.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-30 20:38:32 | ||
图片预览

文档简介
空间两条直线的位置关系(1)
课本温习
1.
若两条直线没有公共点,则这两条直线的位置关系是( )
A.
相交
B.
平行
C.
异面
D.
平行或异面
2.
分别在两个平面内的两条直线间的位置关系是( )
A.
异面
B.
平行
C.
相交
D.
以上都有可能
3.
如果一个角两边与另一个角的两边分别平行,并且方向不相同,那么这两个角( )
A.
相等
B.
互补
C.
相等或互补
D.
无法确定
4.
在正方体ABCDA1B1C1D1中,与AA1平行的棱共有( )
A.
1条
B.
2条
C.
3条
D.
4条
固基强能
5.
如图,将三棱柱ABCA1B1C1作截面EFBA,截去一部分后,剩下几何体EFC1ABC,则∠EFC1与∠ABC的关系是( )
A.
相等
B.
互补
C.
相等或互补
D.
无法确定
6.
如图,在正方体ABCDA1B1C1D1中,E,F,G,H分别为边B1C1,C1C,A1A,AD的中点,则EF与GH的位置关系是( )
A.
平行
B.
相交
C.
异面
D.
无法确定
7.
(多选)若∠ABC和∠PQR的两边分别满足AB∥PQ,BC∥QR,∠ABC=30°,则∠PQR的度数可能为( )
A.
30°
B.
60°
C.
120°
D.
150°
8.
(多选)已知l1,l2,l3是空间三条不同的直线,则下列命题错误的是( )
A.
l1⊥l2,l2⊥l3?l1∥l3
B.
l1⊥l2,l2∥l3?l1⊥l3
C.
l1∥l2∥l3?l1,l2,l3共面
D.
l1,l2,l3共点?l1,l2,l3共面
9.如图所示,木工师傅沿长方体木块ABCD-A1B1C1D1中棱BC和上底面的中心E将长方体木块锯开,问怎样画线?
10.
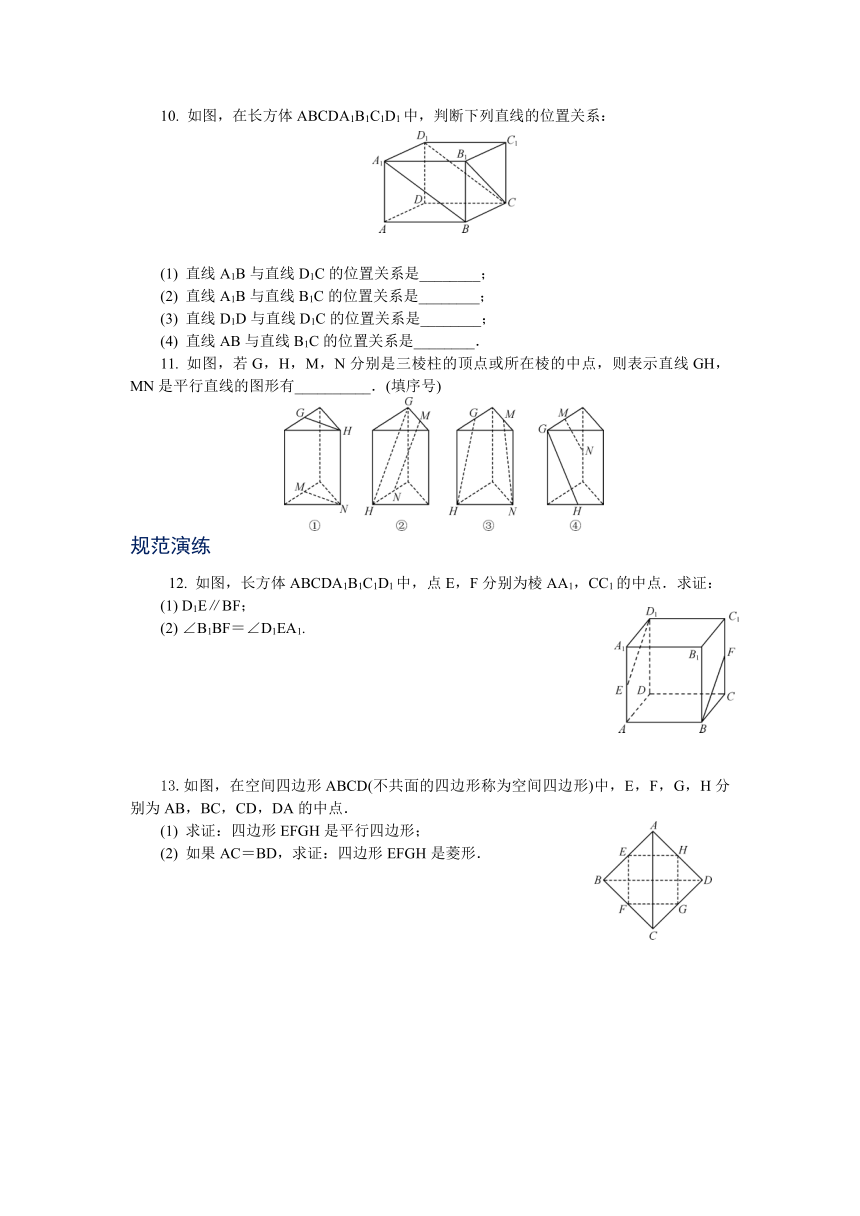
如图,在长方体ABCDA1B1C1D1中,判断下列直线的位置关系:
(1)
直线A1B与直线D1C的位置关系是________;
(2)
直线A1B与直线B1C的位置关系是________;
(3)
直线D1D与直线D1C的位置关系是________;
(4)
直线AB与直线B1C的位置关系是________.
11.
如图,若G,H,M,N分别是三棱柱的顶点或所在棱的中点,则表示直线GH,MN是平行直线的图形有__________.(填序号)
规范演练
12.
如图,长方体ABCDA1B1C1D1中,点E,F分别为棱AA1,CC1的中点.求证:
(1)
D1E∥BF;
(2)
∠B1BF=∠D1EA1.
13.如图,在空间四边形ABCD(不共面的四边形称为空间四边形)中,E,F,G,H分别为AB,BC,CD,DA的中点.
(1)
求证:四边形EFGH是平行四边形;
(2)
如果AC=BD,求证:四边形EFGH是菱形.
空间两条直线的位置关系
1.
D 解析:根据平行直线和异面直线的定义得到,故选D.
2.
D 解析:根据正方体中存在的线线关系判断.故选D.
3.
B 解析:根据等角定理,但条件中方向相同变成了方向不相同,所以两角只能互补.故选B.
4.
C 解析:∵
正方体的每个面是正方形,∴
AA1∥BB1,AA1∥DD1.∵
CC1∥BB1,∴
AA1∥CC1.∴
与AA1平行的棱共有3条.故选C.
5.
A 解析:由题意,EF∥AB,FC1∥BC,所以∠EFC1与∠ABC两边分别平行,且方向相同,所以∠EFC1与∠ABC相等.故选A.
6.
A 解析:如图,连结B1C与A1D,因为E,F分别为B1C1,C1C的中点,所以EF∥B1C.同理可得GH∥A1D.由正方体得A1D∥B1C,所以EF∥GH.故选A.
7.
AD 解析:∵
∠ABC的两边和∠PQR的两边分别平行,且方向相同或相反,∴
∠PQR=30°或150°.故选AD.
8.
ACD 解析:当l1⊥l2,l2⊥l3时,l1与l3也可能相交或异面,故A不正确;当l1∥l2∥l3时,l1,l2,l3未必共面,如三棱柱的三条侧棱,故C不正确;当l1,l2,l3共点时,l1,l2,l3未必共面,如正方体中从同一顶点出发的三条棱,故D不正确.故选ACD.
9.解:在面A1B1C1D1内过点E作B1C1的平行线,与A1B1,C1D1分别相交于F、G,连接BF,CG即可.
10.
(1)
平行 (2)
异面 (3)
相交 (4)
异面
解析:根据探究知道直线D1D与直线D1C相交于点D1,∴
(3)应该填“相交”;直线A1B与直线D1C在平面A1BCD1中,且没有交点,则两直线平行,∴
(1)应该填“平行”;点A1,B,B1在平面A1BB1内,而C不在平面A1BB1内,则直线A1B与直线B1C异面.同理,直线AB与直线B1C异面,∴
(2)(4)应该填“异面”.
11.
① 解析:对于①:因为GM∥HN,且GM=HN,所以四边形GMNH是平行四边形,所以GH∥MN,所以①正确;对于③:GM∥HN且GM≠HN,所以四边形GHNM是梯形,所以HG,NM必相交,所以③错误;对于②④:直线GH与MN既不平行,也不相交,是异面直线,所以②④错误.
12.证明:(1)
如图,取BB1的中点M,连结EM,C1M.
在矩形ABB1A1中,易得EM綊A1B1.
∵
A1B1綊C1D1,∴
EM綊C1D1,
∴
四边形EMC1D1为平行四边形,
∴
D1E∥C1M.
在矩形BCC1B1中,易得MB綊C1F,
∴
BF綊C1M.∴
D1E∥BF.
(2)
∵
ED1∥BF,BM∥EA1,又∠B1BF与∠D1EA1的对应边方向相同,
∴
∠B1BF=∠D1EA1.
13.
证明:(1)
在△ABD中,E,H分别为AB,
AD的中点,∴
EH∥BD且EH=BD.
同理在△BCD中,FG∥BD且FG=BD.
∴
EH∥FG且EH=FG.
∴
四边形EFGH为平行四边形.
(2)
由(1)同理可得EF=HG=AC,
而BD=AC,
∴
EH=HG=GF=FE,
∴
平行四边形EFGH是菱形.
课本温习
1.
若两条直线没有公共点,则这两条直线的位置关系是( )
A.
相交
B.
平行
C.
异面
D.
平行或异面
2.
分别在两个平面内的两条直线间的位置关系是( )
A.
异面
B.
平行
C.
相交
D.
以上都有可能
3.
如果一个角两边与另一个角的两边分别平行,并且方向不相同,那么这两个角( )
A.
相等
B.
互补
C.
相等或互补
D.
无法确定
4.
在正方体ABCDA1B1C1D1中,与AA1平行的棱共有( )
A.
1条
B.
2条
C.
3条
D.
4条
固基强能
5.
如图,将三棱柱ABCA1B1C1作截面EFBA,截去一部分后,剩下几何体EFC1ABC,则∠EFC1与∠ABC的关系是( )
A.
相等
B.
互补
C.
相等或互补
D.
无法确定
6.
如图,在正方体ABCDA1B1C1D1中,E,F,G,H分别为边B1C1,C1C,A1A,AD的中点,则EF与GH的位置关系是( )
A.
平行
B.
相交
C.
异面
D.
无法确定
7.
(多选)若∠ABC和∠PQR的两边分别满足AB∥PQ,BC∥QR,∠ABC=30°,则∠PQR的度数可能为( )
A.
30°
B.
60°
C.
120°
D.
150°
8.
(多选)已知l1,l2,l3是空间三条不同的直线,则下列命题错误的是( )
A.
l1⊥l2,l2⊥l3?l1∥l3
B.
l1⊥l2,l2∥l3?l1⊥l3
C.
l1∥l2∥l3?l1,l2,l3共面
D.
l1,l2,l3共点?l1,l2,l3共面
9.如图所示,木工师傅沿长方体木块ABCD-A1B1C1D1中棱BC和上底面的中心E将长方体木块锯开,问怎样画线?
10.
如图,在长方体ABCDA1B1C1D1中,判断下列直线的位置关系:
(1)
直线A1B与直线D1C的位置关系是________;
(2)
直线A1B与直线B1C的位置关系是________;
(3)
直线D1D与直线D1C的位置关系是________;
(4)
直线AB与直线B1C的位置关系是________.
11.
如图,若G,H,M,N分别是三棱柱的顶点或所在棱的中点,则表示直线GH,MN是平行直线的图形有__________.(填序号)
规范演练
12.
如图,长方体ABCDA1B1C1D1中,点E,F分别为棱AA1,CC1的中点.求证:
(1)
D1E∥BF;
(2)
∠B1BF=∠D1EA1.
13.如图,在空间四边形ABCD(不共面的四边形称为空间四边形)中,E,F,G,H分别为AB,BC,CD,DA的中点.
(1)
求证:四边形EFGH是平行四边形;
(2)
如果AC=BD,求证:四边形EFGH是菱形.
空间两条直线的位置关系
1.
D 解析:根据平行直线和异面直线的定义得到,故选D.
2.
D 解析:根据正方体中存在的线线关系判断.故选D.
3.
B 解析:根据等角定理,但条件中方向相同变成了方向不相同,所以两角只能互补.故选B.
4.
C 解析:∵
正方体的每个面是正方形,∴
AA1∥BB1,AA1∥DD1.∵
CC1∥BB1,∴
AA1∥CC1.∴
与AA1平行的棱共有3条.故选C.
5.
A 解析:由题意,EF∥AB,FC1∥BC,所以∠EFC1与∠ABC两边分别平行,且方向相同,所以∠EFC1与∠ABC相等.故选A.
6.
A 解析:如图,连结B1C与A1D,因为E,F分别为B1C1,C1C的中点,所以EF∥B1C.同理可得GH∥A1D.由正方体得A1D∥B1C,所以EF∥GH.故选A.
7.
AD 解析:∵
∠ABC的两边和∠PQR的两边分别平行,且方向相同或相反,∴
∠PQR=30°或150°.故选AD.
8.
ACD 解析:当l1⊥l2,l2⊥l3时,l1与l3也可能相交或异面,故A不正确;当l1∥l2∥l3时,l1,l2,l3未必共面,如三棱柱的三条侧棱,故C不正确;当l1,l2,l3共点时,l1,l2,l3未必共面,如正方体中从同一顶点出发的三条棱,故D不正确.故选ACD.
9.解:在面A1B1C1D1内过点E作B1C1的平行线,与A1B1,C1D1分别相交于F、G,连接BF,CG即可.
10.
(1)
平行 (2)
异面 (3)
相交 (4)
异面
解析:根据探究知道直线D1D与直线D1C相交于点D1,∴
(3)应该填“相交”;直线A1B与直线D1C在平面A1BCD1中,且没有交点,则两直线平行,∴
(1)应该填“平行”;点A1,B,B1在平面A1BB1内,而C不在平面A1BB1内,则直线A1B与直线B1C异面.同理,直线AB与直线B1C异面,∴
(2)(4)应该填“异面”.
11.
① 解析:对于①:因为GM∥HN,且GM=HN,所以四边形GMNH是平行四边形,所以GH∥MN,所以①正确;对于③:GM∥HN且GM≠HN,所以四边形GHNM是梯形,所以HG,NM必相交,所以③错误;对于②④:直线GH与MN既不平行,也不相交,是异面直线,所以②④错误.
12.证明:(1)
如图,取BB1的中点M,连结EM,C1M.
在矩形ABB1A1中,易得EM綊A1B1.
∵
A1B1綊C1D1,∴
EM綊C1D1,
∴
四边形EMC1D1为平行四边形,
∴
D1E∥C1M.
在矩形BCC1B1中,易得MB綊C1F,
∴
BF綊C1M.∴
D1E∥BF.
(2)
∵
ED1∥BF,BM∥EA1,又∠B1BF与∠D1EA1的对应边方向相同,
∴
∠B1BF=∠D1EA1.
13.
证明:(1)
在△ABD中,E,H分别为AB,
AD的中点,∴
EH∥BD且EH=BD.
同理在△BCD中,FG∥BD且FG=BD.
∴
EH∥FG且EH=FG.
∴
四边形EFGH为平行四边形.
(2)
由(1)同理可得EF=HG=AC,
而BD=AC,
∴
EH=HG=GF=FE,
∴
平行四边形EFGH是菱形.
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
