2020—2021学年沪科版九年级数学上册第23章解直角三角形单元测试题(word解析版)
文档属性
| 名称 | 2020—2021学年沪科版九年级数学上册第23章解直角三角形单元测试题(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 173.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-31 13:10:53 | ||
图片预览



文档简介
第23章 解直角三角形
一、选择题(本大题共7小题,每小题4分,共28分)
1.已知:在Rt△ABC中,∠C=90°,BC=3,AC=4,则tanB的值是
( )
A.
B.
C.
D.
2.如图1,坡角为30°的斜坡上两树间的水平距离AC为2
m,则两树间的坡面距离AB为
( )
图1
A.4
m
B.
m
C.
m
D.4
m
3.当∠A,∠B为锐角,且∠A+∠B=90°时,下列结论错误的是
( )
A.cosA=sinB
B.sinA=cosB
C.sinA=cos(90°-∠A)
D.sin(90°-∠A)=sinA
4.如图2所示,一次函数y=2x+2的图象与x轴交于点A,与y轴交于点B,则下列结论正确的是
( )
图2
A.sin∠BAO=
B.tan∠BAO=
C.tan∠ABO=-
D.cos∠ABO=
5.如图3所示,每个小正方形的边长均为1,A,B,C均为小正方形的顶点,则∠ABC的正弦值为
( )
图3
A.1
B.
C.
D.
6.长为4
m的梯子搭在墙上与地面成45°角,作业时调整成60°角,如图4所示,则梯子的顶端沿墙面升高的距离为
( )
图4
A.(2-)m
B.2(-)m
C.(2-)m
D.2(+)m
7.将一副三角尺如图5①摆放在一起,示意图如图②,连接AD,则∠ADC的正切值为( )
图5
A.-1
B.+1
C.2
D.3
二、填空题(本大题共5小题,每小题5分,共25分)
8.若tan(α+10°)=1,则锐角α的度数是 .?
9.已知α为锐角,当无意义时,sin(α+15°)+cos(α-15°)的值为 .?
10.如果一个等腰三角形的三条边长分别为1,1,,那么这个等腰三角形底角的度数为 .?
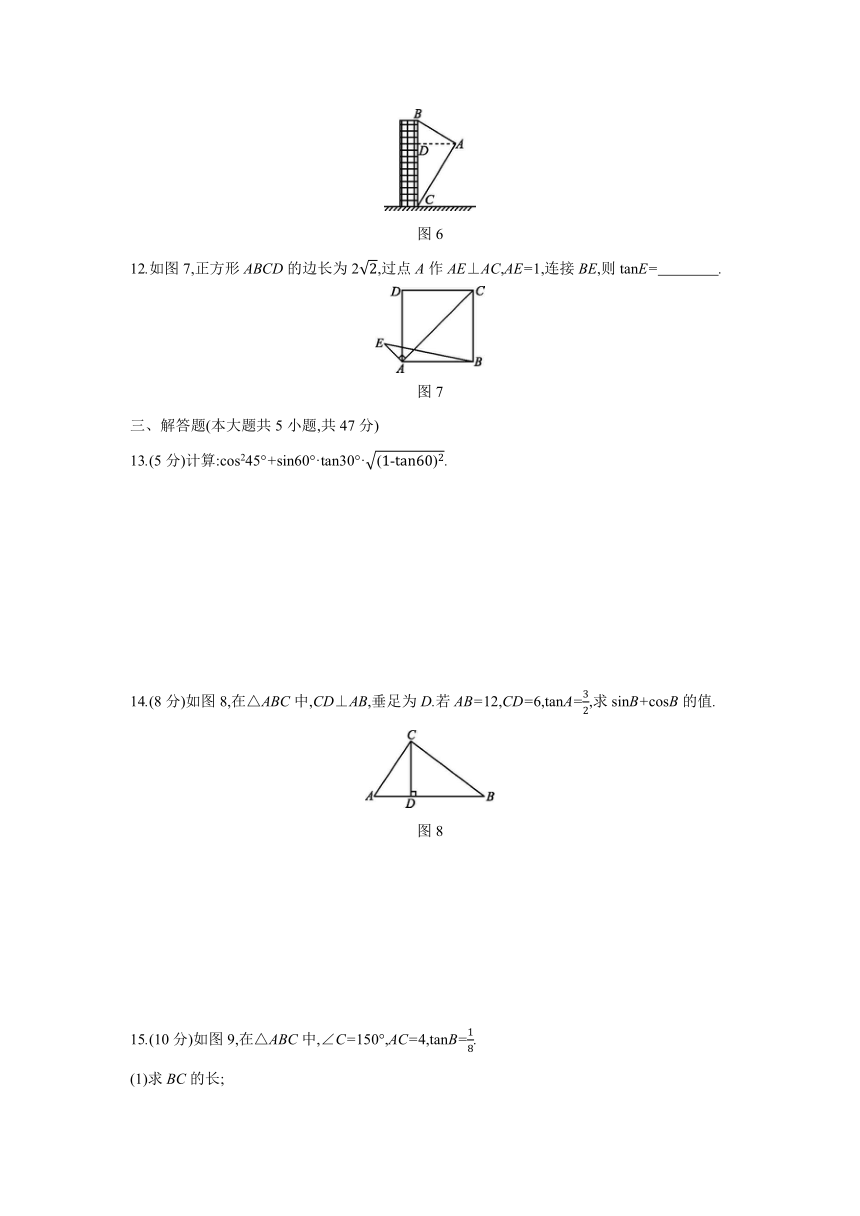
11.如图6,航拍无人机从A处测得一幢建筑物顶部B的仰角为30°,测得底部C的俯角为60°,此时航拍无人机与该建筑物的水平距离AD为90米,那么该建筑物的高度BC约为
米.(精确到1米,参考数据:≈1.73)?
图6
12.如图7,正方形ABCD的边长为2,过点A作AE⊥AC,AE=1,连接BE,则tanE= .?
图7
三、解答题(本大题共5小题,共47分)
13.(5分)计算:cos245°+sin60°·tan30°·.
14.(8分)如图8,在△ABC中,CD⊥AB,垂足为D.若AB=12,CD=6,tanA=,求sinB+cosB的值.
图8
15.(10分)如图9,在△ABC中,∠C=150°,AC=4,tanB=.
(1)求BC的长;
(2)利用此图形求tan15°的值(结果精确到0.1,参考数据:≈1.41,≈1.73).
图9
16.(12分)天门索道是世界最长的高山客运索道,位于张家界天门山景区.在一次检修维护中,检修人员从索道A处开始,沿A-B-C路线对索道进行检修维护,如图10所示,已知AB=500米,BC=800米,AB与水平线AA1的夹角是30°,BC与水平线BB1的夹角是60°.求:本次检修中,检修人员上升的垂直高度CA1是多少米.(结果精确到1米,参考数据:≈1.732)
图10
17.(12分)如图11,广安市防洪指挥部发现渠江边一处长400米,高8米,背水坡的坡角为45°的防洪大堤(横截面为梯形ABCD)急需加固.经调查论证,防洪指挥部专家组制定的加固方案是:背水坡面用土石进行加固,并使上底加宽2米,加固后,背水坡EF的坡比i=1∶2.
(1)求加固后坝底增加的宽度AF的长;
(2)完成这项工程需要土石多少立方米?
图11
答案
1.A
2.[解析]
A ∵AC=2
m,坡角为30°,∴cos30°=,∴=,解得AB=4(m).故选A.
3.[解析]
D 锐角的正弦值与它的余角的余弦值相等;锐角的余弦值与它的余角的正弦值相等.
4.[解析]
A 由题意可知A(-1,0),B(0,2),∴OA=1,OB=2,AB=,则sin∠BAO=,tan∠BAO=2,tan∠ABO=,
cos∠ABO=.
5.[解析]
C 连接AC.易知AB2=AC2=10,BC2=20,则AB2+AC2=BC2,故△ABC是等腰直角三角形,∴sin∠ABC=sin45°=.
6.[解析]
B 调整前梯子顶端到地面的距离为4×sin45°=2(m),调整后梯子顶端到地面的距离为4×sin60°=2(m),所以梯子的顶端沿墙面升高的距离为2()m.
7.[解析]
B 如图,过点A作AE⊥BD,交DB的延长线于点E,则AE∥CD,
∴∠DAE=∠ADC.
由题意可得∠ABE=180°-90°-45°=45°.
设AE=1,则BE=1,AB=,
∴BC=.
又∵△BCD是等腰直角三角形,
∴BD=,∴DE=1+,
∴tan∠ADC=tan∠DAE==+1.
8.[答案]
35°
[解析]
∵tan(α+10°)=1,
∴α+10°=45°,∴α=35°.
9.[答案]
[解析]
根据题意可知tanα=1,则α=45°,故原式=sin60°+cos30°=+=.
10.[答案]
30°
[解析]
设这个等腰三角形底角的度数为α,则cosα=,故α=30°.
11.208
12.[答案]
[解析]
如图,设BE与AC相交于点F,连接BD,交AC于点O.
在正方形ABCD中,∠BOA=90°.∵AE⊥AC,
∴AE∥BD,
∴△AEF∽△OBF,∴=.
∵正方形ABCD的边长为2,
∴OA=OB=2.
∵AE=1,∴==.
又∵AF+OF=OA=2,
∴AF=,∴tanE===.
13.解:原式=()2+
=+×(-1)
=.
14.解:在Rt△ACD中,∵CD=6,
tanA==,
∴AD=4,∴BD=AB-AD=8.
在Rt△BCD中,BC==10,
∴sinB==,cosB==,
∴sinB+cosB=.
15.解:(1)过点A作AD⊥BC,交BC的延长线于点D,如图所示.
在Rt△ADC中,AC=4,
∵∠ACB=150°,∴∠ACD=30°,
∴AD=AC=2,CD=AC·cos30°=4×=2.
在Rt△ABD中,
∵tanB===,
∴BD=16,
∴BC=BD-CD=16-2.
(2)在BC边上取一点M,使得CM=AC,
连接AM,如图所示.
∵∠ACB=150°,
∴∠AMC=∠MAC=15°,
∴tan15°=tan∠AMC====2-≈0.3.
16.解:如图,过点B作BH⊥AA1于点H,则四边形BB1A1H为矩形,∴A1B1=BH.
∵在Rt△ABH中,AB=500米,∠BAH=30°,
∴BH=AB=×500=250(米),
∴A1B1=BH=250
米.
∵在Rt△BB1C中,BC=800米,∠CBB1=60°,
∴B1C=BC·sin∠CBB1=800×=400(米),
∴检修人员上升的垂直高度CA1=B1C+A1B1=400+250≈943(米).
答:本次检修中,检修人员上升的垂直高度CA1约是943米.
17.解:(1)如图,分别过点D,E作DH⊥AB,EG⊥AB,交AB于点H,G,
则四边形EGHD是矩形,
∴GH=ED=2米.
由题意,得EG=DH=8米.
在Rt△ADH中,
AH===8(米).
∵在Rt△FGE中,i=1∶2=EG∶FG,
∴FG=2EG=16
米,
∴AF=FG+GH-AH=16+2-8=10(米).
答:加固后坝底增加的宽度AF的长为10米.
(2)加宽部分的体积V=S梯形AFED×坝长=×(2+10)×8×400=19200(米3).
答:完成这项工程需要土石19200立方米.
一、选择题(本大题共7小题,每小题4分,共28分)
1.已知:在Rt△ABC中,∠C=90°,BC=3,AC=4,则tanB的值是
( )
A.
B.
C.
D.
2.如图1,坡角为30°的斜坡上两树间的水平距离AC为2
m,则两树间的坡面距离AB为
( )
图1
A.4
m
B.
m
C.
m
D.4
m
3.当∠A,∠B为锐角,且∠A+∠B=90°时,下列结论错误的是
( )
A.cosA=sinB
B.sinA=cosB
C.sinA=cos(90°-∠A)
D.sin(90°-∠A)=sinA
4.如图2所示,一次函数y=2x+2的图象与x轴交于点A,与y轴交于点B,则下列结论正确的是
( )
图2
A.sin∠BAO=
B.tan∠BAO=
C.tan∠ABO=-
D.cos∠ABO=
5.如图3所示,每个小正方形的边长均为1,A,B,C均为小正方形的顶点,则∠ABC的正弦值为
( )
图3
A.1
B.
C.
D.
6.长为4
m的梯子搭在墙上与地面成45°角,作业时调整成60°角,如图4所示,则梯子的顶端沿墙面升高的距离为
( )
图4
A.(2-)m
B.2(-)m
C.(2-)m
D.2(+)m
7.将一副三角尺如图5①摆放在一起,示意图如图②,连接AD,则∠ADC的正切值为( )
图5
A.-1
B.+1
C.2
D.3
二、填空题(本大题共5小题,每小题5分,共25分)
8.若tan(α+10°)=1,则锐角α的度数是 .?
9.已知α为锐角,当无意义时,sin(α+15°)+cos(α-15°)的值为 .?
10.如果一个等腰三角形的三条边长分别为1,1,,那么这个等腰三角形底角的度数为 .?
11.如图6,航拍无人机从A处测得一幢建筑物顶部B的仰角为30°,测得底部C的俯角为60°,此时航拍无人机与该建筑物的水平距离AD为90米,那么该建筑物的高度BC约为
米.(精确到1米,参考数据:≈1.73)?
图6
12.如图7,正方形ABCD的边长为2,过点A作AE⊥AC,AE=1,连接BE,则tanE= .?
图7
三、解答题(本大题共5小题,共47分)
13.(5分)计算:cos245°+sin60°·tan30°·.
14.(8分)如图8,在△ABC中,CD⊥AB,垂足为D.若AB=12,CD=6,tanA=,求sinB+cosB的值.
图8
15.(10分)如图9,在△ABC中,∠C=150°,AC=4,tanB=.
(1)求BC的长;
(2)利用此图形求tan15°的值(结果精确到0.1,参考数据:≈1.41,≈1.73).
图9
16.(12分)天门索道是世界最长的高山客运索道,位于张家界天门山景区.在一次检修维护中,检修人员从索道A处开始,沿A-B-C路线对索道进行检修维护,如图10所示,已知AB=500米,BC=800米,AB与水平线AA1的夹角是30°,BC与水平线BB1的夹角是60°.求:本次检修中,检修人员上升的垂直高度CA1是多少米.(结果精确到1米,参考数据:≈1.732)
图10
17.(12分)如图11,广安市防洪指挥部发现渠江边一处长400米,高8米,背水坡的坡角为45°的防洪大堤(横截面为梯形ABCD)急需加固.经调查论证,防洪指挥部专家组制定的加固方案是:背水坡面用土石进行加固,并使上底加宽2米,加固后,背水坡EF的坡比i=1∶2.
(1)求加固后坝底增加的宽度AF的长;
(2)完成这项工程需要土石多少立方米?
图11
答案
1.A
2.[解析]
A ∵AC=2
m,坡角为30°,∴cos30°=,∴=,解得AB=4(m).故选A.
3.[解析]
D 锐角的正弦值与它的余角的余弦值相等;锐角的余弦值与它的余角的正弦值相等.
4.[解析]
A 由题意可知A(-1,0),B(0,2),∴OA=1,OB=2,AB=,则sin∠BAO=,tan∠BAO=2,tan∠ABO=,
cos∠ABO=.
5.[解析]
C 连接AC.易知AB2=AC2=10,BC2=20,则AB2+AC2=BC2,故△ABC是等腰直角三角形,∴sin∠ABC=sin45°=.
6.[解析]
B 调整前梯子顶端到地面的距离为4×sin45°=2(m),调整后梯子顶端到地面的距离为4×sin60°=2(m),所以梯子的顶端沿墙面升高的距离为2()m.
7.[解析]
B 如图,过点A作AE⊥BD,交DB的延长线于点E,则AE∥CD,
∴∠DAE=∠ADC.
由题意可得∠ABE=180°-90°-45°=45°.
设AE=1,则BE=1,AB=,
∴BC=.
又∵△BCD是等腰直角三角形,
∴BD=,∴DE=1+,
∴tan∠ADC=tan∠DAE==+1.
8.[答案]
35°
[解析]
∵tan(α+10°)=1,
∴α+10°=45°,∴α=35°.
9.[答案]
[解析]
根据题意可知tanα=1,则α=45°,故原式=sin60°+cos30°=+=.
10.[答案]
30°
[解析]
设这个等腰三角形底角的度数为α,则cosα=,故α=30°.
11.208
12.[答案]
[解析]
如图,设BE与AC相交于点F,连接BD,交AC于点O.
在正方形ABCD中,∠BOA=90°.∵AE⊥AC,
∴AE∥BD,
∴△AEF∽△OBF,∴=.
∵正方形ABCD的边长为2,
∴OA=OB=2.
∵AE=1,∴==.
又∵AF+OF=OA=2,
∴AF=,∴tanE===.
13.解:原式=()2+
=+×(-1)
=.
14.解:在Rt△ACD中,∵CD=6,
tanA==,
∴AD=4,∴BD=AB-AD=8.
在Rt△BCD中,BC==10,
∴sinB==,cosB==,
∴sinB+cosB=.
15.解:(1)过点A作AD⊥BC,交BC的延长线于点D,如图所示.
在Rt△ADC中,AC=4,
∵∠ACB=150°,∴∠ACD=30°,
∴AD=AC=2,CD=AC·cos30°=4×=2.
在Rt△ABD中,
∵tanB===,
∴BD=16,
∴BC=BD-CD=16-2.
(2)在BC边上取一点M,使得CM=AC,
连接AM,如图所示.
∵∠ACB=150°,
∴∠AMC=∠MAC=15°,
∴tan15°=tan∠AMC====2-≈0.3.
16.解:如图,过点B作BH⊥AA1于点H,则四边形BB1A1H为矩形,∴A1B1=BH.
∵在Rt△ABH中,AB=500米,∠BAH=30°,
∴BH=AB=×500=250(米),
∴A1B1=BH=250
米.
∵在Rt△BB1C中,BC=800米,∠CBB1=60°,
∴B1C=BC·sin∠CBB1=800×=400(米),
∴检修人员上升的垂直高度CA1=B1C+A1B1=400+250≈943(米).
答:本次检修中,检修人员上升的垂直高度CA1约是943米.
17.解:(1)如图,分别过点D,E作DH⊥AB,EG⊥AB,交AB于点H,G,
则四边形EGHD是矩形,
∴GH=ED=2米.
由题意,得EG=DH=8米.
在Rt△ADH中,
AH===8(米).
∵在Rt△FGE中,i=1∶2=EG∶FG,
∴FG=2EG=16
米,
∴AF=FG+GH-AH=16+2-8=10(米).
答:加固后坝底增加的宽度AF的长为10米.
(2)加宽部分的体积V=S梯形AFED×坝长=×(2+10)×8×400=19200(米3).
答:完成这项工程需要土石19200立方米.
